¿Periferia, superficie e irracional?
¿Periferia, superficie e irracional?
Aprendizaje esperado: calcula el perímetro de polígonos y del círculo, y áreas de triángulos y cuadriláteros, desarrollando y aplicando fórmulas.
Énfasis: analizar la construcción de las fórmulas del perímetro y área del círculo.
¿Qué vamos a aprender?
El propósito de esta lección es que analices la construcción de las fórmulas del perímetro del círculo, de tal manera que puedas observar la relación que existe entre dicha fórmula y su asociación con el número irracional pi.
¿Qué hacemos?
Los círculos son figuras planas y cerradas, pero no forman parte de los polígonos, ya que el círculo se encuentra formado por un infinito número de lados, los cuales forman una curva cerrada.
Esta figura es muy común en la vida diaria, ya que la puedes observar en objetos que utilizas normalmente. Por ejemplo, en las ruedas de una bicicleta, la base de los cilindros donde tomas agua o incluso en tu cuerpo, en el iris de tus ojos.
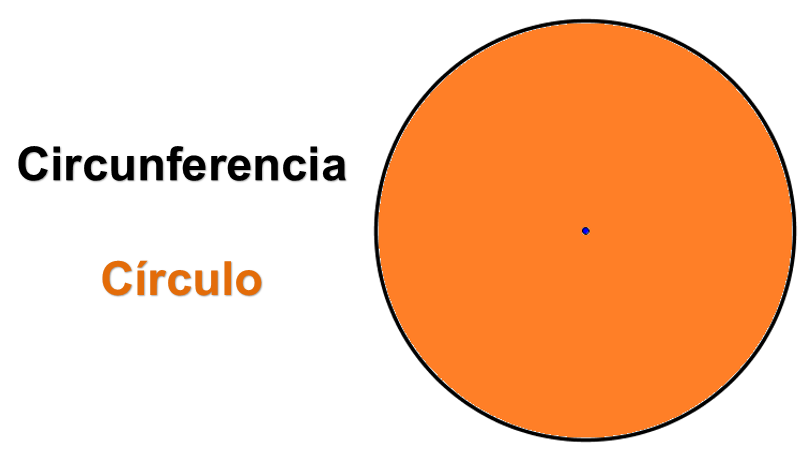
Es importante establecer la diferencia que existe entre circunferencia y círculo. Se podría definir la circunferencia como:
- Aquella figura generada por una curva cerrada
- Sin vértices ni ángulos
- Es bidimensional
- Y tiene un radio que es la distancia (siempre la misma) que hay entre cada punto de la curva cerrada y el centro de la misma.
Generalmente, a la circunferencia se le confunde con el círculo, que en realidad es el área delimitada por la circunferencia; en todo caso, la circunferencia podría ser el perímetro del círculo. Existen líneas notables en las circunferencias, pero en esta sesión utilizarás sólo dos: el diámetro y el radio.
Podemos definir el radio como un segmento de recta que une el centro de la circunferencia con un punto cualquiera de la circunferencia. La circunferencia tiene un número infinito de radios.
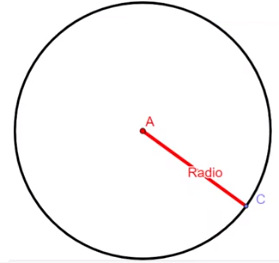
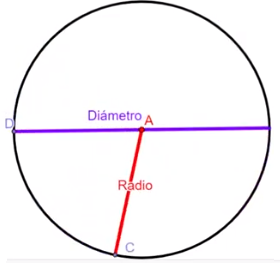
El diámetro se define como un segmento de recta que une dos puntos de la circunferencia pasando por el centro del círculo; cabe mencionar que el diámetro es el doble de la longitud del radio. Para determinar las longitudes de la circunferencia y el diámetro, utilizaremos estos tres objetos.
Te invitamos a que busques en tu hogar tres objetos en donde observes un círculo, y a que tomes las medidas de la circunferencia y del diámetro. Registra las medidas de la circunferencia y su diámetro para determinar qué relación existe entre éstas. Elabora una tabla con la siguiente información: en la primera columna registramos el objeto, como ejemplo en este caso utilizaremos la base de un cilindro para agua, un disco de acetato y un hula hula; en la segunda columna, la longitud en centímetros de la circunferencia, en la tercera columna, la longitud en centímetros de el diámetro, en la cuarta columna se encuentra la relación entre la longitud de la circunferencia y la longitud del diámetro, expresada como la razón circunferencia sobre diámetro. Los resultados para estos objetos fueron los siguientes:
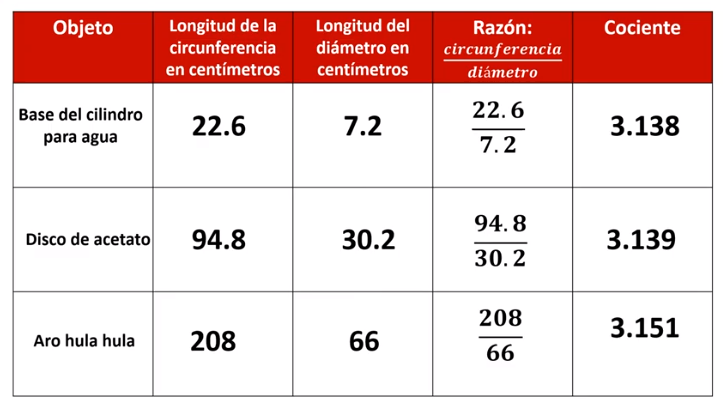
Observa que los cocientes de las relaciones que existen entre las longitudes de las circunferencias y la longitud de sus diámetros son 3.138, 3.139 y 3.151; estos números tienen algo en común. Su valor se aproxima a una constante que representa a un número importante que queremos destacar. Es “pi”, el cual tiene un valor aproximado de 3.1416, para saber cómo llegamos a esta medida, observa el siguiente video:
- Demostración de Pi
Autor: Víctor J. Barabata Villasana
https://youtu.be/daPR3_Ndn_I
Pi es también un número irracional, lo que quiere decir que no se puede expresar como una fracción exacta; veintidós séptimos se acerca más al valor de pi, pero no es pi en realidad.
Varios matemáticos famosos han intentado calcular con mayor precisión el valor de pi; por ejemplo, Arquímedes, él utilizó un método bastante ingenioso en el que trazaba polígonos inscritos en una circunferencia como el que se muestra en la imagen de la Luna, donde se relaciona el perímetro del polígono interior y el diámetro de la imagen, y también trazaba polígonos circunscritos, como se aprecia en el polígono exterior en la imagen del Sol. son sólo imágenes, ya que sabemos que la Luna y el Sol no son objetos circulares y no tienen una circunferencia trazada que los delimite.
Al incrementar el número de lados en los polígonos, los valores de pi cambian, acercándose más a su valor. En relación con los perímetros de los polígonos, Arquímedes dedujo que el valor de pi estaba, muy cercano, entre 3.1410 y 3.1427, relacionando polígonos de hasta 96 lados.
Posteriormente, Zu Chongzhi se aproximó más al valor de pi usando un polígono de 12 288 lados, con un resultado más preciso entre 3.14926 y 3.1415927. Durante muchos siglos estas aproximaciones han sido muy útiles para los seres humanos. Pero esto no ha sido suficiente, ya que varios matemáticos en diferentes épocas a lo largo de la historia continuaron calculando más y más dígitos decimales para pi.
Algunos ejemplos de estos cálculos son los siguientes: en India, Madhava de Sangamagrama inventó el método llamado método de las series infinitas; más adelante, y ayudado de este método, Abraham Sharp pudo calcular 76 dígitos de pi; Daniel Ferguson, en 1946, calculó 620 cifras decimales; todo esto, incluso, antes del uso de las calculadoras. En la época actual, con apoyo de las computadoras y nuevos algoritmos, han logrado darle el valor a pi de 3.141592 y millones y millones de cifras decimales más. Una característica fundamental de estos decimales es que no siguen un patrón y ningún dígito aparece con más frecuencia que otro.
Conocer la historia ayuda a entender mejor el porqué de los procedimientos. Ahora resolvamos la siguiente situación: a un carpintero le encargaron hacer una mesa circular que mide 0.7 metros de radio. Si desea poner un borde metálico dorado, ¿cuál es la longitud del borde que utilizará la mesa?
El borde metálico que lleva la mesa representa la circunferencia, pero ¿cómo calculamos la longitud de la circunferencia? Para conocer la respuesta, observa el siguiente video. - Deducción de la longitud de una circunferencia
Autor: Víctor Jesús Barabata Villasana
https://youtu.be/rY50zfIxJWE
Como ya tienes la fórmula para calcular la longitud de una circunferencia, demos solución a la situación.
A un carpintero le encargaron hacer una mesa circular que mide 0.7 metros de radio. Si desea poner un borde metálico dorado, ¿cuál es la longitud del borde que utilizará la mesa? En la imagen puedes observar el borde metálico y el radio de la circunferencia, que es 0.7 m.
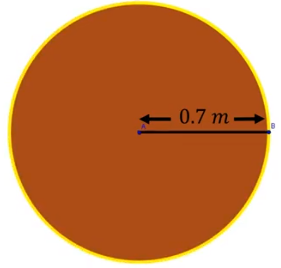
La situación pide que calcular la longitud del borde metálico que se colocará en la mesa, que estaría representando la circunferencia, es decir, el contorno. La fórmula para calcular la circunferencia es:
C = 2r π
Donde C es la circunferencia, r es el radio, así que determinemos nuestros datos: r = .7m, para π (Pi) utilizaremos el valor aproximado que es 3.1416.
Sustituyendo los valores numéricos en ella. Resulta:

Por lo tanto, la longitud del borde metálico es de 4.3982 metros.
¿Te has subido al juego mecánico del carrusel?, ¿has percibió que se recorre una menor distancia cuando se está sentado en una figura más cercana al centro?
Si en un carrusel el primer caballo se encuentra a 3 metros del centro y el segundo caballo se encuentra a 4.5 metros, ¿qué distancia recorren en una vuelta cada uno de los caballos?
En la siguiente imagen puedes observar dos figuras, y la distancia de la primera figura al centro del carrusel representa el radio de la circunferencia, que es 3 m, y la segunda figura está ubicada a una distancia de 4.5 metros, por lo tanto, esa es la medida del otro radio.
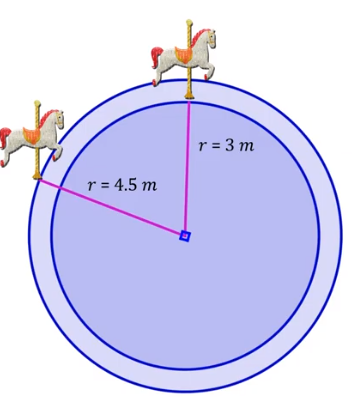
La situación pide que calcular la longitud de una vuelta de cada una de las figuras, que estarían representando la circunferencia, es decir, la distancia que recorrerán en el primer giro del carrusel. Comencemos a calcular la longitud de la circunferencia de la primera figura. La fórmula para calcular la longitud de la circunferencia es C = 2r π, así que determinemos nuestros datos:

Sustituyendo los valores numéricos en ella. Resulta:

Por lo tanto, la longitud de una vuelta que recorre el primer caballo es de 18.8496 metros.
Ahora calculemos la longitud de la vuelta que recorre el segundo caballo.
Determinemos los datos:
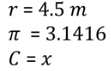
Sustituyendo los valores numéricos en ella. Resulta:

Por lo tanto, la longitud de una vuelta que recorre el segundo caballo es de 28.2744 metros.
Recapitulando lo estudiado en esta lección. Podríamos decir que la circunferencia es aquella figura generada por una curva cerrada, y tiene un radio que es la distancia (siempre la misma) que hay entre cada punto de la curva cerrada y el centro de la misma; mientras que el círculo es el área delimitada por la circunferencia. Es importante no confundirlos. No olvides que la longitud de la circunferencia se calcula de la siguiente manera: 2 veces el radio por pi, o lo que es igual, pi por diámetro.
Toma en cuenta que el número pi es un número irracional, cuyo valor exacto no se conoce, así que, por convencionalidad, se utiliza su valor aproximado, que es 3.1416.
El reto de hoy:
Como reto, ahora te proponemos calcular la longitud de la circunferencia de los siguientes círculos.
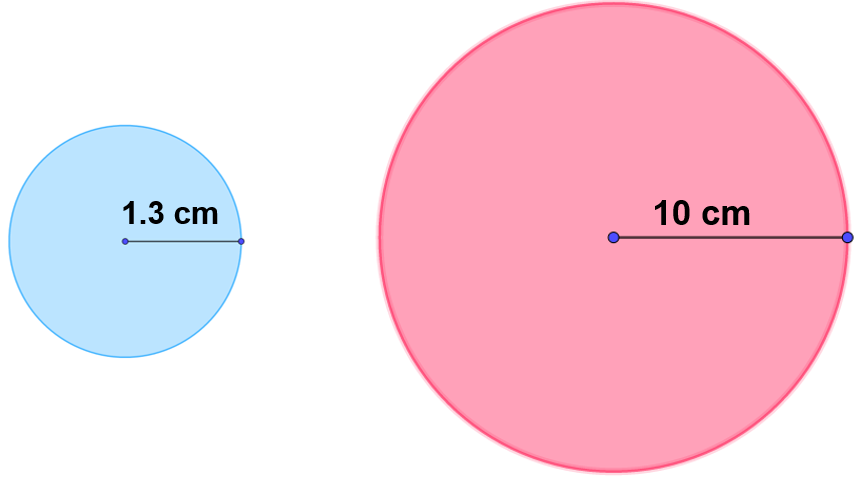
En la imagen puedes observar dos círculos: el primero, de color azul, con un radio de 1.3 centímetros, y el segundo, en color rojo, cuyo radio mide 10 centímetros de longitud. Toma en cuenta que utilizarás el valor aproximado de pi, que es 3.1416.
¡Buen trabajo!
Gracias por tu esfuerzo.