Tanto por ciento
Tanto por ciento
Aprendizaje esperado: resuelve problemas de cálculo de porcentajes, de tanto por ciento y de la cantidad base.
Énfasis: identificar diferentes maneras de representar un porcentaje. Calcular porcentajes de una cantidad dada.
¿Qué vamos a aprender?
En esta sesión ampliarás tus conocimientos sobre el tema “Tanto por ciento y sus diferentes representaciones”, para lograrlo realizarás algunas actividades que te auxiliarán a precisar algunas peculiaridades sobre este interesante tema.
Toma nota de cada una de las actividades que se desarrollarás. Pon mucha atención, ya que comenzarás con otra aventura llena de conocimientos.
Para lograr un mejor desempeño en tus actividades y tomar nota de lo que se presente, te recomiendo tener siempre cerca de ti:
- Su cuaderno, o bien, hojas reutilizables
- Lápiz
- Goma
- Y tu libro de texto de la asignatura de Matemáticas
¿Qué hacemos?
En sesiones anteriores aprendiste a calcular el porcentaje de una cantidad base y a representar el tanto por ciento como fracción y decimal. En esta sesión, además de calcularlo, fortalecerás el significado de este concepto y estudiarás las diferentes formas en que un porcentaje se puede representar: como fracción, como número decimal o utilizando su símbolo, que es: %. Harás el cálculo del mismo a partir de una cantidad dada.
El porcentaje se utiliza en diferentes ámbitos de la vida cotidiana, por ejemplo, cuando vas al supermercado y algunos productos ofrecen un descuento en su compra, en una tienda departamental, en la política, en fenómenos estadísticos, en la escuela y en muchas situaciones más. Por esto es importante su estudio y comprensión para poder aplicarlo en diferentes contextos.
El uso del porcentaje es muy común en distintas situaciones de la vida diaria, porque permite conocer la relación entre una cantidad y un total. Al dividir un total (100 %) en 100 partes iguales, es más práctico hablar de las partes que lo componen.
Para esto considera qué es el porcentaje y cómo puedes representarlo.
El porcentaje es la cantidad que, de manera proporcional hace referencia a una parte del todo. La representación de los porcentajes consiste en un número acompañado del símbolo %, que se lee “por ciento” y se traduce como “una parte de cada cien”; por ejemplo, 35 % representa 35 de cada 100, por lo que también puede expresarse como 35/100 y simplificando la fracción puedes encontrar el número decimal que represente a la misma, así se tiene que 35/100 es igual a 7/20 resolviendo la división que representa la fracción 7 entre 20 es igual a 0.35.
Una posible representación gráfica de lo anterior es:

Están sombreadas 35 de cada 100 partes de la superficie de la figura.
Están sombreados 35/100 o 7/20 de cuadrados de la figura.
Están sombreados 0.35 partes de la superficie de la figura.
Y usando porcentajes, todo lo anterior es igual a…
Está sombreado 35 % de la figura.
De acuerdo con lo anterior, es posible representar un porcentaje como un número fraccionario y como un número decimal.
Observa algunos ejemplos organizados en la siguiente tabla. Toma nota, por favor.
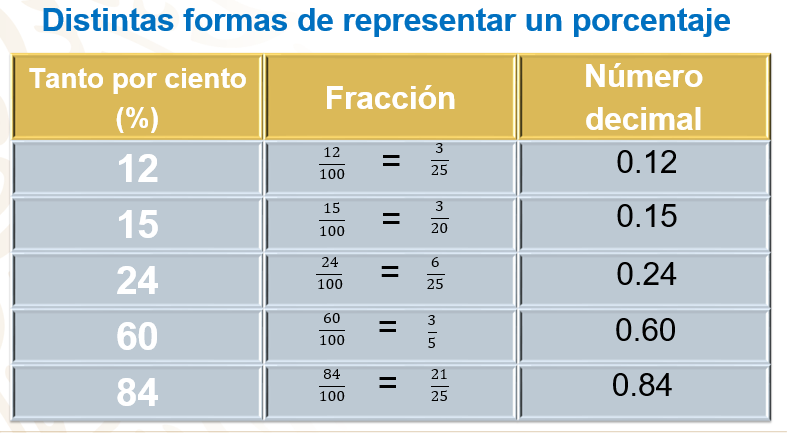
La tabla está formada por tres columnas: en la primera columna se tienen algunos porcentajes dados en tanto por ciento y se escribe el porcentaje utilizando su símbolo correspondiente; en la segunda columna se escribe el porcentaje en su forma de fracción decimal y en su forma simplifica y en la tercera columna se anota en forma decimal a cada uno de los porcentajes dados.
En primer lugar, se tiene 12 por ciento que representa 12 de cada 100, que en fracción decimal se escribe 12/100, simplificando nos da 3/25, resolviendo la división que representa la fracción 3/25, tenemos 3 entre 25 y se obtiene el número decimal 0.12.
Después se tiene el 15 por ciento, que representa 15 de cada 100 y en su forma fraccionaria se escribe 15/100, simplificando la fracción se obtiene 3/20, que como número decimal es equivalente a 0.15.
En tercer lugar, se tiene el 24 por ciento que representa 24 de cada 100, en fracción decimal se escribe como 25/100, simplificando la fracción nos da 6/25, que es equivalente a 0.24.
Para la cuarta fila se tiene 60 por ciento.
Seguramente en casa ya sabes cómo representar este porcentaje como fracción y como número decimal. Observa.
60 por ciento, que representa 60 de cada 100, se escribe como fracción decimal 60/100, simplificando la fracción se obtiene 3/5, que equivale a 0.60.
En quinto lugar, está 84 por ciento, que representa 84 de cada 100, como fracción decimal se escribe 84/100, simplificando la fracción tenemos 21/25, al resolver la división se obtiene el número decimal 0.84.
Como pudiste observar en la tabla anterior, el porcentaje o tanto por ciento se puede representar con un número fraccionario con denominador 100 o como un número decimal.
Cuando se aplica el tanto por ciento a una cantidad, se relacionan tres cantidades:
El tanto por ciento (tasa); la cantidad inicial a la que se aplica el tanto por ciento (cantidad base) y el porcentaje, que es la cantidad final.
Ahora reflexiona con algunos casos en donde es necesario calcular el tanto por ciento y qué procedimiento vas a utilizar para poder obtener el porcentaje de una cantidad dada.
El porcentaje de una cantidad se obtiene estableciendo la siguiente relación entre los datos.
Porcentaje o cantidad final = cantidad inicial (base) por tanto por ciento en su forma decimal, por ejemplo:
Se tiene el 35 por ciento de 1200. La cantidad inicial es 1 200, el tanto por ciento es 35. Se representa el 35 % como fracción o como número decimal:
Así se obtiene que 35 % = 35/100=7/20 = 0.35.
Para obtener el porcentaje se realizan las siguientes operaciones 35/100 por 1200 = 42 000/100 = 420
O bien, representando el 35 por ciento como número decimal tendremos 1 200 por 0.35 = 420
Observa algunos porcentajes que son equivalentes a fracciones comunes conocidas, lo que facilita su cálculo. En los siguientes ejemplos, la equivalencia se indica con una flecha.
Considera esta información, te puede resultar muy útil para realizar cálculos de porcentajes de manera más rápida.

Cincuenta por ciento corresponde a la mitad de un todo.
Cincuenta por ciento es equivalente a 50 sobre 100, que se puede simplificar a un medio y expresado a su forma decimal corresponde a 0.50.
Veinticinco por ciento es la cuarta parte de un todo, es equivalente a veinticinco sobre 100 que se puede simplificar a un cuarto, un cuarto convertido a decimal es igual a 25 centésimos.
75 por ciento es tres cuartos de un todo, y equivale a la fracción 75 sobre 100 y esta es equivalente a ¾, convirtiendo la fracción a número decimal tenemos 0.75.
10 porciento es la décima parte de un todo. El 10 % es equivalente a 10/100 y esta fracción es equivalente a 1/10, convirtiendo la fracción a número decimal tenemos 0.10.
20 por ciento es la quinta parte de un todo; equivale a una quinta parte y convirtiéndolo a decimal es igual a veinte séptimos.
El 5 por ciento es la vigésima parte de un todo; equivale 5/100 y se simplifica a 1/20 convirtiendo la fracción a decimal obtenemos 0.05.
Reflexiona con la siguiente situación y analiza los comportamientos que se van presentando dada una relación de magnitudes vista.
Prepara bolsas de globos, de modo que, de cada 25 globos que se echen en una bolsa, 5 son de color rojo, lo cual se puede representar como 5/25.
Considerando esa razón, entonces en dos bolsas habría 50 globos, de los cuales 10 son de color rojo, lo cual se representa por la fracción 10/50.
Ahora, si consideramos tres bolsas, hay 75 globos, de los cuales 15 serán de color rojo, que representa 15/75.
Entonces, en cuatro bolsas habría 100 globos, de los cuales 20 son de color rojo, lo que representa 20/100.
En lugar de “20 de cada 100”, se dice 20 por ciento y se escribe 20 %.
Observa cómo las razones obtenidas son equivalentes; por lo tanto, en cada caso, el número de globos rojos representa 20 % del total de globos.
Ahora observa otra situación en donde es necesario calcular el aumento porcentual de una cantidad. Analiza y reflexiona sobre los pasos que son necesarios seguir para determinar de manera correcta el resultado.
El aumento porcentual son problemas en los que algo tiene un valor inicial, aumenta en un porcentaje de su valor y llega a un valor final.
Por ejemplo:
En cierta ocasión a Verónica le ofrecieron en su trabajo un aumento de 15 % en su salario mensual base, el cual era de $11 000.00, entonces me pidió que si le podía ayudar a determinar cuánto dinero le iban a aumentar.
¿Ya sabes cómo ayudar a Verónica?
Revisa la situación, y resuelve conjuntamente esta situación y verifica al final si los cálculos y resultados obtenidos fueron los correctos.
Se tienen los siguientes datos:
Sueldo base $ 11 000
Aumento salarial 15 %
Las operaciones para saber cuánto dinero le aumentaron a Verónica son:
15 % = 15/100 = 3/20 = 0.15
Y para calcular 15 por ciento de $11 000 multiplicamos 11 000 por 0.15, que es igual a 1 650.
Ya se sabe que 1 650 es el 15 % de 11 000. Les pregunto, ¿cuál será el nuevo salario de Verónica?
Suma su sueldo base más la cantidad que le aumentarán: 11 000 + 1 650 = 12 650
El salario de Verónica será de $12 650.
Se espera que la situación anterior te haya permitido comprender la estrategia para poder calcular aumentos porcentuales en diferentes contextos.
Ahora se detallará una situación que te ayudará a resolver con base en los conocimientos que ya has adquirido, reflexiona con la siguiente situación-problema, que se refieren a disminución porcentual.
Las situaciones referidas a disminución porcentual son aquellas en las que algo tiene un valor inicial, disminuye en un porcentaje de su valor y llega a un valor final,
como la que se presenta a continuación.

La imagen muestra el folleto de la tienda de ropa “Don Fernando”, en la que se muestran algunas promociones de descuento en la ropa.
Kinerette está interesada en comprar algunas prendas de las que aparecen en el folleto.
Ayuda a Kinerette a saber cuánto pagará por los artículos seleccionados con el descuento.
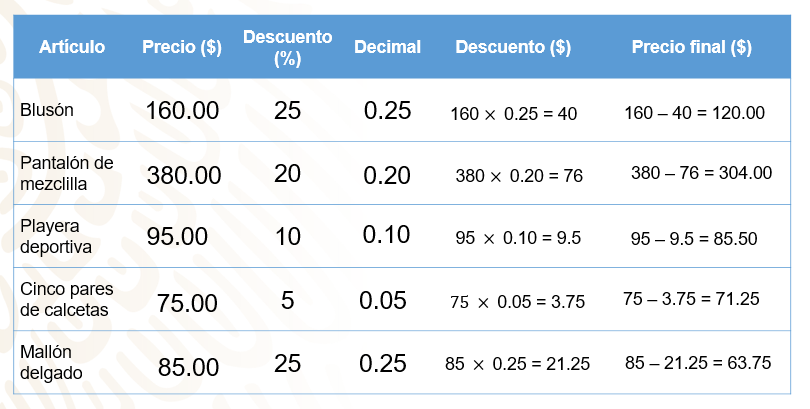
Analiza la tabla que muestra el precio de los artículos que quiere comprar Kinerette.
¿Cuánto se le descontó por cada artículo?, ¿Cuánto pago por cada uno?, ¿Cuánto pagó en total?, ¿Cuánto dinero ahorro con su compra Kinerette?
En la primera columna se encuentra el artículo en venta, en la segunda columna se tiene el precio por artículo, en la tercera columna se tiene el descuento en porcentaje, en la cuarta columna se tiene el porcentaje de descuento como número decimal, en la quinta columna se tiene el descuento representado en pesos y en la última columna se tiene el precio final ya con descuento.
Comienza con el blusón, su precio es de 160 pesos, con un descuento de 25 %, que es igual a 25/100 y como número decimal es igual a 0.25.
Para saber el precio final del blusón, multiplica el precio original por el porcentaje de descuento como número decimal, esto es: 160 por 0.25, que es igual a 40 pesos. Después, resta al precio original el descuento para obtener el precio final, 160 menos 40 es igual a 120, es decir, que el precio final con descuento del blusón es igual a 120 pesos.
Continúa con el pantalón de mezclilla: precio de 380 pesos con descuento de 20 por ciento que como número decimal es igual a 0.20. Ahora calcula el descuento en pesos, para esto multiplica 380 pesos por 0.20 que representa el tanto por ciento en su forma decimal, el resultado es igual a 76 pesos, lo que representa un descuento de 76 pesos; para tener el precio final se restan 380 menos 76, que es igual a 304 pesos.
El siguiente artículo es la playera deportiva con un precio inicial de 95 pesos, un descuento del 10 por ciento, que es igual a 0.10; el descuento en pesos equivale a multiplicar 95 por 0.10, que es igual a 9.5 pesos, para tener el precio final resta 95 menos 9.5, que es igual a 85 pesos con cincuenta centavos.
Continúa con los 5 pares de calcetas. En este caso, el costo de un sólo par de calcetas es igual a 15 pesos, pero como se tienen cinco piezas del mismo artículo multiplica el precio de un par de calcetas por 5, ahora si ya tienes el precio de los 5 artículos, que es de 75 pesos, los cuales tienen un descuento de 5 %, que es igual a 0.05, ahora calcula el descuento multiplicando el precio inicial por el decimal 75 por 0.05, que es igual a 3.75. Ahora para calcular el precio final realiza la resta 75 menos 3.75 es igual a 71.25 pesos.
Termina tus cálculos con el mallón delgado que tiene un precio inicial de 85 pesos y un descuento del 25 por ciento que como número decimal es igual a 0.25; ya puedes calcular el descuento en pesos multiplicando 85 pesos por 0.25, que es igual a 21.25.
Por último, para obtener el precio final, resta el precio inicial y el descuento en pesos, 85 menos 21.25 igual a 63.75 pesos.
Ahora sí ya puedes contestar las preguntas.
Analiza la tabla y responde los cuestionamientos,
Las preguntas: ¿cuánto se le descontó por cada artículo? Y ¿cuánto pagó por cada uno? Ya las respondimos al completar la tabla.
Para responder las preguntas: ¿cuánto pagó en total?, ¿Cuánto dinero ahorró con su compra? Analiza nuevamente la información.

De acuerdo con la tabla puedes calcular cuánto pagó en total Kinerette, basta con sumar el precio final de todos los artículos: blusón precio con descuento de 120 pesos, más pantalón de mezclilla de 304 pesos, más playera deportiva de 85.50 pesos, más cinco pares de calcetas de 71.25 pesos más el mallón con precio final de 63.75 pesos.
Al sumar todos los valores, la cantidad final que pagará Kinerette es de 644.50 pesos.
Para responder la siguiente pregunta suma las cantidades obtenidas en la columna de descuento, el blusón con un descuento de 40 pesos; más el pantalón de mezclilla, 76 pesos; más la playera deportiva con un descuento de 9.50 pesos; más los 5 pares de calcetas 3.75 pesos; más el mallón 21.25 tenemos; lo que en total suma 150.50 pesos, que representa el dinero que Kinerette ahorró en su compra.
La tercera pregunta:
¿Cuál fue el artículo que le salió más barato a Kinerette?
Para poder dar respuesta a esta pregunta lo que tienes que hacer es comparar las cantidades que aparecen en la sexta columna (precio con descuento), determinar cuál es la menor y así identificarás qué artículo fue el de menor precio. De acuerdo con la tabla, la cantidad menor entre estos artículos corresponde al Mallón delgado que presenta un precio final de 63.75 pesos.
Ya has visto diferentes formas de representar un porcentaje, como calcular el porcentaje que representa una cantidad de otra; y has resuelto problemas en los que tienes que calcular la cantidad final después de aplicar cierto porcentaje.
¿Tienes claros los procedimientos para resolver problemas de este tipo?
El reto de hoy:
Resuelve una situación problema más, relacionada con las prendas de vestir de la tienda Don Fernando.
Melanie quiere comprar un mallón grueso y una camiseta clásica para regalársela a su hermano.
¿Cuál es el precio con descuento de cada prenda?
¿Cuánto tiene que pagar en total?
Observa el procedimiento para responder las preguntas, al término valida tus resultados
El mallón grueso tiene un precio inicial de 115 pesos con descuento de 12 %, determina la relación entre los datos, el 12 % de 115 pesos, 12 % como número decimal se representa como 0.12; por ello, para obtener el porcentaje de descuento multiplica 115 por 0.12 igual a 13.80, que sería el dinero que se descuenta del precio inicial. Ahora para tener el precio con descuento resta el precio inicial y el descuento obtenido 115 menos 13. 80 igual a 101.20 pesos.
Ahora, calcula el precio final de la camisa. Ésta tiene un costo de 120 pesos con un descuento de 25 por ciento. Se representa el 25 % como número decimal: 0.25, y se multiplica por el precio inicial.
Así tienes 120 pesos por 0.25 igual a 30 pesos. Ahora, para obtener el precio final con descuento resta al precio inicial y el descuento obtenido: 120 menos 30 igual a 90 pesos.
Es momento de responder las preguntas.
¿Cuál es el precio con descuento de cada prenda?
Podemos observar que el mallón grueso tiene un precio final de $101.20, la camisa clásica un precio final de $ 90.00.
¿Cuánto tiene que pagar en total?
Para responder, suma el precio de ambas prendas, 101.20 pesos más 90 pesos es igual a 191.20 pesos.
Con esto has dado respuesta al problema de las compras de Melanie.
Comparte tus experiencias con tu profesora o tu profesor en algún momento de tu retroalimentación en tus clases en línea. Así mismo, te invito a poner en práctica las estrategias vistas, revisa tu libro de Matemáticas de primero y resuelve algunos ejercicios similares a los que trabajaste.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas