Signos de agrupación en la jerarquía de operaciones
Signos de agrupación en la jerarquía de operaciones
Aprendizaje esperado: determina y usa la jerarquía de operaciones y los paréntesis en operaciones con números naturales, enteros y decimales (para multiplicación y división, solo números positivos).
Énfasis: aplicar la jerarquía de operaciones, usando signos de agrupación.
¿Qué vamos a aprender?
Aprenderás la importancia de utilizar los signos de agrupación en una cadena de operaciones.
¿Qué hacemos?
No es lo mismo decir: ¿Cómo estás?” que “¡Como estas!” o “¡¿Cómo?!, ¡¿Estás?!” Tanto al hablar como al escribir y sobre todo al leer un texto, es muy importante hacer énfasis en la forma en que hablamos o en la manera de cómo expresamos nuestras ideas por escrito.
Observa el siguiente video del minuto: 02:18 a 03:46, que hace referencia a la forma en que nos expresamos y posteriormente lo relacionarás con la asignatura de matemáticas.
- La importancia de puntuar un texto
https://www.youtube.com/watch?v=oXgQgZjYSF4&feature=youtu.be
Observaste que, en el lenguaje escrito, existen signos que permiten cambiar el sentido de lo que se dice y con ello dar diferentes interpretaciones. En las matemáticas sucede lo mismo, existen signos y símbolos que pueden cambiar el resultado en una cadena de operaciones, así como cambiar el orden que se debe seguir para resolver correctamente un problema o una operación.
En esta sesión continuarás resolviendo operaciones con la Jerarquía de Operaciones, pero observarás que hay símbolos que pueden modificar el resultado final, de acuerdo al uso que les demos. Verás que estos signos y símbolos matemáticos se les denomina: “Signos de Agrupación”.
Un dato interesante sobre un matemático italiano.

Se trata de Niccolo Fontana, conocido como “Tartaglia”, que vivió en el siglo XVI y fue el primero en usar paréntesis para agrupar números y sus operaciones.
Para entender cómo se comporta la naturaleza, los científicos utilizan fórmulas matemáticas para representar y realizar cálculos para resolver problemas. Para poder utilizar estas fórmulas necesitamos conocer las reglas de la jerarquía de operaciones y los signos de agrupación.
Estos signos de agrupación facilitan los procedimientos aritméticos, tanto en fórmulas complejas como en situaciones cotidianas. Observa el siguiente ejemplo:
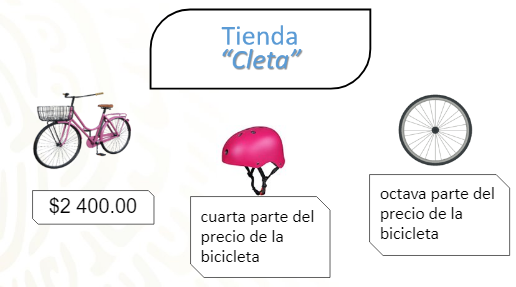
En la tienda “Cleta”, el precio de una bicicleta es de 2400 pesos, el casco de protección cuesta la cuarta parte del precio de la bici y dos llantas de refacción, cada una con un precio de una octava parte, del costo de la bicicleta, ¿cuál es el precio total que debemos pagar por todos los productos?
Analicemos el enunciado, para extraer los datos relevantes y escribirlos, con el objetivo de realizar el planteamiento correcto de las operaciones que se utilizarán para llegar a la solución del problema.
Los datos relevantes son los siguientes:

El costo de la bicicleta es de 2400 pesos, el costo del casco es la cuarta parte de la bicicleta por lo que se expresa como 2400 entre 4, una llanta cuesta la octava parte del costo de la bicicleta y se expresa como 2400 entre 8 y por último la pregunta ¿Cuál es el precio total que debemos pagar por todos los productos?
Podemos realizar el siguiente planteamiento para dar respuesta a este problema:
Iniciamos adicionando los precios de cada uno de los artículos, pero como dos artículos están en función del precio de la bicicleta, usaremos los signos de agrupación tal como se muestra en la imagen.
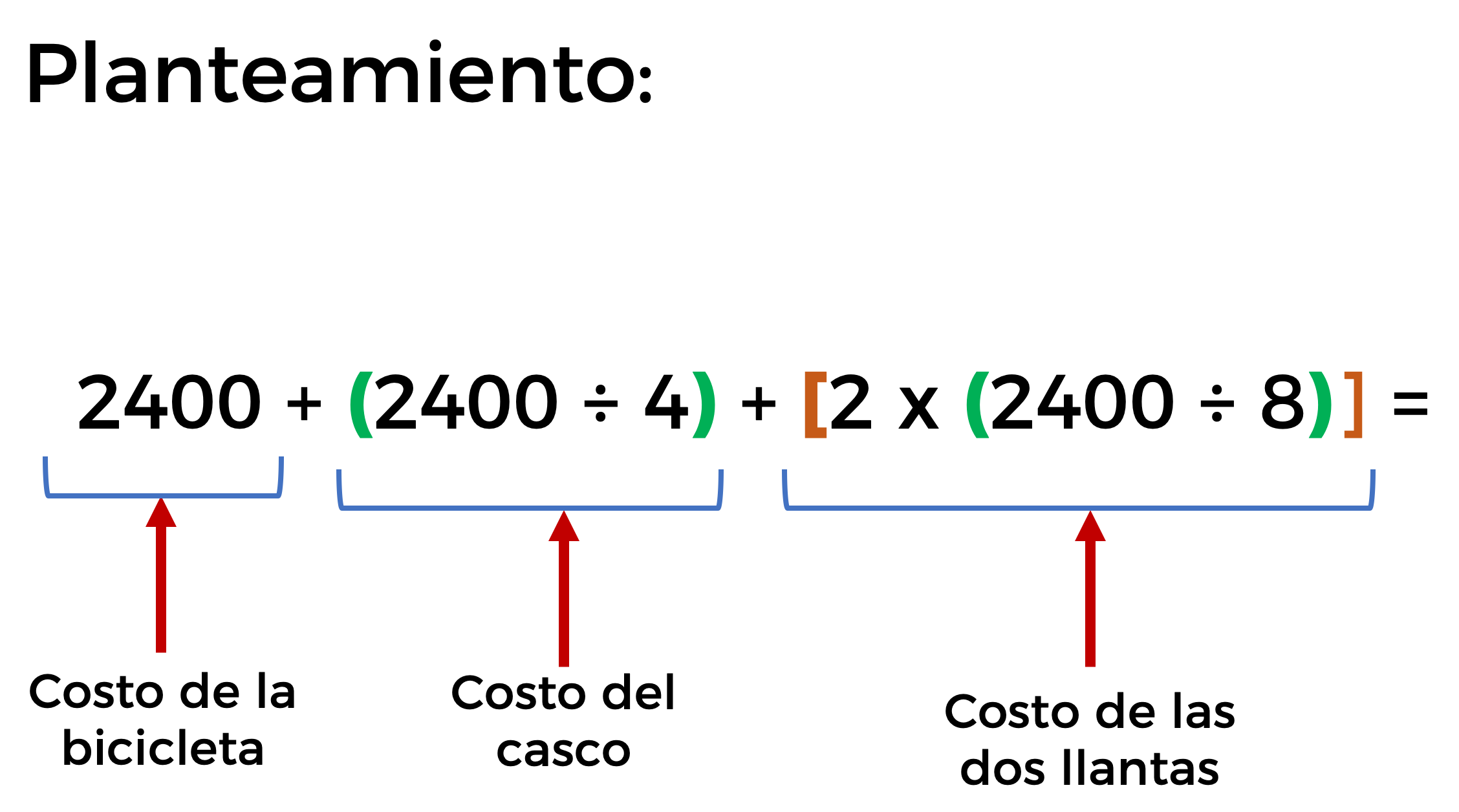
Observen que en el planteamiento aparecen signos que conoces como paréntesis; signos que se utilizan en el lenguaje escrito o en la asignatura de Lengua Materna para acotar una oración que se intercala en otra con la que está relacionada, pero en Matemáticas se utilizan para agrupar operaciones que jerarquizan el orden en que se tienen que resolver.
Primero debemos realizar la división para obtener el costo del casco: en este caso dividimos 2400 entre 4 y el resultado es 600.
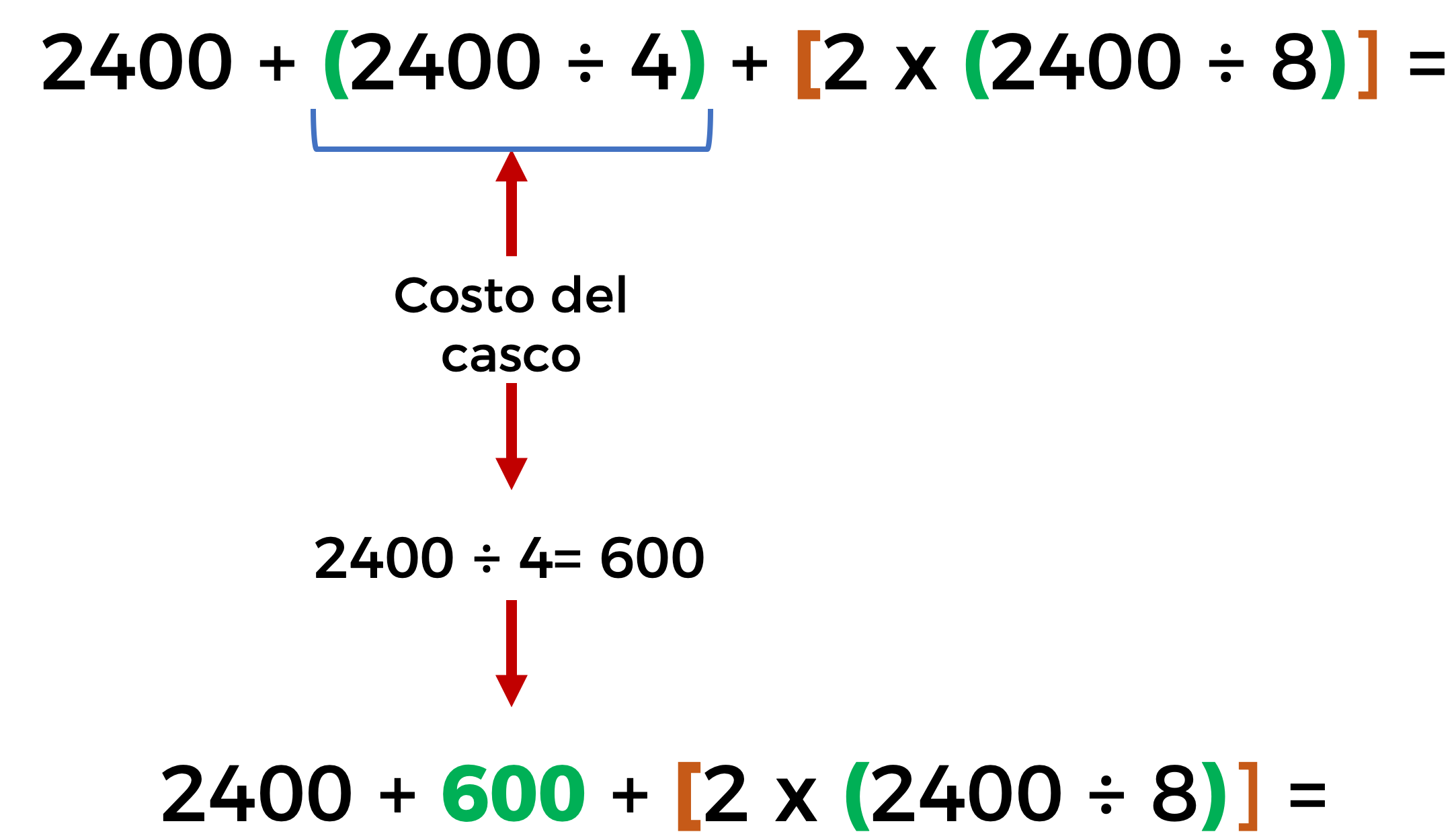
Después obtenemos el costo de las dos llantas, donde cada llanta vale una octava parte del costo de la bicicleta, así que dividimos 2400 entre 8 el resultado es 300. Como observaron en esta parte de la operación resolvimos primero la división para eliminar los paréntesis, y como son dos llantas multiplicamos por 2 y el resultado es 600.
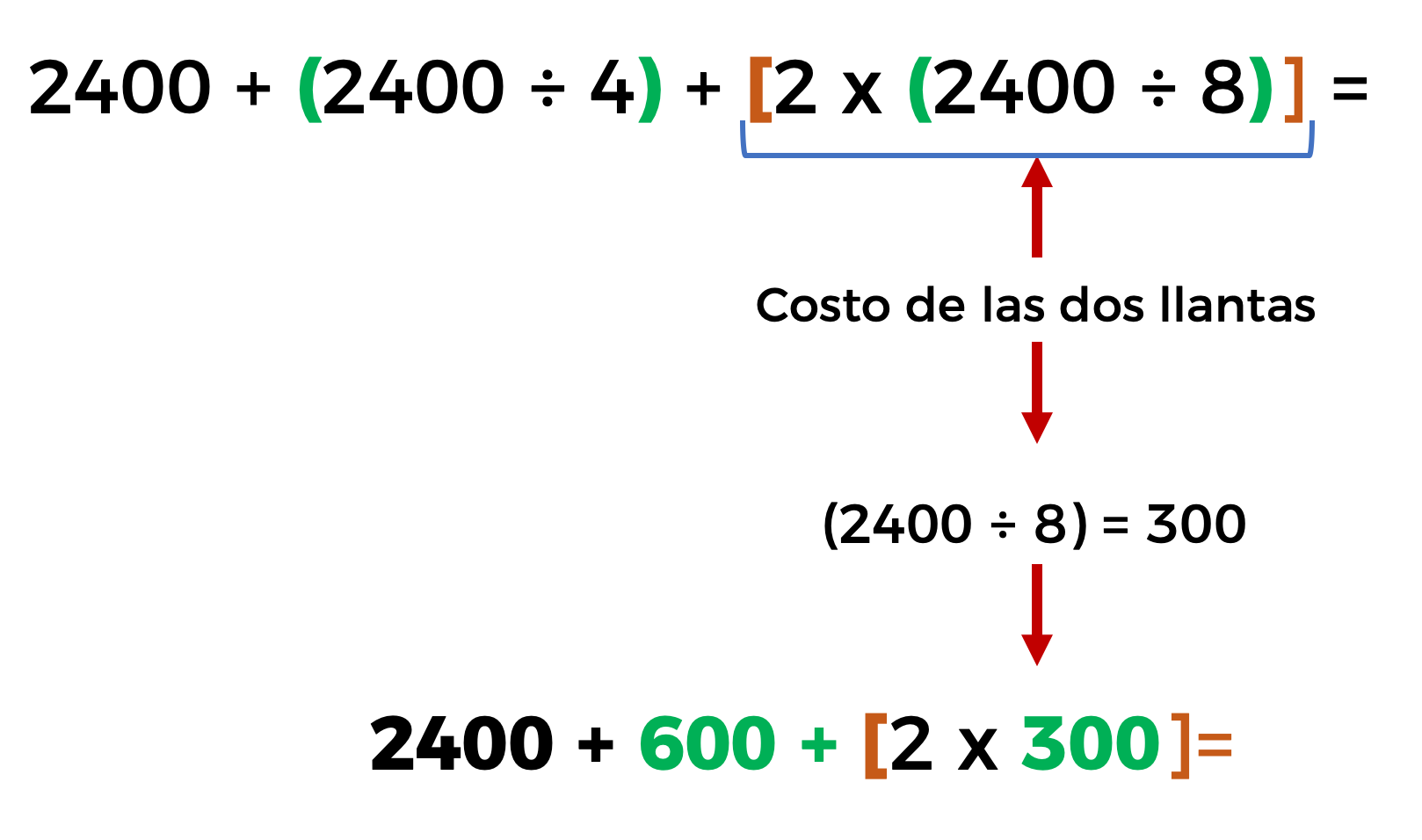
Por lo tanto, el costo total a pagar por todos los productos es $3600 pesos.
Pues es el resultado de sumar 2400 pesos de la bicicleta más 600 pesos del casco más 600 pesos de las dos llantas.
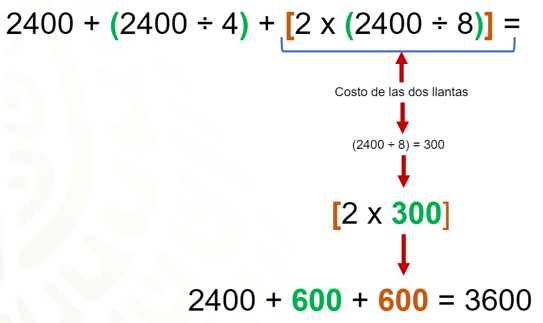
Analiza el proceso que seguimos hasta ahora y responde en tu cuaderno:
¿Qué signos se emplearon?, ¿para qué sirvieron esos signos usados en la cadena de operaciones?
Esos signos de agrupación sirven para dar prioridad a las operaciones que están dentro de ellos. En Matemáticas, estos signos se llaman:
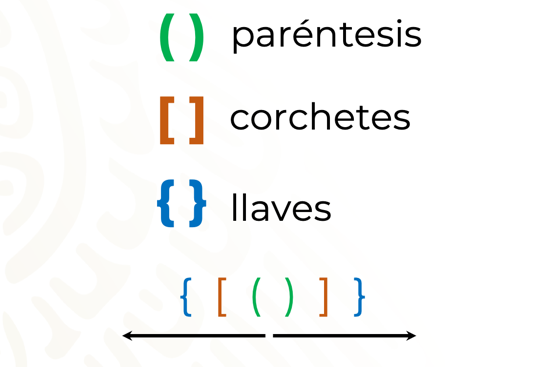
Las llaves y los corchetes tienen la misma función que los paréntesis. Ya que en una misma operación podemos tener la combinación de operaciones, como la suma, resta, multiplicación y división con números enteros, decimales y fraccionarios.
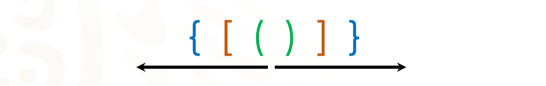
En tu libro de texto, en el tema correspondiente podrás encontrar la siguiente información:

Agrupar las operaciones nos ayuda a resolver de manera correcta situaciones de nuestra vida, por ejemplo, comprar determinado número de artículos de un mismo producto y saber el costo total que debemos pagar, así también para determinar el promedio de calificaciones o puntaje en competencias deportivas.
Planteamos un problema: En una librería están ofreciendo una gran variedad de libros a un excelente precio y además en la compra de más de 5 libros, descuentan 50 pesos al pagar en la caja. ¿Cuál sería el costo total si llegas a comprar dos cómics, tres libros de ciencia-ficción y dos novelas románticas?

Analizando el problema determinemos los datos relevantes, que en este caso es el costo unitario de cada libro:
Cómics $ 150.50
Ciencia Ficción $ 230.20
Novelas románticas $ 180.40
Otro dato relevante es el descuento que se hace si se compran más de 5 libros, el cual es de $ 50.00.
Realicemos el planteamiento de acuerdo a los datos del problema para determinar el costo total a pagar de los libros.

De acuerdo a la pregunta, observamos que se van a comprar: 2 cómics, 3 libros de ciencia ficción y 2 novelas románticas, haciendo un total de 7 libros adquiridos, por lo que se aplica el descuento correspondiente. Con estos datos se genera la siguiente expresión aritmética:
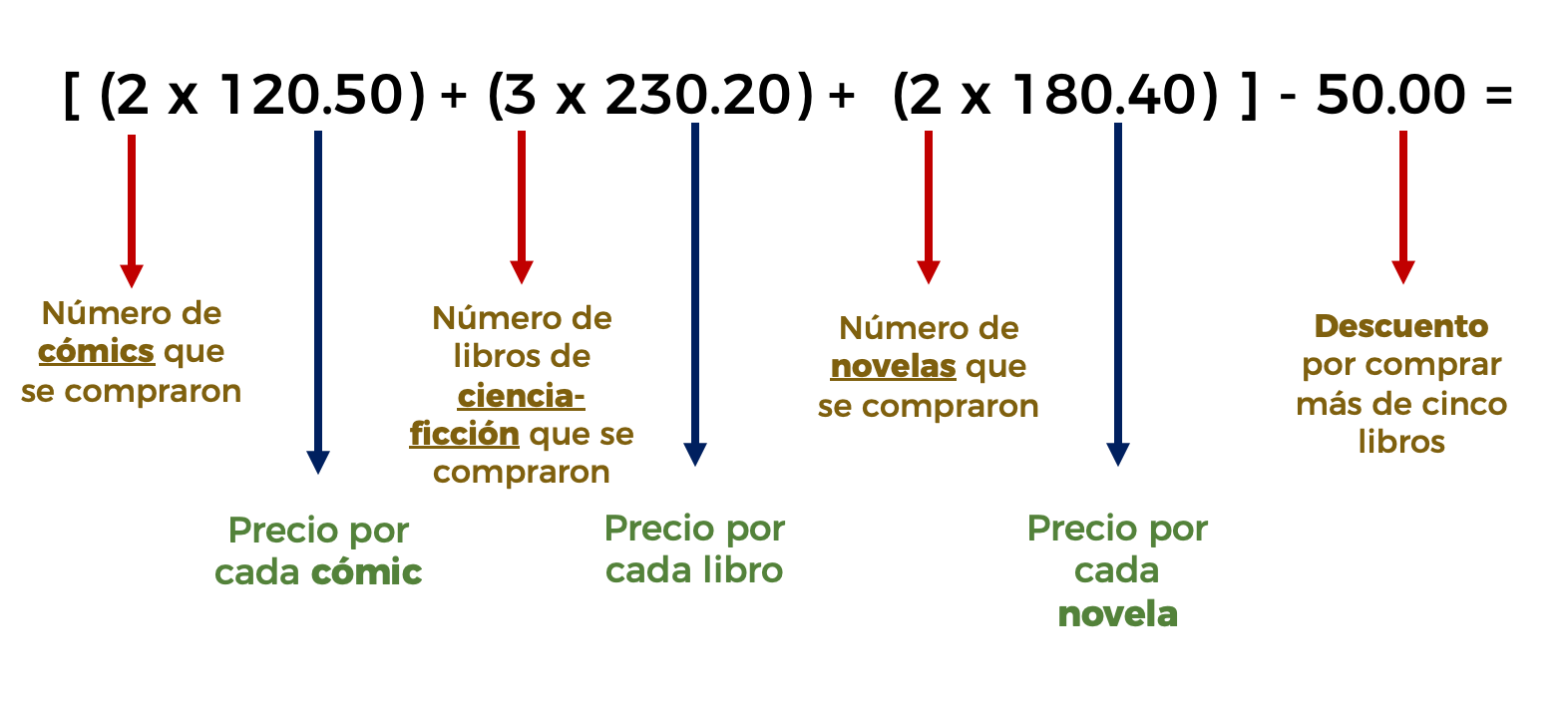
En la primera operación tenemos: el número de cómics por su costo unitario; más el número de libros de ciencia ficción por su costo unitario; más el número de libros de novelas por su costo unitario, cada operación se agrupa entre paréntesis y como al resultado de esta sumatoria le vamos a restar el descuento por comprar más de cinco libros entonces se hace necesario agrupar las sumas con un par de corchetes.
Resolvemos las operaciones que se encuentran dentro de los paréntesis; para este problema son multiplicaciones.
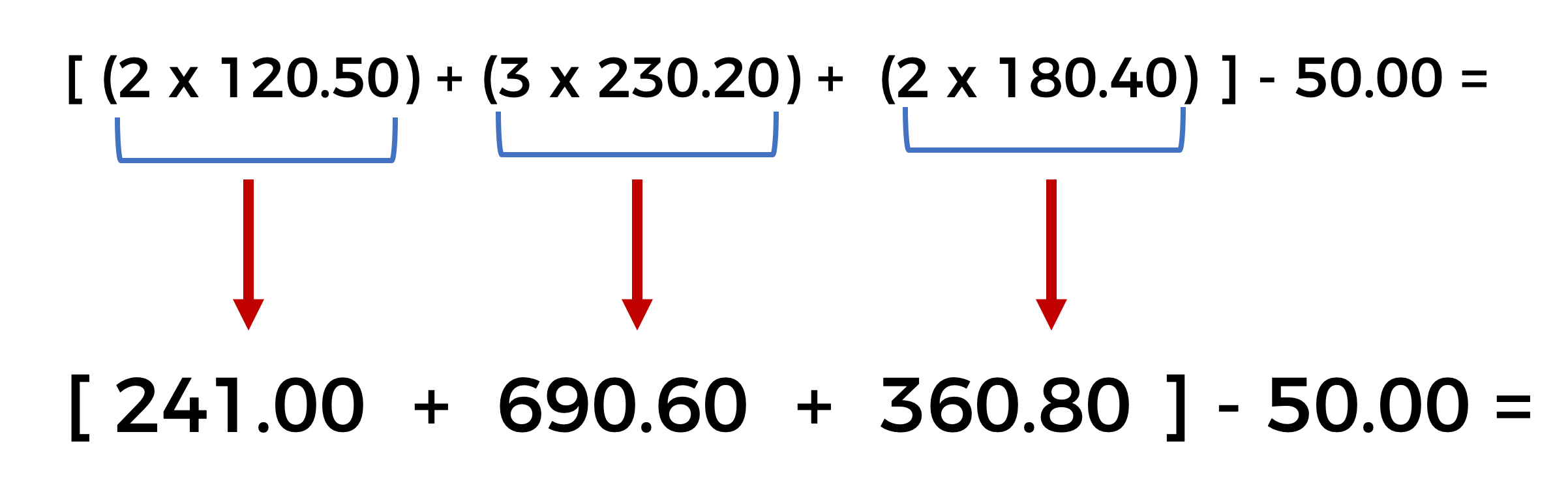
Realizamos el producto de 2 por 120.50, obteniendo doscientos cuarenta y uno, después el producto de 3 por 230.20, obtenemos como resultado seiscientos noventa puntos sesenta. Por último, el producto de 2 por 180.40, resultando en trescientos sesenta puntos ochenta.
Después de realizar las multiplicaciones, se resuelve la adición que está dentro del corchete de la siguiente manera:
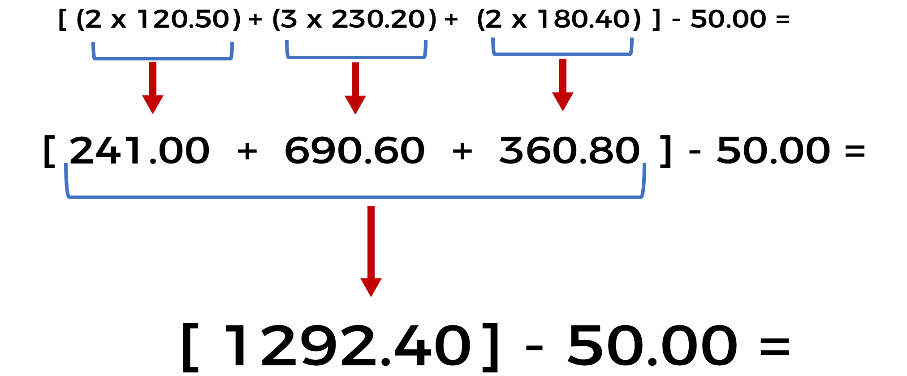
Doscientos cuarenta y uno, más seiscientos noventa puntos sesenta, más trescientos sesenta puntos ochenta, dando como resultado mil doscientos noventa y dos puntos cuarenta.
241 + 690.60 + 360.80 = 1292.40
A la cantidad resultante se le resta, el descuento, por la compra de más de cinco libros, es decir $1292.40 menos $50.
Aplicando correctamente la jerarquía de operaciones y los signos de agrupación, llegamos a la cantidad que debemos pagar en la caja, siendo igual a:
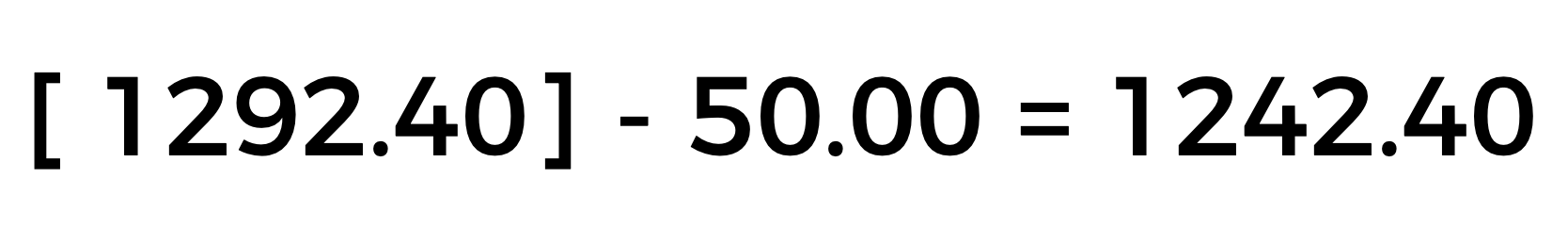
Las matemáticas están presentes en cualquier contexto, tal es el caso de los deportes cuando es necesario comparar los puntajes obtenidos en alguna competencia.
Consideremos como ejemplo a una gran deportista que ha representado a nuestro país en competencias internacionales siendo considerada la mejor clavadista de la historia de México: Paola Espinosa.
En el año 2012, en los Juegos Olímpicos que se realizaron en Londres, Paola Espinosa, en la fase final de una de las pruebas, obtuvo las siguientes valoraciones:
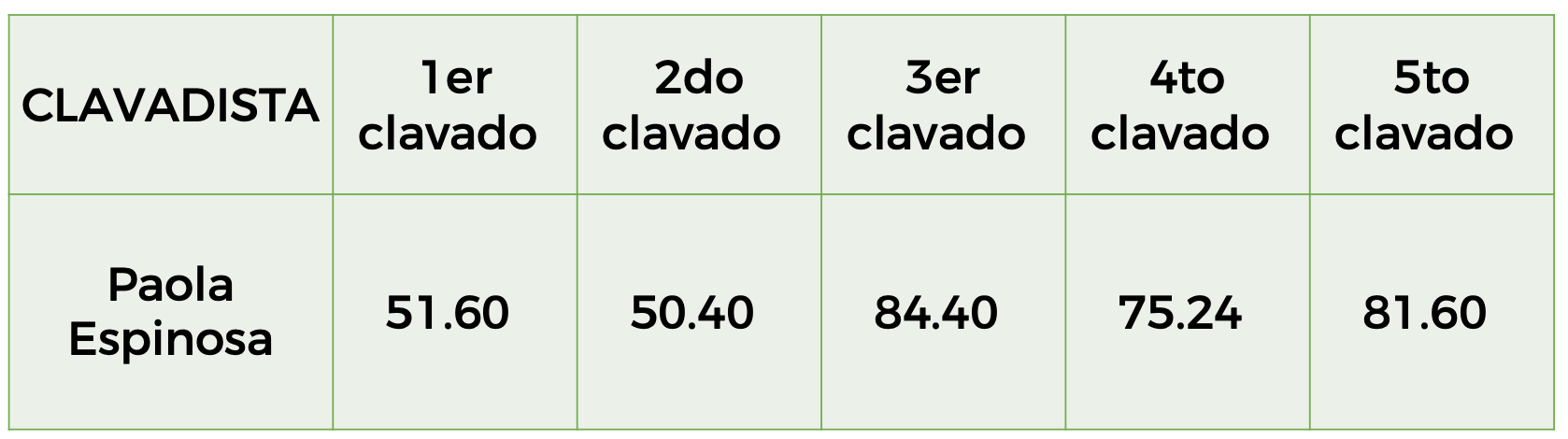
¿Cuál de las siguientes operaciones es la correcta que se debe plantear para obtener el promedio de los puntos obtenidos durante su participación?

La segunda opción es la forma correcta para dar solución al problema.
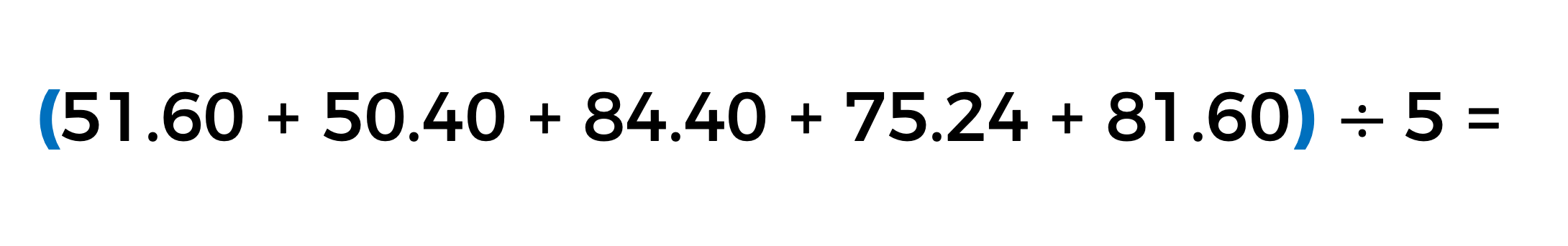
Independientemente de que en las tres operaciones aritméticas existe una “Jerarquía de Operaciones”, en el segundo planteamiento se utiliza un signo de agrupación, llamado paréntesis, el cual nos indica el procedimiento que se debe realizar en primer lugar.
Por lo tanto, debemos sumar los datos que se encuentran dentro del paréntesis, quedando de la siguiente manera:

Esta operación es la correcta, porque para calcular su promedio, se deben sumar los puntajes obtenidos, y después dividir el total entre el número de participaciones que tuvo en esta competencia, que en este caso fueron cinco clavados.
De esta manera, obtenemos que su promedio fue:
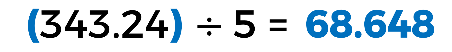
Gracias a esos puntajes obtuvo la medalla de plata durante esos juegos olímpicos al lado de otra gran competidora, Alejandra Orozco.
Recuerda que el éxito de un deportista radica en la práctica diaria, lo mismo pasa en las matemáticas, la práctica te hará experta o experto.
Como pudiste observar el orden en el que se eliminaron los signos de agrupación, va de adentro hacia afuera. Otro aspecto importante es que con los signos de agrupación se puede representar de otra forma la multiplicación.
Esto sucede cuando hay dos signos de agrupación juntos, ya sean dos paréntesis, dos corchetes o la combinación entre ellos y no hay algún signo que indique suma o resta entre ellos, tal como se muestra en la imagen.

Esto nos demuestra que las Matemáticas son abundantes en su simbología, puesto que existen diferentes formas de representar una misma operación.
En los ejercicios anteriores, utilizamos números enteros y números decimales. También empleamos los signos de agrupación como paréntesis, corchetes y llaves, que nos sirvieron para agrupar diversas operaciones. Usar los signos de agrupación nos ayudan a dar orden a las operaciones aritméticas, separándolas para resolverlas, resolviendo de dentro hacia fuera, aplicando la jerarquía correspondiente.
Recuerda que sin los signos de agrupación puedes obtener resultados diferentes o errados, porque no se aplican las reglas de la jerarquía de operaciones, por eso su importancia.
Los signos de agrupación que has aprendido en esta lección sirven para separar operaciones y facilitan el cálculo cuando hay varias operaciones aritméticas, esto te permite saber: cuánto vas a gastar y cuánto te sobra al comprar algo, calcular un promedio, también es útil para llevar la contabilidad personal o de una empresa.
Los signos de agrupación también son utilizados en otras ramas de las Matemáticas como en el caso del Álgebra, la Estadística, la Geometría y la Probabilidad o en otros campos de la Ciencia como la Física, la Química, la Biología, etc.
El reto de hoy:
Te planteamos un reto que tiene que ver con la aplicación de los signos de agrupación que has visto durante esta sesión.
Te proponemos un desafío que está en el libro “El hombre que calculaba”, en donde el personaje principal, al que el autor hace llamar el ingenioso Beremiz, utilizó cuatro cuatros, para formar los números del 0 al 9.
Como sabes, todo reto contiene reglas. Y las reglas para este desafío son las siguientes:

Por ejemplo, para escribir el cero:
Se realiza la sustracción de 44 menos 44.
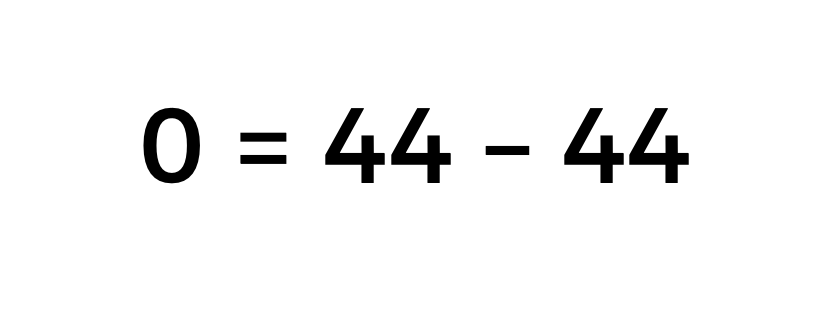
Para este caso se cumplen las reglas del desafío.
En este desafío no es la única forma de representar el cero, puedes aplicar lo que aprendiste y ocupar los signos de agrupación para representar de otra forma el cero.
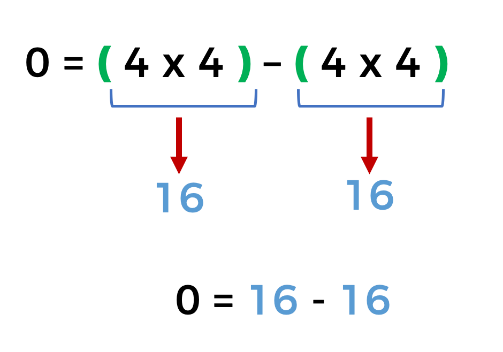
El producto de cada multiplicación es dieciséis, y al realizar la sustracción, obtenemos como resultado cero.
Lo ingenioso de este desafío es que un solo número se pueden representar de otras maneras. Para el mismo cero te proponemos una más.
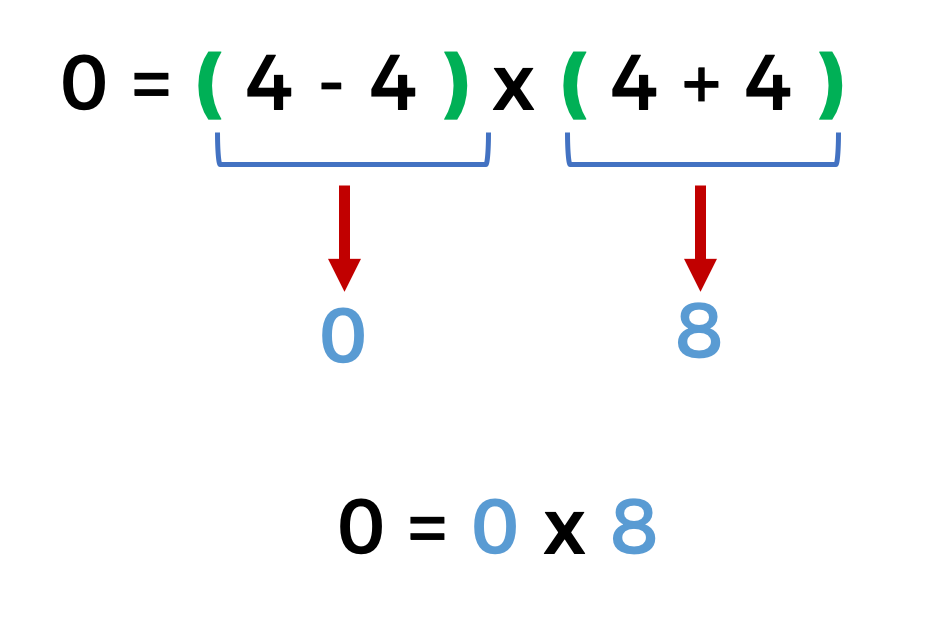
Agrupamos la sustracción de cuatro menos cuatro y la multiplicamos por el resultado de la adición de cuatro más cuatro. Y el resultado es cero.
Ahora, te retamos a obtener el número uno, recuerda que puedes manejar signos de agrupación y los cuatro cuatros, para darle prioridad a la operación a realizar y cumplir con las reglas establecidas en este desafío.
Una forma sencilla de superar este desafío, sin utilizar signos de agrupación es dividir cuarenta y cuatro entre cuarenta y cuatro, dando como resultado uno.
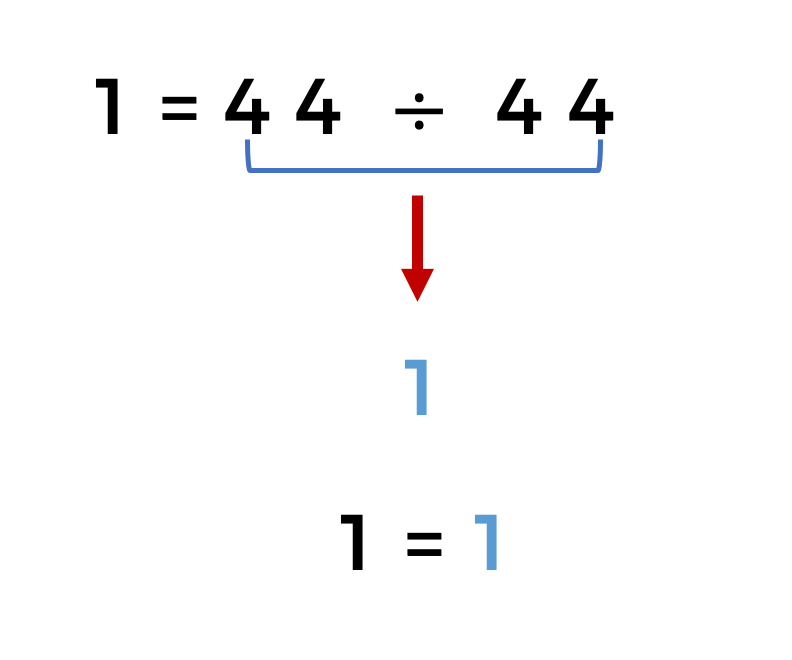
De igual manera podemos encontrar otra forma de obtener el número uno, aplicando los signos de agrupación de la siguiente forma:
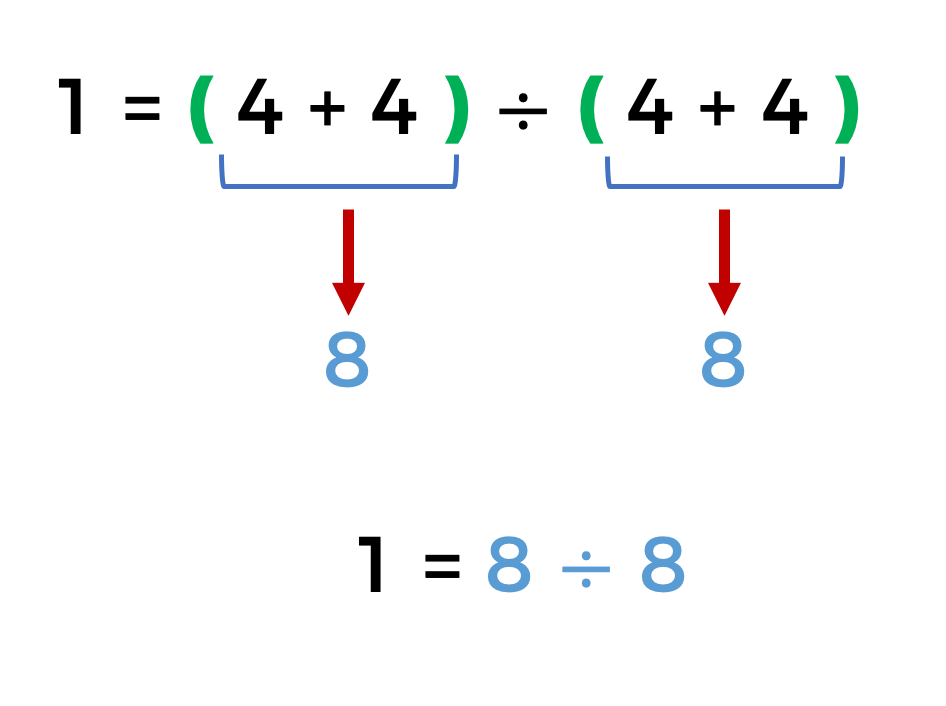
Con los signos de agrupación se da prioridad a las sumas, obteniendo en cada caso ocho, y al dividir ocho entre ocho se obtiene el número uno.
¿Qué resultado se obtendría si no ponemos los signos de agrupación en el mismo planteamiento?
Aplicando la jerarquía de operaciones primero dividimos 4 entre 4, al resultado que es 1, le adicionamos el primer 4, el resultado es 5 y a ese resultado le adicionamos el otro 4, el resultado final es 9.
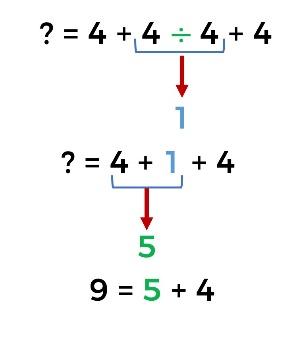
Si te das cuenta al resolver la operación con signos de agrupación, dimos prioridad a las operaciones dentro de ellos y se cumplió el desafío.
Pero, en el segundo caso al no considerar los signos de agrupación, obtuvimos otro resultado. Eso no quiere decir que este mal el ejercicio, solo que no está cumpliendo con el objetivo de obtener como resultado 1.
Te retamos a encontrar los siguientes números: 2, 3 y 4, no olvidando las reglas previamente establecidas al inicio de este desafío, que son:
- Solamente emplear cuatro cuatros y.
- El manejo de las operaciones: adición, sustracción, multiplicación y división, pero además recuerden que en ocasiones es necesario utilizar los signos de agrupación.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/Matemáticas