Resolución de problemas con criterios de congruencia

Resolución de problemas con criterios de congruencia

(Clase de repaso)

Aprendizaje esperado: análisis de la existencia y unicidad en la construcción de triángulos y cuadriláteros.

Énfasis: aplicar los criterios de congruencia de triángulos para probar las propiedades de los paralelogramos.

¿Qué vamos a aprender?

Aplicarás los criterios de congruencia de triángulos, para probar las propiedades de los paralelogramos a través de la resolución de problemas.

¿Qué hacemos?

¿Te has percatado de que al caminar por las calles puedes observar construcciones, áreas naturales y todo tipo de objetos en los que puedes encontrar cuerpos y figuras geométricas? No sólo en el exterior, también en el interior de tu hogar las puedes encontrar; por ejemplo, en las mesas, ventanas, puertas, los retratos, teléfonos celulares, y hasta en los azulejos de los pisos. ¿Las has apreciado? ¿Qué tipo de figuras has encontrado?

Puedes observar por ejemplo: algunos espejos circulares; algunos platos son de forma ovalada, en los balones de futbol hay pentágonos y hasta hexágonos. También hay figuras que están compuestas por dos pares de lados paralelos, ¿sabes a cuáles son? Se llaman paralelogramos. Un paralelogramo es una figura plana en la que sus lados opuestos son paralelos; es decir, que tienen dos pares de lados paralelos. Algunos ejemplos son: los cuadrados, los rectángulos, los rombos y los romboides. Para que los observes a detalle, te mostramos la siguiente imagen.

En la imagen se observan cuatro paralelogramos. En primer lugar el cuadrado; debajo de él, un rectángulo; el rombo al lado derecho; y arriba a la derecha, un romboide.

Para realizar un análisis de esta clasificación de figuras, las propiedades de un paralelogramo son las siguientes:

Primera propiedad, la suma de los cuatro ángulos internos es igual a 360°; para que lo observes, pon atención al siguiente video:

Propiedades de un paralelogramo
Del minuto: 00:00 al 01:12
https://youtu.be/OeUzGP9d9PI
Segunda propiedad: Un par de ángulos contiguos son suplementarios, compruébalo observando el siguiente video:
Propiedades de un paralelogramo
Del minuto: 01:13 al 02:02
https://youtu.be/OeUzGP9d9PI
La tercera propiedad enuncia que los ángulos internos opuestos miden lo mismo; analízalo con el siguiente video:
Propiedades de un paralelogramo

Del minuto: 02:03 al 02:48

https://youtu.be/OeUzGP9d9PI

La cuarta propiedad indica que las dos diagonales dividen al paralelogramo en dos triángulos congruentes, lo cual puedes observar en la siguiente imagen.

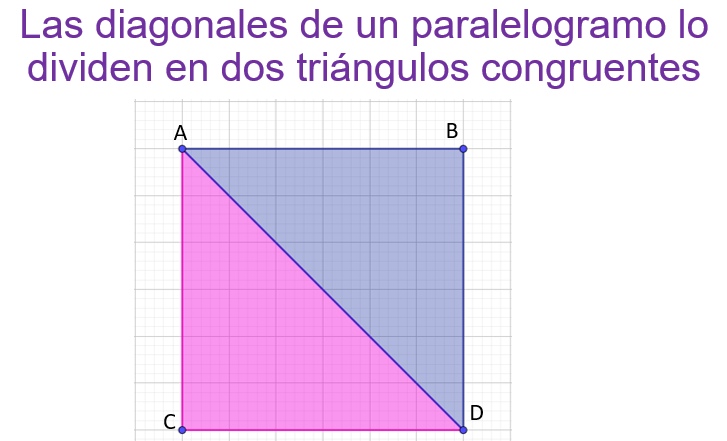
En la imagen puedes identificar un paralelogramo, el cual está dividido en triángulos de diferente color, formados por las dos diagonales del paralelogramo, comparten uno de sus lados con cada diagonal del paralelogramo.

Dos o más triángulos son congruentes cuando son iguales, tanto en la medida de sus ángulos como de sus lados, es decir: que sin importar la posición en la que se encuentran los triángulos, la longitud de sus lados y la medida de sus ángulos son iguales. Para determinar la congruencia entre dos triángulos cualesquiera, sólo se necesitan tres condiciones mínimas conocidas como criterios de congruencia.

Criterio Lado, Ángulo, Lado (LAL). Si dos lados de un triángulo y el ángulo formado por ellos son congruentes con los que corresponden a otro, se dice que los dos triángulos son congruentes.

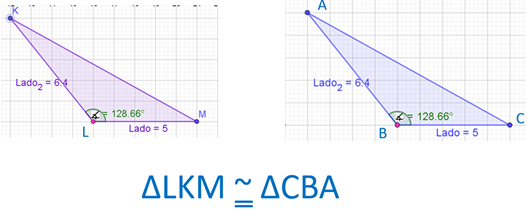
Maestra Carmen VO: Criterio Ángulo, Lado, Ángulo (ALA). Cuando en dos triángulos se tienen dos ángulos y un lado comprendido entre ellos, congruentes; estos triángulos son congruentes.

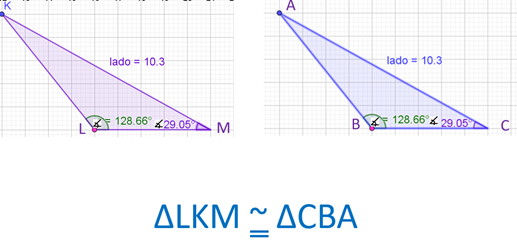
Maestra Carmen VO: Criterio Lado, Lado, Lado (LLL). Cuando se tienen dos triángulos y sus tres lados correspondientes son congruentes, entonces los triángulos son iguales, o congruentes.

Te invitamos a resolver una situación-problema, en este caso, con la aplicación de los criterios de congruencia de los triángulos.

Una lancha atraviesa un río, cuyos márgenes son paralelos. Esa lancha recorre un total de 4 km en línea recta y exactamente a mitad de camino deja caer una boya con un ancla que deberá recoger otra lancha (una boya es un objeto flotante que se emplea a modo de señal). La lancha sale desde la misma orilla y de un punto a 5 km del punto de partida de la primera, y navegando siempre en línea recta recoge la boya al cabo de 4 km. ¿A qué distancia de la primera lancha llega la segunda lancha a la otra orilla? Para poder dar respuesta a esta situación, representamos a partir de trazos el recorrido de la primera lancha.

Para resolver el problema, comenzamos analizando los datos que se proporcionan y modelamos la situación.

El río corre entre dos márgenes paralelos, que representaremos con dos rectas paralelas que llamaremos “r” y “s”. Denotemos por A y B el punto de partida y de llegada de la primera lancha, respectivamente. La lancha deja caer la boya en un punto, que llamamos “O”, exactamente a mitad de camino.

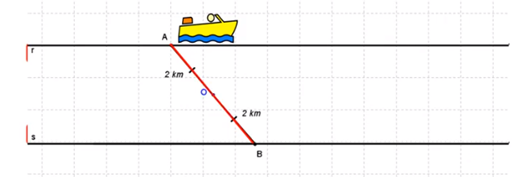
En la modelación, esto quiere decir que “O” es el punto medio del segmento AB. Sabemos que la lancha recorre una distancia total de 4 km, por lo tanto, el segmento AB = 4 km y el segmento AO = al segmento OB = 2 km.

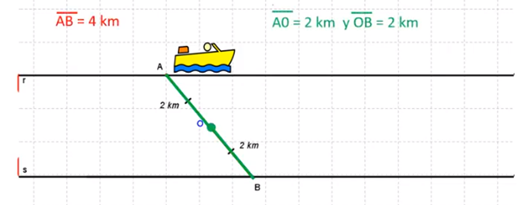
Ahora representamos el recorrido de la segunda lancha, de forma que podamos completar los trazos.

La segunda lancha sale de un punto C de la orilla “r”. Este punto está a 5 km del punto de partida de la primera lancha, lo que quiere decir que el segmento AC = 5 km. La segunda lancha se mueve siempre en línea recta, pasando por “O”. Llega al margen “s” del río en un punto que denotamos por “D”. Como se mueve siempre en línea recta, el punto “O” pertenece al segmento CD. Por último, la lancha recoge la boya, que se encuentra en el punto O, al cabo de 4 km, lo que nos indica que el segmento CO = 4 km. Podemos finalmente realizar el trazo completo de la situación.

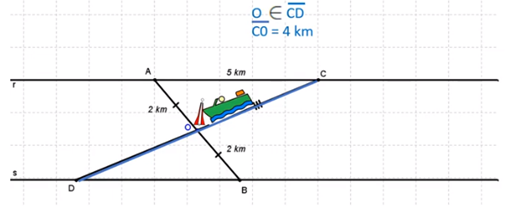
Ya hemos creado un modelo que representa el problema, para resolverlo debemos trabajar con los criterios de congruencia, y al final interpretar los resultados que obtengamos en función de lo que cada uno de los objetos geométricos, que tenemos, representa en la situación real.

El problema pide averiguar la distancia entre los puntos de llegada de ambas lanchas, que en nuestro modelo está representada por la longitud del segmento BD.

Observemos que las rectas “r” y “s” son paralelas, y por lo tanto el ángulo CAO = al ángulo OBD por ser alternos internos entre “r” y “s”, que son paralelas, cortadas por el segmento AB.

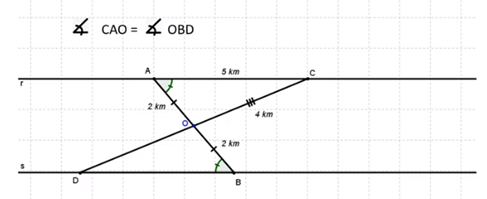
Por otro lado, el ángulo AOC = ángulo BOD por ser opuestos por el vértice y el segmento AO = al segmento OB, por lo tanto son iguales a 2 km. Observa que se forman dos triángulos en los trazos, el triángulo AOC y el triángulo BOD tienen un lado que mide lo mismo, el cual es el segmento AO y el segmento OB que miden 2 km, y los ángulos adyacentes respectivamente congruentes, porque se forman entre rectas paralelas.

Por el criterio ALA resultan congruentes los dos triángulos, y esto nos ayudará a determinar la distancia que el problema nos pide encontrar. Los lados homólogos son el segmento AO y el segmento OB, el segmento OC y el segmento OD y el segmento AC y el segmento BD. Esto implica que el segmento OD = al segmento OC y el segmento AC = al segmento BD.

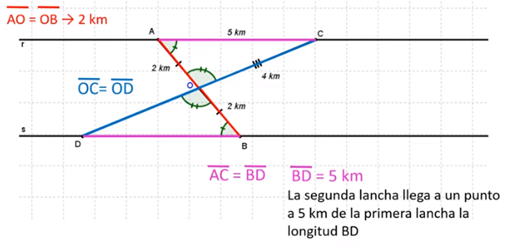
Concluimos que el segmento BD = 5 km. Por lo tanto, la segunda lancha llega a un punto a 5 km de la primera lancha (longitud de BD).

Aplicando un criterio de congruencia resolvimos la situación anterior, demostrando que los dos triángulos que se forman entre los trazos son congruentes; y al ser congruentes, sus ángulos y lados tienen la misma medida.

Es importante que no pierdas de vista que los criterios de congruencia te ayudarán a resolver ciertas situaciones de forma más eficiente a partir de una demostración geométrica.

Ya resolviste una situación que implica utilizar los criterios de congruencia de los triángulos; pero, estos mismos criterios podrían aplicarse a situaciones en donde intervengan el trazo de paralelogramos. Para ejemplificarlo utilizarás una situación que puedes encontrar en su libro de texto de Matemáticas, de primer grado.

Un gato hidráulico sirve para levantar automóviles, y está diseñado como se muestra en la imagen:

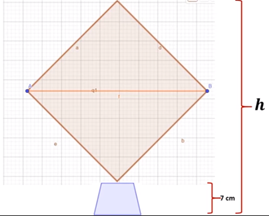
Puedes observar en la imagen un gato hidráulico que al manipularse forma un cuadrado, cuyos lados miden 33 centímetros; a su vez está dividido por un tornillo en su diagonal horizontal, que lo representamos como el segmento AB con una longitud de 46.7 centímetros, sostenido por uno de sus vértices; apoyado en una base que mide 7 centímetros de altura. Si el eje entre los puntos A y B mide 46.7 centímetros cuando el gato tiene la forma de cuadrado, aproximadamente, ¿a qué altura levantará un automóvil?

Conforme a la situación planteada, lo que necesitamos conocer es la altura a la que se levanta un automóvil sabiendo que el gato hidráulico está apoyado en una base que mide 7 cm, por lo tanto, requerimos determinar esta longitud.

Comenzaremos analizando los datos que nos proporcionan y realizamos un trazo que represente la situación. El gato hidráulico está extendido de tal manera que su forma se asemeja a la de un cuadrado, por lo que marcaremos sus dos vértices faltantes con el punto D y el punto E. Observa que se forman dos triángulos, uno de ellos es el triángulo ABE y el otro es el triángulo ADB.

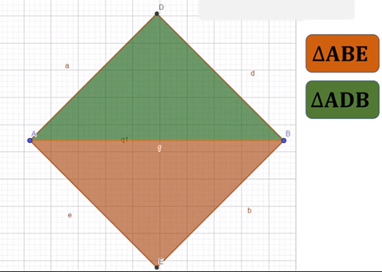
El segmento AB mide 46.7 cm, ya que este dato lo proporciona el problema; este segmento es un lado que forma parte de los dos triángulos. Observa qué tipo de triángulos se forman, son triángulos rectángulos, y una de sus características es que tienen un ángulo recto, es decir, miden 90°. Observa que el segmento AD y BE son paralelos; así que el ángulo ABE y el ángulo DAB son alternos entre paralelas y por lo tanto miden lo mismo, en este caso 45°. Así que el triángulo ABE es congruente con el triángulo ADB por el criterio ÁNGULO-LADO-ÁNGULO (ALA).

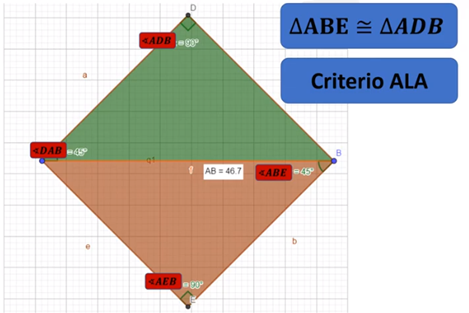
Al mismo tiempo, una de las propiedades de los paralelogramos, enuncia que su diagonal lo divide en dos triángulos congruentes. Tracemos la otra diagonal, perpendicular a la ya trazada, y se formarían de nuevo dos triángulos congruentes.

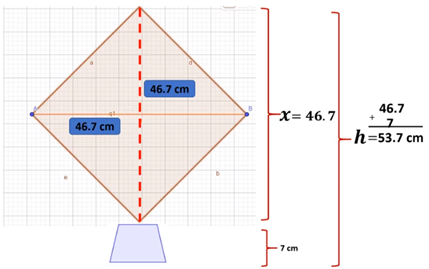
MAESTRO DAVID V.O (Con’t) Los triángulos que se forman con las diagonales tienen las mismas medidas de lados y ángulos, es decir, son congruentes; por lo tanto, podemos concluir que el segmento DE mide lo mismo que el segmento AB, porque estamos hablando de triángulos congruentes y sus lados deben tener las mismas medidas; así que mide 46.7 cm.

Conforme a la demostración anterior, ya puedes dar respuesta a la pregunta: ¿A qué altura levanta el gato hidráulico un automóvil? Ya sabes que la altura del gato hidráulico es 46.7 cm, eso lo tendrás que sumar con la medida de la base, no olvides que el gato tiene una pequeña base que mide 7 cm. Suma 46.7 más 7 y el resultado es 53.7 cm, que es la elevación del automóvil.

Los criterios de congruencia te ayudan a resolver situaciones de forma más eficiente. Mediante la observación de las figuras geométricas, puedes encontrar soluciones a ciertas medidas; no olvides que los criterios de congruencia son los siguientes:

Lado, Ángulo, Lado (LAL).
Ángulo, Lado, Ángulo (ALA)
Lado, Lado, Lado (LLL)

Los paralelogramos también nos permiten identificar elementos que pueden ser congruentes, sobre todo cuando los dividimos en triángulos y de esta forma aplicamos los criterios de congruencia de los triángulos. Reconociendo un paralelogramo, este es un cuadrilátero con dos pares de lados paralelos y éstos son: cuadrados, rectángulos, rombos y romboides. Al mismo tiempo recuerda que aunque existan distintos paralelogramos, conservan las mismas propiedades entre las que se encuentran: los cuatro ángulos interiores suman 360°, sus pares de ángulos contiguos son suplementarios, los ángulos opuestos son iguales y sus diagonales dividen al paralelogramo en dos triángulos congruentes.

El reto de hoy:

¿Has observado alguna vez vitrales? Quizá conoces uno que está ubicado en Toluca, Estado de México; en el jardín botánico, y que es conocido como: el Cosmovitral.

Como reto, les proponemos lo siguiente:

Identifica en el vitral los triángulos congruentes; te sugerimos, como estrategia ante situaciones semejantes, colorear los pares de triángulos con un mismo color y analizar en cada caso qué criterio de congruencia utilizaste.