Relaciones lineales no proporcionales
Relaciones lineales no proporcionales
Aprendizaje esperado: lee y representa, gráfica y algebraicamente, relaciones lineales y cuadráticas.
Énfasis: analizar las representaciones de una relación lineal no proporcional.
¿Qué vamos a aprender?
Tratarás ejercicios que corresponden a una relación no proporcional y, para ello, estudiarás y resolverás diversas situaciones.
Ten a la mano cuaderno y lápiz para tomar apuntes de aquello que consideres importante.
No es necesario que escribas todo, puedes hacer uso de las palabras clave. Como sugerencia, subraya en tus apuntes, con colores distintos, el concepto de una relación no proporcional y los pasos a seguir para representarla.
¿Qué hacemos?
Comienza por resolver ejercicios, que consisten en plantear una situación que corresponda a una relación no proporcional y explicar cómo puede representarse por medio de una gráfica, una tabla y una expresión algebraica.
Pero antes, repasarás lo aprendido en las clases anteriores, con la siguiente situación.
Una tienda publicó un aviso para contratar vendedores de sus nuevos productos:

¿Qué plan de ventas te conviene elegir?
De acuerdo con lo que se nota en el anuncio, te conviene tener un sueldo y aparte una comisión por artículo que se venda.
Comprueba si esto es lo ideal, primero te apoyarás en un registro tabular.
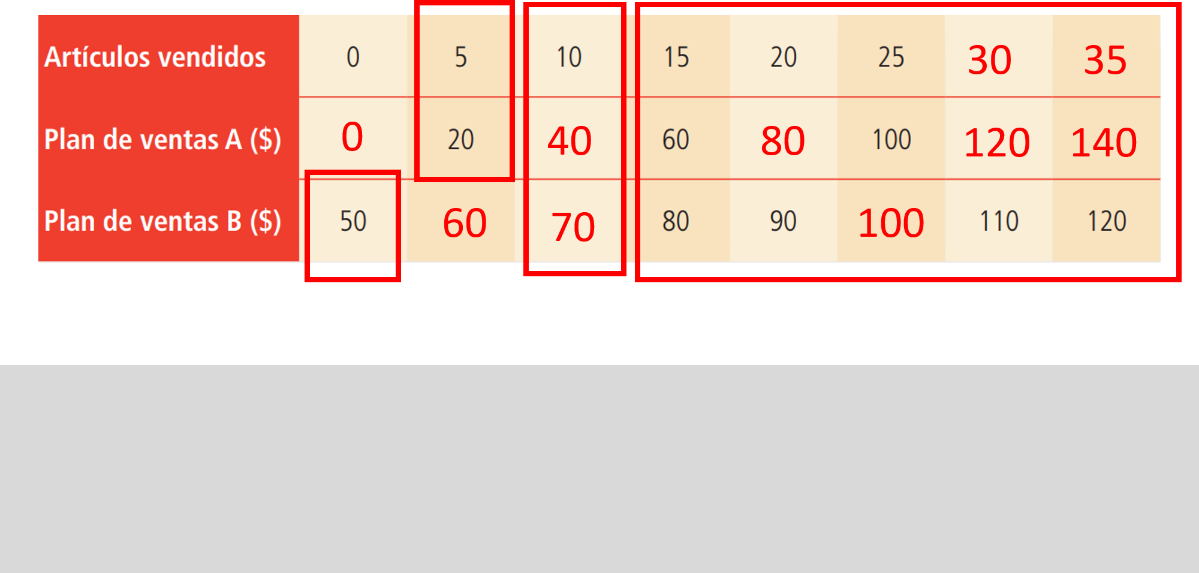
Completa la tabla. Como puedes observar, faltan algunos datos. Analiza:
Primero, cuando no se vende ningún artículo en el plan de ventas A, ganaría 0 pesos; con el plan B tendría los 50 pesos de sueldo base a la semana.
Si se venden 5 artículos, ¿cuánto se obtendría en el plan A y cuánto en el plan B?
Recuerda que en el plan de ventas A se pagan 4 pesos por artículo, por lo tanto, si se venden 5, el sueldo sería de 20 pesos.
En el plan B pagan 2 pesos por artículo vendido, así que al vender 5 se obtendrían 10 pesos y se agregan los 50 pesos del sueldo base para obtener 60 pesos.
De la misma forma se calcula cuando 10 artículos se han vendido, 10 por 4 = 40 para el plan A, y 10 por 2 más 50 = 70 para el plan B.
Así sucesivamente puedes obtener cuando se venden 15 artículos, 20, 25, 30 y 35 para este caso.
Te diste cuenta de que en algunos casos conviene más el plan A, por los cuatro pesos de comisión, y en otros, el plan B, por el sueldo base con el que se cuenta más los dos pesos de comisión.
Analiza la tabla de nuevo; la pregunta sería: ¿cuándo conviene más el plan B que el A? Es cuando vendes menos de 25 artículos.
¿Y para qué convenga más el plan A? En este caso sería cuando vendes más de 25 artículos, ya que obtendrías mayor pago por lo que vendas. Y lo puedes ver en la tabla de forma más clara.
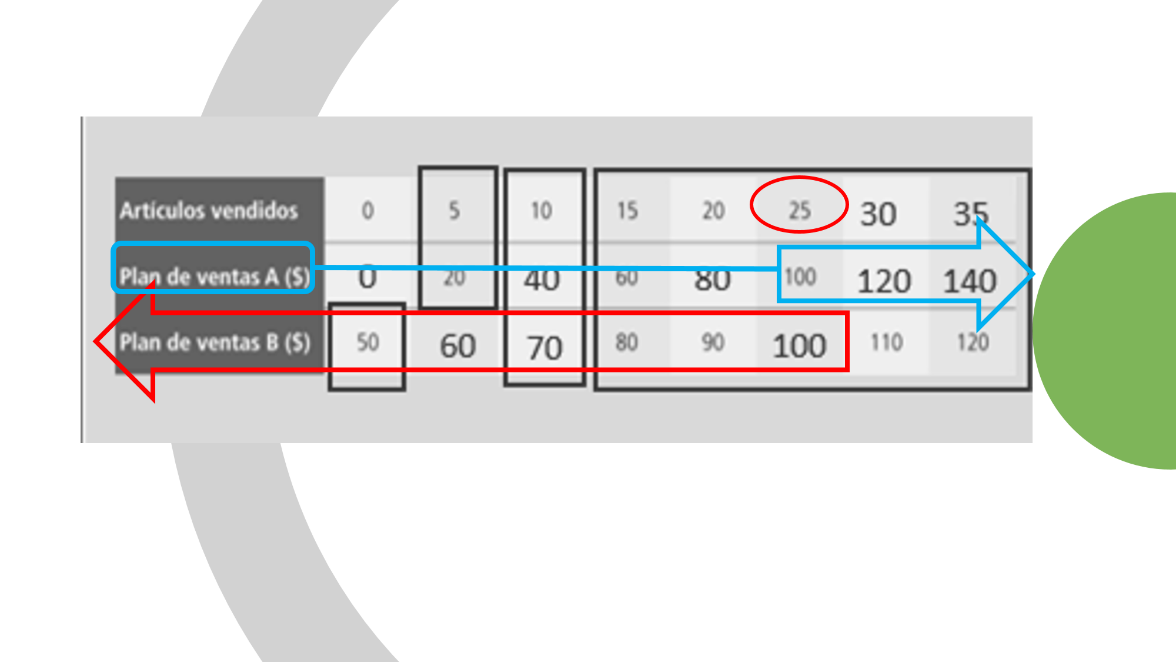
Si observas ambos planes, la relación entre el número de artículos vendidos y el pago es de variación lineal, ya que entre más se vende, más se gana.
Ahora observa cómo se puede obtener la razón de cambio y la expresión algebraica, en donde “y” representa el pago y “x”, la cantidad de artículos vendidos.
Recuerda que la razón de cambio es el cociente de dos cantidades, esto es, una comparación entre dos cantidades. Observa:
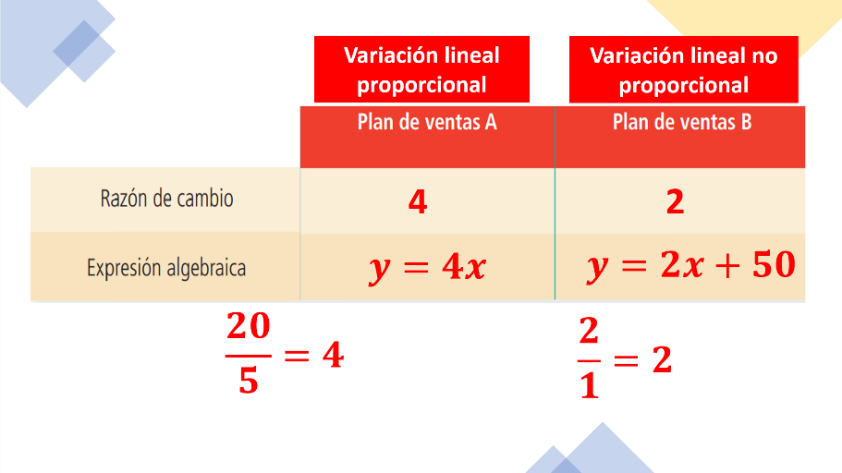
Para el plan A la razón de cambio es 4, ya que si obtienes 20 pesos de sueldo y lo divides entre 5 artículos que se venden, obtienes un cociente de 4, y si comparas los demás datos sucesivamente, obtendrás el mismo cociente.
Por lo tanto, la expresión algebraica es: y = 4x, que indica que para calcular el pago “y” se multiplica por 4 la cantidad de artículos vendidos “x”.
Así, la expresión algebraica representa una variación lineal proporcional.
En el plan B la razón de cambio es 2, en este caso, recuerda que pagan esta cantidad por cada artículo vendido. “y = 2” y “x = 1”, por lo tanto, 2/1= 2.
Entonces, la expresión algebraica y = 2x + 50 indica que para calcular el pago “y” se multiplica 2 (razón de cambio) por la cantidad de artículos vendidos “x”, y se suma 50 (sueldo base).
Este tema de la función lineal que acabas de aplicar, se descubrió desde el siglo XIV, con los filósofos medievales, cuando surgió la inquietud de cómo poder medir y representar gráficamente las variaciones de ciertas magnitudes.
Como, por ejemplo, la velocidad de un cuerpo o el cambio de temperatura que experimenta un objeto en diferentes puntos.
Pero en París, fue Nicolás de Oresme, quien nació en 1323 y murió en el año 1382 de nuestra era, el primero en utilizar diagramas para representar en el plano magnitudes variables.
Algunos siglos después, un matemático suizo llamado Leonhard Euler, fue el que definió como “funciones” a este tipo de relación entre dos cantidades, y desde el siglo XVIII se desarrolló el tema, e hizo una definición que utilizas hasta hoy.

Nació en Basilea, Suiza, y fue discípulo de otro gran científico, Johann Bernoulli, pero muy pronto superó a su maestro.
Trabajó en las Academias de Ciencias de Berlín y de San Petersburgo, donde escribió la mayor parte de sus obras; es uno de los científicos más detallistas de todos los tiempos.
A pesar de que los últimos 17 años de su vida sufrió una ceguera total, sus obras completas ocupan más de 100 volúmenes.
Euler tuvo 13 hijos, a quienes entretenía recitando La Eneida de memoria (que consiste en un poema épico que consta de 12 libros que cuentan la historia de Eneas, un héroe troyano, una obra escrita por el poeta Virgilio).
Además de literatura y lenguas clásicas, tenía amplios conocimientos de fisiología, medicina, botánica y física.
El estudio de las funciones tuvo gran desarrollo con Euler. Él sugirió que algunas relaciones, como y = 2x + 1, debían ser llamadas funciones.
Euler definía las funciones, en 1755, de la siguiente manera:
“Si algunas cantidades dependen de otras cantidades de tal manera que, si las últimas cambian, las primeras también cambian, entonces las primeras cantidades se llaman funciones de las últimas.”
Es importante conocer que muchos de los conocimientos matemáticos son producto de investigaciones que se llevaron cientos de años, y que no fue la intervención de una sola persona, sino que han colaborado varias para que hoy en día se puedan aplicar estos términos.
Observarás el siguiente video para reafirmar el tema. Recuerda revisar tus notas y escribir palabras clave para que así puedas dar seguimiento al recurso.
Analizarás la diferencia entre variación lineal proporcional y variación lineal no proporcional.
- Expresiones algebraicas de relaciones funcionales
youtube.com/watch?v=y3UWGXHYb-g
Te diste cuenta de las dos formas de expresiones algebraicas:
y = ax + b, para la variación lineal no proporcional, y
y = ax para variación lineal proporcional
Trabaja ahora con una situación cotidiana. Piensa qué sucede cuando en tu casa hierven agua para preparar algún alimento o bebida.
La temperatura del líquido aumentará conforme pase el tiempo. La temperatura y el tiempo son dos cantidades que puedes medir. ¿Cómo crees que variará la primera al cambiar la otra?
:
Observa el siguiente video del minuto 8:23 a 10:11 donde podrás saber el registro que se obtuvo al calentar el agua. Observa de qué tipo de variación lineal se trata. - Pendiente y razón de cambio
youtube.com/watch?v=B_JxNROc-Hc&feature=youtu.be
Acabas de observar un ejemplo de variación lineal no proporcional. La ecuación de la forma y = mx + b es una expresión de variación lineal no proporcional, y puede representarse en tablas o gráficas.
Tienes que recordar que, en un fenómeno lineal, la gráfica correspondiente en una línea recta y su pendiente es igual a la razón de cambio entre las cantidades graficadas.
Observa otra situación de variación lineal no proporcional.
Recuerda que tienes que plantear una situación que corresponda a una relación de no proporcionalidad y explicar cómo puede representarse gráfica, tabular y algebraicamente.
Observa atentamente y recuerda tomar notas relevantes.

Para lograr ver mejor las opciones, lo que puedes hacer es una tabla, su gráfica y obtener también la expresión algebraica.
Observa la tabulación del problema. Primero toma en cuenta que hay que hacer un pago de salida de la bicicleta de 30 pesos para la tarifa 1, es decir, 30 más 15 pesos de la renta de cada hora, obteniendo lo siguiente:
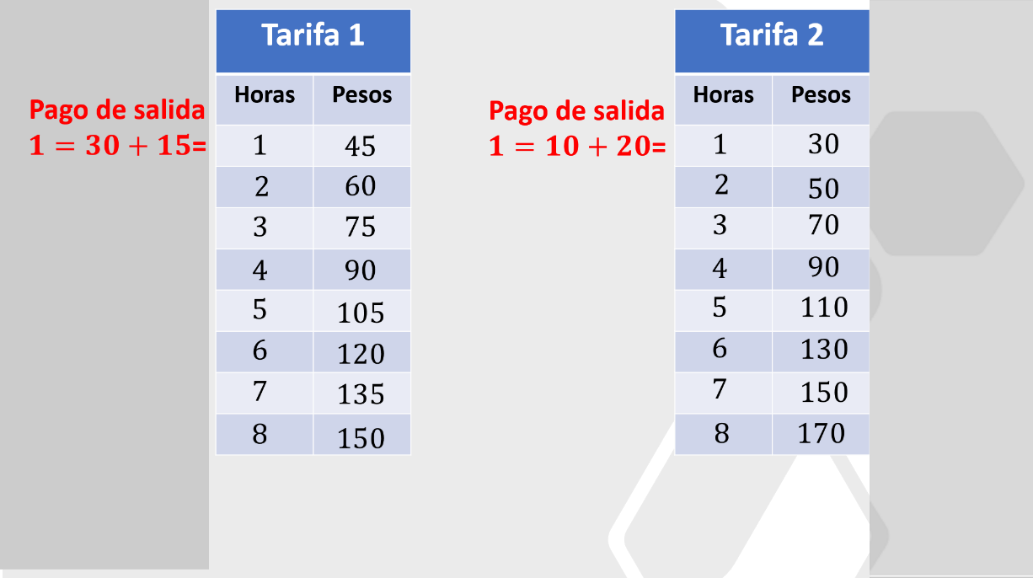
Algo similar ocurre con la tarifa 2, ya que también se debe dar un pago de salida, pero en este caso es de 10 pesos; así quedaría el pago de una hora: 10 pesos de salida más los 20 pesos de la renta.
Una vez generadas las tablas, puedes obtener la expresión algebraica de la variación lineal de cada situación.
Recuerda tus notas relevantes para obtenerla.

Traslada la tabla a una función para conocer la relación entre variables numéricas, las cuales algebraicamente puedes denominar como:
“x” y “y”
Es decir, a cada valor de “x” le corresponde un único valor de “y”.
Como puedes darte cuenta en la tabla de la tarifa 1, la razón de cambio es 15, ya que es el cociente de 2 cantidades que se relacionan.
En este caso, 15 entre 1, o bien con cualquier pareja de números, por ejemplo: 60 entre 4; 120 entre 8.
En todos los casos el resultado es el mismo: 15.
Si observas la tabla, puedes comprobar cada término, por ejemplo, si rentas 3 horas pagarías 45 pesos más los 30 de pago de salida, obteniendo así 75.
Recuerda que la forma de una variación lineal no proporcional es:
y = ax + b
Y para este caso:
y = 15x +30
15 es el valor que, multiplicado por el tiempo “x”, permite saber cuánto pagar por hora, a lo que se tienen que sumar los 30 pesos del pago de salida.
b = 30, ya que es el valor que se sumará al producto.
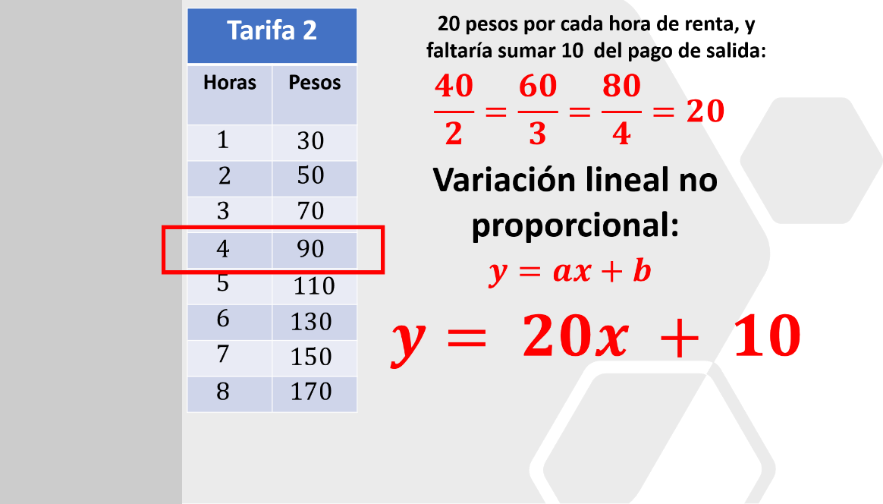
Para obtener la razón de cambio de la tarifa 2, hay que relacionar lo que se paga con el tiempo de uso, entonces:
Si rentas por 2 horas, pagarás 40, entonces 40 entre 2 = 20, por ejemplo, y si obtienes los cocientes faltantes te darás cuenta de que el resultado es el mismo: 20; esta es la razón de cambio.
Si observas la tabla, puedes comprobar cada término; por ejemplo, si rentas 4 horas, pagarías 80 pesos más los 10 de pago de salida, obteniendo así, 90.
Y la expresión algebraica sería:
y = 20(x) + 10
Donde el 10 se suma, ya que es el pago de salida por alquilar la bicicleta.
Con la tabulación y la expresión algebraica, puedes contestar cuál te conviene más en determinado tiempo.
Sin embargo, hay otra forma de analizar los datos; es decir, puedes graficar los datos para obtener un mejor análisis de la situación.
Retoma la tabulación, puedes obtener las coordenadas para poder graficar cada tarifa. Es importante colocar el título de la gráfica, que en este caso la llamarás “Pago contra tiempo”.
Cabe mencionar que las “x”, o eje de las abscisas, representan el tiempo en horas en este caso.
Y el eje “y”, de las ordenadas, el pago en este caso.
Trabaja en ubicar cada punto.
Para la tarifa 1:
x = 0, y = 30; este es el punto del pago de salida.
Para x = 1, y = 45
Para x = 2, y = 60
De la misma manera ubicas todos los puntos de la tabla y los unes con una línea recta.
Para la tarifa 2:
x = 0, y = 10; este es el punto del pago de salida.
Para x = 1, y = 30
Para x = 2, y = 50
De la misma manera ubicas todos los puntos de la tabla y éstos los unes con otra línea recta.
Nótese que se intersecan en el punto (4,90), y a partir de aquí se separan.
Recuerda esto para poder contestar las preguntas posteriormente.
Como puedes notar, obtienes líneas rectas en ambos casos. Además, ninguna recta pasa por el origen, por lo cual, se denominan variación lineal no proporcional con su forma:
y = ax + b
Donde “a” es la razón de cambio y la diferencia entre cada par de números de la columna de la “y”.
Y “b” es el valor en el eje de las “y” por donde cruza la línea.
Ahora sí, puedes contestar las preguntas iniciales del problema:
- ¿Cuál le conviene rentar si ocupa la bicicleta sólo 3 horas?
- ¿Y cuál lugar de renta le conviene a Omar si ocupa la bicicleta 8 horas?
Observa nuevamente la gráfica donde se comparan ambas tarifas y contesta.
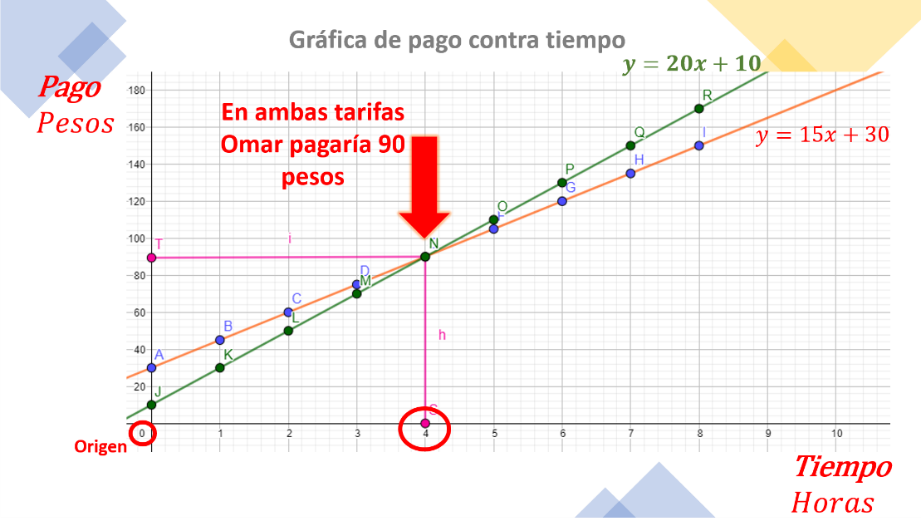
Como puedes observar en la gráfica de pago contra tiempo, ambas rectas coinciden cuando han pasado 4 horas de renta.
En ambas se pagarían, en total, 90 pesos, es decir, si Omar ocupa la bicicleta por ese lapso, cualquiera de las opciones es aceptable.
Ahora sí, para responder a las preguntas iniciales:
¿Cuál le conviene rentar si ocupa la bicicleta sólo 3 horas?
La tarifa 2, ya que pagaría 70 pesos, 5 pesos menos que la tarifa 1. Tal como se observa en la gráfica.
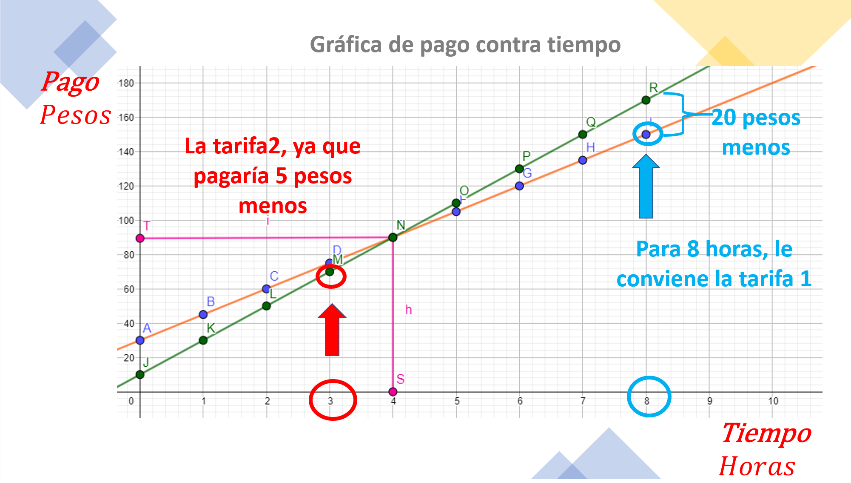
¿Y cuál le conviene si la ocupa 8 horas?
Para 8 horas le conviene la tarifa 1, pagando 150 pesos, 20 pesos menos que la tarifa 2.
Con el ejemplo de Omar, te puedes dar cuenta cómo la variación lineal puede ser también no proporcional.
No olvides poner en tus notas relevantes las características de la variación lineal no proporcional:
- La expresión algebraica es:
y = ax + b - Y tiene como gráfica una línea recta que no pasa por el origen (0,0) en el plano cartesiano.
El reto de hoy:
Recuerda que en tu libro de texto puedes localizar algunos ejemplos y secciones de apoyo para consolidar los aprendizajes.
En caso de que no cuentes con el libro de texto, tienes la opción de consultarlo a través de la página de la Comisión Nacional de Libros de Texto Gratuitos.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más: