Rectas y ángulos

Rectas y ángulos

(Clase de repaso)

Aprendizaje esperado: analiza la existencia y unicidad en la construcción de triángulos y cuadriláteros, y determina y usa criterios de congruencia de triángulos.

Énfasis: conocer las relaciones entre rectas paralelas cortadas por una transversal y los ángulos entre ellas, así como determinar las relaciones entre la suma de los ángulos de triángulos y cuadriláteros.

¿Qué vamos a aprender?

Hoy abordarás el tema de rectas y ángulos, y para eso te presentaremos un instrumento que anteriormente se usaba en arquitectura o bien en casa cuando se deseaba ampliar una imagen. Analizarás su diseño y te ayudará a estudiar algunos temas de geometría.

¿Qué hacemos?

El pantógrafo es un instrumento que se utiliza para hacer dibujos a escala. Examinarás las partes que lo conforman y que son determinantes para que el pantógrafo funcione:

Si observas con cuidado, al intersecarse las piezas de madera forman ángulos entre sí. Analiza esta parte del pantógrafo. Determina la cantidad de ángulos que se forman entre estas 2 piezas de madera.

Se forman en total 4 ángulos. ¿De qué manera podrías conocer la medida de estos ángulos?

Si tienes un pantógrafo en casa, utiliza un transportador para obtener las medidas de los ángulos. Ten cuidado de no mover el pantógrafo o la medida del ángulo cambiará. Si no cuentas con uno, traza con regla dos segmentos de recta que se corten en algún punto como los de la imagen que acabas de observar.

Toma como guía la siguiente imagen. Coloca tu transportador de manera que el centro corresponda con el ángulo que medirás. Identifica la medida que corresponde a la apertura y toma nota.

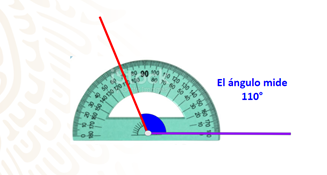
Con el transportador puedes visualizar que la medida del ángulo 1 es 110 grados. Continúa midiendo y observa que la medida del ángulo 2 es de 70 grados. El ángulo 3 mide 110 grados y el ángulo 4, 70 grados.

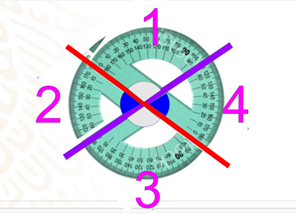
Hay una propiedad en los ángulos que se midieron. ¿Puedes observar que el ángulo 1 y el ángulo 3 miden lo mismo? De igual manera el ángulo 2 y el ángulo 4 miden lo mismo entre ellos.

Al intersecarse dos rectas, los ángulos opuestos que se forman son iguales, pues tienen la misma medida y se les conoce como “ángulos opuestos por el vértice”. Para entenderlo mejor, observa el siguiente video:

1. Ángulos opuestos por el vértice visual
   https://youtu.be/e5ZgFK_mWwY
   Centra tu atención en este par de piezas que se intersecan, observa cómo la medida del ángulo 1 y 3 aumenta o disminuye a la par; y por otro lado, sucede exactamente lo mismo con el ángulo 2 y 4.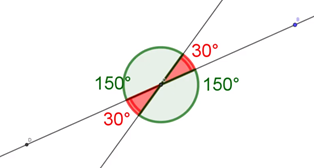
   
   
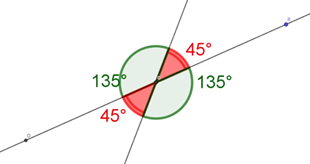
   Otro dato importante que puedes visualizar es que, el ángulo 1 y el ángulo 2 están uno junto al otro, por lo que reciben el nombre de: “ángulos adyacentes” y juntos forman un ángulo que mide 180 grados.
   Observa la siguiente imagen donde podrás visualizar la media vuelta del ángulo 1 y 2 juntos.
   
   La característica de este par de ángulos hace que reciban un nombre en especial: “ángulos suplementarios”, ya que si los sumas obtendrás 180 grados en total.
   Por lo tanto, estamos hablando de ángulos adyacentes suplementarios.
   Anota en tu cuaderno: qué pares de ángulos son adyacentes suplementarios y qué pares de ángulos son opuestos por el vértice.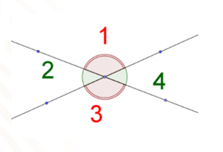
   
   Si prestaste atención tendrías la siguiente lista ordenada.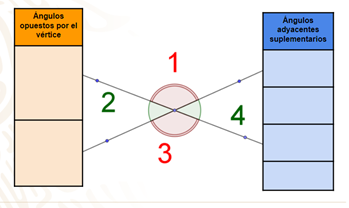
   
   Observa la siguiente imagen.
   
   Las dos barras al trasladarse al plano se pueden interpretar como rectas paralelas, ya que son equidistantes entre sí. Es decir, siempre mantienen la misma distancia entre ellas y aunque prolonguemos su trayectoria hasta el infinito nunca se cruzan. De ahí que reciban el nombre de: “Barras paralelas”.
   Las rectas paralelas modelan distintos objetos de nuestro entorno. Por ejemplo, en los parques puedes encontrar, con regularidad, un área en donde las personas realizan actividades físicas y hay barras paralelas en donde se puede hacer ejercicio para fortalecer los músculos del cuerpo.
   Como ya lo has visto, la geometría es una rama de las matemáticas y, entre muchas cosas, estudia a las rectas paralelas cuando son cortadas por una transversal. Al ser cortadas de esta manera forman 8 ángulos y podemos establecer una relación entre estos ángulos. Observa el siguiente video del minuto: 00:20 al 01:27, que te ayudará a fortalecer estos conocimientos.
2. Ángulos entre paralelas
   https://youtu.be/sCumX45DiaY
   Como confirmaste, gracias al video, cuando dos rectas paralelas son cortadas por una transversal se forman 8 ángulos y entre ellos puedes encontrar pares de ángulos iguales, pero ¿cuáles son estos ángulos y qué nombre reciben?
   
   Revisa la siguiente imagen y haz una relación con el pantógrafo con el que trabajaste anteriormente. Te presentamos dos segmentos de rectas paralelas en color rojo cortadas por una transversal, concéntrate en los ángulos 1 y 2, como puedes ver, el ángulo 1 es menor a 90 grados, se conoce como ángulo agudo, y en el ángulo 2 su apertura es mayor de 90 grados y se conoce como ángulo obtuso, según lo que acabas de estudiar, los ángulos 1 y 2 forman ángulos adyacentes suplementarios, ahora con los ángulos 2 y 4 se forman ángulos opuestos por el vértice.
   Ahora, analiza los ángulos que se forman dentro de los segmentos paralelos.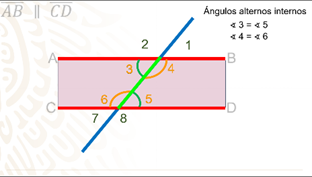
   
   Los ángulos 3, 4, 5 y 6 reciben el nombre de ángulos internos. Se llaman internos porque se encuentran entre las paralelas o en el espacio que está dentro de ellas. Con estos ángulos se pueden formar 2 pares de ángulos que son iguales entre sí y que reciben el nombre de alternos internos, alternos porque están en diferente lado de la transversal. Entonces, la primera pareja de ángulos que cumplen con esta condición son los ángulos 3 y 5; la segunda pareja son los ángulos 4 y 6. Y si observas detenidamente, te podrás dar cuenta de que tienen la misma apertura, esto significa que miden lo mismo.
   Hasta ahora, ya conoces tres tipos de ángulos: los adyacentes, los opuestos por el vértice y los alternos internos. Ahora, analizarás otro tipo de ángulos: los “ángulos alternos externos”.
   Al igual que los ángulos anteriores, son alternos porque se encuentran en diferente lado de la transversal; y se llaman externos porque se encuentran en la parte de afuera de las paralelas.
   La primer pareja de ángulos alternos externos que analizarás son los ángulos 1 y 7, la segunda pareja son los ángulos 2 y 8. Como puedes observar, también tiene la misma apertura, esto significa que miden lo mismo.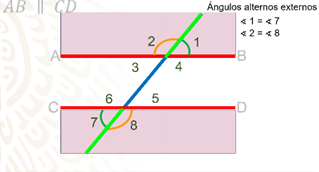
   
   Encuentra el último tipo de ángulo con el que trabajarás en esta sesión. Observa la siguiente imagen y trata de encontrar otra pareja de ángulos que sean iguales entre sí y que no haya sido mencionada anteriormente.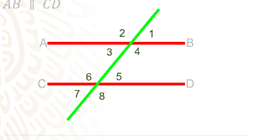
   
   Ese par de ángulos reciben el nombre de ángulos correspondientes, estos se encuentran del mismo lado de la transversal y del mismo lado de las paralelas; uno es interno y el otro es externo. Por ejemplo: el ángulo 3 está dentro de las paralelas, este es el ángulo interno y el ángulo externo que se encuentra de ese mismo lado de la transversal es el ángulo 7; entonces los ángulos 3 y 7 son correspondientes. Como puedes observar su apertura es igual, por lo tanto, miden lo mismo.
   Si observas detenidamente, podrás encontrar otros 3 pares de ángulos correspondientes entre las paralelas, que, por lo tanto, son iguales. El segundo par de ángulos son el 2 y 6; el tercero son 1 y 5; y el cuarto par de ángulos correspondientes son 4 y 8.
   
   Bien, ahora que ya sabes cómo identificar los ángulos adyacentes, opuestos por el vértice, los alternos internos, los alternos externos y los ángulos correspondientes. Toma tu cuaderno y anota el siguiente problema para resolverlo.
   En los ángulos que se forman entre 2 segmentos paralelos cortados por una transversal, el ángulo 1 mide 60 grados. ¿Cuánto miden los demás ángulos? Y, ¿cuáles son iguales?
   Como puedes ver en la imagen, sólo se tiene el ángulo 1, que mide 60 grados, y se pide determinar la medida de los demás. Para esto te apoyarás en las características de los ángulos que estudiaste. Comienza con los ángulos 1 y 3 que son opuestos por el vértice y que por lo tanto miden lo mismo, entonces el ángulo 3 también mide 60 grados.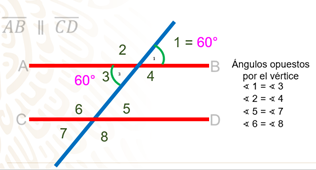
   
   Ya tienes el valor de los ángulos 1 y 3, ¿qué otro tipo de ángulos miden lo mismo que estos dos?
   Observa con atención. El ángulo 1 y el 3 miden lo mismo, porque son opuestos por el vértice. El ángulo 5, por ser ángulos alternos internos, entonces también mide 60 grados, el ángulo 7, por ser correspondientes. O bien, puedes argumentar que los ángulos 5 y 7 son opuestos por el vértice, por lo que el ángulo 7 mide 60 grados.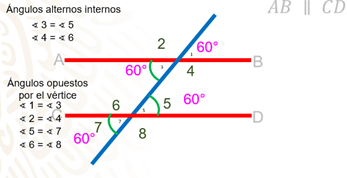
   
   ¿Cómo encontrarías el valor del ángulo 2?
   Para encontrar el valor del ángulo 2, puedes hacer uso de la característica de los ángulos adyacentes suplementarios. Sabes que estos ángulos juntos deben sumar 180 grados puedes realizar una sustracción para encontrar la medida de este ángulo.
   La diferencia de lo que valen los dos ángulos juntos, que es 180 grados, menos la medida del ángulo que conoces que es 60 grados y da como resultado 120 grados, por lo tanto, el ángulo 2 mide 120 grados.
   
   Te sugerimos concluir esta actividad. Puedes encontrar los valores de los ángulos entre dos paralelas cortadas por una transversal.
   Ahora te invitamos a que realices la siguiente actividad. Prepara lápiz, regla, tijeras y pegamento.
   En tu cuaderno, o en hojas reutilizables, traza un triángulo cualquiera. Ahora, con ayuda del siguiente video, sigue cada uno de los pasos que se indican.
3. Triángulo doble demostración suma de ángulos internos

https://youtu.be/D-zjDONVNf0

Sigue los siguientes pasos:

1. Coloca el triángulo en la posición de tu preferencia.
2. Con el lápiz indica que se hará un corte curvo punteando en dos de los vértices del triángulo.
3. Con las tijeras, corta cuidadosamente sobre la indicación punteada.
4. Ahora puedes manipular dos de los vértices del triángulo, pégalo usando pegamento escolar de manera consecutiva, junto al vértice que no cortaste, es decir, un vértice después del otro.

Observa detenidamente y trata de contestar las siguientes preguntas:

Al unir los vértices del triángulo de manera consecutiva. ¿Qué tipo de ángulo se forma?

¿Identificaste el ángulo llano?

La siguiente reflexión es: ¿A qué piensas que se deba la coincidencia? ¿Por qué observas el mismo tipo de ángulo? Al realizar la suma de la medida de los ángulos internos de un triángulo ¿qué medida se obtiene? Observa el siguiente video del minuto: 02:07 a 04:36que te ayudará a confirmar tu respuesta.

1. Los ángulos interiores de un triángulo

https://www.youtube.com/watch?v=Zr1UkSu_pE4

Como pudiste confirmar, la suma de la medida de los ángulos internos de un triángulo, siempre da como resultado 180º y en el video se presentan una manera distinta de comprobarlo, haciendo uso de las propiedades de los ángulos que se forman entre dos paralelas cortadas por una secante.

Considerando lo anterior, ¿cuál es la medida de cada uno de los ángulos internos de cualquier triángulo equilátero?

Durante la primaria, estudiaste las características de los triángulos, en este momento centrarás tu atención en los triángulos equiláteros, reciben ese nombre debido a que la medida de sus tres lados es la misma y otra característica con la que cuentan es que la medida de sus ángulos también es la misma. Por lo tanto, es sencillo calcular la medida exacta de sus ángulos internos.

Para confirmarlo hazlo con el planteamiento de una ecuación. Como ya sabes que la medida de los tres ángulos es la misma y la suma de ellos es igual a 180 grados, plantea la ecuación que representa esta situación, y para lograrlo, denotarás a cada uno de ellos con la literal “y”; de la siguiente manera: Puedes representar la medida de un ángulo como gustes; en esta ocasión con la “y”. Representando a la suma de las medidas de los 3 ángulos del triángulo equilátero, de la siguiente manera:

y+y+y = 180

Realiza la suma algebraica en el primer miembro de la ecuación y obtendrás:

3y = 180 grados.

Haciendo uso de las propiedades de la igualdad despeja “y” para conocer su valor, así que divide ambos miembros de la ecuación entre 3, y obtendrás:

3y/3 = 180 grados/3

Resuelve, 3y / 3 es igual a “1 y”. Recuerda que puedes no escribir el 1, eso es igual a dividir 180 grados entre 3, que da como resultado 60 grados; por lo tanto: y = 60 grados.

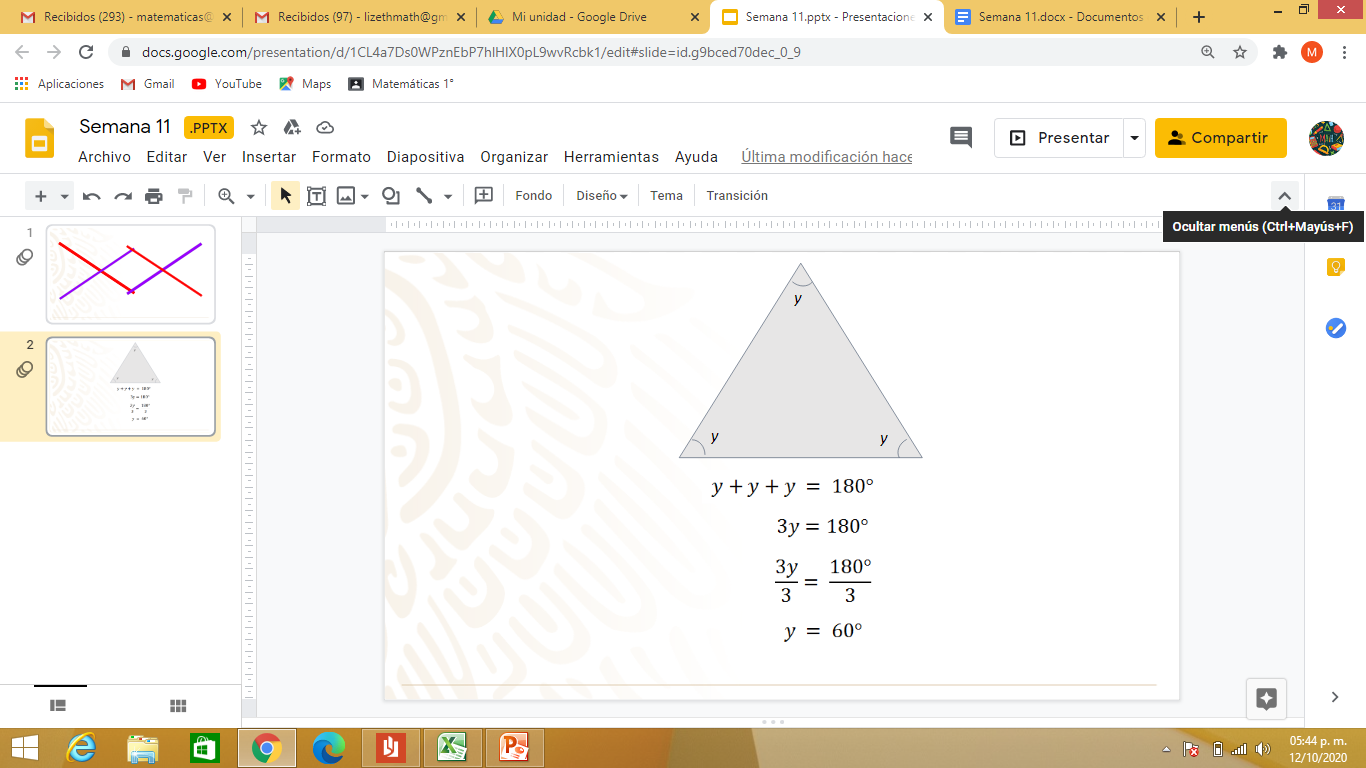
Bien, con el planteamiento de la ecuación, has observado que la medida de los ángulos internos de un triángulo equilátero es igual a 60 grados.

El reto de hoy:

Trabaja en tu cuaderno o en tus hojas de trabajo con el siguiente triángulo; plantea la ecuación que te ayudará a encontrar la medida de cada uno de sus ángulos. No olvides resolverla haciendo uso de las propiedades de la igualdad.

Puedes seguir los pasos que trabajaste anteriormente, diseña la igualdad que representa la suma de los tres lados y resuélvela, una vez que tengas el valor de la literal, sustituye en cada una de las expresiones que representan los vértices del triángulo.

Revisa en tu libro de texto el tema estudiado y realiza las actividades que ahí te sugieren.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/