¿Qué sigue?

Aprendizaje esperado: identifica y aplica la regularidad de sucesiones con números (naturales, fraccionarios o decimales) que tengan progresión aritmética o geométrica, así como sucesiones especiales. Construye sucesiones a partir de la regularidad.

Énfasis: construye sucesiones con progresión aritmética, geométrica y especial, a partir de la regla de formación.

¿Qué vamos a aprender?

Aprenderás sucesiones numéricas a partir de conocer su regla de formación. Cuando se hace referencia a sucesiones numéricas, se piensa en listas de números, por ejemplo, el número de lista que tienes, de registros de matrículas o placas de automóviles.

¿Qué hacemos?

Las sucesiones están implicadas en diversas situaciones, algunas sucesiones son muy famosas, en parte porque permiten, por ejemplo, describir y comprender aspectos de la naturaleza.

Las sucesiones de números son sencillas de entender y aplicar, como ocurre con la sucesión de números pares y con la lista de número de alumnos, por ejemplo.

Los números 2, 4, 6, 8, 10, 12, etcétera es una sucesión, cada uno de los números pares son elementos o términos de la sucesión. ¿Cuál es el número par que sigue después del 12? en efecto es el 14

Y luego, ¿Cuál término sigue? El 16

¿Cuáles son los dos términos que seguirían en esa sucesión de números pares?

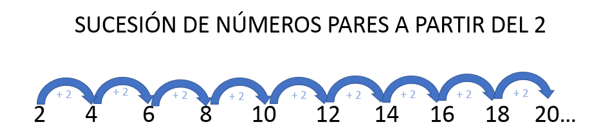
18, y 20 son los que siguen.

¿Cuál fue el primer término, es decir, con cuál número se inició la sucesión de números pares?

Con el dos.

Observa los primeros diez términos que forman la sucesión de números pares.

Una característica esencial de una sucesión es que sus términos siguen un orden. Lo que permite identificar cuál es la posición que ocupa cada término. Así que, ¿Cuál es el segundo número par, si el primer término es el dos?

El cuatro, y luego sigue el seis, el ocho, el diez, y así sucesivamente. El quinto término es el diez, el sexto término es el doce, y así hasta el veinte.

El décimo término en esta sucesión es el número veinte. Esto pudo ser diferente, ya que se podría haber iniciado la sucesión con el número 6 o con el número 10, en esos casos, aparece el veinte en otras posiciones, por ejemplo, si el primer término es el 10 ¿En cuál posición o lugar queda el 20?

Quedaría 10, 12, 14, 16, 18, 20, en este caso queda en la sexta posición. ¿Qué pasa entonces con el número dos, cuatro, seis y ocho? En este caso, no son parte de la sucesión porque está iniciando con el número diez, aunque sea una sucesión de números pares.

Otra característica de las sucesiones es que es importante señalar cuál es el inicio de una sucesión, es decir, se puede definir con qué término se inicia.

Es indispensable que conozcas que toda sucesión tiene una regla o patrón que la genera y se puede identificar entre los términos de la sucesión. Cuando comparas dos números consecutivos, puedes identificar qué pasó con el primero para llegar al segundo y debes analizar si eso mismo sucede para pasar del segundo al tercero y del tercero al cuarto, es decir, debes analizar si existe una regla o patrón de cambio entre ellos. Algunas reglas son más sencillas de determinar que otras, pero siempre que se trate de una sucesión, existe una regla y una vez que la conoces puedes identificar más términos de la sucesión.

Los términos que forman una sucesión, en ocasiones no tienen fin, estas sucesione se conocern como sucesiones infinitas y otras que sí tienen fin, se les llama sucesiones finitas, esa también es otra característica de las sucesiones. En este caso de la sucesión de números pares que inicia con el número dos y, de la cual, ya se tienen 10 términos, ¿De qué manera se determina cuál es el número que sigue de 20?

Suma dos unidades a 20

20 mas 2, da 22, mas dos, da 24, mas 2, da 26

En esta sucesión la regla consiste en sumar dos al término anterior para obtener el siguiente, o también se puede decir que, entre cada par de términos, la diferencia es 2 observa, doce menos diez es dos, esa regla aplica en ambos casos, tanto en la sucesión que inicia con dos como en la que inicia con diez.

Lo que puede generar otras sucesiones de números pares a partir de indicar cuál es el primer término de la sucesión.

También es importante que identifiques que dos sucesiones completamente diferentes pueden tener el mismo patrón, por ejemplo, si inicias con el 1 y le sumas 2 ¿Cuál será el siguiente término?

El 3

Y, si continúas esta sucesión con ese mismo patrón, ¿Cuáles serán los 5 términos siguientes?

El 5, 7, 9, 11, 13…

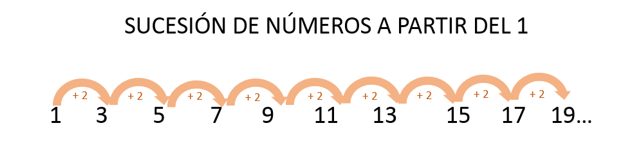
Observa que aunque el patrón sea el mismo, la sucesión es diferente porque se cambió el punto de partida.

Las sucesiones son listas o secuencias de números o figuras que presentan alguna regla de comportamiento.

Observa el ejemplo.

Hola, soy Emmanuel voy en sexto grado de primaria en la Escuela Defensores de la República. Quiero compartirles mi experiencia con el tema de las sucesiones. Tenía un poco de dificultad con este tema, pero pude analizar y contestar las preguntas que me hicieron sobre una sucesión y me siento tan contento que se las quiero compartir. Lo que me preguntaron fue:

En la sucesión de números decimales que inicia en 0.3 y llega hasta la unidad, se desea saber:

• ¿Cuánto se agrega entre cada término?
• Para llegar a la unidad a partir de 0.3 ¿Cuántos términos más forman la sucesión?
• ¿Cuántos términos en total forman la sucesión?
• ¿Cuál término ocupa la quinta posición?
• ¿Cuál es la posición del término 0.5?
• El número 0.75 ¿Es un término de la sucesión?

Es una sucesión que comienza en 0.3 y puedes observar cómo Emmanuel dividió un entero en décimos y ubicó los números de la sucesión, con esa estrategia pudo encontrar la respuesta a las preguntas que le hicieron.

Has observado una sucesión numérica cuyos términos son números decimales y también se ha mostrado una estrategia para encontrar la regla o patrón que existe entre ellos.

https://www.conaliteg.sep.gob.mx/

Ahora es momento de trabajar con los problemas que se plantean en el libro de texto, desafío 58, página 115 busca estrategias que te permitan comprender y resolver cada problema. Lee la consigna.

Pregunta 1. Si una sucesión aumenta de 1.5 en 1.5 ¿Cuáles son los primeros 10 términos, si el primero es 0.5?

Recuerda una sucesión, en particular numérica, es aquella lista de números que siguen una regla o patrón. En este caso para comprender la sucesión que se pide generar, vas a usar el dinero.

La sucesión comenzará con 50 centavos. Luego, cada día se ahorra $1 con 50 centavos, registra cuánto dinero tenía ahorrado al segundo día.

El segundo día tenía 2 pesos.

Al tercer día, ya tenía 3 pesos con 50 centavos, el cuarto día, 5 pesos, ¿Cuánto tendrá ahorrado a los 10 días? Apenas 10 pesos.

Esta sucesión es igual a la que piden en el primer desafío de la página 115

Con la única diferencia que ahí anotan 0.5 en lugar de 0.50 y 1.5 en lugar de 1.50 pero recuerda que, en el caso de los decimales, puedes eliminar los ceros que están a la derecha si es que no hay otra cifra diferente enseguida.

Ahora, revisa el problema dos.

¿Cuáles son los primeros 10 términos de una sucesión si el inicial es dos tercios y la diferencia entre dos términos consecutivos es un sexto?

Ahora deja los números decimales y pasa a las fracciones.

Recuerda que ya has trabajado con fracciones, sus equivalencias y significados.

Escribe las fracciones que te está solicitando.

Primero, identifica entre todos los datos que se tienen cuál es la regla que existe entre los términos de esta sucesión y cuál es el primer término.

La regla es que la diferencia de un término a otro es un sexto, es decir, aumenta un sexto entre el término anterior y el siguiente. Y la sucesión comienza con dos tercios.

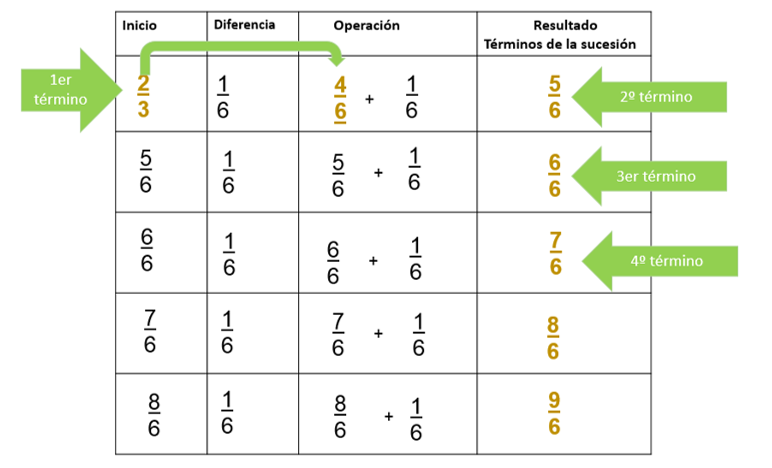
Se inicia con dos tercios y hay que aumentarle un sexto para obtener, el segundo término, entonces, ¿De qué manera se podría hacerlo?

Para facilitar la búsqueda de los términos siguientes, se puede convertir dos tercios en sextos.

Y dos tercios es equivalente a 4 sextos, así ya es más fácil sumar sextos con sextos.

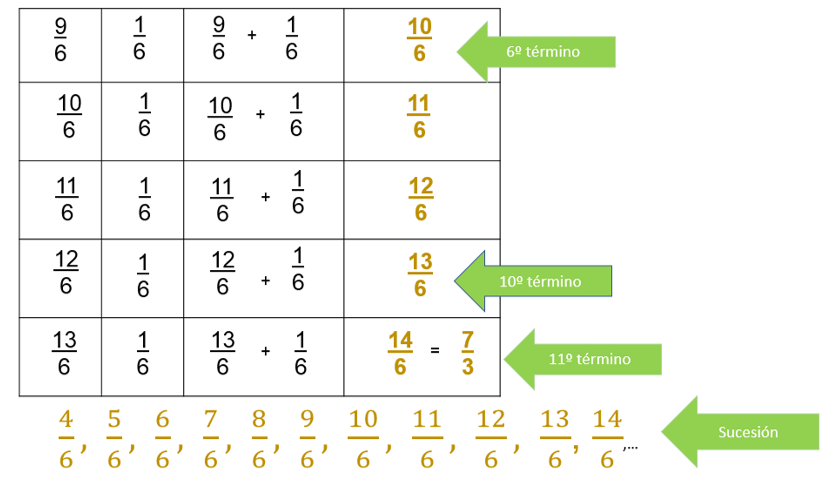
Observa la imagen donde se aparecen los 10 primeros términos de esta sucesión, y abajo se puede ver una sucesión equivalente a la anterior, expresada precisamente con términos equivalentes a los de la primera sucesión.

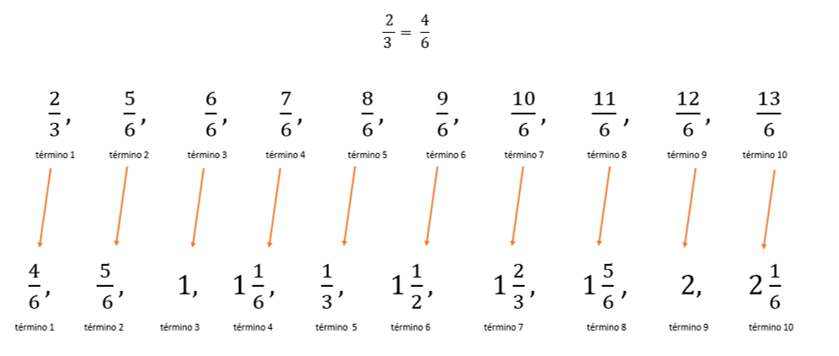
Todos los términos de la segunda sucesión son equivalentes a los que se obtuvieron en la primera sucesión.

Entre ellos existe el mismo patrón de crecimiento y el primer término es el mismo punto, sólo representado en forma diferente. Ahora analiza el crecimiento de estas figuras.

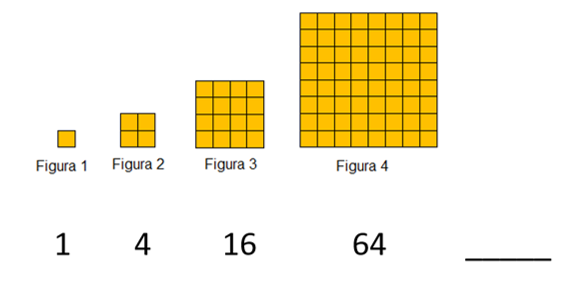
Observa que la primera figura tiene un cuadrado, la segunda tiene 4 cuadrados, la tercera tiene 16 cuadrados, y la cuarta tiene 8 de este lado y 8 de este, son 64 cuadrados.

Si anotas con números ese crecimiento obtendrás 1, 4, 16, 64 ¿Cuántos cuadrados tendrá la siguiente figura a ésta con 64 cuadritos?

Para pasar de un término a otro, se multiplica al anterior por 4, 1 por 4, es 4, 4 por 4, es 16, 16 por 4 es 64, entonces el siguiente será 64 por 4 y son 256. Y el siguiente tiene 1024 cuadritos, esta sucesión crece mucho.

Esta sucesión no es como las dos anteriores, esta crece mucho porque en lugar de sumar una cantidad constante, aquí el patrón es multiplicar por un número natural.

Aunque el número natural por el que se multiplica sea pequeño, el crecimiento es mucho mayor que cuando se suma, claro con excepción del uno, que al multiplicar no afectaría al término anterior.

Entonces se pueden encontrar sucesiones donde el patrón de crecimiento o regularidad consiste en sumar un número constante al anterior, para obtener el siguiente y otras donde la regularidad se encuentra multiplicando al número anterior por un número constante, como en esta última sucesión.

Son dos tipos de sucesiones diferentes.

Los números y sus relaciones son muy interesantes y puede resultar muy entretenido indagar acerca de ellos.

El reto de hoy:

Comparte el trabajo realizado con algún familiar y explícale como resolviste los ejercicios de tu libro de texto, seguramente le parecerán muy interesantes y útiles.

Si en tu casa hay libros relacionados con el tema, consúltalos, así podrás saber más.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://www.conaliteg.sep.gob.mx/