Proporción directa con constante decimal
Proporción directa con constante decimal
Aprendizaje esperado: calcula valores faltantes en problemas de proporcionalidad directa, con constante natural, fracción o decimal (incluyendo tablas de variación).
Énfasis: calcular valores faltantes en proporciones directas. Resolver problemas de proporcionalidad directa con constante decimal.
¿Qué vamos a aprender?
Trabajarás con problemas de proporcionalidad directa, con constante con número decimal. Así como tablas de variación.
Seguirás confirmando a través del planteamiento de algunas situaciones, que la utilidad de las nociones de la proporcionalidad directa forma parte de diversos temas de Matemáticas, y además de nuestra vida cotidiana.
¿Qué hacemos?
En la sesión anterior estudiaste problemas de proporcionalidad directa, utilizando una constante con número fraccionario o también llamada constante fraccionaria, en situaciones que se relacionan con la cantidad de azúcar que consumimos en ciertas bebidas.
Ahora ya sabes que las fracciones y los decimales están íntimamente ligados y que los números fraccionarios tienen su representación equivalente en números decimales. Esta se obtiene por diversos procedimientos, uno de ellos es dividir el numerador entre el denominador, por ejemplo, ya conoces que un cuarto puede ser representado de forma decimal como 0.25, ya que son equivalentes y esto se puede demostrar efectuando la división.
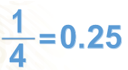
Este procedimiento ahora será útil para resolver problemas de variación proporcional directa con números decimales. Es probable que te preguntes: ¿cómo puedo completar una tabla de variación utilizando la constante de proporcionalidad con número decimal? Aquí encontrarás cómo hacerlo y podrás observar que el método es parecido al que realizaste en las lecciones pasadas.
Pon atención en lo que le pasó al Profesor Alejandro.

Ante esta situación y tomando como base las lecciones anteriores, ¿de qué manera puedes organizar la información? Efectivamente, con una tabla de datos o registro tabular, en tu cuaderno toma nota para poder dar respuesta a la pregunta de la situación planteada.
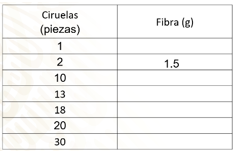
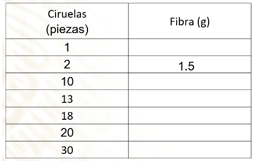
La tabla que se muestra tiene dos columnas, una correspondiente a la cantidad de piezas de ciruelas y la otra a la cantidad de gramos de fibra. En la primera fila se han escrito los títulos de la columna y la unidad de referencia. Por un lado, la cantidad de ciruelas y la segunda columna corresponde a los gramos de fibra que aportan las ciruelas.
En cada fila de la primera columna se ha registrado la cantidad de piezas de ciruelas que se consumen: 1, 2, 10, 13, 18, 20 y 30.
El uso de la tabla ayudará a establecer las relaciones entre los datos del planteamiento: al consumir 2 ciruelas, se consumen: 1.5 gramos de fibra, ¿cómo determinarías la cantidad de fibra que se ingiere al consumir 1, 10, 13, 18, 20 y 30 ciruelas?
Sabemos que el consumo de 2 piezas de ciruela provee 1.5 gramos de fibra, por lo tanto, ¿Cuánto provee de fibra el consumo de 1 pieza de ciruela?
Al apoyarnos con la tabla identificamos que para obtener la respuesta a la pregunta anterior podemos dividir 1.5 entre 2 que es igual a 0.75.
0.75 en este caso, representa la constante de proporcionalidad. Es decir, es el factor que, al multiplicarlo por las piezas de ciruelas, determina la cantidad en gramos de fibra que se ingiere, en correspondencia con las piezas de ciruela.

En este caso, para calcular la constante de proporcionalidad, que sabemos que es un mismo factor, se divide la cantidad en gramos de fibra que contienen las ciruelas, entre la cantidad de piezas de ciruelas.
Al modelar matemáticamente la situación, representaremos con la letra “y” (ye) a la cantidad de gramos de fibra que contienen las ciruelas, y representaremos con la letra “x”, a la cantidad de piezas de ciruelas.
Lo anterior se representa como:
k = y / x
Observa que la cantidad en gramos de fibra depende de cuántas piezas de ciruelas se ingieran; por lo que “x” representa la cantidad de ciruelas y “y” los gramos de fibra.
Ya que identificamos los datos necesarios para calcular la constante de proporcionalidad, determinemos su valor.

Vamos a sustituir los valores numéricos en la expresión general:
Sustituimos en “y” el valor numérico de la cantidad en gramos de fibra, cuando se consumen 2 piezas de ciruelas 1.5 y en lugar de “x” la cantidad de piezas de ciruelas que se consumen, que es 2.
Al resolver la operación obtenemos el valor de la constante K que es igual a 0.75.
Lo que quiere decir que por cada ciruela que consumamos obtenemos 0.75 gramos de fibra. Ahora con este dato podemos dar solución al problema planteado.

Veamos: En cada fila de la tabla habrá que multiplicar la cantidad de ciruelas por la constante de proporcionalidad, que también se representa como k:
Ya sabemos que, al consumir una ciruela, obtenemos 0.75 gramos de fibra. Enseguida multiplicamos 10 por 0.75, que es igual a 7.5, es decir, esto se interpreta como 75 gramos de fibra.
13 X 0.75 = 9.75, es decir, esto se interpreta como 9.75 gramos de fibra.
18 X 0.75 = 13.5, es decir, esto se interpreta como 13.5 gramos de fibra.
20 X 0.75 = 15, es decir, esto se interpreta como 15 gramos de fibra.
30 X 0.75 = 22.5, es decir, esto se interpreta como 22.5 gramos de fibra.

La interpretación en el contexto del problema es la siguiente:
por 1 ciruela tenemos 0.75 gramos de fibra,
por 2 ciruelas 1.5 gramos.
10 representan 7.5 gramos.
13 ciruelas aportan 9.75 gramos,
y así sucesivamente…
¿Sabías que la fibra que contienen las ciruelas previene enfermedades como la diabetes, el colesterol alto y el estreñimiento? Lo mejor es que esta fibra también se encuentra en la avena, las zanahorias, las manzanas y en muchos otros alimentos.
¿Sabías que tres manzanas aportan, aproximadamente, 12?96 gramos de fibra? si al día comieras una manzana. ¿Cuánta fibra te estará aportando al cuerpo?
Tenemos que tres manzanas, aportan 12.96 gramos de fibra, para encontrar la constante de proporcionalidad, dividimos 12.96 entre 3; lo que da como resultado 4.32.
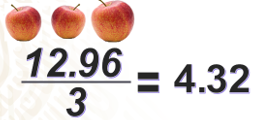
Por lo tanto, comer una manzana al día, aporta aproximadamente 4.32 gramos de fibra; ¡y mi nutriólogo me recomendó 25 gramos de fibra al día!
Seguramente otros conocimientos de las Matemáticas también se involucran en el cuidado de la salud, al poder calcular las porciones y la cantidad de alimentos que debemos comer; o bien, para saber cuáles de ellos es saludable consumir. Ya que, si necesitas consumir cierta cantidad de chayote –por el tipo de vitaminas que aporta-, por ejemplo, puedes sustituirlo por cierta cantidad de brócoli. Toma en cuenta que las medidas que trabajamos en los ejemplos anteriores son aproximadas, ya que existen distintos tipos de ciruelas y de manzanas, y cada fruta tiene distinto aporte nutricional; así que los datos pueden variar, lo ideal es que visites a una nutrióloga o a un nutriólogo, si tienes dudas sobre tu alimentación. Y podrás verificar que las personas especializadas en nutrición realizan operaciones y utilizan fórmulas matemáticas para poder elaborar una dieta con base en las necesidades de cada persona.
Buscando elementos relacionados con este tema, encontramos que en el uso de aparatos tecnológicos también se presentan situaciones que requieren del cálculo de la constante de proporcionalidad con números decimales, en situaciones de proporcionalidad directa. Pon atención a la siguiente situación:
Una amiga tiene una cámara profesional, que acaba de comprar para su trabajo como fotógrafa, con la que se dedica a tomar fotografías en eventos como bodas, cumpleaños y festivales. Al leer el instructivo, encontró que cada fotografía puede ocupar en la memoria de la cámara, desde 1.5 hasta 7 megabytes lo que quiere decir que en promedio puede ocupar 4.25 megabytes por fotografía.
Un megabyte es una unidad de medida de almacenamiento informático, utilizado comúnmente en computadoras, teléfonos celulares, internet, entre otras.
En tu cuaderno anota lo siguiente:

Con las especificaciones de la cámara donde calculamos que 1 fotografía consume aproximadamente 4.25 megabytes de memoria, completa la tabla. Ésta contiene en la primera columna la cantidad de fotografías, comienza con una, 10, después 25, 50, 75, 100 y 125. En la segunda columna anotaremos los Megabytes utilizados de acuerdo con la cantidad de fotografías. Una fotografía corresponde a 4.25 megabytes, en promedio, que es el valor que conocemos. Ahora responde a la pregunta:
Aproximadamente, ¿cuántas fotografías podrá tomar ella si la cámara tiene integrada una memoria de 500 megabytes?
En este caso como puedes observar, “x” representa a las fotografías y “y” son los megabytes que se ocupan en la cámara. Al establecer la razón, observamos que la constante, ya la conocíamos desde un inicio.
El resultado de dividir 4.25 entre 1 es 4.25, por ser el valor unitario, con este valor de la constante K ya podemos completar la tabla.

Para 10 fotografías multiplicamos 10 por la constante 4.25, el resultado es 42.5 megabytes. Continuamos, para 25 al multiplicar por la constante el resultado es 106.25 megabytes, así en 50 obtenemos 212.5, en 75 el resultado es 318.75 megabytes, para 100 tenemos la cantidad de 425 y con 125 fotografías se ocupan 531.25 megabytes de memoria.
Por lo tanto, no es posible tomar 125 fotografías ya que recuerda que la cámara tiene únicamente 500 megabytes de memoria interna.
Como ves, en este caso la constante de proporcionalidad es igual al valor unitario, o sea al tamaño que ocupa una sola fotografía. Pero aún nos falta saber: ¿Cuántas fotografías podríamos tomar con los 500 megabytes de la memoria interna?
Para obtener el resultado podemos hacer una comparación entre el tamaño total de almacenamiento, que son 500 megabytes, y entre el tamaño de cada fotografía, que es 4.25; y así obtener el resultado. Atención en lo siguiente:

Al hacer la comparación de 500 entre 4.25 el cociente es 117.64. Por lo que podemos responder que, podría tomar 117 fotografías; y quedaría un poco de espacio que no alcanzaría para hacer ni una fotografía más.
Es importante conocer este procedimiento ya que así podrás tener un mejor manejo de la cantidad de fotografías que puedes tomar. Para que todo esto quede más claro, observa al siguiente video:
- Proporcionalidad directa con constante con número decimal
Del minuto: 02:16 a 04:06
https://www.youtube.com/watch?v=oo20BdpMFuc
Analicemos otra situación:
Antonio es un chef que por una oferta de trabajo emigró a Canadá, ya que encontró un trabajo por medio de la Embajada de aquel país. Lo más significativo es que él lleva 3 meses viviendo allá y ha decidido guardar cierta cantidad de dinero para que a su regreso a México pueda poner su propio restaurante de comida típica mexicana. Hasta el momento ha podido ahorrar 4,374 dólares canadienses. ¿Cuánto dinero representa en pesos mexicanos, si en este día por 6 dólares canadienses, te devuelven 100.50 pesos mexicanos?
Comparado con el ejemplo del video nos damos cuenta que el tipo de cambio entre las monedas, de diferentes países, siempre es variable. Aunque podemos plantear una tabla de variación para darle seguimiento al incremento de su capital. Copia la tabla y completa obteniendo los datos por medio de la constante de proporcionalidad.
Trazamos la tabla con dos columnas, en los encabezados ponemos dólares canadienses y pesos mexicanos, debajo ocho filas con los valores para dólares canadienses de 1, 6, 18, 54, 162, 486, 1458 y 4374. En la columna de pesos mexicanos, en la fila del 6 anotamos 100.5 que es el valor en pesos mexicanos que nos está dando de referencia la situación analizada.
La variable dependiente “y” corresponde a los pesos mexicanos y la variable independiente son los dólares canadienses, ya que el dinero total que va a tener está en función de la cantidad de dólares que logre ahorrar.
Así tenemos que sustituir en la fórmula y obtenemos 100.5 entre 6.
Lo que resulta en 16.75, nuestra constante K.
Ahora, podemos fácilmente encontrar los valores faltantes de nuestra tabla multiplicando las cantidades de dólares canadienses por la constante K.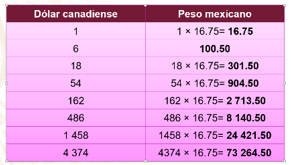
Por 1 dólar canadiense obtenemos 16.75 pesos mexicanos, por 18 dólares canadienses son 301.5 pesos; por 54 dólares tenemos 604.5 pesos, 162 dólares equivalen a 2 713.5 pesos; para 486 son 8 140.5; con 1 458 dólares tenemos 24 421.5 pesos, y por último 4 374 dólares canadienses se cambiarían por 73 264.5 pesos
Con la misma tabla encontramos la respuesta a la pregunta del problema, la cantidad de su ahorro en pesos mexicanos, en ese día es de $ 73,264.50. Recuerda que el tipo de cambio del peso mexicano con otras monedas, varía día con día.
Para continuar, observa al siguiente video del minuto: 00:14 a 02:09 - Proporcionalidad directa con constante con número decimal
https://www.youtube.com/watch?v=oo20BdpMFuc
De acuerdo con lo que observaste en el video, ¿cuánto nos cobrará el chofer si invitamos a 9 personas a Puerto Marqués?
Podemos encontrar los costos cuando conocemos la constante de proporcionalidad. Como pudiste observar en los ejemplos anteriores la proporcionalidad directa está presente en varias situaciones cotidianas y es muy común utilizarla sin que te des cuenta, tal y como lo puedes ver en el siguiente ejemplo:

¿Ya sabes qué hacer para ayudarle a Laura?
Al igual que en los ejemplos anteriores, lo primero será construir una tabla de variación, la cual queda de la siguiente manera: En la primera columna “Kilogramos de tortilla” y en la segunda “Precio en pesos”, el dato que ya tenemos es que se pagan 37.50 pesos por tres kilogramos de tortillas.
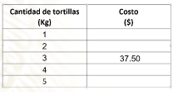
Seguramente ya sabes cuál es la variable independiente y la variable dependiente. El precio depende de cuántos kilogramos de tortilla se compren, por lo que el precio estará representado por la letra “y” y los kilogramos de tortilla por la letra “x”
Como ya lo sabes, ahora debemos calcular el cociente del precio entre la cantidad de kilogramos, es decir 37.5 entre 3, por lo que la constante de proporcionalidad es igual 12.5.

Ahora, sólo calculamos el producto de la cantidad de kilogramos de tortillas por la constante de proporcionalidad, y así encontraremos el precio por cada kilogramo que se quiera comprar:

Ahora Laura ya sabrá cómo obtener el precio de cada kilogramo de tortillas que le pidan:
Como lo observaste, la proporcionalidad directa es de gran utilidad ya que con ella podemos resolver una inmensa cantidad de problemas de distintas situaciones.
Ahora que ya trabajaste la constante de proporcionalidad directa con constante decimal en diversos contextos, no te olvides que para encontrarla se obtiene el cociente de la variable dependiente que está representada por la letra “y” entre la variable independiente que está representada por la letra “x”.
El reto de hoy:
Revisa en tu libro de texto el tema que estudiaste en esta sesión “Problemas de proporcionalidad directa”, y realiza las actividades que ahí se sugieren.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas