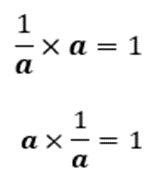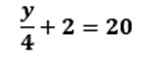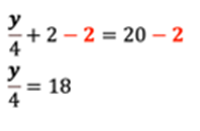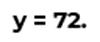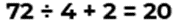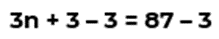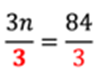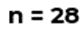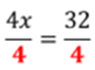Propiedades de la igualdad
Propiedades de la igualdad
Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de ecuaciones lineales.
Énfasis: aplicar las propiedades uniforme y transitiva de la igualdad.
¿Qué vamos a aprender?
En esta ocasión conocerás y aplicarás las propiedades de la igualdad, que te serán de utilidad para resolver ecuaciones de primer grado.
¿Qué hacemos?
Tal vez creas que nunca has visto nada de álgebra, pero sin darte cuenta, en muchas situaciones de la vida usas el álgebra sin llamarla así. Inclusive, resuelves problemas algebraicos de manera cotidiana.
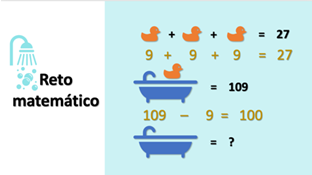
En distintos espacios virtuales, los retos matemáticos son cada vez más comunes, muchos de ellos usan imágenes que dan pistas para inferir valores desconocidos. Por ejemplo, la siguiente imagen representa un reto matemático similar a algunos de los que aparecen en las redes sociales. ¿Pueden encontrar el valor de la bañera, a partir de los iconos y la información matemática que aparecen en la imagen?
Es posible encontrar el valor de cada icono usando el álgebra. Y aunque aún no formalices ese proceso, lo puedes resolver con nociones algebraicas que has aprendido durante tu estudio de las matemáticas.
El pato de goma equivale a 9, porque 3 patos de goma equivalen a 27; ya que, el número que sumado por sí mismo 3 veces resultara 27 es 9. Ahora, la bañera con un pato de goma equivale al valor 109. Como ya se conoce que la equivalencia del pato es igual a 9, entonces sólo se debe obtener la diferencia entre el número 109 menos 9, que es igual a 100. Por lo tanto, la bañera equivale a 100.
Para saber más sobre esto, y resolver algunos ejemplos, observa el siguiente video del minuto 00:20 a 02:47:
- Ecuaciones a nuestro alrededor
https://youtu.be/0S7NOy08pe8
Las ecuaciones sirven para representar situaciones en las que se desconocen uno o más datos, y al resolverlas podemos encontrar dichos valores. Una ecuación se define como: una igualdad en la que aparece, al menos, una incógnita que se representa con letras, cuyo valor tenemos que encontrar, y en ella también se usan números y operaciones aritméticas. Aunque muchas veces las podemos resolver de manera mental, es importante desarrollar el procedimiento de solución por escrito. Así, cuando sean más complejas podrás resolverlas adecuadamente. En el ejemplo del video se menciona que, por 4 conchas, cuyo precio desconocemos, y un panqué de 25 pesos, se pagan 57 pesos. A partir de ahí se planteó la ecuación: 4x + 25 = 57.
Si te es posible, intenta resolver mentalmente esta ecuación, y anota el costo de cada concha en tu cuaderno, más adelante podrás verificar tu resultado.
Si una ecuación es una igualdad, podemos establecer que: la expresión matemática que se encuentra en un lado o miembro de la ecuación será equivalente a la expresión matemática que se encuentra en el otro lado o miembro de la ecuación. Estas expresiones pueden combinar operaciones aritméticas o algebraicas, es decir en las que aparezcan números y literales. Observa un ejemplo.
En la ecuación 5x + 10 = 15, el primer miembro de la ecuación, 5x + 10, es, por cierto, una expresión algebraica porque tiene una literal, en este caso “x”.
Lo que significa que, para que se cumpla la igualdad de la ecuación, el resultado o producto de 5 por “x” debe resultar 5, para que al sumarle el 10 que completa la expresión algebraica del primer miembro de la ecuación, sea igual a 15. Para que el producto 5 por “x” resulte 5, entonces “x” debe valer 1; así, 5 por 1 es 5, y luego al sumar el 10, resulta 15.
La igualdad tiene algunas propiedades que son de utilidad para resolver ecuaciones, vas a conocer sobre ellas para resolver ecuaciones de primer grado. Para resolver una ecuación se debe encontrar el valor de la incógnita, en este caso es la “x”.
Así que, el objetivo es despejar la incógnita “x”, lo que significa dejarla sola en uno de los miembros de la ecuación. Observa que el 10 también se encuentra en el primer miembro de la ecuación. Si restamos 10 en ese miembro, lograremos dejar sola a la “x”, pero también debemos hacerlo en el otro miembro de la ecuación. Así, obtenemos que 5x = 5.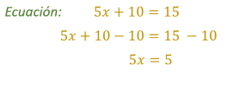
A esto se le conoce como “propiedad uniforme”, la cual establece que: si se aumenta o disminuye la misma cantidad en ambos miembros de la igualdad, ésta se conserva. Esto significa que, lo que se agregue o disminuya de un lado del signo igual, también se debe agregar o disminuir del otro.
Esta propiedad de la igualdad se resume a que las operaciones que se realicen en un miembro de la ecuación deben hacerse en el otro miembro de la ecuación también, para mantener la igualdad.
Desglosemos las operaciones de suma y resta; multiplicación y división. Así que, en ambos miembros de una ecuación se suma o resta la misma cantidad, para que la igualdad se conserve. Esto se expresa matemáticamente como:
Con la multiplicación y la división es algo similar. Así que, en ambos miembros de una ecuación se multiplica o divide la misma cantidad, para que la igualdad se conserve. Esto se expresa matemáticamente como: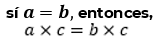
O bien, si tenemos: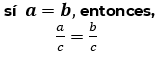
En el ejemplo se estableció que 5x es igual a 5. Para resolver la ecuación dividimos 5x entre 5, lo que resulta x. Pero debido a la propiedad uniforme, hacemos lo mismo en el otro miembro de la ecuación, por lo que dividimos 5 entre 5, lo que resulta 1. Así encontramos que x=1.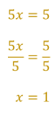
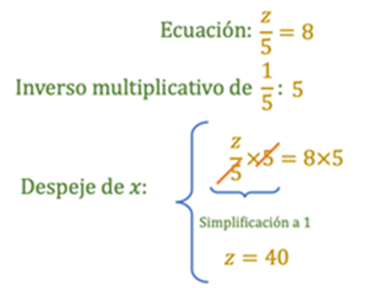
Esto significa que las operaciones que se hagan en un miembro de la ecuación, también se deben realizar en el otro miembro de la ecuación. Y hay algunas particularidades que observar. Se pueden usar el inverso aditivo y el inverso multiplicativo para hacer simplificaciones en las ecuaciones que ayuden a despejar las incógnitas.
Si se quiere simplificar a cero, se usa el inverso aditivo. Por ejemplo:
