Problemas de ecuaciones lineales
Problemas de ecuaciones lineales
Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de ecuaciones lineales.
Énfasis: plantear y resolver una ecuación a partir de un problema dado y viceversa.
¿Qué vamos a aprender?
En esta lección, ampliarás los conocimientos sobre cómo plantear y resolver una ecuación lineal de la forma ax + b = cx + d, a partir de un problema dado y viceversa.
Para esta sesión utilizarás:
- Cuaderno de Matemáticas o en su defecto hojas reutilizables para tomar notas.
- Lápiz, goma, sacapuntas y
- Tu libro de texto de Matemáticas de primer grado.
En esta sesión darás continuidad al tema, solución de ecuaciones de la forma “ax + b = cx + d”.
Debes recordar que una igualdad es la equivalencia entre dos expresiones algebraicas relacionadas, a través del signo igual.
¿Qué hacemos?
Antes de iniciar con el tema de hoy, te invito a resolver el siguiente reto:
Observa las operaciones de figuras y números:
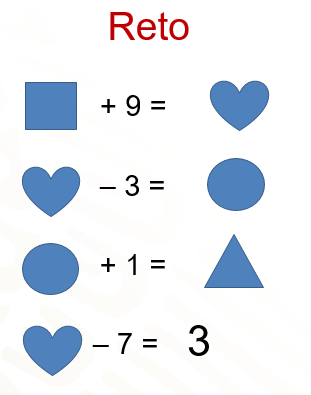
Un cuadrado más 9 es igual a un corazón.
El mismo corazón menos 3 es igual a un círculo; a su vez, el círculo más uno es igual al triángulo y finalmente, el corazón menos 7 es igual a 3.
El reto consiste en encontrar el valor que representa cada figura, de manera que se cumplan todas las igualdades.
Al final de esta sesión se dará respuesta a este reto.
Comienza analizando la siguiente situación:
“Martha y Alberto tenían la misma cantidad de dinero y compraron lápices del mismo precio. Martha compró 5 lápices y le quedaron $15.00 y Alberto compró 3 lápices y le sobraron $29.00. ¿Cuánto cuesta cada lápiz?
Iniciemos por traducir la situación al lenguaje algebraico. Nuestra incógnita, que es el costo de cada lápiz, la representamos con la letra “x”. Por lo que, para el caso de Martha la expresión algebraica es: 5x + 15, se realiza una suma, porque 15 pesos es lo que le quedó en dinero.”
Para el caso de Alberto la expresión algebraica es: 3x + 29.
Como ambos tenían la misma cantidad de dinero, ahora igualas ambas expresiones para formar la ecuación que represente la situación, que es:
5x + 15 = 3x + 29
Observa que la ecuación representa una igualdad, por lo tanto, lo que haces de un lado, ya sea sumar, restar, multiplicar o dividir, tienes que hacerlo del otro lado, para conservar la igualdad.
Empieza a despejar la incógnita “x”; para ello, vas a utilizar el inverso aditivo. Recuerda que el inverso aditivo de un número es su opuesto, de tal manera que, al sumarlos, se obtiene cero. En este caso, para eliminar a la incógnita del lado derecho, sumarás 3x negativo en ambos lados, obteniendo:

5x + (-3x) + 15 = 3x + (-3x) + 29, reduciendo términos semejantes queda: 2x + 15 = 29.
Ahora, en el primer miembro de la ecuación, el término que tiene a la incógnita se está sumando con 15. Para lograr que la incógnita quede sola, se debe restar primero 15 en ambos miembros de la ecuación o se suma el inverso aditivo de 15, que es 15 negativo, de la siguiente manera:
2x + 15 +(-15) = 29 +(-15).
Ahora, simplifica y obtienes la ecuación:
2x = 14.
Como el coeficiente 2 está multiplicando a “x”, se multiplica por el inverso multiplicativo de 2 en ambos miembros de la ecuación que es un medio, o bien, se divide entre 2. De ahí obtienes 2x entre 2 es igual a 14 entre 2. Al resolver, se sabe que “x” es igual a 7; es decir, cada lápiz cuesta 7 pesos.
A partir de los resultados obtenidos, ¿puedes saber cuánto dinero tenían Martha y Alberto?
Al comprobar la solución de la ecuación, puedes responder la pregunta.
Si sustituyes a la incógnita por el valor encontrado en la ecuación inicial: 5x+15=3x+29, se tiene que 5 por 7 + 15 igual 3 por 7 más 29; al aplicar la jerarquía de las operaciones, se tiene: 35 + 15 = 21 + 29. Al simplificar ambos lados de la igualdad, se tiene 50 es igual a 50.

Queda comprobado que 7 es el número que satisface a la ecuación. Y con esto, puedes responder la pregunta, ¿cuánto dinero tenían Martha y Alberto?
La respuesta es que cada uno tenía 50 pesos.
Como te pudiste cuenta, puedes resolver ecuaciones en situaciones cotidianas y con más frecuencia de lo que te das cuenta.
Observa otra situación que te permita utilizar ecuaciones de primer grado.
“Patricia y Carmen son dos amigas que decidieron guardar sus ahorros, cada una en una alcancía que se habían ganado en una feria. Se pusieron de acuerdo y decidieron ahorrar una cantidad fija mínima, cada semana; pero, si querían, podían ahorrar un poco más. Empezaron a ahorrar en diferentes momentos, hasta la semana 5 tenían los siguientes ahorros:
Carmen ahorró, cada semana, durante 2 semanas, 8 cuotas fijas más 5 pesos. Y Patricia ahorró, cada semana, durante 5 semanas, 3 cuotas fijas más 4 pesos.
Si tienen los mismos ahorros, ¿qué cantidad acordaron ahorrar como cuota fija semanal? ¿Cuánto dinero han ahorrado?”
¿Qué es lo primero que tienes que hacer para saber cuánto dinero ahorraron Patricia y Carmen?
Lo primero que harás, es traducir a lenguaje algebraico la información, con una ecuación de la forma “ax + b = cx + d”.
Representa a la cuota fija de ahorro semanal con la letra “c”. La representación algebraica de esta situación queda: Carmen, 2 veces, 8 cuotas fijas más 5 pesos. Algebraicamente es: 2 por la suma 8c + 5. Patricia, 5 veces, 3 cuotas fijas más 4 pesos, que algebraicamente es: 5 por la suma 8c + 4. Al igualar las expresiones, obtenemos la ecuación: 2 por la suma (8c + 5) igual a 5 por la suma (3c + 4).

Como puedes observar, obtuviste una ecuación que incluye paréntesis; así que, lo primero que harás, será aplicar la propiedad distributiva, que dice que: la multiplicación de un número por una suma, es igual a la suma de las multiplicaciones, de dicho número, por cada uno de los sumandos
Para despejar a la incógnita “c”, primero multiplica 2 por 8c y 2 por 5 y 5 por 3c y 5 por 4, obteniendo la ecuación: 16c +10 = 15c + 20.

Ya que eliminas los paréntesis, aplicas el procedimiento visto antes para despejar a la incógnita. Sumarás el inverso aditivo de 10, en ambos lados de la ecuación, quedando: 16c+10 +(-10) = 15c +20 + (-10). Reduciendo términos semejantes obtienes: 16c = 15c + 10; ahora, sumas en ambos lados el inverso aditivo de 15c, para dejar a la incógnita de un solo lado de la igualdad, resultando: 16c + 15c negativo = 15c + 15c negativo + 10, reduce términos semejantes, nuevamente, lo que da como resultado c = 10.
Con esto, obtienes la solución de la ecuación y se concluye que la cuota que fijaron Patricia y Carmen fue de 10 pesos semanales.
¿Cómo puedes saber qué cantidad ha ahorrado cada una?
Lo primero que tienes que hacer es comprobar el resultado de la ecuación, que es el último paso en el procedimiento; y con esto, puedes saber la cantidad que cada una tiene ahorrado.
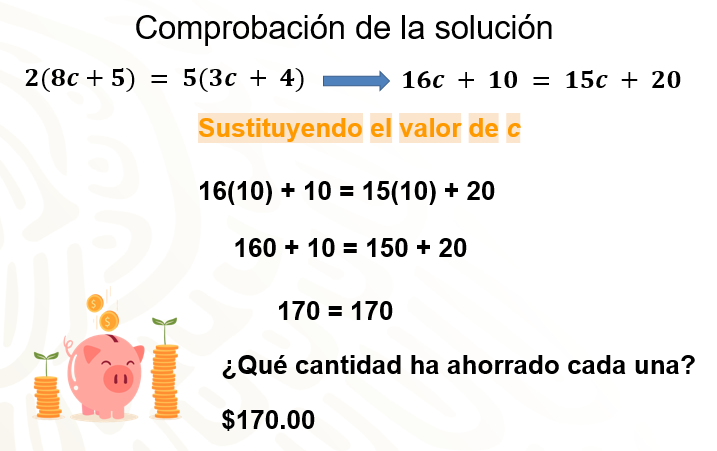
Observa, sustituyes el valor que se encontró para “c”, en la ecuación que obtuviste al aplicar la propiedad distributiva: 16c + 10 = 15c + 20, como c = 10, entonces: 16 por 10 más 10 es igual a 15 por 10 más 20. Resuelve las multiplicaciones y obtienes la igualdad: 160 más 10 igual a 150 más 20. Al simplificar, nos queda que 170 es igual a 170; por lo que la solución es correcta. Ahora ya sabes que cada una tiene ahorrados 170 pesos.
Ahora, resuelve la siguiente ecuación de la forma ax + b = cx + d.
El reto para ti será plantear un problema que se resuelva con dicha ecuación, que es:
3.5x + 8 = 6.5x – 4.
¿Qué situación-problema podría relacionarse con esta ecuación?
“La edad de Luis es igual a 3.5 veces la edad de Eduardo, más 8. pero también, la edad de Luis también es igual a 6.5 veces la edad de Eduardo, más 4 años: es decir, Si la edad de Luis es “x”; entonces, 3.5x + 8 = 6.5x – 4.”
Así se tiene que el problema cumple con la ecuación dada.
Ahora, habría que resolverla para conocer la edad de Luis y de Eduardo.
¿Recuerdas qué es lo primero que hay que hacer?
Se tiene que despejar la incógnita en uno de los miembros de la igualdad; en este caso, lo harás del lado derecho. Primero, como a 6.5x se le restan 4; entonces, sumas 4 en ambos lados de la igualdad, obteniendo la ecuación: 3.5x + 8 + 4 = 6.5x – 4 + 4, que al simplificar queda: 3.5x + 12 = 6.5x.
Ahora, se resta 3.5x en ambos lados para tener a la incógnita únicamente del lado derecho, 3.5x + 12 – 3.5x = 6.5x – 3.5x, al simplificar queda: 12 = 3x
Finalmente, para despejar la incógnita se divide entre 3 a ambos miembros de la ecuación.
Quedando 12/3 igual a 4 y 3x entre 3 igual a x, dando como resultado 4 igual a x o lo que es lo mismo aplicando la propiedad reflexiva o simétrica x es igual a 4.

Ya se tiene la solución de la ecuación y se sabe que la edad de Luis es de 4 años.
Pero, como en toda ecuación, se tiene que comprobar la solución del problema, lo que te permitirá conocer la edad de Eduardo.
En casa, comprueba la solución de la ecuación y comprueba que Eduardo tiene 22 años.
Para ahondar en la resolución de problemas que llevan a ecuaciones de la forma antes mencionada, analiza y resuelve la siguiente situación.
Se tiene la ecuación 10x – 5 + 3x – 6 = 10x + 10. ¿Qué observas en esta ecuación?
Para poder desarrollar todo el proceso ya conocido, primero se deben de reducir los términos semejantes del lado izquierdo de la igualdad, obteniendo 10 x + 3x = 13x y resuelve las restas de 5 y 6 obtienes a 11 como sustraendo. Muy bien, ahora ya tienes la ecuación de la forma que has trabajado en esta sesión: 13x – 11 = 10x + 10
Ahora puedes iniciar el despeje de nuestra incógnita en uno de los lados de la igualdad. Como a 13x se le resta 11; entonces, se suma 11 en ambos lados de la igualdad, obteniendo la expresión: 13x – 11 + 11 = 10x + 10 + 11, que al simplificar queda como: 13x = 10x + 21.
Ahora, se resta 10x en ambos lados para tener al término que tiene a la incógnita únicamente del lado izquierdo: 13x – 10x = 10x + 21 – 10x, que, al simplificar, queda como: 3x = 21.
Por último, para despejar la incógnita, se divide entre 3 a ambos miembros de la ecuación, resultando que “x” es igual a 7.

Una vez que se ha encontrado el valor de la incógnita “x”, se comprueba que el valor obtenido es correcto en la ecuación inicial:
10x – 5 + 3x – 6 = 10x + 10
Al sustituir el valor que se obtuvo de la “x”, se tiene que: 10 (7) – 5 + 3 (7) – 6 = 10 (7) + 10
Se realiza la operación en el miembro izquierdo y se obtiene:
70 – 5 + 21 – 6 = 80
Al efectuar las operaciones en el miembro derecho se tiene que: 70 + 10 = 80
Por lo que se obtiene finalmente que 80 = 80

Resuelve la siguiente situación problema:
La edad de Antonio es el doble de la edad de Ramiro.
Dentro de 6 años la edad de Antonio será 5/3 la edad de Ramiro.
La pregunta es: ¿Cuáles es la edad actual de ambos?
Iniciemos planteando la ecuación. Si la edad actual de Ramiro la presentamos con “x”; entonces, la edad de Antonio es 2x.
Dentro de 6 años la edad de Ramiro será x + 6 y la de Antonio 2x + 6. Como sabemos que en seis años la edad de Ramiro será 5/3 la edad de Antonio; entonces, se plantea la ecuación: 2x + 6 = 5/3 por (x + 6)

Si observas, la expresión tiene una fracción en el miembro derecho. Como es más práctico operar con números enteros, multiplicas ambos miembros de la ecuación por 3.
Y queda la ecuación: 3 por el binomio 2x + 6, igual a 3 por 5/3, por el binomio x + 6; como 3 por 5/3, es igual a 5, la siguiente ecuación que se obtiene es: 6x + 18 = 5 por el binomio x + 6. Al eliminar los paréntesis, tienes que: 6x + 18 es igual a 5x + 30.
Ahora, restas 5x en ambos miembros de la ecuación, para lograr que la incógnita esté únicamente del lado izquierdo: 6x + 18 – 5x = 5x + 30 – 5x. Simplificando se obtiene x + 18 = 30. El siguiente paso es restar 18 en ambos miembros de la ecuación, para que los términos independientes o constantes se encuentren sólo del lado derecho: x + 18 – 18 = 30 – 18, reduciendo se tiene x = 12;
¿Recuerdas qué representa a “x”?

Para poder saber las edades de Ramiro y de Antonio, sustituyes el valor de la incógnita x encontrada en la expresión algebraica.
Ramiro tiene 12 años y Antonio, 12 por 2, igual a 24 años y, dentro de seis años, Ramiro tendrá 12 más 6 igual a 18 años y Ramiro 24 más 6 igual a 30 años.
Con esto se demuestra que en 6 años la edad de Ramiro será 5/3 la edad de Antonio, ya que 30 es 5/3 de 18.
Observa la última situación problema.
Un recipiente tiene una cierta cantidad x en litros de agua. Si se le añaden 160 litros de agua tendría la miasma cantidad total en litros de agua que si a esa cierta cantidad x se le añadieran 10 litros y se triplicara.
¿Cuántos litros de agua hay en el recipiente?
¿Cuál es esa cantidad inicial de agua en el recipiente?
¿Lo tienes?, ¿Ya sabes cuál es la ecuación que representa a este problema?
En este caso, se desconoce la cantidad en litros inicial de agua que contiene el tanque, por lo que este dato será la incógnita a encontrar. Nuevamente, la se expresará con la literal “x”, obteniendo la ecuación:
x más 160 litros es igual a el triple del binomio x más 10, es decir, x + 160 = 3(x + 10).
Si observas tienes que emplear del lado derecho la propiedad distributiva para eliminar los paréntesis. Se multiplica el 3 por x y 3 por 10, al resolver tienes la ecuación: x + 160 = 3x + 30.
Ahora, se procede a despejar la incógnita “x”. En este caso, lo harás del lado derecho, entonces, en ambos lados de la igualdad restas x, y nos queda:
x + 160 – x = 3x + 30 – x, que al simplificar se obtiene:
160 = 2x +30.
Ahora, se restan 30 en ambos de la igualdad, 160 – 30 = 2x + 30 – 30, simplificando da: 130 = 2x.

Finalmente, para despejar la incógnita y encontrar su valor, se divide entre 2 ambos miembros de la ecuación, resultando que: 130 entre 2 = 2x entre 2, lo que da “x” igual a 65.
Ahora, ya puedes dar respuesta al cuestionamiento ¿Cuál es esa cantidad inicial x de agua en el recipiente?
La respuesta es 65 litros.
Y ¿Cuántos litros de agua hay en el recipiente?
Hay 65 más los 160 litros que se agregaron, es decir 225 litros.
En casa, comprueba que el resultado es el correcto sustituyendo a “x” por el valor obtenido y resolviendo las operaciones. Si tienes oportunidad, comparte con tu maestra o maestro tus resultados.
¿Qué te parece si, antes de terminar esta sesión, te das un momento para anotar lo más importante del tema que desarrollaste el día de hoy? Realiza en tu cuaderno tus anotaciones.
Recuerda que en la solución de ecuaciones se debe tener en cuenta lo siguiente:
- Leer detenidamente para comprender la situación que se plantea.
- Traducir el problema al lenguaje algebraico.
- Resolver la ecuación empleando la propiedad uniforme de la igualdad; es decir, encontrar el valor de la incógnita.
- Realizar la comprobación de la solución.
- Dar respuesta a los cuestionamientos de la situación problema, si es que existiera.
Es importante no omitir algún paso mencionado anteriormente; de esta manera, obtendrás un aprendizaje certero y un resultado algebraico correcto.
El reto de hoy:
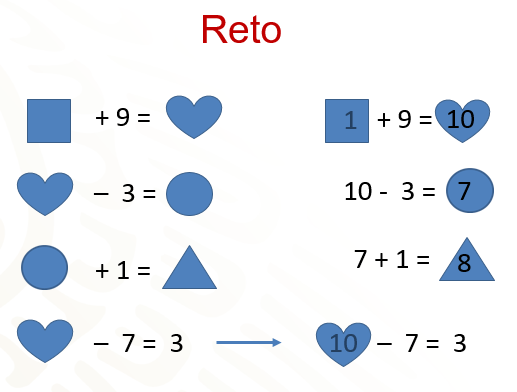
Si observas las operaciones, la cuarta nos indica que el resultado es 3; por lo que puedes considerar al corazón como la incógnita de una ecuación, entonces, sumas 7 en ambos lados y el resultado es corazón igual a 10. Ya tienes el primer valor de las figuras.
Conociendo el valor del corazón, ya puedes resolver la primera operación, cuadrado más 9, igual a corazón, es decir a 10; entonces, el número sumado con 9 da como resultado 10, es el 1. Entonces, el cuadrado vale 1.
La segunda operación indica el corazón menos 3 igual a círculo, como ya conoces el valor del corazón sustituyes su valor quedando 10 – 3 = a círculo. Al realizar la operación, obtienes 7, que es el valor del círculo. Vas por la última operación: círculo más 1 es igual a triángulo. Nuevamente, sustituyes el valor de círculo, que es 7, más 1, es igual a 8. El triángulo tiene como valor 8.
¿Qué tal? ¿Ya tenías las respuestas? Seguramente lograste obtener el mismo resultado.
En caso de que tengas dudas o deseen profundizar, te recomiendo apoyarte en tu libro de texto de Matemáticas de primer grado: o bien, volver a ver esta lección.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas