Problemas con números positivos y negativos
Problemas con números positivos y negativos
Aprendizaje esperado: resuelve problemas de suma y resta con números naturales, fracciones y decimales positivos y negativos.
Énfasis: resolver problemas de suma y resta de números positivos y negativos enteros, fraccionarios y decimales.
¿Qué vamos a aprender?
Realizarás cálculos matemáticos que te permitirán resolver problemas que se presentan en situaciones cotidianas, ya sea como cuando sales de la ciudad, cuando vas de compras o incluso cuando preparas tu comida favorita, verás que la suma y resta de números enteros, fraccionarios y decimales, positivos y negativos, se aplica en todas partes.
¿Qué hacemos?
Ya en sesiones previas has trabajado con operaciones de adición y sustracción de números positivos y negativos, tanto enteros como fracciones y números decimales.
Para recuperar tus conocimientos al respecto, se te invita a ver el siguiente audiovisual. Si tienes oportunidad, toma nota de lo que consideres importante para recordar.
- ¿Cómo sumar y restar números fraccionarios y decimales con signo?
https://www.youtube.com/watch?v=ishwQ7v9W6o
Revisa del tiempo 00:45 al 03:27.
Como pudiste observar en el video, es importante destacar que cuando se suman una cantidad positiva y otra negativa se calcula la diferencia entre los valores absolutos y al resultado se le da el signo del número que tiene el mayor valor absoluto.
Así como el problema visto en el audiovisual, a lo largo de la sesión resolverás distintos problemas de los cuales podrás ir verificando los resultados. Se te invita a tomar nota de la información de cada situación propuesta y a que intentes resolver lo que se te plantea.
Ahora que has leído el problema es momento de definir los datos y la operación que se tiene que realizar. Para saber la distancia a la que se encuentra el cangrejo respecto al nivel del mar, resuelve una suma de un número negativo más un número positivo:
¾ negativo más 9/8 positivo.
Al aplicar la regla de la adición, calcula la diferencia entre los valores absolutos de ¾ y 9/8.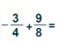
Observa que la fracción 9/8 tiene mayor valor absoluto que la fracción ¾ negativo, por lo que se puede anticipar que el resultado será positivo.
Hay que resolver la operación.
Para resolver la suma, primero se convierte las fracciones en fracciones equivalentes con igual denominador, que en este caso serán octavos.
Multiplica 3 por 2 y 4 por 2 para obtener la fracción 6/8 negativo.
Así quedara la suma 6/8 negativo más 9/8, para resolverla se calcula la diferencia entre los valores absolutos, que en este caso es igual a 3/8.
Entonces, el resultado de la suma 6/8 negativo más 9/8 es igual a 3/8, que como viste antes, el resultado es un número positivo porque 9/8 tiene mayor valor absoluto.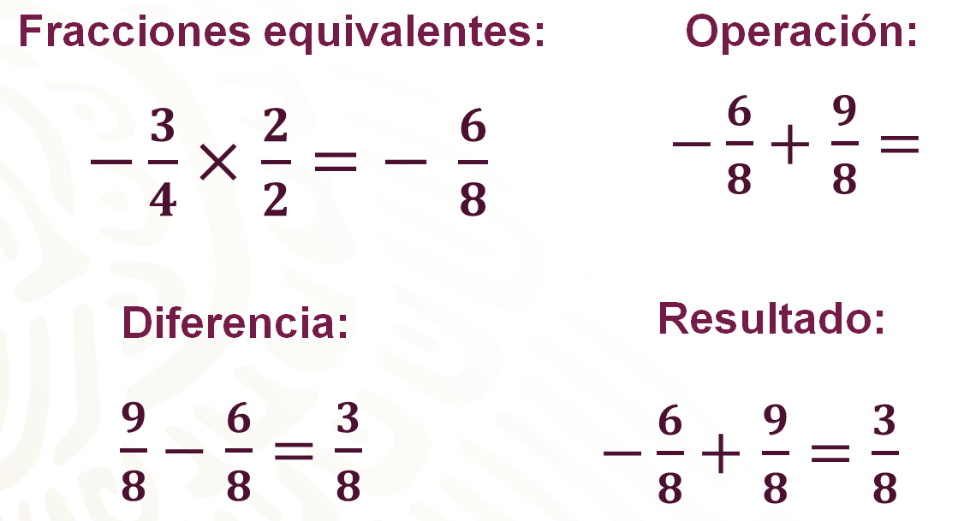
Así se puede concluir que el cangrejo subió sobre la roca una distancia de ⅜ de metro sobre el nivel del mar.
La fracción resultante en el problema de la tortuga es un número negativo e indicó que la tortuga se encontraba bajo el nivel del mar mientras que la fracción resultante del problema del cangrejo es un número positivo, lo que indica que el cangrejo está por arriba del nivel del mar.
Por ahora has resuelto problemas que implican la suma de fracciones positivas y negativas.
Ahora, sabiendo que la tortuga se encontraba a 27/40 de metro bajo el nivel del mar y el cangrejo a 3/8 sobre el nivel del mar, es decir, 27/40 negativo y 3/8 positivo, se te pregunta: ¿cuál es la distancia que hay entre la tortuga y el cangrejo?
Para calcular la distancia se tiene que resolver una sustracción: 3/8 menos 27/40 negativos.
Primero se convierten las fracciones en fracciones equivalentes con igual denominador, en este caso 3/8 lo conviertes a 15/40. 7. Posteriormente, aplicando la regla de la sustracción, se convierte la resta en una suma, cambiando al sustraendo por su inverso aditivo, que en este caso es 27/40 positivo, resultando la suma 15/40 más 27/40, al resolver se tiene 42/40, que en el contexto del problema es igual a 1 metro y 2/40, o 1 metro 1/20 que representa la distancia entre la tortuga y el cangrejo.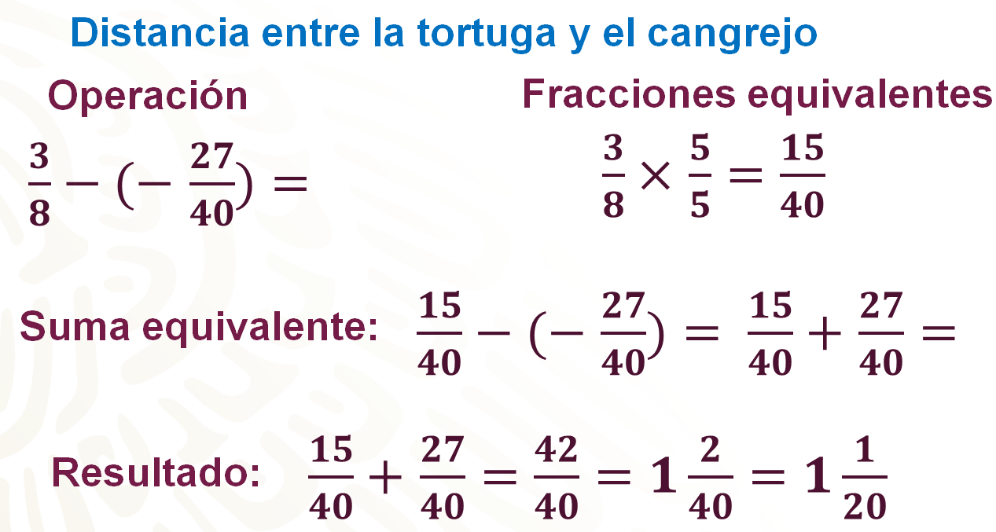
Ya resolviste adiciones y sustracciones de fracciones positivas y negativas, ahora observa un ejemplo en el que se suman números decimales, positivos y negativos. Se te invita a ver el siguiente video y a tomar nota de la información que consideres más relevante. - ¿Cómo sumar y restar números fraccionarios y decimales con signo?
https://www.youtube.com/watch?v=ishwQ7v9W6o
Revisa del tiempo 03:39 al 05:37.
Ahora pondrás en práctica lo que revisaste en el video.
Karla abrió una microempresa con la idea de iniciar un negocio propio. En la siguiente tabla se muestran los saldos diarios obtenidos por Karla durante su primera semana de trabajo.

Se te pregunta: ¿qué significa que el resultado en los días martes, jueves y viernes sea negativo?
¿Cuál es el saldo de la empresa al final de la semana?
En el problema de Karla, las ganancias se representan con números positivos y las pérdidas con números negativos; por lo tanto, en ese caso, los días martes, jueves y viernes hubo pérdidas.
Ahora, para saber el saldo de la empresa al final de la semana, se va a sumar las ganancias y las pérdidas diarias. Para facilitar el procedimiento, primero se sumará por separado las cantidades positivas y negativas.
Recuerda que las cantidades decimales se alinean con el punto decimal y también se coloca el punto en el resultado.
Al resolver las operaciones se observa que Karla tuvo pérdidas de 5 845.70 pesos y ganancias por 3 561 pesos.

Antes de realizar la suma de estos valores, ¿puedes anticipar si en la semana hubo pérdidas o ganancias?
El mayor valor absoluto lo tiene menos 5 845.70, por lo que se deduce que en esa semana en la microempresa de Karla hubo pérdidas.
Pero ¿ya sabes cuál es el saldo de la empresa al final de la semana?
Hay que resolver la operación para averiguarlo.
La adición que permite calcular el saldo de la empresa es 5 845.70 negativo más 3 561.05; para resolverla se calcula la diferencia entre los valores absolutos de las cantidades correspondientes, cuyo resultado es 2 284.65; y como se había anticipado, el resultado es un número negativo, es decir, la microempresa en la primera semana tiene una pérdida de 2 284.65 pesos.

Ya se ha resuelto un problema que involucra sumas de números decimales, positivos y negativos.
Hay que continuar con el problema del negocio de Karla.
De acuerdo con una proyección, Karla espera que la segunda semana la empresa obtenga ganancias totales por 3 150 pesos.
Se te pregunta: ¿cuál debe ser la ganancia de la segunda semana para que, al sumar con el saldo de la primera semana, se cumpla la proyección?
Para saberlo se tiene que calcular la diferencia entre el saldo de la semana 1 y la proyección de la semana 2.
La operación que te lleva a obtener la respuesta es: 3 150 menos 2 284.65 negativo, y como has visto, como restar es equivalente a sumar el inverso aditivo del sustraendo, la adición equivalente es 3 150 más 2 284.65, cuyo resultado es 5 434.65.
Lo anterior indica que, para obtener un saldo total en las dos semanas de 3 150 pesos, las ganancias en la segunda semana tienen que ser de 5 434.65 pesos.

Anota tu respuesta y, si tienes oportunidad, compártelo con tu maestra o maestro a distancia.
Observa una situación problema más.
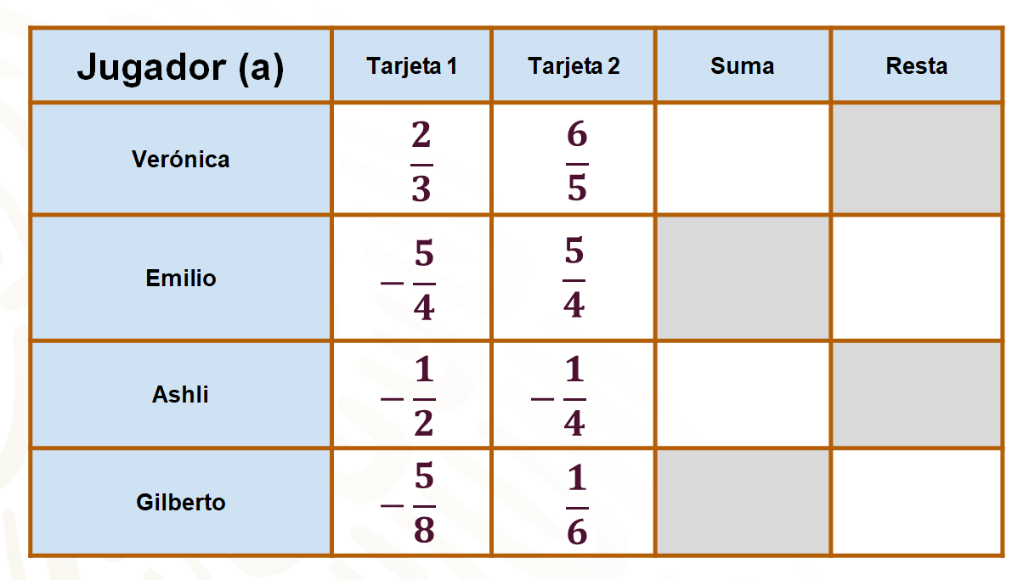
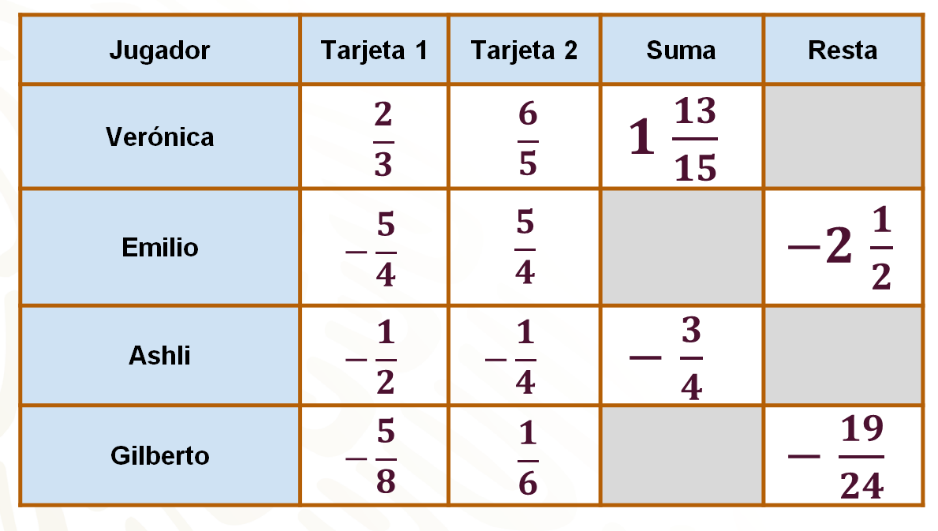
Cuatro amigos decidieron competir para ganarse un premio. El juego consiste en que cada participante tome dos tarjetas al azar. Las tarjetas contienen fracciones: el primero y el tercero que sacan las tarjetas las suman y el segundo y el cuatro, a la fracción de la primera tarjeta, le restan la segunda. El ganador del juego es el que obtiene la fracción mayor.
Observa las tarjetas que sacó cada amigo.
¿Ya estás lista(o) para resolver las operaciones?
Recuerda que Verónica y Ashli tienen que sumar y Emilio y Gilberto tienen que restar a la fracción de la primera tarjeta, la fracción de la segunda.
Resuelve las operaciones para saber quién ganó.
Verónica tiene que resolver la suma 2 tercios más 6 quintos, como ambos son números positivos siguió el procedimiento convencional, convirtió 2 tercios a 10 quinceavos y 6 quintos a 18 quinceavos y realizó la suma, en la que obtuvo 28 quinceavos que simplificado es igual a un entero 13 quinceavos.
Emilio fue el segundo en sacar sus tarjetas, por lo tanto, tiene que resolver una resta. Observa que las fracciones 5 cuartos negativo y 5 cuartos positivo son números opuestos, es decir, que están a la misma distancia del cero; sin embargo, le toca restar sus fracciones lo que significa que sumará el opuesto de 5 cuartos, es decir, 5 cuartos negativo.
Lo siguiente por hacer es sumar los numeradores de donde se obtienen 10 cuartos negativo, que simplificado queda como dos enteros y un medio negativo.
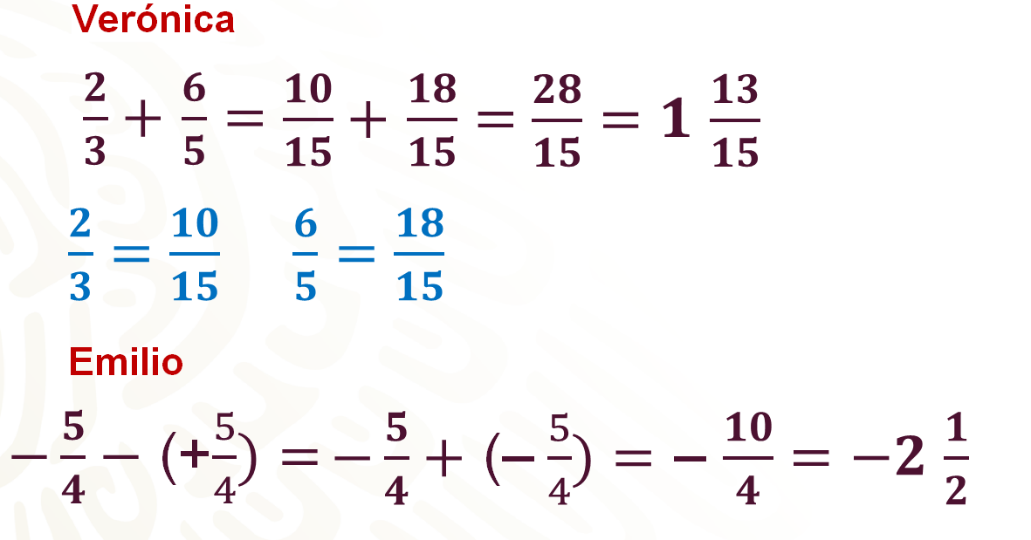
En tercer lugar, Ashli sacó un medio negativo y un cuarto negativo, y le toca sumar sus fracciones: convirtió ½ negativo en 2/4 negativo, y como ambas fracciones son negativas sumó sus valores absolutos y el resultado es una fracción negativa, en este caso es ¾ negativo.
En el último turno, Gilberto sacó a 5 octavos negativo y en el otro 1 sexto positivo, a él le toca restar sus fracciones. Entonces convierte ambas fracciones a veinticuatroavos y suma 15/24 negativo, más el opuesto de 4 veinticuatroavos, que es 4/24 negativo; al resolver la suma se obtienen 19 veinticuatroavos negativos.

Ya que se tienen los resultados de los cuatro amigos, te pregunto: ¿quién ganó el premio?
Observa nuevamente la siguiente tabla ya con los resultados de los cuatro amigos; en este caso, la ganadora es Verónica, no es necesario hacer ninguna comparación, ya que es el único resultado positivo; por lo tanto, es el número mayor, aunque 2 ½ negativo tiene mayor valor absoluto, es el resultado menor.
En casa ¿cómo te fue?, ¿tomaste nota?
Puedes generar en casa más tarjetas, para ver su logras el puntaje de Verónica, quién ganó también en esta ronda.
Ahora, hay que seguir aplicando tus conocimientos con la siguiente situación.
Un buzo trabaja en una plataforma petrolera haciendo reparaciones a las estructuras sumergidas. Inicia su recorrido a nivel del mar. Baja 18 de m para llegar a su equipo de trabajo. Desciende 5 de m para revisar un soporte. Sube 10 de m para reparar una tubería.

Como ya has visto, los descensos bajo el nivel del mar se consideran con números negativos, y los ascensos con números positivos.
Entonces, para conocer la distancia del nivel en la que se encuentra el buzo, se deben sumar números positivos y negativos.
El buzo bajó 18 3/4 de m y luego descendió 5 ½ m, ambas fracciones se representan con números negativos y después se escribe 10 enteros un cuarto positivo. Primero se sumarán los números negativos y, posteriormente, el número positivo.
Para resolver la suma de números negativos, primero se sumará la parte entera, es decir, 18 negativo más 5 negativo que da 23 negativo. Ahora se va a sumar las fracciones, siguiendo los procedimientos conocidos. ½ negativo es equivalente a 2/4 negativo, y al sumar ¾ negativo más 2/4 negativo el resultado es 5/4 negativo y simplificar queda 1 ¼ negativo. Ahora, se suma los resultados, 23 negativo más 1 negativo más ¼ negativo es igual a 24 y ¼ negativo.

Pero después el buzo ascendió 10 ¼ de m, por lo que se sumará este número al resultado anterior, sabiendo que el resultado será un número negativo, ya que 24 ¼ negativo tiene mayor valor absoluto que 10 ¼.
Para resolver la suma, calcula la diferencia entre los valores absolutos de ambos números. Se empieza por la parte entera, 24 menos 10 es igual a 14 y ahora las fracciones 1/4 menos ¼ es igual a cero. Y se sabe que el resultado es un número negativo, es decir, 14 negativo.
Por lo tanto, el buzo se encuentra 14 m bajo el nivel del mar.

A continuación, resuelve un nuevo problema relacionado con el mismo buzo.
Al día siguiente el buzo, desde el nivel del mar, baja 19 m para soldar una pieza; después, sube 4 4/5 de m para instalar un sensor térmico y, finalmente, desciende 8 ¼ de m para fijar una polea.

Revisa el planteamiento del problema. Una vez establecidos los ascensos y descensos, queda la suma: 19 negativo más 4 enteros cuatro quintos, más 8 enteros un cuarto negativo.
Resuelve las operaciones para conocer la posición del buzo.
Separa la parte entera y efectúa las operaciones indicadas aplicando la regla de la adición de números positivos y negativos. 19 negativo más 4 es igual a 15 negativo y 15 negativo más 8 negativo, es igual a 23 negativo, reserva este resultado.
Ahora se suma la parte fraccionaria. Recuerda, primero se convierten a fracciones con igual denominador, en este caso veinteavos, y se calcula la diferencia entre los valores absolutos que en este caso es 11/20, que es positivo porque 16/20 tiene mayor valor absoluto.
Como te darás cuenta, el buzo se encuentra trabajando a 22 9/20 de m bajo el nivel del mar.

Para poner en práctica lo que has aprendido, en esta sesión se te propone la siguiente actividad. Seguramente ya has resuelto un cuadrado mágico.
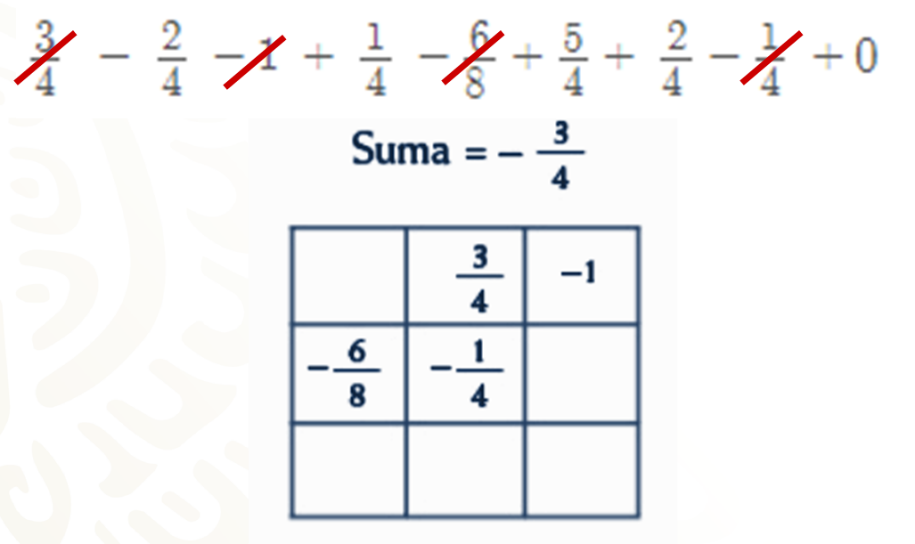
En un cuadrado mágico, Ia suma de números en línea vertical, horizontal o diagonal siempre dan el mismo resultado.
Hay que resolver uno.
En el cuadrado mágico el resultado de cada suma debe ser igual a 9 negativo.
Una estrategia útil cuando conoces el valor de las casillas de la línea es restar al resultado que se necesita, en este caso 9 negativo, la suma de los valores conocidos.

Por ejemplo, para la segunda fila se resuelve 9 negativo menos 3 negativo, menos 1 negativo.
Aplicando el inverso aditivo de los números que se restan, se obtiene la suma 9 negativo más 3 positivo más 1 positivo, que da como resultado 5 negativo.
Para completar la última columna, se sigue un procedimiento similar al anterior: 9 negativo, menos 2 negativo, menos 1 negativo.
Aplicando el inverso aditivo, se obtiene la suma 9 negativo más 2 positivo más 1 positivo, que da como resultado 6 negativo.
¿Ya tienes los números que faltan? Trata de calcularlos mentalmente.
El cuadrado mágico queda completo, como se muestra, a continuación. Realiza las operaciones necesarias para comprobar que la suma 9 negativo se cumple en todos los casos.

Después de verificar los resultados. Es momento de recuperar algunos aprendizajes vistos en esta sesión, los cuales son:
- El valor absoluto de un número representa la distancia desde ese número al cero.
- Los números opuestos o simétricos son aquellos que se encuentran a la misma distancia del cero, en lados opuestos.
- Para sumar números positivos y negativos, cuando tienen el mismo signo, se suman los valores absolutos y el resultado tiene el signo de ambos números.
- Cuando se suma un número positivo y uno negativo, se calcula la diferencia entre los valores absolutos y el resultado será del tipo de número que tiene mayor valor absoluto.
- Para restar números positivos con negativos, se suma al minuendo, el opuesto o inverso aditivo del sustraendo.
Como te puedes dar cuenta, las mismas reglas que se usan con los números enteros se aplican a las fracciones y decimales.
Recuerda, que, para conocer más de este tema, puedes consultar otras fuentes, también puedes consultar tu libro de texto de Matemáticas 1 y resolver los ejercicios propuestos para seguir practicando al respecto del tema. Anota tus dudas o comentarios y si tienes oportunidad compártelos con tu maestro o maestra a distancia.
El reto del hoy:
Completa el cuadrado mágico que se muestra a continuación. Toma nota de los valores que se muestran.
En este caso, la suma de todas las líneas tiene que ser ¾ negativo. Como verás ya se muestran números que completan el cuadrado y algunos ya están colocados dentro del mismo.
Recuerda que para resolverlo debes realizar, igual que en el anterior, la diferencia entre la suma que es ¾ negativo y los números que conoces; por ejemplo, ¾ negativo menos ¾ positivo, menos ¼ negativo.
Aplicando el inverso aditivo realizas la suma ¾ negativo más ¾ negativo más ¼ positivo, que da 5/4 negativo.
Completa las casillas que faltan. Comparte tu trabajo con tu profesor o profesora a la distancia y si tienes dudas compártelas para aclararlas.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas