Polígonos y su contorno
Polígonos y su contorno
Aprendizaje esperado: calcula el perímetro de polígonos y del círculo, y áreas de triángulos y cuadriláteros, desarrollando y aplicando fórmulas.
Énfasis: analizar las fórmulas del perímetro de polígonos regulares e irregulares
¿Qué vamos a aprender?
Hoy trabajarás un tema de geometría, relacionado con el contorno de las figuras; así es: el perímetro. Asimismo, observarás las diferencias y las relaciones entre las fórmulas, en polígonos regulares e irregulares, así como la construcción de estas mismas.
¿Qué hacemos?
Como sabes, hacer ejercicio es un hábito saludable, te ayuda a reducir el estrés, a prevenir problemas de salud y, por supuesto, te ayuda a sentirte mejor. Hay personas, por ejemplo, que solían salir los fines de semana, por las mañanas, a correr a un deportivo cercano a su domicilio; por las circunstancias actuales ya no es posible hacerlo, pero es agradable para ellas correr en la pista que está alrededor de todo el terreno. Una de estas personas decidió investigar con el responsable del lugar en el cual ella solía correr, cuantos metros recorre en una vuelta completa alrededor del deportivo, para ello el responsable le enseño un plano.
Observa la siguiente imagen del plano, se sugiere que lo repliques en tu cuaderno.
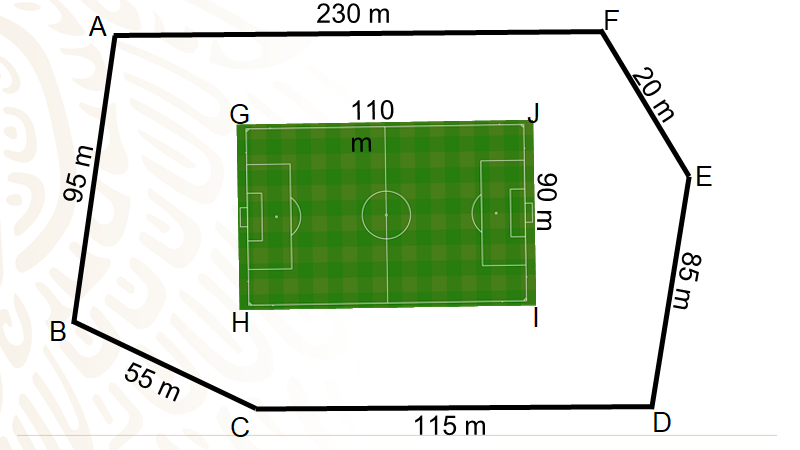
En la imagen puedes observar el deportivo delimitado por el contorno de color negro; y además puedes notar que al centro hay una cancha que es utilizada, principalmente, para jugar futbol rápido.
La medida de cada lado del deportivo es diferente, el segmento AB mide 95 metros, el segmento BC 55 metros, el segmento CD 115 metros, el segmento DE 85 metros, el segmento EF mide 20 metros y el último segmento FA mide 230 metros.
Para empezar, observa bien la figura que tiene el deportivo, responde la siguiente pregunta: ¿qué forma tiene el deportivo?
La respuesta es que el deportivo tiene una forma de polígono irregular.
Ahora piensa que el terreno es totalmente plano, y que la persona corre siguiendo en la medida de lo posible el perímetro del terreno; con estos datos, responde la siguiente pregunta:
Aproximadamente, ¿qué distancia recorrerá, la persona, al dar una vuelta completa al deportivo?
Como se mencionó el deportivo tiene forma de un polígono irregular, ya que como sabes en este tipo de figuras no todos sus lados tienen la misma longitud y no todos sus ángulos interiores miden lo mismo.
Ya que conoces qué forma tiene el deportivo, puedes dar respuesta a la segunda pregunta que se planteó, la cual fue: ¿Qué distancia recorrerá la persona al dar una vuelta completa?
¿Qué operación realizarías para determinar esta distancia?
La respuesta es una adición, en la cual calcularás el perímetro del deportivo efectuando la suma de todos sus lados.
En ese sentido el segmento AB mide 95 metros + el segmento BC que mide 55 metros + 115 metros que mide el segmento CD + el segmento DE que mide 85 metros + EF con medida de 20 metros + FA que mide 230 metros, te dará como resultado 600 metros.
| AB | 95 | |
| BC | 55 | |
| CD | 115 | |
| DE | 85 | |
| EF | 20 | |
| FA | 230 | |
| 600 |
Como pudiste darte cuenta, se calculó el perímetro de la figura y éste se interpreta como la distancia aproximada que corrió la persona; con una vuelta completa al deportivo, en total fueron 600 metros.
Ahora bien, si esa persona decidiera correr alrededor del campo de fútbol, ¿cuántas vueltas debería darle para conseguir los 600 metros que recorrió en una vuelta completa alrededor del deportivo?, para que te des una idea, observa la siguiente imagen.
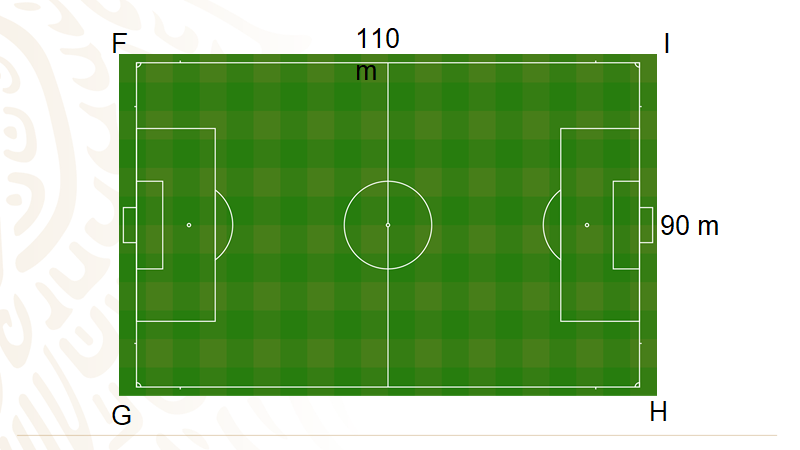
Como puedes ver, el campo de futbol tiene forma rectangular, mide 110 metros de largo y 90 metros de ancho, las principales características del rectángulo son que tiene lados paralelos iguales dos a dos, y sus cuatro ángulos son rectos; de acuerdo con estas características se puede decir que, el rectángulo es un paralelogramo y forma parte de la familia de los cuadriláteros.
Para contestar a la pregunta: ¿cuántas vueltas debería darle la persona para conseguir los 600 metros que recorre en una vuelta completa alrededor del deportivo?
Debes encontrar primero el perímetro de la cancha. ¿Cómo puedes obtenerlo?, ¿Cuál es el resultado?
El perímetro de la cancha es de 400 metros. Para sacar este valor lo que se hizo fue: sumar el valor de los cuatro lados de la cancha, es decir, 110 metros + 90 metros + 110 metros + 90 metros; lo cual da como resultado: 400 metros.
Entonces, ¿cuántos metros más faltan para 600 metros?
Para conocer este dato, debes restar 600 metros -400 metros, esto da como resultado 200 metros. Si por una vuelta completa alrededor del campo fueron 400 metros, para completar los 600 metros se debe dar media vuelta más. Por lo que una vuelta completa alrededor del deportivo equivale a dar una vuelta y media alrededor del campo de fútbol.
Es interesante saber que la persona puede correr lo mismo dando una vuelta y media al campo de fútbol, que si le diera una vuelta completa al deportivo.
Alguna vez te has preguntado: ¿cómo encontraban el perímetro de las figuras en la antigüedad?
Porque hoy en día se conocen varios instrumentos que ayudan a medir cualquier objeto, y que antes no existían, tales como las cintas métricas o los flexómetros, los distanciómetros sónicos, los topómetros, entre otros más.
¿Qué te parece si revisas el siguiente audiovisual que te ayudará a resolver esta duda?
- “Obtención del perímetro en la antigüedad”
https://youtu.be/CpkAppRUgoU
Como observaste, es interesante la manera en que se medía la longitud en la antigüedad, ya que las civilizaciones tuvieron la necesidad de medir cosas, y para ello requerían de utilizar las medidas del cuerpo, como la longitud del pie, el codo, la longitud entre el dedo meñique hasta el dedo pulgar, que se conoce como la cuarta, entre otras; y es sorprendente que hoy en día siguen siendo útiles.
Esta última forma de medir, quizás te recuerde cuando de pequeño jugabas con tus amigos a las canicas, en donde golpeabas la canica adversa, y la distancia entre éstas debería ser menor a una cuarta para poder ganar.
Volviendo al tema de los contornos en polígonos regulares, ¿has observado imágenes con la forma que tienen las celdas de un panal de abejas?
En él puedes notar que la construcción de la colmena está realizada con polígonos, específicamente con hexágonos regulares y es un buen ejemplo que puedes observar en la naturaleza. Un panal: es una estructura formada por celdillas de cera que comparten paredes en común, y las abejas lo utilizan para contener a sus larvas, para poder ilustrarlo, observa la siguiente imagen.
En la imagen, puedes ver cómo las abejas están construyendo sus celdillas; las cuales terminan tomando forma de un polígono regular, llamado hexágono. Se sugiere escribir la siguiente pregunta para reflexionar:
¿Cuál será la medida de cada lado de la celdilla?
El tamaño de la celdilla es un factor muy importante, incluso se puede decir que, sin el tamaño adecuado, las abejas no pueden vivir en armonía con la naturaleza. Varios investigadores han realizado estudios para determinar la medida de un lado de la celdilla, siendo ésta aproximadamente de 5.44 milímetros.
Con el dato anterior puedes encontrar el perímetro aproximado de una celdilla; para ello se sugiere que dibujes en tu cuaderno o en alguna hoja reutilizable, la siguiente imagen.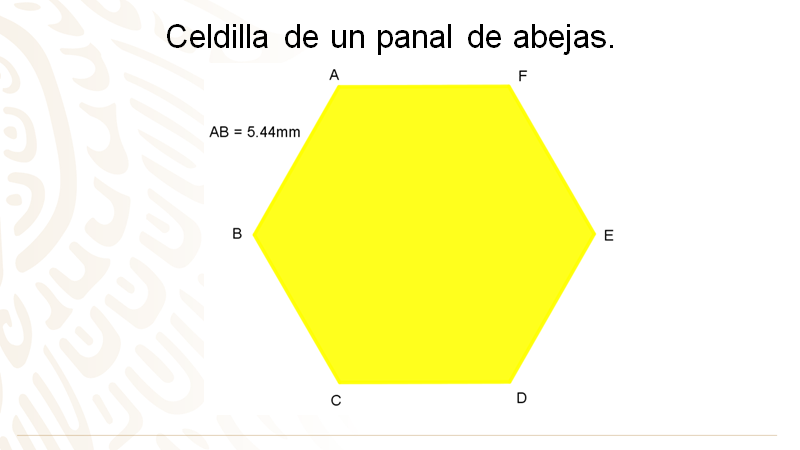
En la imagen puedes observar la celdilla de un panal de abejas en color amarillo. La medida de cada lado de la celdilla es de aproximadamente 5.44 milímetros.
Bien, calcula el perímetro aproximado de la celdilla, el cual puedes obtenerlo realizando una adición, ¡o una multiplicación!, ya que sus lados son iguales por ser un polígono regular. Debes tener en mente que todos los polígonos regulares tienen sus lados iguales y sus ángulos interiores también valen lo mismo, por esto, para obtener el perímetro de manera más sencilla y rápida, puedes ocupar el producto.
Multiplicarás el número de lados, que en este caso son 6, por el valor de la medida de uno de ellos, que es 5.44 milímetros; por lo que se puede decir que aproximadamente el contorno, o perímetro de una celdilla del panal de abejas, es de 32.64 milímetros.
Analizando el ejemplo anterior, se determina que la fórmula para encontrar el perímetro de cualquier polígono regular, será igual al valor de uno de sus lados por la cantidad de lados que tiene la figura. Por ejemplo, para el triángulo equilátero su fórmula es P = tres veces la medida de su lado (3 x L), para el cuadrado el P = cuatro veces su lado (4 x L), del pentágono es P = cinco veces su lado (5 x L), y así sucesivamente.
Observa el siguiente recurso visual, con polígonos donde su lado es de medida 10. - Perímetro de polígonos regulares de 3 a 8 lados.
Otro ejemplo relacionado con perímetros es el siguiente:
La tía Lili, que vive en el estado de Pachuca, tiene una pequeña granja que quiere cercar para que pasten sus vacas. ¿Cuántos metros de malla de alambre se requieren para cercar el terreno de la tía Lili?
Para este ejemplo se sugiere que dibujes en tu cuaderno el siguiente plano del terreno de la tía Lili.

En la imagen puedes observar el terreno, en color verde. Las medidas de cada lado son diferentes, el segmento AB mide 195 metros, el segmento BC 134 metros, 210 metros el segmento CD, 98 metros el segmento DE, el segmento EF mide 310 metros, y el último segmento FA tiene como valor 464 metros.
Como verás el terreno de la tía Lili no tiene sus lados iguales, como en el caso del panal, pero sí tiene sus lados como el deportivo del primer ejemplo; ya sabes que a este tipo de figuras se les conoce como polígono irregular, puedes ver que sus lados no son iguales y tampoco sus ángulos internos miden lo mismo; pero, ¿cómo encontrarás el perímetro de este polígono irregular?
La ventaja, es que ahora sabes que tienes que sumar todos los lados de la figura, y así encontrarás los metros de malla de alambre que necesita comprar la tía Lili para cercar su terreno.
Así, el perímetro del terreno de la tía Lili, se sacará sumando el valor del segmento AB que mide 195 metros, más el valor del segmento BC, 134 metros; más 210 metros, que es el valor del segmento CD; más el segmento DE que es 98 metros, más 310 metros del segmento EF, más el último segmento FA que es 464 metros; teniendo como resultado, 1 411 metros. Por lo que la tía necesita comprar, 1 411 metros de reja de alambre para cercar su terreno.
Como ves, es útil conocer la medida del contorno de superficies para que como en este último ejemplo se evite gastar de más y llevar el suficiente material para poder cercar todo el terreno.
Conocer el perímetro te puede ser de gran utilidad en muchos otros casos; por ejemplo, ¿tú sabes lo que es el zoclo o también conocido como rodapié?
Si no sabes, el zoclo es la moldura de madera o cerámica que se coloca en la base de la pared, entre el piso y el muro, para que se protejan de golpes. Ahora fíjate en la siguiente figura que es del croquis de una sala en la que se pondrá este zoclo o rodapié.
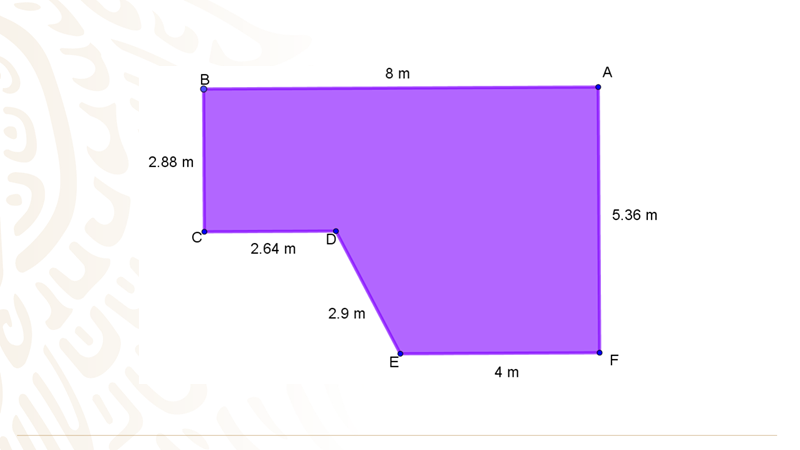
Como puedes observar, la figura es la de un polígono irregular; por lo que habrá que sumar uno por uno todos sus lados.
Dibuja la figura y observa que la distancia del segmento AB es de 8 metros, de BC es 2.88 metros, de CD mide 2.64 metros, el segmento DE es de 2.9 metros, el EF mide 4 metros y el segmento FA mide 5.36 metros.
Después de haber visto las medidas, la pregunta es: ¿cuál será la longitud del rodapié?
Para responder esta pregunta, debes realizar la suma de 8+ 2.88 + 2.64 + 2.9 + 4 + 5.36.
La cual da como resultado 25.78 metros, que corresponde a la longitud total del zoclo o rodapié que se necesitará.
Recapitulando lo que has visto en la sesión del día de hoy:
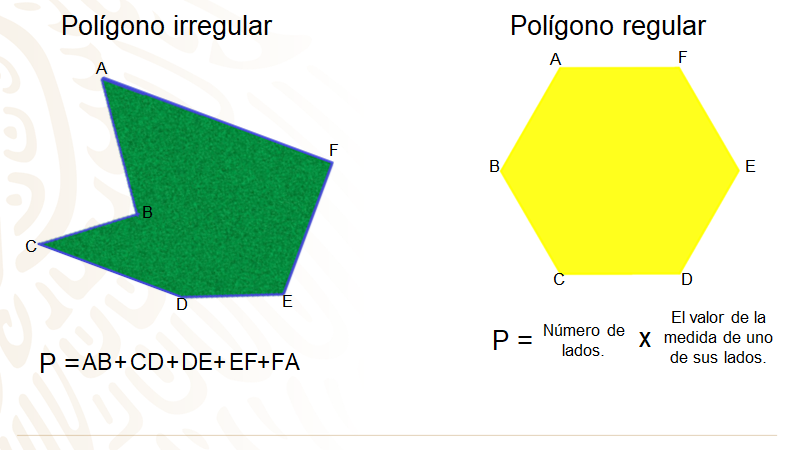
Recuerda que en los polígonos irregulares es necesario sumar todos los lados de la figura, uno por uno. Mientras que en los polígonos regulares se puede multiplicar la medida del lado por la cantidad que éste tenga.
Has terminado el tema del día de hoy.
El reto de hoy:
Apoya tus anotaciones, y el conocimiento adquirido, revisando en tu libro de texto el tema “Perímetro de polígonos” y realiza las actividades que ahí se sugieren.
Recuerda que puedes encontrar los libros de texto en la página: conaliteg.sep.gob.mx/
¡Buen trabajo!
Gracias por tu esfuerzo.