Plantear problemas de números con signo en diversas situaciones
Aprendizaje esperado: resuelve problemas de suma y resta con números enteros, fracciones y decimales positivos y negativos.
Énfasis: Números con signo en diversas situaciones
¿Qué vamos a aprender?
En esta lección reflexionarás acerca del uso de los números con signo aplicados en la resolución de situaciones problemáticas en diversos contextos cotidianos.
¿Qué hacemos?
Antes de comenzar es importante mencionar que al resolver un problema matemático es fácil confundirse si no llevas un orden. Para evitar que esto suceda te compartimos estos sencillos pasos que te permitirán tener una mejor comprensión para la resolución de cualquier problema.
- Leer con detenimiento para analizar el problema y comprender tanto el contenido como la pregunta.
- De este análisis debes extraer y escribir en tu cuaderno los datos que te permitan llegar a una solución satisfactoria.
- Con los datos hacemos un planteamiento numérico. ¡Eso sí!, con claridad y limpieza.
- Ubica las operaciones necesarias y después resuélvelas.
- Una vez resueltas las operaciones, escribe la solución, y no olvides anotar las respectivas unidades.
Observa el siguiente video del minuto 0:23 a 01:02, donde se plantea una actividad y resolvámosla.
- Problemas con números enteros
https://www.youtube.com/watch?v=J5m-jObxw-I&feature=youtu.be
Para resolver este planteamiento usaremos la recta numérica, ubicando los datos que tenemos de la siguiente manera:

Como sabes, para encontrar la distancia entre dos puntos en la recta numérica debemos obtener la diferencia que hay entre estos. Para ello debemos plantear la siguiente operación:

El 8 positivo corresponde a la altura sobre el nivel del mar a la que vuela el ave y el 13 negativo indica la profundidad a la que llegó el ave.
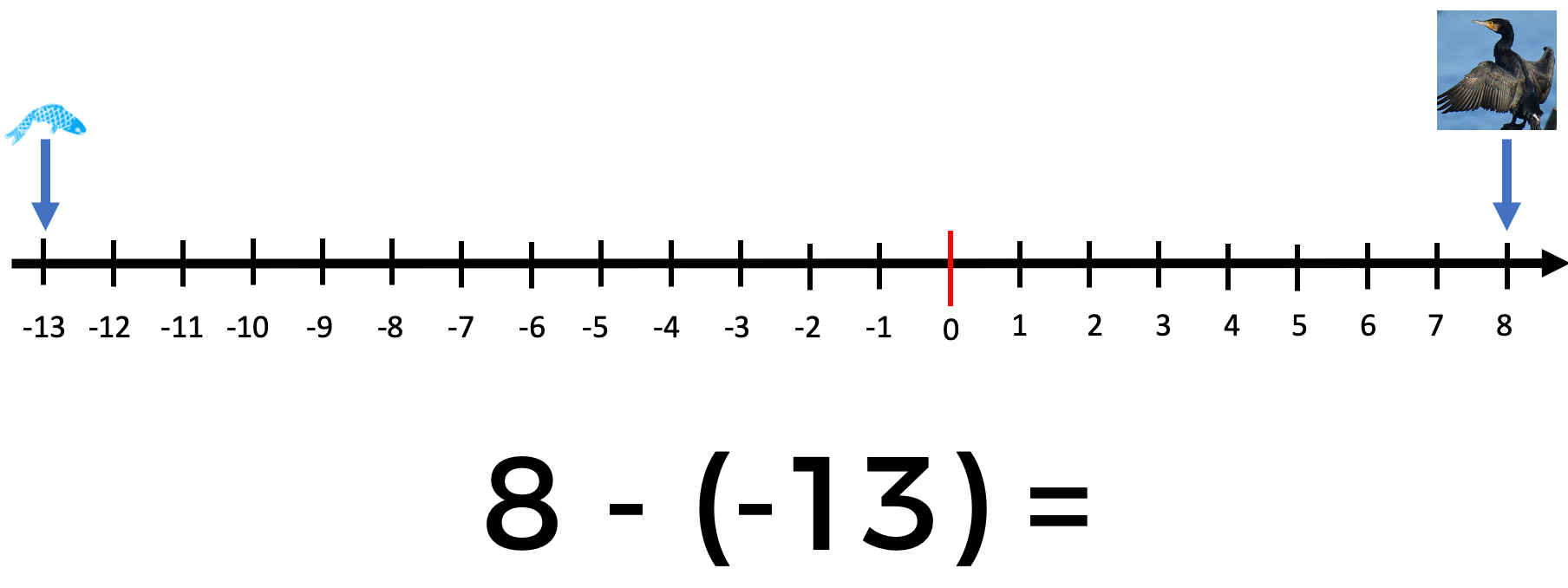
Al obtener la diferencia entre estos dos números estamos realizando una resta de números con signo, por lo tanto, debemos cambiar el sustraendo por su simétrico. Al cambiar el 13 negativo por su simétrico, la sustracción de nuestro problema original cambia a una adición.
En este caso el simétrico de 13 negativo es 13 positivo. y la operación queda como 8 positivo más 13 positivo, y da como resultado 21.
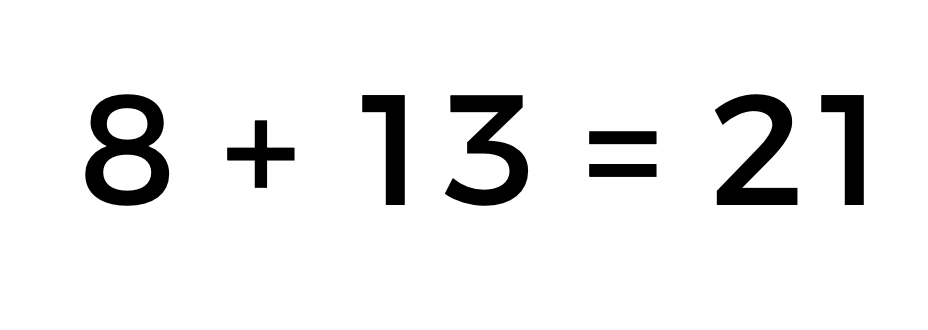
Por lo tanto, la distancia que hay entre la altura del vuelo del ave y la profundidad de su inmersión para pescar es de 21 metros.
Esto se puede comprobar sobre la recta numérica tomando en cuenta la distancia tanto de vuelo como de inmersión, representadas con una unidad de referencia que es el nivel del mar.
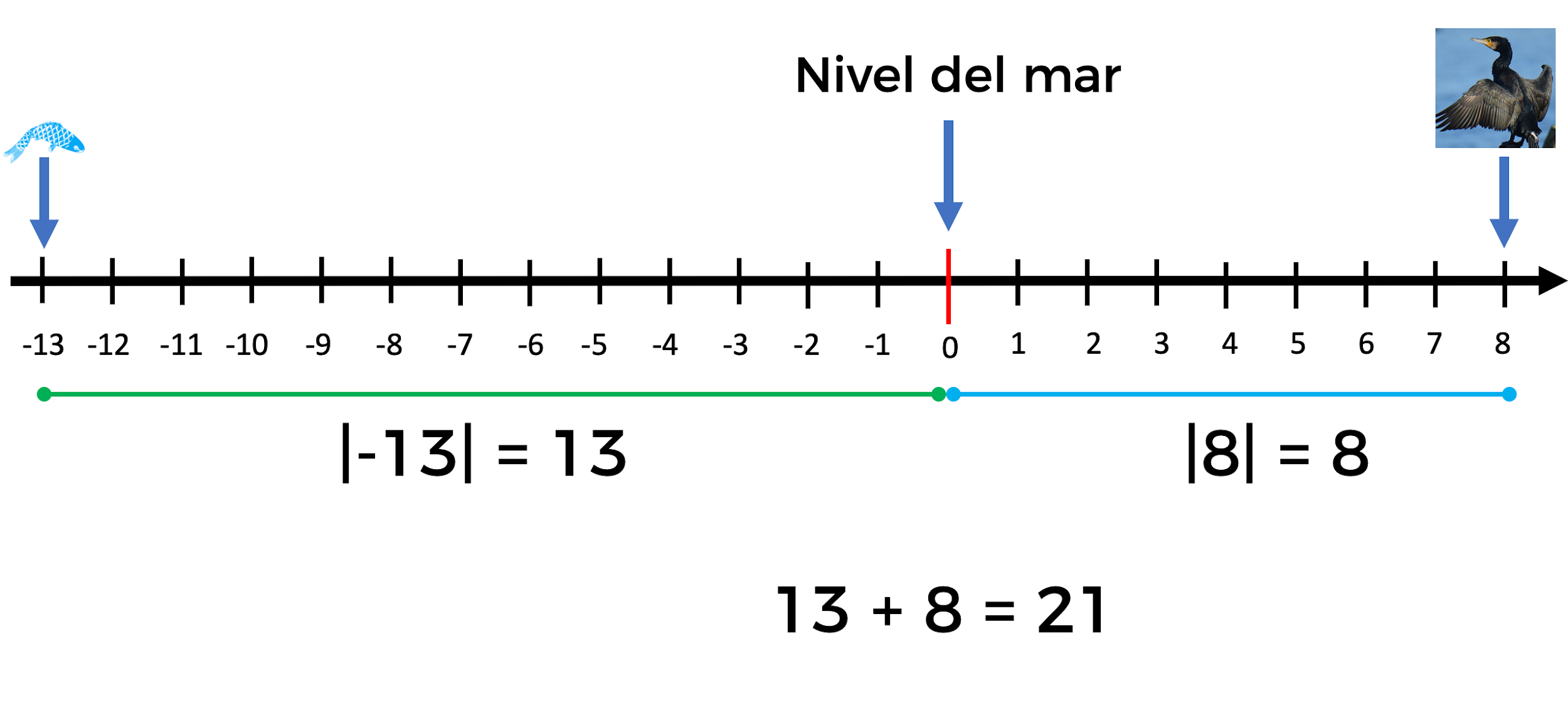
Para seguir practicando las operaciones con números positivos y negativos.
Plantemos otra actividad.
Imagina que un grupo de estudiantes decide crear una caja de ahorro muy peculiar en la cual pueden pedir dinero prestado a la persona que lleva el control del presupuesto, pero con el compromiso de pagar su deuda. Lucía, la alumna que administra, tiene que llevar algún método de registro para tener el control de quienes deben y quienes han pagado. El tener registrada y ordenada dicha información ayuda a que no haya pérdidas.
En esta tabla podemos ver el registro que lleva Lucía, de los alumnos que deben a la caja y lo que han pagado.
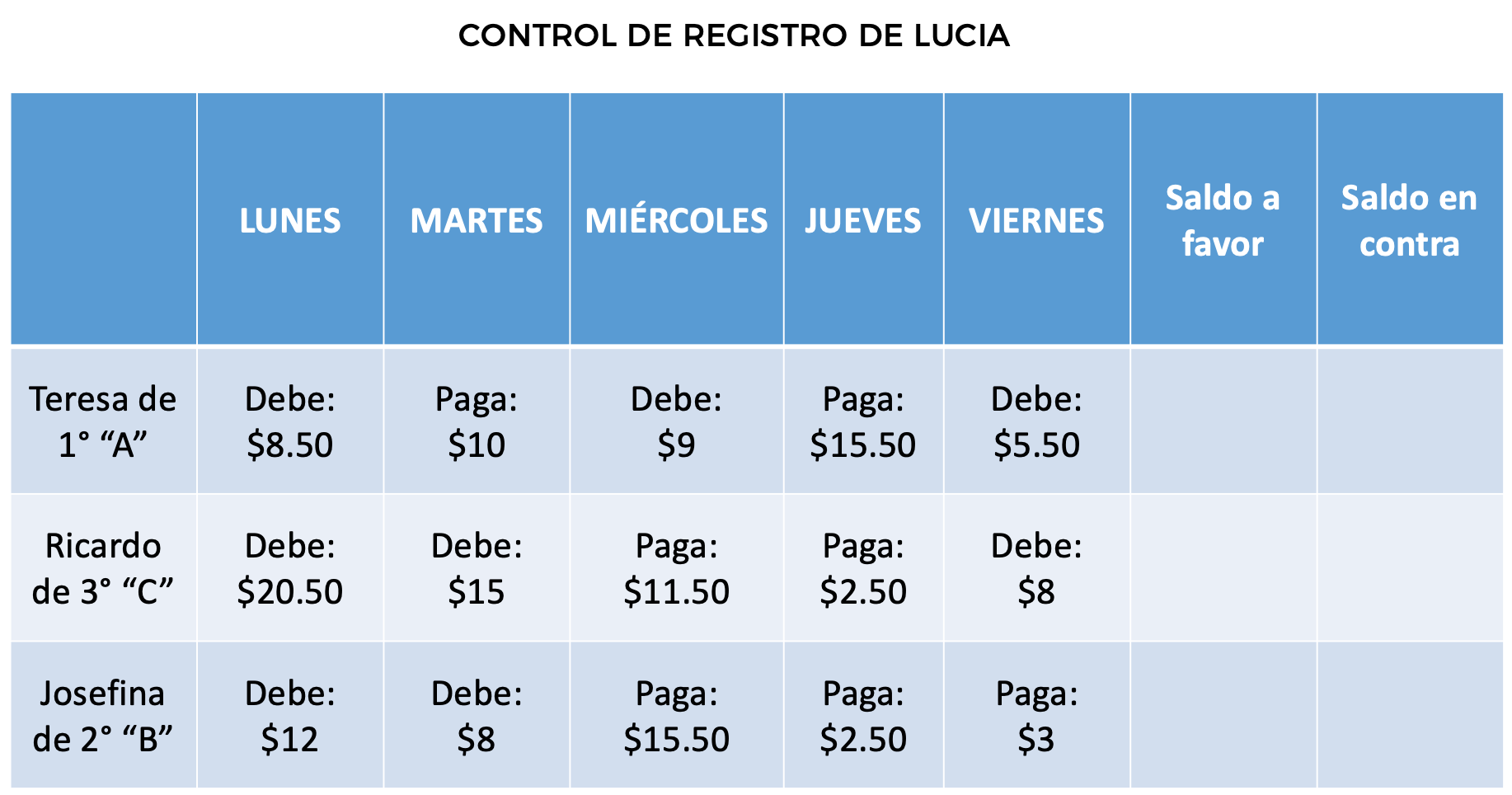
Para saber si Ricardo de 3° “C” tiene un saldo a favor o en contra, planteamos la siguiente operación:
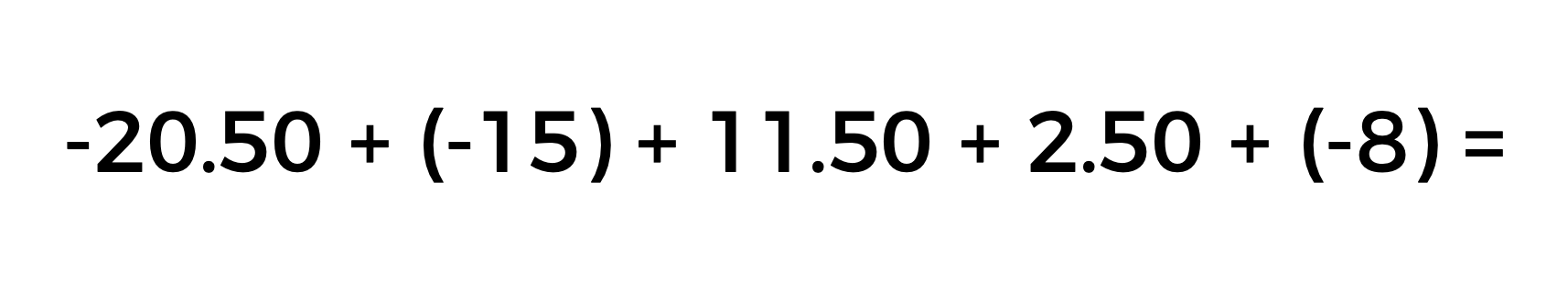
En la operación que se está planteando es importante observar que el dinero que Ricardo debe estar representado con números negativos, mientras que los números positivos corresponden a lo que paga.
Una estrategia que podemos utilizar es sumar por separado los números negativos y positivos:
Primero sumemos los números negativos:

Ahora sumemos los números positivos:

Por último, podemos sumar estos dos resultados parciales para saber si Ricardo tiene un saldo a favor o le debe dinero a Lucía.

El resultado final es -29.50 y si recordamos que estamos hablando de dinero y las unidades son los pesos, entonces Ricardo debe $29.50 pesos.

Recuerda que cuando sumamos números con el mismo signo, se suman los valores absolutos de los números y el resultado conserva el signo de ambos. Y cuando sumas números con diferente signo, al valor absoluto del mayor se le resta el valor absoluto del menor, y el resultado tendrá el signo del número con mayor valor absoluto.
Con este recordatorio, podemos calcular si la alumna Teresa tiene un saldo en contra o a favor. Hagamos el planteamiento del problema:

Siguiendo el procedimiento del planteamiento anterior. Primero sumamos los números negativos.
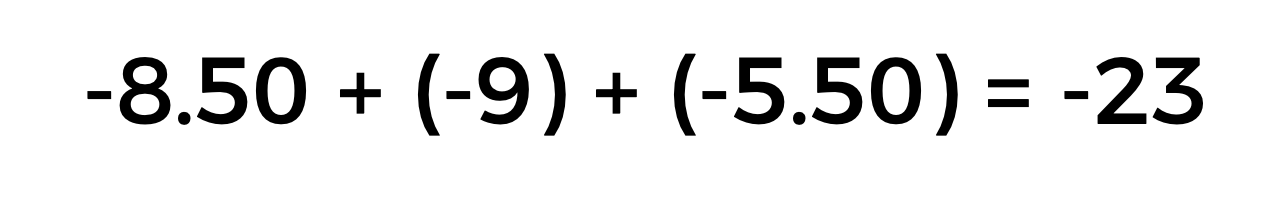
En seguida sumamos los números positivos.

Por último, sumamos los resultados parciales:
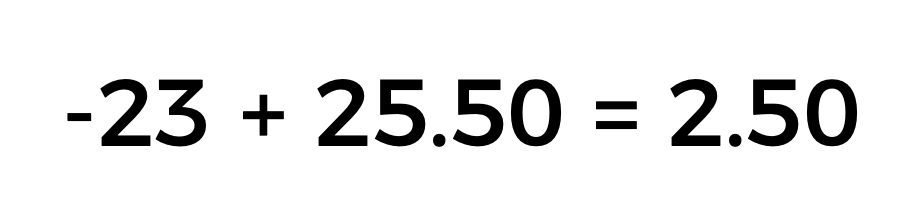
No olvides que este resultado representa una cantidad de dinero y en este caso Teresa tiene un saldo de $2.50 pesos a favor.
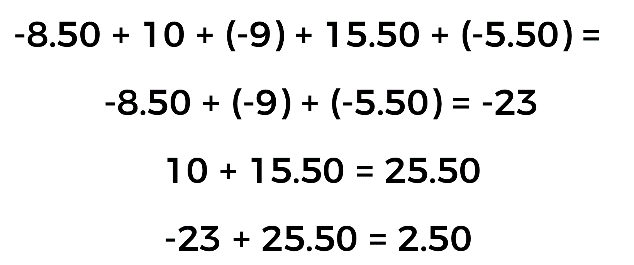
¿En qué otras situaciones se aplican las operaciones de números positivos y negativos?
Resolvamos un problema más sobre una situación que viven las personas que usan automóvil, en su vida diaria:
Durante el primer mes del año, el litro de gasolina subió 5 centavos, el segundo bajó 27 centavos, el tercero bajó 40 centavos y para el cuarto mes bajó 4 pesos con 80 centavos. Si el costo de la gasolina, antes de tener variaciones en su costo era de $21.76 por litro, ¿cuál fue el costo del litro de gasolina durante el cuarto mes del año?
Para responder a esta pregunta, nos apoyaremos en la información de un libro de texto de matemáticas.
Puedes buscar en tu libro de texto el tema para resolver problemas de suma y resta con números enteros, fracciones y decimales positivos y negativos, y comparar las actividades propuestas, así como la información que aparece.
Cuando se tiene una suma de dos números enteros con el mismo signo, se suman los valores absolutos de los números y se conserva el signo en el resultado. Por ejemplo:
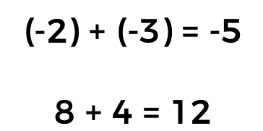
Cuando se tiene una suma de dos números enteros con signo diferente, se restan los valores absolutos de los números y se agrega al resultado el signo del sumando con valor mayor absoluto. Por ejemplo:
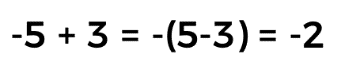
Ya que se conserva el signo del cinco, que es mayor a tres.
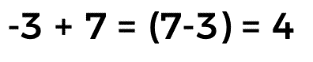
Ya que se conserva el signo del siete, que es mayor a tres.
Resta de números positivos y negativos.
Dos números que tienen el mismo valor absoluto, pero que tienen signos distintos, se llaman simétricos.
Si a y b son números con signo, la resta a – b equivale a la suma a + (-b), donde -b es el simétrico de b.
Para dar respuesta a la pregunta ¿Cuál fue el costo de la gasolina, por litro, durante el cuarto mes del año?, retomaremos lo que acabas de leer.
Podemos representar los datos del problema con una operación.
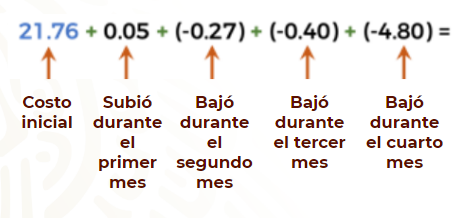
Se trata de una situación donde el costo sube y baja, por lo tanto, debemos utilizar números con signo, es decir, positivos para representar el costo cuando sube y negativos para representar el costo cuando baja.
Debemos aplicar la misma estrategia que en los ejercicios anteriores. Primero sumamos los positivos y luego los negativos, por último, realizamos la suma de los resultados parciales.

De este modo, podemos afirmar que durante el cuarto mes del año la gasolina tuvo un costo de $16.34 por litro.
En tu libro de texto podrás encontrar otros problemas similares a este tipo de situaciones.
Para ayudarte con los problemas que encontrarás en tu libro, realicemos una última actividad que puede resultarte interesante para fortalecer lo que has aprendido durante las sesiones. Se trata de un ¡cuadrado mágico!
Los cuadrados mágicos son divertidos e interesantes. Muchos siglos antes de que los sudokus aparecieran en la Tierra, nacieron los cuadrados mágicos: una cuadrícula llena de números donde cada columna, cada fila y cada diagonal suman lo mismo. El primer cuadrado mágico conocido fue chino.
Te explicaremos brevemente en qué consiste un cuadrado mágico y el porqué es mágico.
Se trata de un cuadrado dividido a su vez en 9 cuadrados iguales.

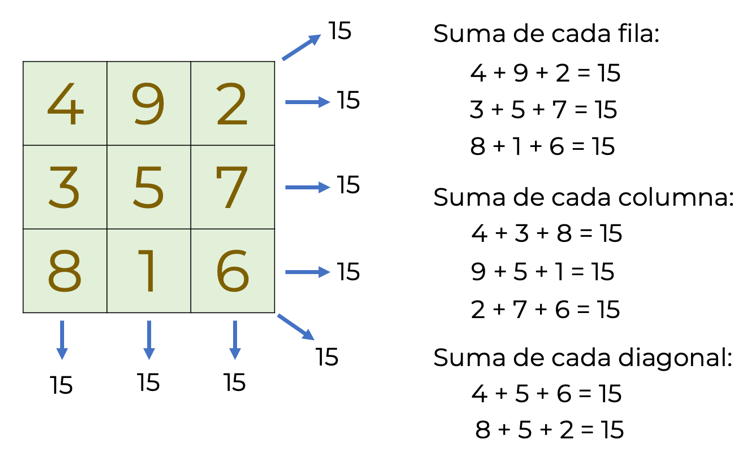
En él debemos colocar números, por ejemplo, del 1 al 9, de tal forma que, al sumar los números de cada columna, fila y diagonal, el resultado sea siempre el mismo, en este caso debe ser 15.
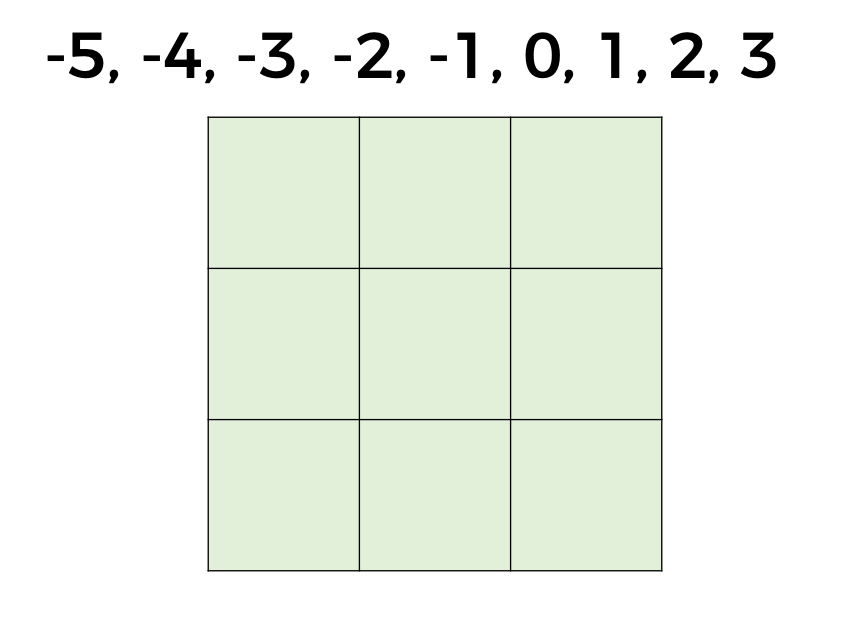
Vamos a resolver el siguiente cuadrado mágico, en el que utilizaremos los números negativos y positivos, ¿qué te parece si utilizamos del 5 negativo al 3 positivo?
Recuerda que al sumar los números de cada una de las filas, columnas y diagonales del cuadrado mágico el resultado debe ser el mismo. En este caso la suma debe ser igual a 3 negativo.
En la siguiente imagen observa que ya hay algunos números escritos en nuestro cuadrado mágico.
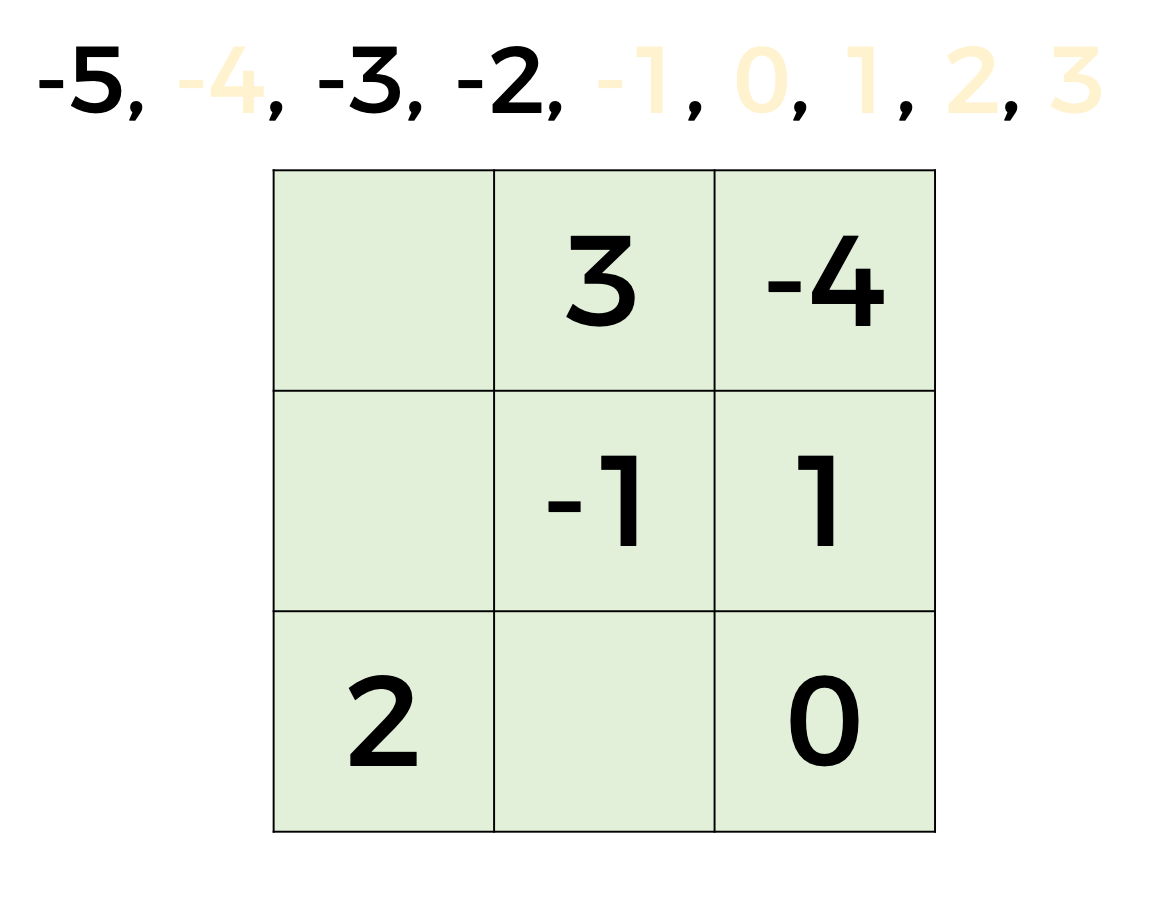
Ahora debes anotar los números que falten. Una estrategia que podemos utilizar para encontrar los números que hacen falta en dicho cuadrado mágico es precisamente aplicando lo que hemos visto durante esta lección.

Si observas con atención, en la fila dos, la suma de uno negativo (-1), más uno positivo (1), más el número que hace falta, debe dar como resultado tres negativos.
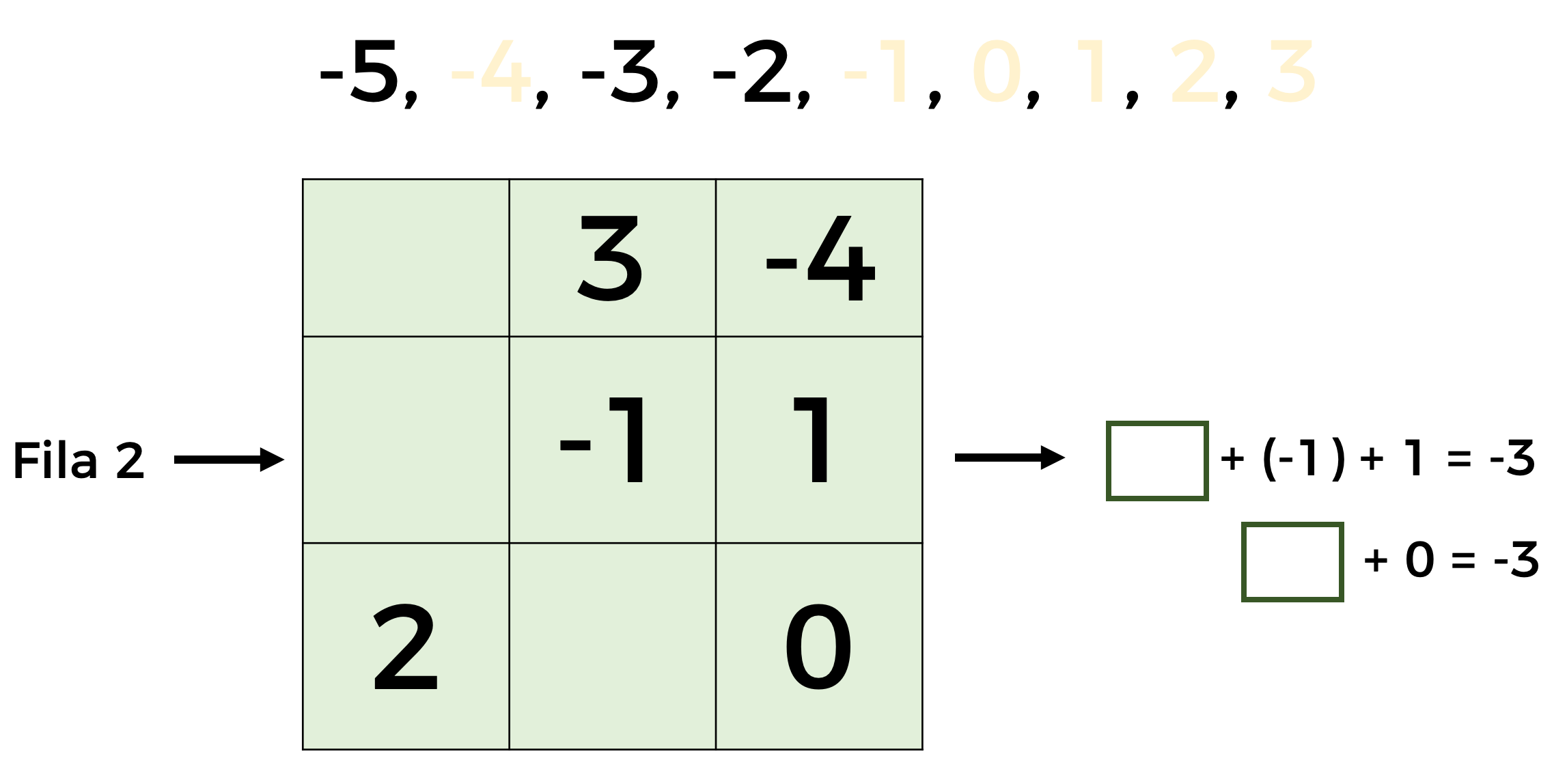
En esa misma operación, poder ver que la suma de uno negativo, con uno positivo, da como resultado 0. Entonces, ¿cuál es el número que debería ir para que se cumpla la condición del cuadrado mágico del renglón en cuestión?
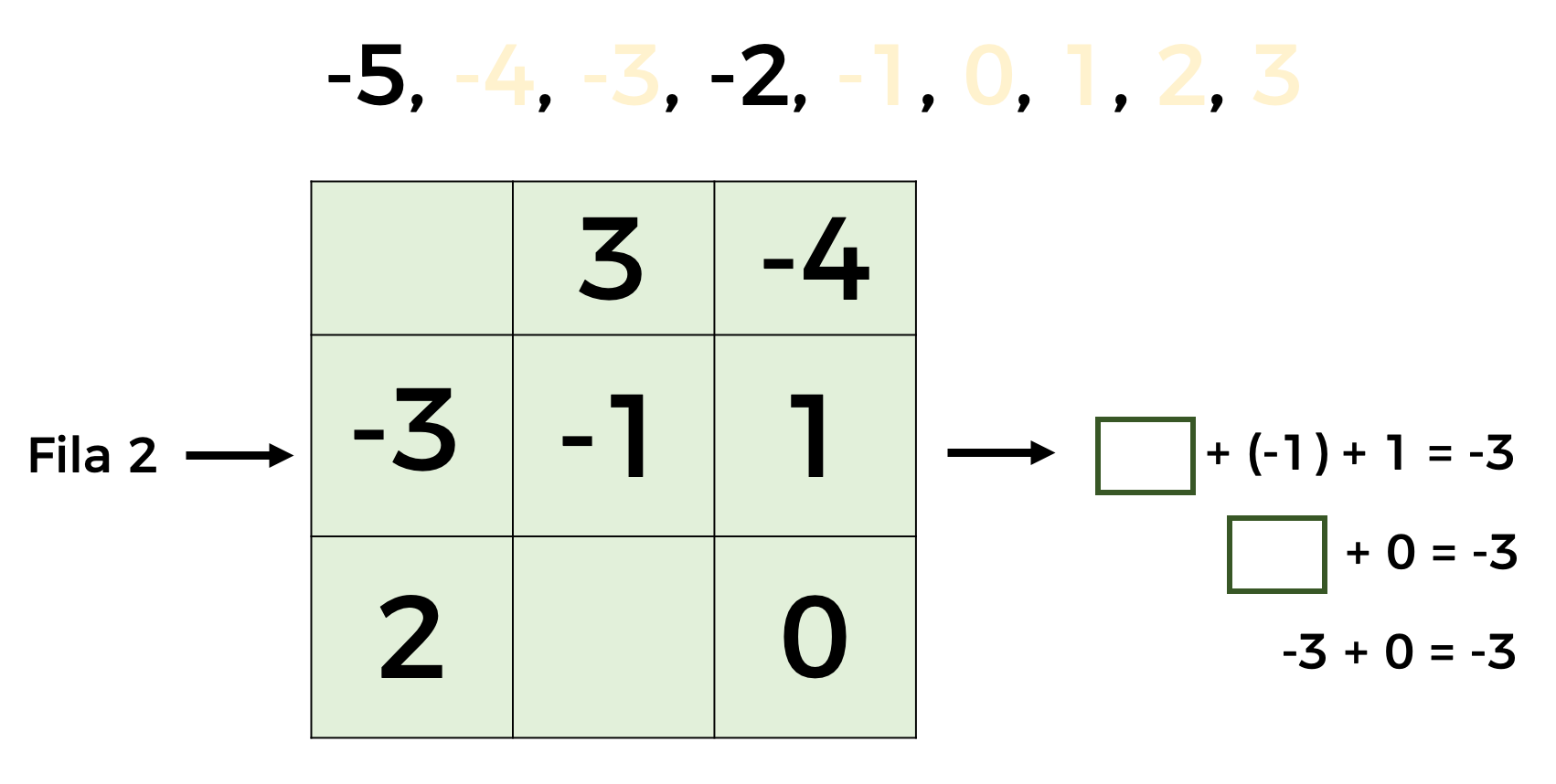
Tres negativo, ¡perfecto!

Ya solo nos quedan dos números por colocar en nuestro cuadrado mágico: cinco negativo y dos negativo; con estos números vemos cuál podemos escribir en la fila tres de tal manera que se siga cumpliendo la condición de nuestro cuadrado mágico.

Si observas con atención, al colocar el dos negativo y realizar la suma con el dos positivo y el cero no se cumple la condición del cuadrado mágico, por lo que únicamente queda colocar el número cinco negativo.
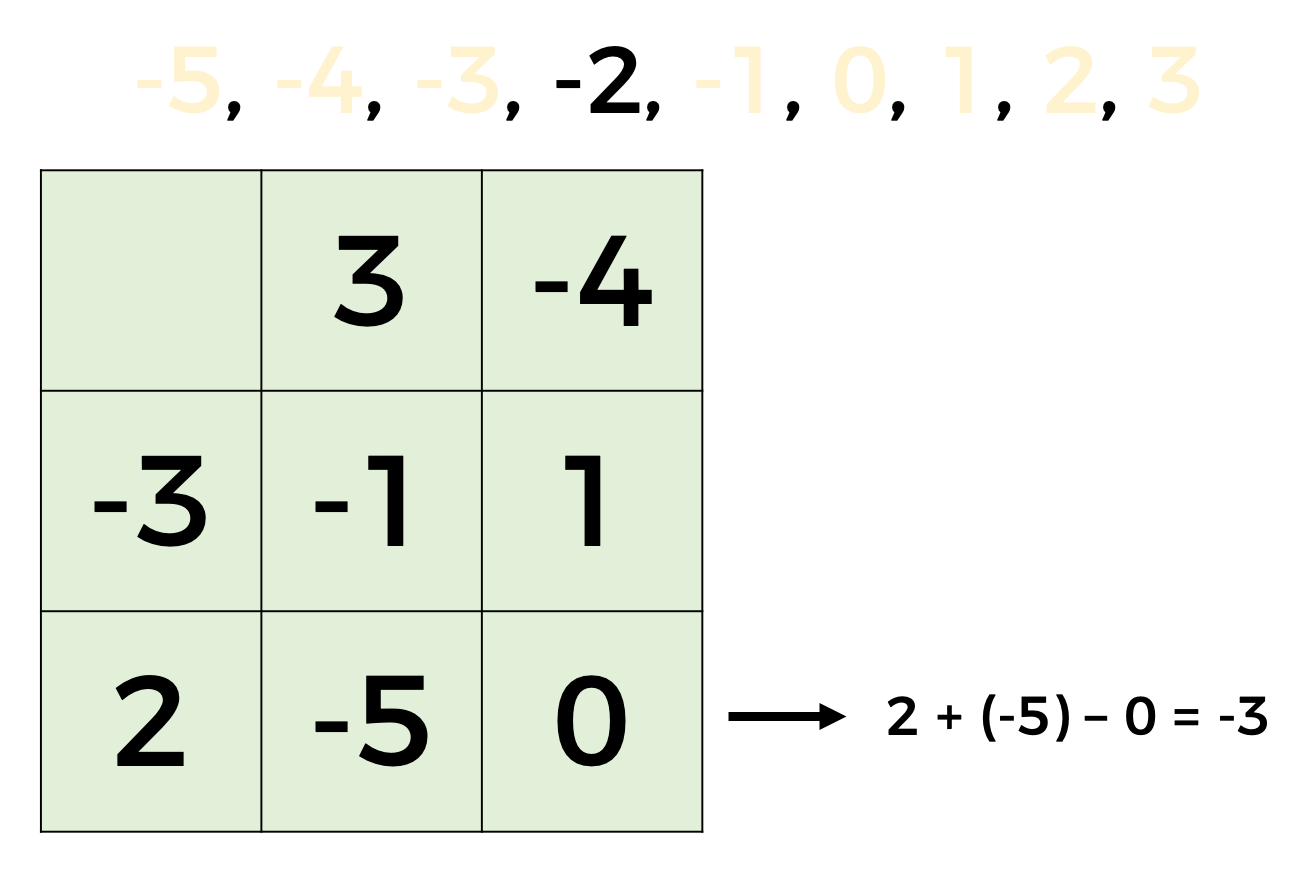
Entonces sí se cumple la condición.
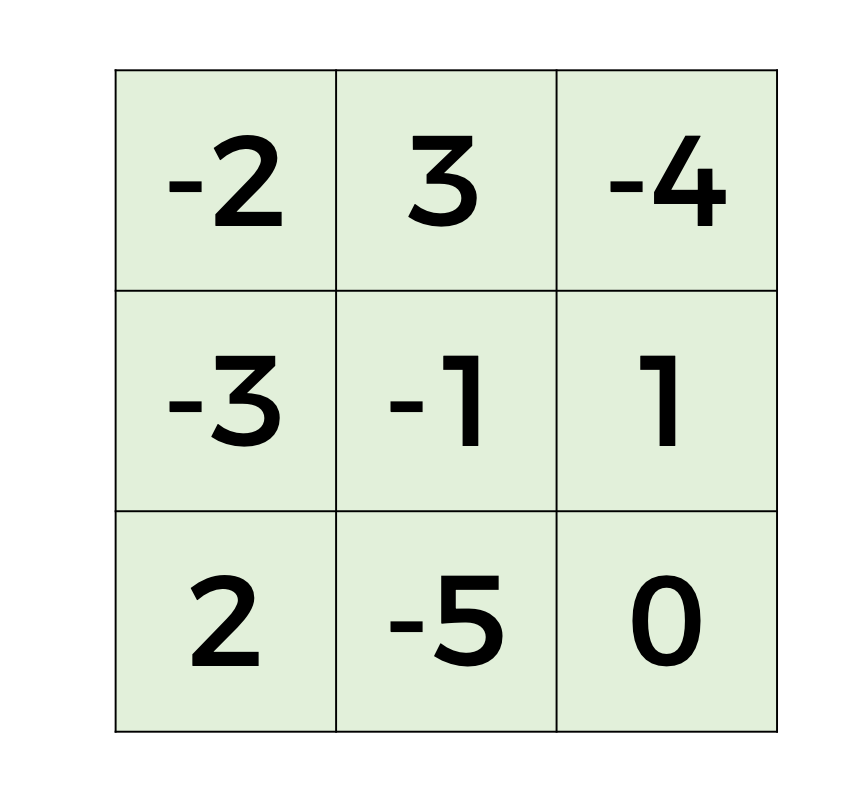
En consecuencia, el número dos negativo se escribe en el espacio del primer renglón y así concluimos con el ejercicio.
¿Te fijaste que en esta operación encontramos dos números que son simétricos?
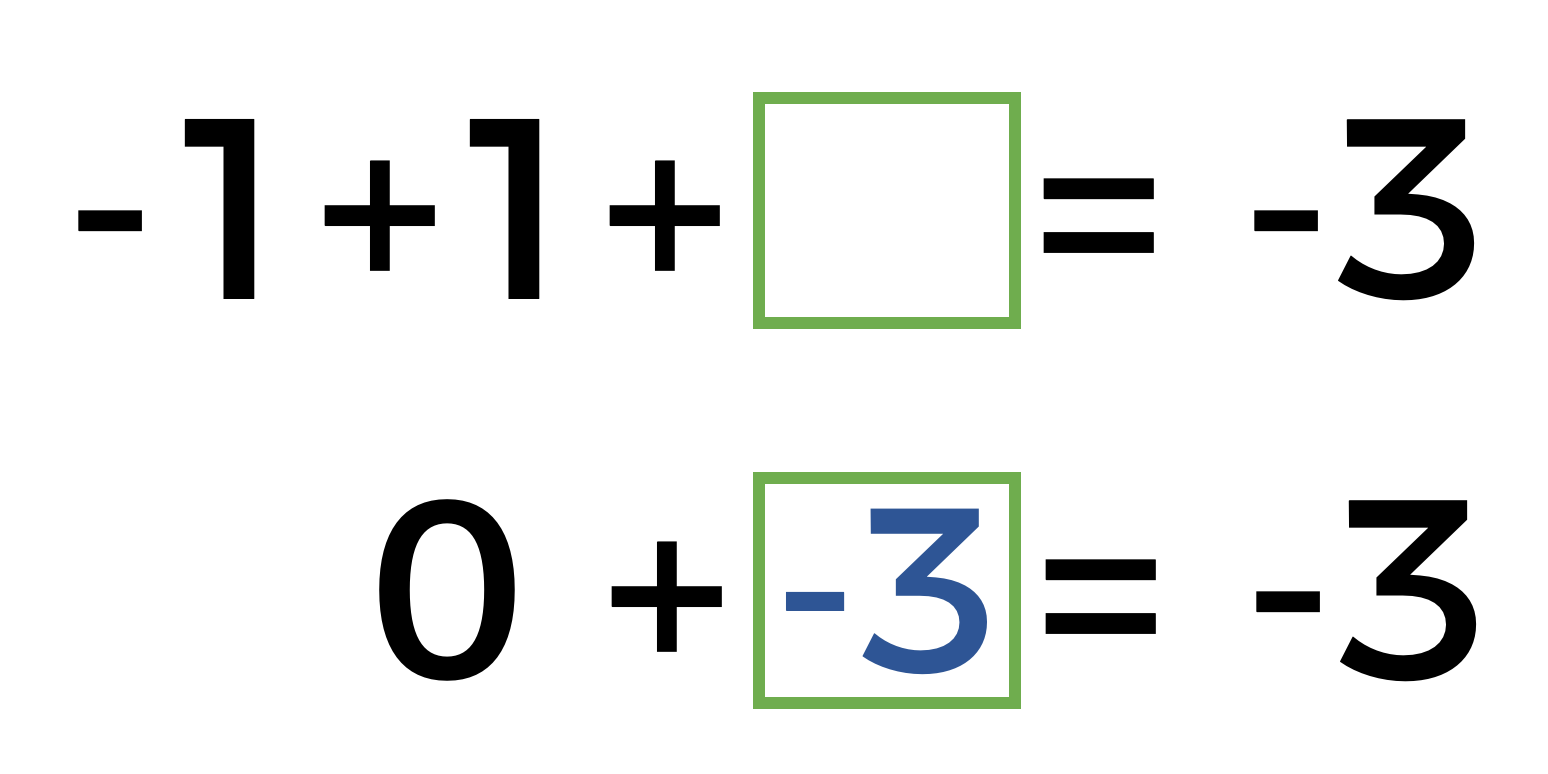
El simétrico de 1 negativo es 1 positivo, y al sumarlos el resultado es cero, de ahí entonces, el número que se debe escribir en el espacio vacío y para que se cumpla la igualdad es el número tres negativo.
Como has visto, los números positivos y negativos se pueden utilizar para describir distintas situaciones de nuestra vida cotidiana. Por ejemplo: Los negativos se emplean para representar temperaturas muy frías, mientras que los positivos para representar temperaturas más cálidas.
En el caso de los Bancos o en la administración de un negocio, los negativos representan pérdidas de dinero y deudas; mientras que los positivos representan los ingresos y ganancias.
En esta ocasión has aprendido a resolver problemas con contextos cercanos mediante la representación de los datos con números positivos y negativos. Y también a identificar el uso de estos números en la vida cotidiana.
Todo esto lo podrás aplicar en la resolución de otros problemas de matemáticas y en otras asignaturas. Así que no te olvides de ello.
Recuerda que en tu libro de texto puedes buscar el tema visto y hacer los ejercicios propuestos en él.
El reto de hoy:
Por tu cuenta, completa otro cuadrado mágico, utilizando los números de 7 negativo al 1 positivo y en donde el resultado en cada fila, columna y diagonal debe ser igual a 9 negativo.

¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas