Multiplicaciones y jerarquía de operaciones
Multiplicaciones y jerarquía de operaciones
Aprendizaje Esperado: consolida contenidos del eje: número, álgebra y variación.
Énfasis: integrar los contenidos del tema: multiplicación y división.
¿Qué vamos a aprender?
En esta sesión reconocerás las nociones y procedimientos para resolver la multiplicación de fracciones y la división de decimales; además analizarás algunos contextos en los que será necesario utilizar la jerarquía de las operaciones para obtener ciertos resultados. Profundizarás en el uso de los mismos y resolverás situaciones que puedes ubicar en tu vida cotidiana.
Se te recomienda que para el desempeño de tus actividades tengas a la mano tu cuaderno u hojas reutilizables, lápiz, goma, sacapuntas. Así como tu libro de texto de la asignatura.
En caso de tener una discapacidad visual, prepara hojas leyer, un punzón y una regleta.
¿Qué vamos a hacer?
Para iniciar, se realizará una actividad, antes de revisar el tema de esta sesión.

Para saber, debes leer detenidamente las pistas, así que recuerda que dicen así:
- Rosa dice: Marcos y yo estamos separados por una silla.
- Alex dice: Mario se sienta a mi lado.
- Carmen dice: Mi asiento es el “B”.
- Mario dice: Marcos no se sienta a mi lado.
Con estas pistas podrás saber cómo están sentados. Se te invita a establecer la silla que le corresponde a cada uno. Al final la sesión, se revisará esta actividad, para que compares tus respuestas.
Ahora, para comenzar con el tema de esta sesión, hay que recordar algunos conceptos básicos acerca de las fracciones.
En la multiplicación de dos fracciones, al realizar la operación resulta una nueva fracción cuyo numerador es el producto de los numeradores de las fracciones y su denominador es el producto de los denominadores.

Por ejemplo, la problemática anterior, se resuelve multiplicando los numeradores, se coloca como numerador de la fracción resultante, enseguida se multiplican los denominadores y el resultado se coloca como denominador de la nueva fracción, y finalmente se simplifica la fracción resultante; así se tiene que 7/8 por 5/6 es igual a 7 por 5 sobre 8 por 6 igual a 35/48. Siempre que sea posible se simplifica la fracción. Como el resultado es una fracción irreducible así se queda.

A continuación, analiza la siguiente situación donde se involucra la multiplicación de fracciones.
De un trozo de 5/6 de metro cuadrados de tela, se utilizará la mitad para hacer un mantel. ¿Cuánta tela se utilizará?
Para saber cuál es el resultado de esta situación, se utiliza una multiplicación, ya que dicha operación permite saber qué parte de una fracción representa otra fracción, en este caso 1/2 de 5/6.
5/6 por 1/2 es igual a 5 por 1 sobre 6 por 2 igual a 5/12.
Esto quiere decir que se necesitan 5/12 de metro cuadrado para hacer el mantel, que como número decimal es igual a 0.42 m2.

Ahora, revisarás cómo resolver una multiplicación entre un número mixto y una fracción.
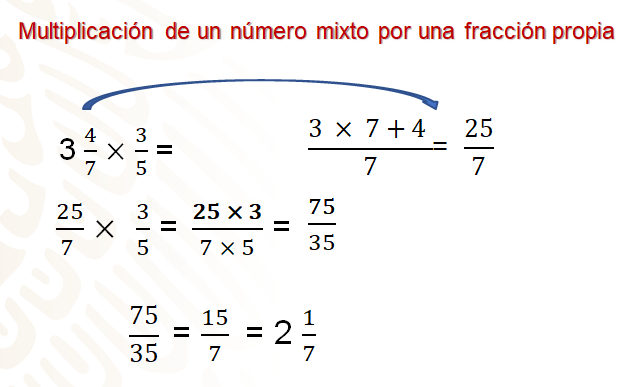
Se tiene la operación 3 4/7 por 3/5.
Primero se convierte el número mixto a fracción.
El procedimiento es el siguiente, se multiplica 3 por 7, que da 21, se le suma el numerador 4 y te da 25, por lo tanto 3 4/7 es igual a 25/7.
Así ya puedes resolver la multiplicación siguiendo las reglas revisadas, tienes entonces 25/7 por 3/5 = 25 por 3 sobre 7 por 5 igual a 75/35.
Se simplifica el resultado, para ello divides entre 5, el numerador y el denominador obteniendo 15/7 y lo conviertes a número mixto, 2 1/7.
Has reconocido los procedimientos para resolver una multiplicación de fracciones, ahora corresponde recordar el algoritmo de la división de números decimales.
Revisa el siguiente ejemplo y recuerda cómo se resuelve la división con números decimales, se usará como ejemplo la división 6.465 entre 0.15.

Observa que el divisor es un número decimal y así como está no se puede resolver la división. Pero, ¿recuerdas la propiedad de la división que viste en otras sesiones?
La cual dice: “Si en una división se multiplica el dividendo y el divisor por un mismo número se obtiene una división equivalente, es decir, el resultado no cambia”.
Para convertir 15 centésimos en 15 enteros es necesario multiplicar 0.15 por 100, entonces debes multiplicar tanto el dividendo como el divisor por 100, y como recordarás, eso equivale a mover dos lugares a la derecha el punto decimal; ahora harás lo mismo con el dividendo, después de esta conversión, la nueva división que se obtienes es 646.5 15. Por lo tanto, dividir 6.465 0.15 es igual a dividir 646.5 15.
Ya puedes resolver la división con el algoritmo que ya conoces, 15 cabe 4 veces en 64; 4 por 15 da 60, restas 64 menos 60 igual a 4, bajas el 6 con lo que ahora tu dividendo es 46, 15 cabe 3 veces en 46 entonces, 3 por 15 es igual a 45; 46 menos 45 es igual a 1, como el siguiente número por bajar es el 5, está después del punto decimal, colocas el punto en el cociente después del 43, finalmente 15 cabe una vez en 15, colocas 1 en el cociente y no sobra nada, para concluir que 6.465 entre 0.15 = 43.1.
Ahora, hay que resolver la siguiente situación problema para aplicar lo visto sobre divisiones de números decimales.
Sobre un tramo de 7.7 km de una carretera se colocaron luminarias cada 0.35 km. ¿Cuántas luminarias se colocaron en total?
Para responder la pregunta se tiene que resolver una división, 7.7 entre 0.35. Como puedes observar el divisor es un número decimal, así que debes buscar una división equivalente para que el divisor sea un número entero.
Para convertir 35 centésimos en 35 enteros es necesario multiplicar 0.35 por 100, entonces también se multiplica 7.7 por 100, así se obtiene la división 770 entre 35, que se resolverá con el procedimiento ya conocido.
Ahora ya puedes resolver la división con el algoritmo que ya conoces, para responder la pregunta del problema.
Como puedes ver, el resultado de dividir 770 entre 35 es igual a 22, por lo tanto, 7.7 entre 0.35 es igual a 22.
Ya puedes responder la pregunta, ¿cuántas luminarias se colocaron?
La respuesta es 22 luminarias.

Ya se han retomado algunos temas vistos a lo largo del ciclo escolar, conversión entre fracciones y números decimales, multiplicación de fracciones y la división de números decimales.
En casa, ¿cómo vas?
Recuerda tomar nota de los conceptos más importantes, si no has tenido oportunidad recuerda que puedes volver a ver la sesión de hoy.
Ahora, te enfocarás en las siguientes actividades en la jerarquía de operaciones. Recuerda que aplicar adecuadamente la jerarquía de las operaciones te permite obtener resultados correctos al resolver operaciones combinadas.
Como sabes, la jerarquía de las operaciones, es el orden en que deben resolverse las operaciones de un enunciado numérico.
Pero, ¿por qué se le llama enunciado numérico?
Porque sólo está constituido por una serie de números, y signos de operación que los acompaña.
Revisa cuál es el orden de ejecución:
- Primer nivel. Las operaciones dentro de paréntesis, corchetes y llaves, en ese orden.
- Segundo nivel. Exponentes y raíces, aunque en este grado (de secundaria) no se consideran este tipo de operaciones.
- Tercer nivel. Multiplicaciones y divisiones.
- Cuarto nivel. Sumas y restas.
En caso de tener que realizar operaciones del mismo nivel, se resuelven siguiendo el orden de izquierda a derecha.

A continuación, se resolverán algunos ejemplos para que quede más claro.
Se empezará con el enunciado 5 por 2 + 5.
En este caso la orden de ejecución indica que primero se debe realizar la multiplicación y al resultado se le suma cinco. Entonces cinco por dos es igual a diez y diez más cinco es igual a 15. Por lo tanto, 5 por 2 + 5 = 15.
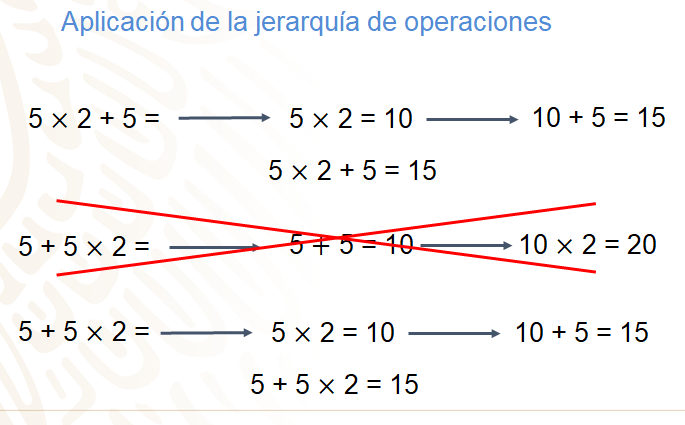
Pero, ¿qué sucede con la operación 5 + 5 por 2. ¿Ya observaste?
En este caso se presenta primero la suma, si sigues el orden en que se presentan las operaciones, primero resuelves la suma y después la multiplicación y obtendrías un resultado diferente, como puedes ver.
Por ello, es importante aplicar adecuadamente la jerarquía de las operaciones, como puedes observar, el resultado es el mismo que en la primera operación, es decir, 5 + 5 por 2 es igual a 15.
Ahora, verás otros enunciados matemáticos. Toma nota y ve resolviéndolos conforme los vas revisando aquí.
Se iniciará con la operación, 7 – 45 entre 5 + 2.
En este caso, primero se resuelve la división 45 entre 5, para obtener la operación 7 menos 9 más 2. Como la suma y la resta están en el mismo nivel, hay que resolver las operaciones de izquierda a derecha. Así tienes 7 menos 9 más 2 es igual a 2 negativo más 2 igual a cero.

Te has dado cuenta que conforme avanza el ciclo escolar, los temas se van conjuntado, en este caso también se utiliza la regla de la adición y sustracción de números positivos y negativos.
Realiza un segundo ejercicio, 2 por 6, 3 + 9. En este caso, existen dos operaciones del mismo nivel de ejecución, entonces se resolverán de izquierda a derecha, primero dos por seis es igual a doce, y se obtiene la operación 12 entre 3 + 9, a continuación, se realiza la división, doce entre tres da cuatro más nueve, por último, se realiza la adición cuatro más nueve es igual a trece.
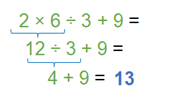
Hay que resolver otro enunciado, 4 negativo más 8 entre 4 más 5 por 3 más 2.
Como puedes observar, en este enunciado se involucran números negativos, pero primero se resuelve la división 8 entre 4 y la multiplicación 5 por 3. Al resolver queda la operación 4 negativo más 2 más 15 más 2. Como todas las operaciones están en el mismo nivel, se resuelven de izquierda a derecha, aplicando las reglas de la adición de positivos y negativos; 4 negativo más 2 más 15 más 2 es igual a 2 negativo más 15 más 2 igual a 13 más 2 igual a 15.

Ahora, hay que aplicar lo visto sobre la jerarquía de las operaciones en situaciones-problema, en las que se incluyen paréntesis.
En un huerto cierto día se recolectaron 118 manzanas, al día siguiente se recolectaron 62 manzanas más. Todas las manzanas recolectadas se guardaron en cajas con 12 piezas. ¿Cuántas cajas se llenaron?
Se te pregunta, ¿qué operación representa la situación?
Como en este caso primero tienes que sumar las manzanas que se recolectaron los dos días, para después dividir entre 12, entonces se usan paréntesis.
La operación queda, se abre paréntesis 118 + 62 se cierra paréntesis, entre 12. Primero se resuelve la suma dentro del paréntesis, 118 más 62 es igual a 180, así queda la división 180 entre 12, que es igual a 15.
Entonces se puede dar respuesta a la pregunta, se llenaron 15 cajas.

Si observas el uso del paréntesis es muy útil para unir los datos que hablan de una misma situación.
Hay que revisar otro caso.
En la tienda de don Paco había 118 botellas de aceite y llegaron 14 paquetes con 12 botellas cada uno, ¿cuántas botellas de aceite hay en total?
En este caso se debe realizar la expresión matemática con una multiplicación, para posteriormente sumar las ciento dieciocho botellas restantes. 118 + entre paréntesis 14 por 12. ¿Qué observas?
Si analizas la operación, aquí se pueden omitir los paréntesis, ya que por jerarquía primero se tiene que multiplicar 14 por 12. Entonces queda 118 más 14 por 12, que es igual a 118 más 168 igual a 286.
Así, la respuesta a la pregunta ¿cuántas botellas de aceite hay en total? es 286 botellas de aceite.

Ya viste casos en los que se utilizan los paréntesis, pero cuando se necesita agrupar operaciones que ya fueron agrupadas se utilizan los corchetes y las llaves. Para resolver una operación que tiene varios signos de agrupación, unos dentro de otros, las operaciones se llevan a cabo de adentro hacia afuera. Este proceso se conoce como “quitar paréntesis”.
Ahora, revisarás una situación problema en la que se utilizan estos signos de agrupación. Pon mucha atención.
Nicolás le regaló a su abuelita el arreglo floral que se muestra en la siguiente imagen, incluido el florero.

Si pagó con un billete de mil pesos, ¿cuánto recibió de cambio?
Observa que hay 11 rosas y que cada una cuesta 18 pesos; 6 alcatraces de 15.50 pesos, cada uno y que el florero cuesta 378.80 pesos.
¿Qué operación permite resolver el problema? ¿Cómo agruparías las cantidades para resolver el problema?
Para saber cuánto pagó se deben agrupar las operaciones por cada artículo que va a comprar 11 por 18, más 6 por 15.50, más el florero de 378.80.
Y posteriormente a mil, se le resta el resultado de sumar lo que pagó; para representar la situación se utilizarán paréntesis y corchetes.
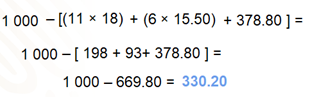
Mil menos, se abre corchete, se abre paréntesis, once por dieciocho, se cierra paréntesis, más se abre paréntesis, seis por quince punto cincuenta, se cierra paréntesis, más trescientos setenta y ocho punto ochenta, se cierra corchete.
Primero se resuelven las operaciones que se encuentran en cada paréntesis, obteniendo mil menos, se abre corchete, 198 más 93 más 378.80, se cierra corchete igual a…
A continuación, se realizan las operaciones que se encuentran dentro del corchete, 198 más 93 más 378.80 igual a 669.80.
Finalmente, se realiza la sustracción de mil menos seiscientos setenta y nueve punto ochenta, que da como resultado trescientos treinta punto veinte.
La respuesta a la pregunta ¿cuánto recibió de cambio?
Nicolás recibió trescientos treinta pesos con veinte centavos de cambio.
A continuación, se va a construir la expresión matemática de la siguiente situación.
Carlos quiere pintar su recamara rectangular de color verde, como se muestra en la siguiente imagen.
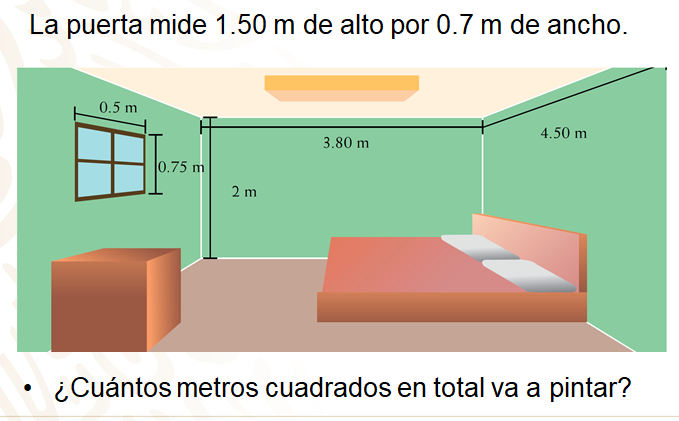
En la pared que no se ve, está la puerta, que mide 1.50 m de alto por 0.7 m de ancho. ¿Cuántos metros cuadrados en total va a pintar Carlos?
¿Ya sabes cómo resolver el problema?
Para responder, tienes que calcular el área de todas las paredes y al resultado restarle el área de la puerta y la ventana, ya que esas partes no las va a pintar.
¿Qué operaciones se requieren y qué signos de agrupación usarías?
El enunciado matemático que representa la situación es, abres llave, anotas el número 2, que multiplicará a las medidas de las paredes, ya que al ser rectangular, tiene dos paredes con las mismas medidas; entonces abres corchete, abres paréntesis, dos por cuatro punto cincuenta, se cierra el paréntesis; más, se abre paréntesis, dos por tres punto ochenta, se cierra paréntesis, se cierra corchete, y se cierra llave; a lo anterior, se le resta la medida de la puerta y la ventana, entonces todo lo anterior, menos, se abre corchete, se abre paréntesis, cero punto cinco por cero punto setenta cinco, se cierra paréntesis, más, se abre paréntesis, uno punto cinco por cero punto setenta y cinco, se cierra paréntesis, y se cierra corchete.
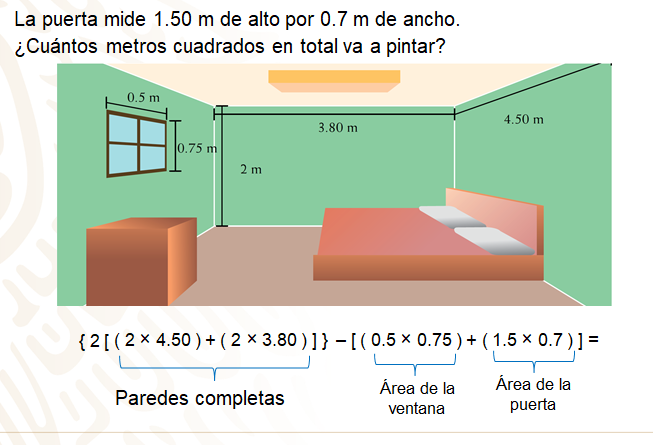
Hay que resolver el enunciado matemático del problema. Se iniciará por resolver las operaciones; recuerda que cuando se tienen varios signos de agrupación, las operaciones se resuelven de adentro hacia afuera.
Así que, se abre llave, se anota el dos, se abre corchete, se realiza la multiplicación de dos por cuatro punto cinco, obteniendo nueve, más dos por tres punto ochenta da siete punto seis, se cierra corchete, y se cierra llave, menos, se abre corchete cero punto cinco por cero punto setenta y cinco, da cero punto trescientos setenta y cinco, más uno punto cinco por cero punto setenta, da uno punto cero cinco, se cierra el corchete.

Ya se realizaron las operaciones que se encontraban entre paréntesis, ahora se eliminan los corchetes. ¿Cómo? Pues realizando las operaciones que hay dentro de ellos.
Se abre llave, se anota dos, se abre corchete nueve más siete puntos seis, da dieciséis punto seis, se cierra corchete, menos cero punto trescientos setenta y cinco, más uno punto cero cinco, da uno punto cuatrocientos veinticinco igual a…
Antes de ver qué resultado da, responde la siguiente pregunta: ¿qué observas entre el número dos y el corchete?
Como puedes ver, no hay un signo, lo que indica que el dos va a multiplicar a lo que está dentro del corchete de la siguiente manera, dos por dieciséis punto seis da treinta y tres punto dos menos uno punto cuatrocientos veinticinco es igual a…
Finalmente se realiza la sustracción del total de pared menos el total del área de la puerta y ventana, obteniendo treinta y tres punto dos menos uno punto cuatrocientos veinticinco, es igual a treinta y uno punto setecientos setenta y cinco metros cuadrados, que es lo que Carlos tendrá que pintar en su recámara.
Con este ejercicio se ha concluido el tema de esta sesión.
Ahora, hay que regresar al problema que se vio en un inicio de la sesión. ¿Recuerdas?
Vas a ver cómo están sentados los amigos de Marcos.
Rosa indica que Marcos y ella están separados por una silla, lo que indica que Rosa ocupa la silla “A” y Marcos la silla “C”.
Carmen indica que su silla es la “B”, hasta ahora ya sabes que están ocupadas las sillas “A”, “B” y “C”.
Alex indica que Mario se sienta a su lado, hay dos alternativas la silla “D” y “E”; para saber, debes leer lo que da a conocer Mario, él dice que no se sienta junto a Marcos, recuerda que Marcos está sentado en la silla “C”, como Mario no está sentado a su lado te indica que está en la silla “E” y que Alex está en la silla “D”.

Se espera que hayas tenido los mismos resultados.
El reto de hoy:
Si tienes alguna duda o inquietud, revisa tu libro de texto, en la parte donde aparece el Aprendizaje Esperado de esta sesión, de igual forma puedes recurrir a tu profesora o profesor de esa asignatura para que te apoyen.
Concluye los ejercicios realizados en el desarrollo de la sesión, en caso de que aún te falte alguno por realizar o terminar.
¡Buen trabajo!
Gracias por tu esfuerzo.
Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas