Multiplicación de fracciones por decimales
Multiplicación de fracciones por decimales
Aprendizaje esperado: resuelve problemas de multiplicación con fracciones y decimales y de división con decimales.
Énfasis: resolver problemas con multiplicación de fracciones y números decimales.
¿Qué vamos a aprender?
Durante esta sesión aprenderás a resolver problemas que implican la multiplicación de fracciones y números decimales.
¿Qué hacemos?
Se iniciará esta sesión con un ejemplo de un juego lógico matemático.
Eva tiene 5 dados de diferente color, pero iguales; y acomoda tres dados, uno sobre otro y le pregunta a Hugo: ¿cuánto suman las caras que no se pueden ver?, es decir, la de abajo y las cuatro ocultas por el acomodo de los dados.
Hugo responde que no sabría que responder, pues las caras no se ven.
Pero Eva le dice que suman 16.
Hugo pregunta: ¿qué cómo lo supo?
Eva dice que colocará un dado más y ocultará lo que parece ser la clave para conocer la suma sugerida. Y le pregunta a Hugo si ¿podría decir cuánto suman las caras que no se ven? Únicamente considerando el número visible.
Hugo responde: que ahora menos, que si ella si sabe.
A lo que Eva dice que, la suma sería 25, y lo comprueba. Al finalizar esta sesión, se darán algunas pistas a considerar para dar solución a este juego.
Ahora, después de leer el juego, se revisará el siguiente problema.
Mariana decidió comprar chocolates para compartir con sus amigos. La tienda ofrece los siguientes precios por kilogramo de chocolate: Chocolate con leche: noventa y siete pesos con veinte centavos. Chocolate amargo: ciento cuarenta y cinco pesos con cuarenta centavos. Chocolate con nuez: ciento treinta pesos con cincuenta centavos. Y chocolate mixto: setenta y ocho pesos con setenta y cinco centavos.

Mariana decidió comprar un cuarto de kilogramo de chocolate con leche, medio kilogramo de chocolate amargo, un quinto de kilogramo de chocolate con nuez y cuatro tercios de kilogramo de chocolate mixto.
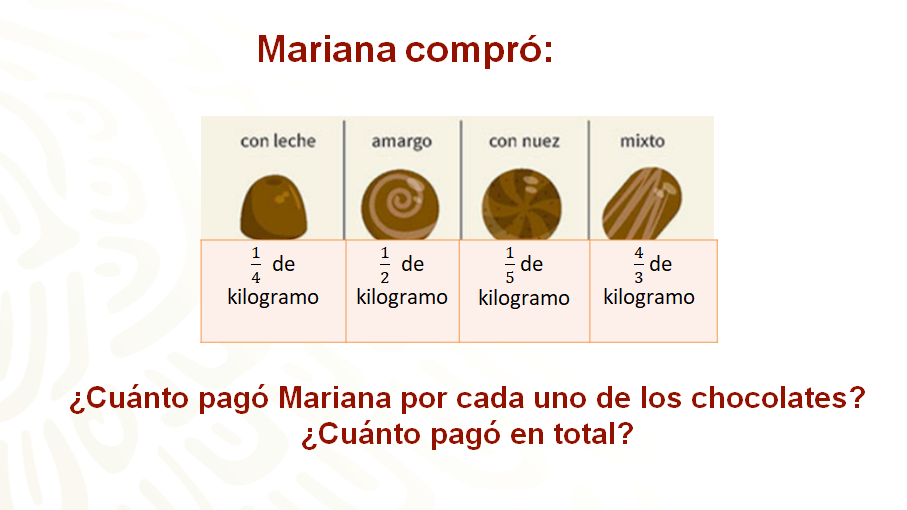
Antes de resolver el problema, observa el siguiente audiovisual que te ayudará a identificar el tipo de fracciones y números decimales mencionados en el problema.
- Tipos de fracciones y decimales.
https://www.youtube.com/watch?v=CDnq-63F_Tg&feature=youtu.be
¿Lograste identificar el tipo de fracciones y números decimales que se mencionan en el problema?
Ten a la mano tus respuestas porque te servirán para organizar la información del problema.
Conoces los costos de cada tipo de chocolate, los cuales están expresados en números decimales, y las cantidades que Mariana va a comprar están expresadas en fracciones, presentadas en una tabla. Estas cantidades se representan, en su mayoría, por una fracción unitaria, y uno de los datos está representado por una fracción impropia.
¿Cuál será el procedimiento adecuado para resolver el problema?
Analiza el primer caso, variando la cantidad que se compra del chocolate con leche, para observar cómo se comportan los costos por kilogramos comprados.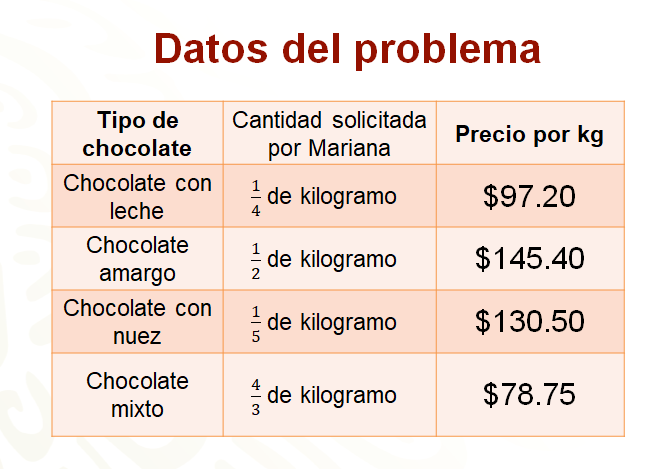
En la tabla anterior, se muestran las variaciones en la cantidad de kilogramos de chocolate de leche por comprar. La cantidad puede variar, mientras que el precio es constante, es decir, no cambia.
Para solucionar el problema se utilizará el algoritmo de la multiplicación; en este caso, los factores del producto son fracciones y números decimales.
Se puede expresar la multiplicación con paréntesis o con el signo de por. Para este caso se usarán los paréntesis. La tabla muestra el costo total para diferentes cantidades de chocolate de leche: un cuatro, un medio, tres cuartos, un kilogramo, cinco cuartos y tres medios de kilogramo.
¿Cómo puedes obtener el costo en cada caso?
Considera que se quieren comprar tres cuartos de kilogramo de chocolate de leche, para conocer el costo, se multiplican tres cuartos por 97.20.
Es preciso mencionar que el orden de las operaciones no altera el producto, es decir, el resultado de la multiplicación.
Puedes dividir noventa y siete punto veinte entre cuatro, que da como resultado veinticuatro punto treinta; después, multiplicar por tres para obtener como resultado final setenta y nueve pesos con noventa centavos, que es lo que se pagaría por tres cuartos de kilogramo de chocolate de leche.
También se puede multiplicar noventa y siete punto veinte por tres y el resultado es doscientos noventa y uno punto sesenta, y, por último, dividir entre cuatro. En ambos casos se obtiene como resultado setenta y dos pesos con noventa centavos.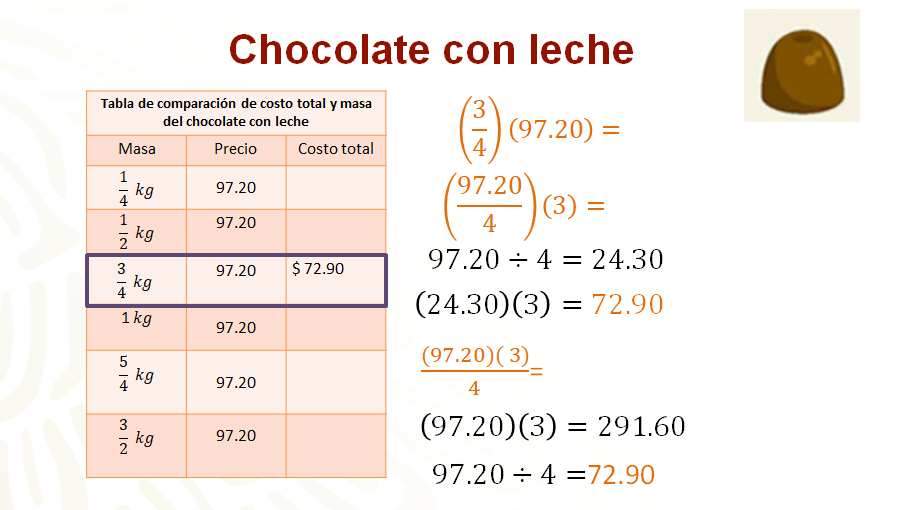
Si observas, ambos resultados son iguales, aunque el orden de las operaciones fue distinto. A esta propiedad se le conoce como propiedad conmutativa de la multiplicación, en donde el orden de los factores no altera el producto.
Ahora se te invita a completar los resultados de la tabla elaborada siguiendo los procedimientos sugeridos para multiplicar fracciones y números decimales.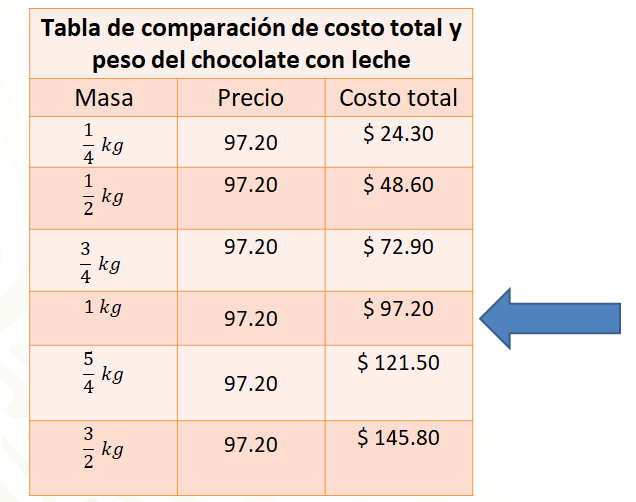
Por medio kilogramo de chocolate de leche se pagan 24.30 pesos; por medio kilogramo, 48.60 pesos; por cinco cuartos, 121.50 pesos, y por 3 medios, 145.80 pesos.
Observa que, si la fracción es propia, el costo total del chocolate disminuye precisamente por ser menor a la unidad establecida, y si la fracción es impropia, es decir, mayor a la unidad, el costo total también aumenta. En casa resuelve las operaciones paso a paso para verificar los resultados que muestra la tabla.
Siguiendo los procedimientos aprendidos, se dará respuesta a las preguntas del problema inicial sobre lo que pagó Mariana en cada caso. Para lograrlo, se multiplica la cantidad solicitada, representada como fracción, por el precio de cada chocolate, expresado en número decimal. Observa los resultados: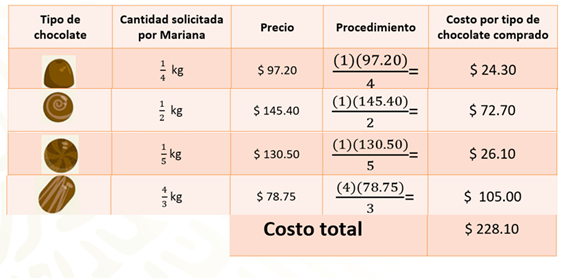
En la tabla se muestra cada una de las operaciones realizadas para obtener el costo por tipo de chocolate comprado y el costo total de la compra completa. Realiza los procedimientos correspondientes.
Para el caso del chocolate de leche, se multiplica uno por noventa y siete punto veinte entre cuatro, da como resultado veinticuatro pesos con treinta centavos.
Para el chocolate amargo, uno por ciento cuarenta y cuatro punto cuarenta entre dos, resultan setenta y dos pesos con setenta pesos.
Para el chocolate de nuez, compró un quinto, lo que es igual a uno por ciento treinta punto cincuenta entre cinco, da como respuesta veintiséis pesos con diez centavos.
Y finalmente, para el chocolate mixto se multiplica cuatro por setenta y ocho punto setenta y cinco, entre tres, resultan ciento cinco pesos.
Para concluir el problema, sólo falta sumar todos los resultados obtenidos, es decir:
Veinticuatro pesos con treinta centavos, más setenta y dos pesos con setenta centavos, más veintiséis pesos con diez centavos, más ciento cinco pesos es igual a doscientos veintiocho pesos con diez centavos. Con esto ya sabes lo que pagó Mariana por los chocolates que compró.
Observa cómo los procedimientos que aprendiste te pueden ayudar con diversas situaciones, como la siguiente:
El reto en esta ocasión será saber cuánta agua hay en el tinaco después de ciertos periodos de tiempo. Por ejemplo, en 0.5 segundos, en 1.2 y en 3.4 segundos. ¿Cómo puedes obtener las respuestas?
¿Qué cantidad de agua hay en el tinaco en cero punto cinco, uno punto dos y tres punto cuatro segundos?
Para resolver este problema puedes recurrir al procedimiento previamente aprendido, pero primero identifica los datos del problema.
Se conoce la razón constante del problema: nueve quintos de litro; el tiempo será la variable por considerar mientras se mantenga la llave abierta.
La siguiente tabla muestra las variaciones que se pueden tener respecto al tiempo de apertura de la llave.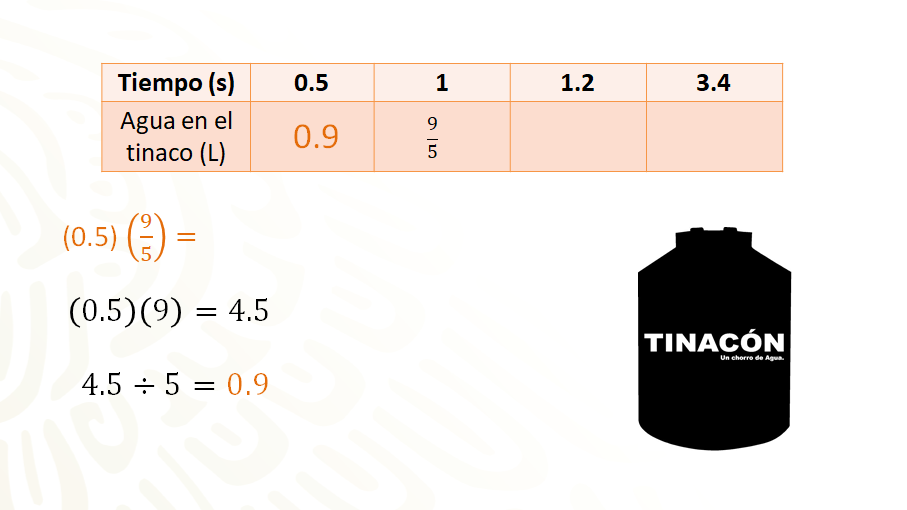
La primera fila muestra el tiempo expresado en números decimales. Mientras que la segunda fila muestra los litros de agua en el tinaco según el tiempo correspondiente.
El procedimiento que aprendiste te permite multiplicar un número decimal por una fracción de la siguiente manera:
Se multiplica cero punto cinco por nueve quintos, que es la constante del problema. Para desarrollar el procedimiento, se multiplican los factores cero punto cinco por nueve, resulta cuatro punto cinco. Posteriormente, dicho resultado se divide entre cinco, se obtiene como resultado cero punto nueve, que es la cantidad de agua, en litros, que cae al tinaco en cero punto cinco segundos.
Se te invita a encontrar los valores faltantes utilizando el procedimiento de tu preferencia.
Si realizaste correctamente todo tu procedimiento, obtendrás los siguientes resultados.
En 1.2 segundos el tinaco tendrá 2.16 litros de agua, y en 3.4 segundos, 6.12 litros.
Pero ¿consideras más adecuado que los resultados obtenidos sean expresados en fracciones?
Así es, debes unificar todas las respuestas. Observa los procedimientos que debes de seguir para realizar la conversión correspondiente. - Conversiones.
https://www.youtube.com/watch?v=0sj0z33Jzss&feature=youtu.be
Revisa del tiempo 03:30 al 04:33.
Aplica estos procedimientos con los datos del problema.

El primer resultado corresponde a cero punto nueve, expresado en fracción decimal, es nueve décimos debido a que hay una posición después del punto decimal; como denominador sólo debes colocar la potencia de diez con la misma cantidad de posiciones, en este caso, sería diez. La fracción decimal nueve décimos no tiene un divisor común para su reducción, por lo tanto, la fracción se queda de esa manera.
En la tercera opción se tiene como resultado dos punto dieciséis, expresado en su forma decimal como dos enteros dieciséis centésimos. Debido a que hay dos posiciones después del punto decimal, como denominador sólo debes colocar la potencia de diez, en este caso, sería cien. La fracción decimal es doscientos dieciséis centésimos, para este caso, el divisor común es dos; al dividir doscientos dieciséis entre dos da como resultado ciento ocho, y al dividir cien entre dos da como resultado cincuenta. Nuevamente aplicas como divisor común el dos para obtener como resultado noventa y cuatro veinticincoavos. Ahora ya no tienes un divisor común que pueda ser aplicado para el numerador y el denominador, por lo tanto, la fracción final queda como cincuenta y cuatro veinticincoavos; se puede resolver la división de la fracción impropia, obteniendo de esta forma dos enteros y cuatro veinticincoavos, conocido como un número mixto.
En el último ejemplo está el número decimal tres punto cuatro, expresado en fracción decimal como treinta y cuatro décimos. Debido a que hay una posición después del punto decimal como denominador, sólo debes colocar la potencia de diez con la misma cantidad de posiciones después del punto decimal, en este caso, sería diez. La fracción decimal queda expresada como treinta y cuatro décimos, tiene como divisor común el número dos. La reducción correspondiente queda como diecisiete quintos; ambos, al ser números primos diferentes, no tienen más reducciones, por lo tanto, esta es la fracción final. También se puede resolver la división de la fracción impropia, queda el número mixto tres enteros dos quintos.
Has acomodado los resultados que se obtuvieron en una tabla que contiene las fracciones propias e impropias como solución.
Es hora de que reflexiones sobre los problemas que has aprendido en esta sesión.
Es necesario tener presente que los procedimientos para la resolución de algún problema no están estandarizados para ocupar los mismos en todos los problemas.
Tú puedes ocupar el procedimiento que más se te facilite para llegar a la solución.
Aquí se utilizó la conversión de decimal a fracción para unificar la solución, pero se puede reproducir este procedimiento al inicio de los problemas para obtener el producto con factores decimales o con fracciones, y posteriormente realizar la multiplicación correspondiente.
Si un procedimiento válido te ayuda a encontrar la solución, puedes utilizarlo.
Ahora se resolverá el siguiente problema.
Pablo entrena todos los días en una pista que mide 1.35 km de longitud. Él lleva un registro de las vueltas que le da a la pista cada día para, posteriormente, determinar la distancia que recorre.
Como ya viste, la pista mide 1.35 km de longitud, y el día lunes Pablo le dio 2 vueltas y tres cuartos; el martes, tres vueltas y media; el miércoles, una vuelta y cuatro quintos; el jueves, dos vueltas y dos tercios, y el viernes, cuatro vueltas un cuarto.
¿Cómo puedes saber la distancia que recorrió Pablo cada día?
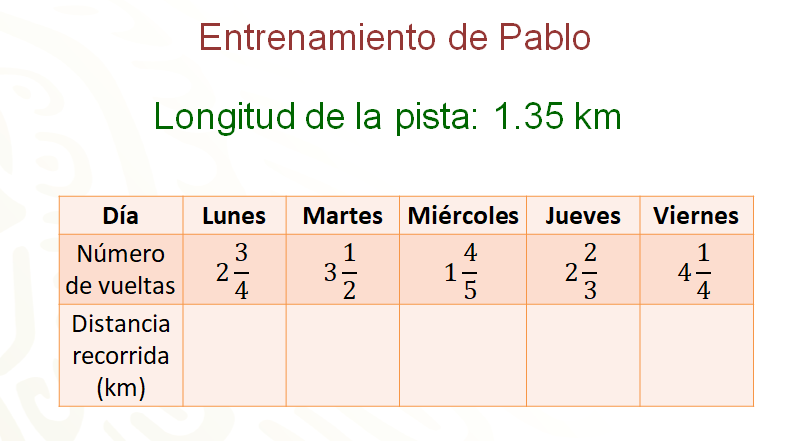
Para completar la tabla, se deben resolver las operaciones siguiendo el procedimiento visto a lo largo de esta sesión: multiplicarás un número decimal por una fracción. En este caso, lo primero que se hará, será convertir los números mixtos en fracciones.
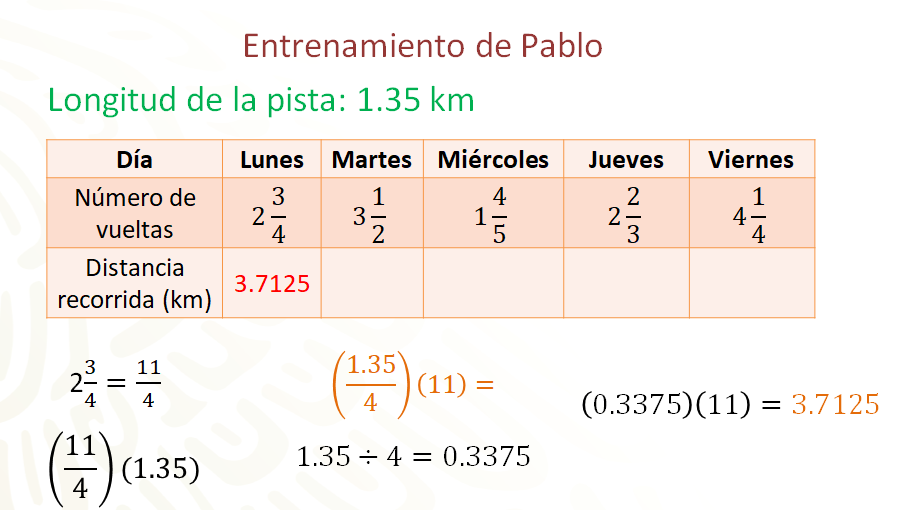
El lunes le dio 2 vueltas y tres cuartos; se convierte 2 enteros tres cuartos a fracción, obteniendo como resultado once cuartos. Y se resuelve la multiplicación 11 cuartos por uno punto treinta y cinco. Divides 1.35 entre 4, que es igual a 0.3375, y este resultado se multiplica por 11, se obtiene 3.7125, que son los kilómetros que recorrió Pablo el día lunes.
En casa, ¿conoces otro procedimiento?
Existen diferentes formas de resolver este tipo de operaciones, convertir a fracciones y resolver una multiplicación de fracciones, o también se puede operar con números decimales.
Para obtener la distancia que recorrió el martes, se operará con las fracciones. 3 enteros y un medio es igual a siete medios y 1.35 es igual a 135 centésimos. Ahora se multiplica siete medios por 135 centésimos, aplicando el procedimiento numerador por numerador y denominador por denominador; el resultado es 945 doscientosavos. Y para convertir a número decimal, se divide 945 entre 200, que es igual a 4.725. Así se sabe que Pablo corrió 4.725 kilómetros el día martes.
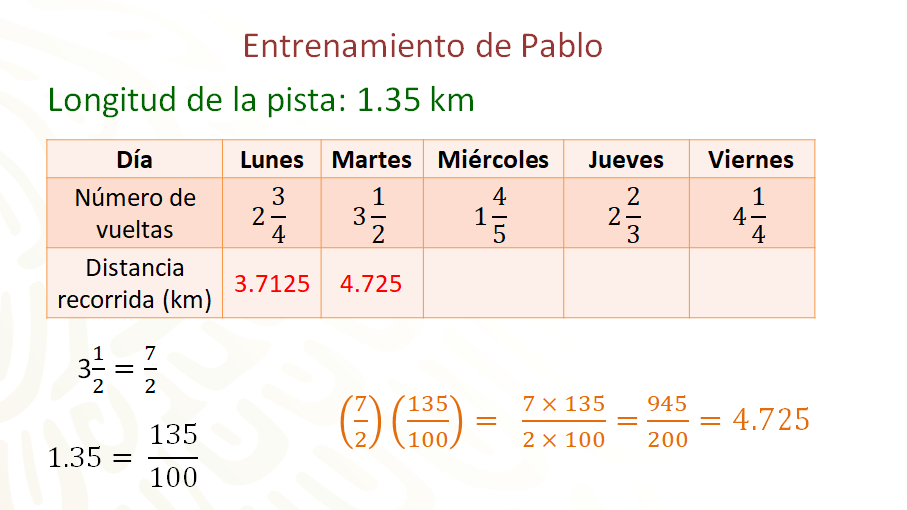
Para el día miércoles, se va a resolver operando con números decimales. Se convierte un entero cuatro quintos a la fracción nueve quintos, y se divide el numerador entre el denominador para convertir a número decimal, así se tiene que nueve quintos es igual a 1.8. Se multiplica 1.35 por 1.8, se opera como si fueran números naturales y en el resultado se consideran tantas cifras decimales como cifras decimales tengan los dos factores, que en este caso son tres. Así se tiene que 1.35 por 1.8 es igual a 2.43, que representa los kilómetros que corrió Pablo el día miércoles.
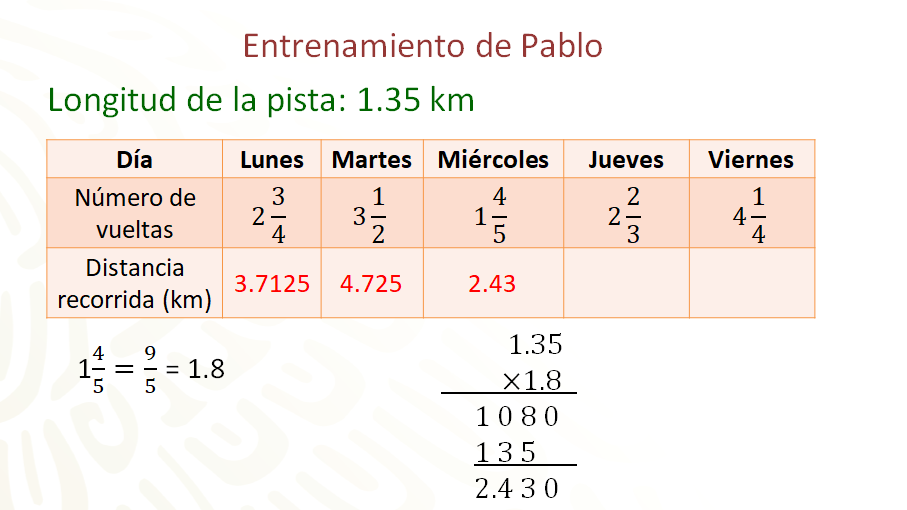
Ya únicamente falta conocer la distancia que recorrió Pablo los días jueves y viernes, ¿cuál de los procedimientos vistos te parece más adecuado? ¿Cuál usarías para cada día?
Bien, para el caso del jueves, como 2 enteros dos tercios no tiene un número decimal finito equivalente, ya que su representación decimal es 2.66 infinito, en ese caso es mejor operar con fracciones, y para el día viernes, que son cuatro vueltas y un cuarto, se puede utilizar cualquiera de los procedimientos vistos.
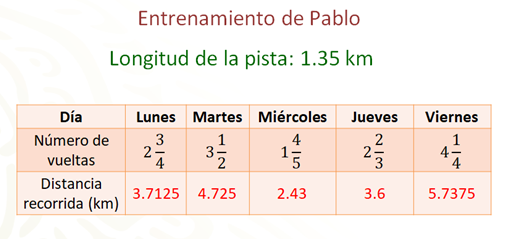
Entonces, después de resolver las operaciones, se tiene que Pablo corrió 3.6 kilómetros el día jueves y 5.7375 kilómetros el día viernes. En casa copia los resultados de la tabla, y en cada caso utiliza los distintos procedimientos que se utilizaron y valida los resultados.
Para concluir, retomando el ejemplo del juego de los dados del inicio de la sesión se te darán algunas pistas. Como sabes, todos los dados vienen numerados del 1 al 6, al ser todos iguales deberás observar con detenimiento la forma como se están sumando los lados del dado. Cuando entiendas el porqué, serás capaz de replicar el juego con amigos y familiares y sorprenderlos con tus nuevos conocimientos adquiridos.
El reto de hoy:
Revisa en casa tu libro de texto y busca el aprendizaje esperado de esta sesión, ahí revisa el tema del día hoy.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/