Multiplicación con fracciones
Multiplicación con fracciones
Aprendizaje esperado: resuelve problemas de multiplicación con fracciones y decimales y de división con decimales.
Énfasis: resolver problemas de multiplicación con fracciones.
¿Qué vamos a aprender?
En esta sesión continuarás con el estudio del aprendizaje esperado: “Resuelve problemas de multiplicación con fracciones y decimales y de división con decimales”.
Para ello, resolverás problemas en donde utilizaremos la multiplicación de fracciones.
Recuerda tener a la mano que vas a utilizar en la sesión:
- Cuaderno de matemáticas o papel para escribir.
- Lápiz.
- Colores, los cuales pueden utilizar para señalar o identificar lo que consideren más importante durante el desarrollo de la lección.
- Y su libro de texto de Matemáticas.
Hacer anotaciones te ayudará a reflexionar y a analizar el contenido que estudiaremos, y posteriormente podrán consultar y apoyarse con la información de su libro de texto.
Es importante comentar sobre un método antiguo para multiplicar fracciones. Éste fue utilizado por algunas culturas precolombinas en nuestro país, las cuales hacen referencia a una leyenda de una población denominada Acajay, pertenecientes a la provincia de Nanipiaca. Ellos eran expertos en hacer mediciones utilizando partes de su cuerpo, como manos, brazos y codos; así como objetos de uso cotidiano, por ejemplo, las varas de caña. Por lo que utilizaban dichos implementos para tomar mediciones, aunque por la diferencia en los tamaños, no siempre obtenían las mismas medidas.
Fue Numa, una mujer de la población, a quien se le ocurrió una manera sistemática de elaborar varas para hacer mediciones.
Cortaban una vara de cierta medida que representaba una unidad, a partir de ésta cortaba otras varas. Cuando la vara “unidad” no alcanzaba a medir algo, utilizaba una caña que media un medio de vara, llamada oticaimo, que quiere decir, pequeño de a 2. Como muestra la imagen, si ésta no alcanzaba para medir, utilizaba una que medía 1/3 de vara, también podían hacerse varas de un cuarto, un quinto, un sexto y así sucesivamente.
Este sistema de Numa resultó muy útil para los acajay, ya que les permitía hacer mediciones con mayor precisión, incluso hacían operaciones fraccionarias como ellas.
¿Qué hacemos?
Observa la siguiente problemática
“La amiga de Nadie quiere hacer galletas de chocolate, pero la receta es para hacer 30 piezas, y sólo quiere preparar una tercera parte de las porciones indicadas en la receta, cuyos ingredientes son los siguientes:”
- Harina: 3/4 de kilogramo
- Cocoa: 2 tazas
- Mantequilla: 1 barra
- Leche condensada: 1/ 2 lata
Hay que determinar qué procedimiento debe seguir la amiga de Nadia, para esto te puedes apoyar en el recurso que retoma el principio de la “Vara de los Acajay”. ¿Qué te parece si comenzamos con la leche condensada y así calculamos la tercera parte de media lata? de la siguiente forma:
Dibuja 6 varas subdividiéndolas por medio de una marca en proporciones iguales, comenzando en una subdivisión, dos, tres y así sucesivamente hasta llegar a 6 partes iguales. Sólo que esa última la vas a colorear de rojo, aquí cabe hacer una pregunta: ¿a cuántos sextos equivale un entero?
Seis sextos son igual a un entero, tal y como lo indica la imagen:
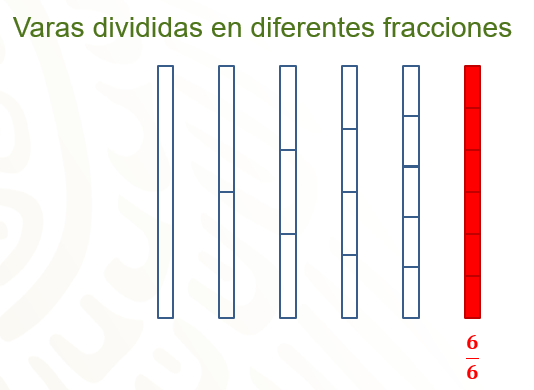
Entonces un medio, que es la medida de leche condensada que indica la receta, equivale a 3 sextos. En este caso están sombreadas solamente tres subdivisiones, lo cual indica que tres sextos equivalen a un medio de vara.
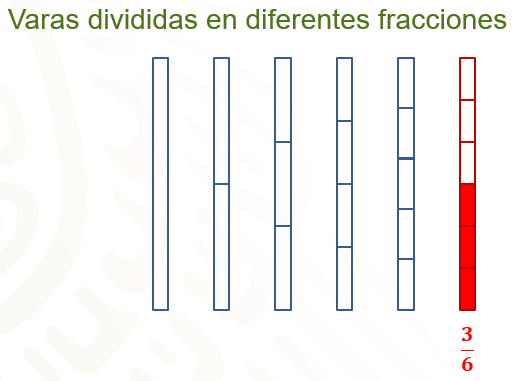
Entonces, si un medio es igual a tres sextos, se sombrea de color azul la segunda vara que representa la mitad y se concluye lo anterior.
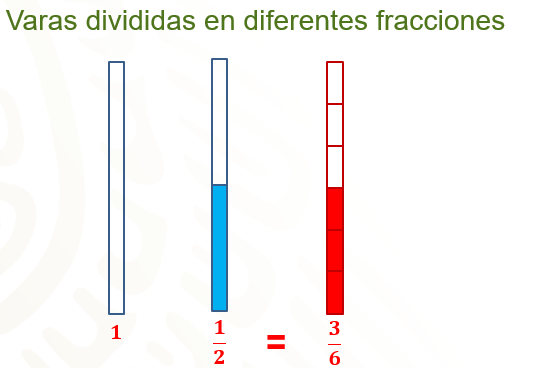
Entonces a partir de lo que acabas de ver, ya puedes establecer cuánto es un tercio de un medio de lata de leche condensada, es decir, cuánto es una tercera parte de tres sextos.
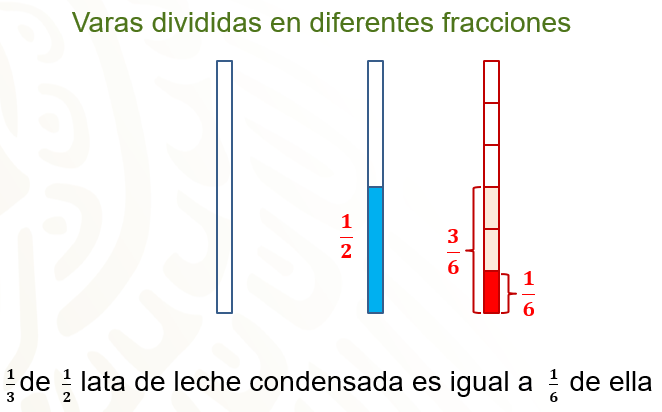
Considerando las tres partes sombreadas en rojo, si seleccionas una de esas partes: es decir, una tercera parte de ellas, esta representa un sexto de vara, como podemos observar. Así puedes determinar que un tercio de un medio de lata de leche condensada es igual a un sexto de ella.
Para conocer qué fracción representa una fracción de otra, como fue el caso anterior, lo que puedes hacer es resolver una multiplicación de fracciones. Pero, a través de la técnica de los Acajay pudiste justificar el método que ya conocemos y que consiste en multiplicar el numerador por numerador, y posteriormente hacer el producto de los denominadores.
Si aplicas el método conocido para corroborar qué fracción de un medio representa un tercio, multiplica uno por uno igual a uno y dos por tres, que es igual a 6, así podemos ver que 1/2 por 1/3 es igual a un sexto.
Entonces mediante una multiplicación de fracciones se puede determinar la cantidad de harina, de cocoa y de mantequilla que requiere la amiga de Nadia para elaborar las 10 galletas. Como lo muestra la siguiente imagen:

En el caso de la harina para 30 piezas se requieren 3/4 de kg; por lo tanto, para 10 piezas multiplica 3/4 por 1/3, que es igual a 3/12 de kg de harina.
Para la cocoa multiplica 2 enteros por 1/3, en este caso representa a 2 como una fracción con denominador uno; por lo tanto, 2 por 1/3 o es igual a 2/3 de taza de cocoa.
En el caso de la mantequilla es un entero por una fracción siendo el producto de 1 por 1/3, lo cual es igual a 1/3 de barra.
Y en lo referente a la leche condensada que ya vimos, 1/2 por 1/3 es igual a un sexto de lata.
Toma nota del siguiente ejemplo:
“Abel compró leche en una jarra con capacidad máxima de 3.5 litros. Si se llenó a tres quintas partes de su capacidad, ¿qué cantidad de leche contiene la jarra?”
En este caso la forma adecuada para resolver lo anterior implica una multiplicación. Pero en este caso observa que tenemos una fracción y un número decimal; ¿podemos obtener el producto de una fracción por un decimal?
En este caso ubica los 3/5 que es la cantidad de leche contenida en la jarra y los multiplicas por los 3.5 litros que son su capacidad máxima. A continuación, realiza dicha operación.
Coloca primero la fracción que, en este caso, son 3/5 y convertimos el número decimal a fracción decimal. Coloca como numerador las cifras 3 y 5, sin el punto decimal, es decir, 35, y como denominador escribe 10, porque 3.5 sólo tiene una cifra decimal. Después multiplicamos tres quintos por 35 décimos, cuyo resultado es igual a 105/50, que es la cantidad de leche que tiene la jarra. Finalmente, dividimos 105 entre 50 para convertir el resultado en número decimal. Sabemos que en términos de una división el numerador es el dividendo y el divisor el denominador, quedando de la siguiente manera:
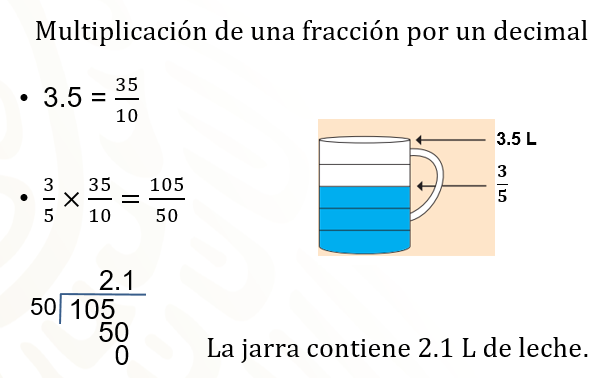
105 entre 50 es igual a 2.1. Entonces la cantidad de leche que contiene la jarra es de 2.1 litros.
Lo anterior lleva a reflexionar sobre la aplicación de las fracciones en distintos contextos.
Por ejemplo, la fracción de un bote de pintura para poder pintar una pared, o el cálculo de la fracción de consumo de gasolina de un trayecto de un lugar a otro, e incluso existen distintas formas de aplicar la multiplicación de fracciones para determinar ciertas situaciones que requieren su uso o aplicación. Por ejemplo…
“Abel ha observado que su automóvil gasta menos gasolina cuando existe mayor nivel de movilidad y menos tráfico vehicular, y para calcular el consumo de combustible se utiliza una tabla que el fabricante diseñó, la cual representa el comportamiento del consumo. Según el manual, el tanque de gasolina tiene capacidad de 48 litros, entonces para calcular cuántos litros de gasolina contiene el tanque cuando marca 1/2, 1/8, 1/12, etcétera, es necesario que te auxilies del tema visto durante esta lección.
Analiza la siguiente tabla:
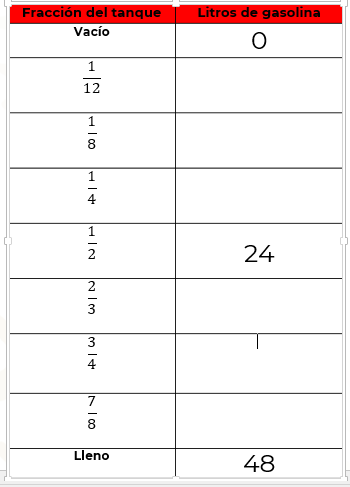
La tabla contiene dos columnas, en la columna izquierda, nombrada “Fracción del tanque”, se ubican las siguientes cantidades a modo de fracción: un doceavo, un octavo, un cuarto, un medio, dos tercios, tres cuartos y siete octavos; mientras que la columna de la derecha, llamada “Litros”, presenta la cantidad de litros en el tanque que le corresponden a cada fracción. El reto es encontrar los valores faltantes para saber cuántos litros de gasolina le corresponden a cada fracción.
Calcula las cantidades solicitadas y así ayudar al profesor Abel. Para encontrar esos valores debemos considerar que un número entero puede representarse como una fracción, en la que el numerador es el mismo número y el denominador es 1, esto se hace con el objeto de aplicar adecuadamente la multiplicación de fracciones:
A continuación, anotarás en la segunda columna la operación y el resultado correspondiente. Aplica el procedimiento que ya conoces para multiplicar fracciones: multiplicas numerador por numerador y denominador por denominador.
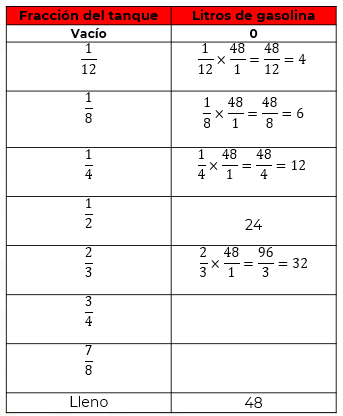
Comienza con 1/12, donde tienes que multiplicar numeradores 1 por 48 igual a 48 y los denominadores 12 por 1 igual a 12 y obtienes la fracción 48/12; después, procedemos a dividir 48 entre 12, donde el resultado es igual a 4 litros.
En el caso de 1/8, multiplicamos 1 por 48, y 8 por 1, resultando la fracción 48/8, al dividir 48 entre 8 el resultado es igual a 6 litros.
Aplica el mismo procedimiento en los siguientes casos: para 1/4, el resultado es 48/4 y al dividir 48 entre 4 el resultado es igual a 12 litros.
Para 2/3 por 48, el resultado es igual a 96/3, al dividir 96 entre 3 el resultado es igual a 32 litros.
Observa el siguiente ejemplo:
“En una escuela secundaria se va a pintar un muro de forma rectangular que mide 12 m de largo por 3 m de altura. Para los dos tercios de la parte superior del muro se empleará pintura de color beige y el tercio restante de la parte inferior se pintará de color marrón.”
Si, en general, el rendimiento de una pintura es de 1/10 de litro por metro cuadrado, ¿qué cantidad de pintura de cada color se requiere para pintar el muro?
Primero tienes que calcular el área del muro, multiplicando el largo por ancho. Ya que el muro tiene forma rectangular, en este caso se hace la operación:
12 metros por 3 metros y el resultado es igual a 36 metros cuadrados, que representan el área del muro.
Ahora calcula los metros cuadrados de cada color de pintura:
2/3, que corresponden a la parte superior del muro, por 36 metros cuadrados obtenidos previamente es igual a 72/3 de metro cuadrado. Luego divide 36 entre 3 y el resultado es igual a 24 metros cuadrados.
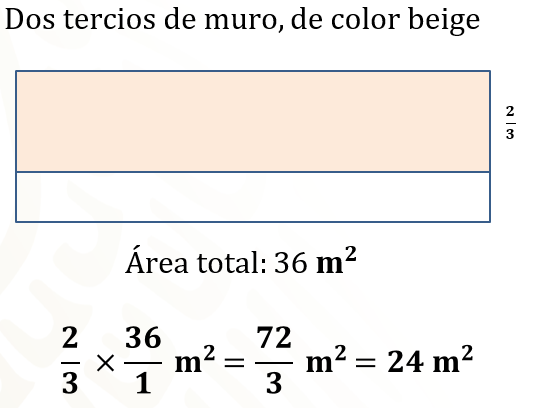
Esos 24 metros cuadrados corresponden a la parte superior,
Multiplica 24 por un décimo de litro, cuyo resultado es igual a 24 décimos de litro; al dividir el resultado anterior vemos que se necesitan 2.4 litros de pintura beige.

Ahora obtén la cantidad de pintura correspondiente a la parte inferior del muro:
Conocer la cantidad de pintura marrón que se usará es más sencillo, ya que la parte inferior, que corresponde a un tercio del muro, es la diferencia de 36 menos 24, que, a su vez, es el valor correspondiente a la pintura de la parte superior del muro, siendo su resultado: 12 metros cuadrados.

Dicho valor se multiplicará por un décimo, obteniendo 12 décimos, y al dividir 12 entre 10 tenemos 1.2 litros.
La multiplicación de fracciones es de gran ayuda en la resolución de situaciones que se ubican dentro de nuestra cotidianidad, pero: ¿en qué otras situaciones pueden emplearse este tipo de operaciones?
Observa la siguiente situación:
“Un tráiler se mueve manteniendo la misma velocidad durante cierto periodo en su recorrido a lo largo de una carretera, desplazándose a 80 kilómetros por hora. A continuación, se presenta una tabla en la que se ubica la fracción de tiempo, en horas y la distancia recorrida por el tráiler en kilómetros.”
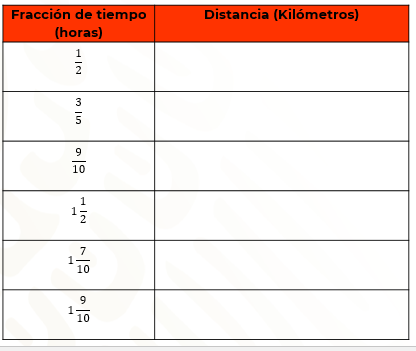
En la primera columna se ubican las fracciones de tiempo, 1/2, 3/5, 9/10, 1 entero 1/2, 1 entero 7/10 y 1 entero9/10, respectivamente.
Tienes que resolver una multiplicación de una fracción por un entero, para determinar la distancia correspondiente a cada caso. Como puedes ver, la tabla presenta fracciones propias y números mixtos, que son aquellos que implican la suma abreviada de un número entero y una fracción propia.
Ubica los valores dentro de la tabla para tener un mejor manejo de cada uno de ellos, no sin antes incluir en la segunda columna las operaciones junto con los resultados.
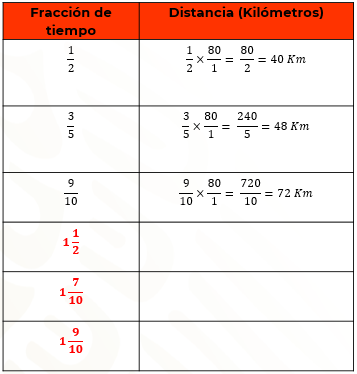
Multiplica 1/2 por ochenta, que es igual a 80/2, luego dividimos 80 entre 2, lo cual es igual a 40 kilómetros.
Después multiplica 3/5 por 80, que es igual a 240/5 y divide 240 entre cinco, cuyo resultado es igual a 48 kilómetros.
El siguiente valor en la tabla es 9/10, el producto de 9/10 por 80 es igual a 720/10, al dividir el resultado tenemos 72 kilómetros.
Se sabe que para multiplicar un número mixto por un entero, lo tenemos que hacer en dos pasos: primero convierte el número mixto a fracción impropia de la siguiente manera: multiplica la parte entera por el denominador y al resultado le sumas el numerador; el resultado es igual al numerador de la fracción impropia y se deja el mismo denominador.
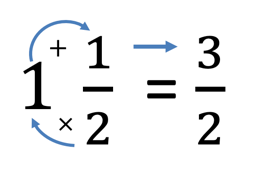
Ahora bien, 1 entero 1/2 lo conviertes a una fracción impropia obteniendo tres medios, que multiplicaras por 80 y obtenemos que 3/2 por 80 es igual a 240/2 de kilómetro que es igual a 120 kilómetros.
Continua con 1 entero 7/10, conviértelo a una fracción impropia; entonces multiplicamos 17/10 décimos por 80, que es igual a 1360/10, que al dividir es igual a 136 kilómetros.
Finalmente, con 1 entero 9/10, procedemos a convertirlo a una fracción impropia, cuyo resultado es 19/10 que multiplicarás por 80/1, el producto de 19 por 80 es 1520, sabiendo que el resultado del producto de los denominadores es 10 y al dividir obtienes que esto es igual a 152 kilómetros.
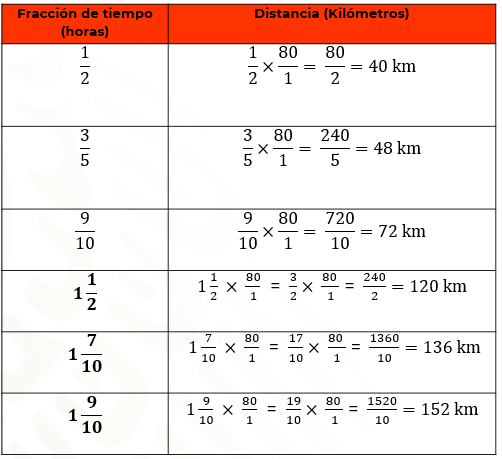
Se ha visto, a lo largo de esta sesión, la necesidad de utilizar el producto de fracciones para manipular adecuadamente los ingredientes de una receta de cocina, o la medida adecuada de la fracción correcta para pintar un muro, incluso el calcular el gasto de gasolina en un automóvil o la distancia recorrida por un tráiler en un intervalo de tiempo determinado.
El reto de hoy:
Observa la otra situación en la que se puede aplicar la multiplicación de fracciones.
“Hace unos días Abel compró una varilla de 3.5 metros de largo, de la cual utilicé tres cuartas partes para un arreglo de mantenimiento en mi hogar. Ahora necesita comprar otra varilla de la misma medida de la parte que utilizó.”
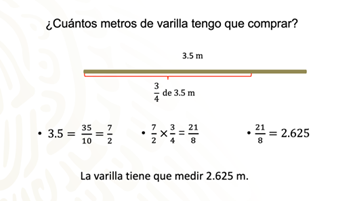
¿Cuántos metros de varilla tiene que comprar?
Para conocer la medida de la varilla que tiene que comprar, primero convierte 3.5 metros en fracción.
3.5 es igual a 35/10 y, al simplificar esta fracción, se obtienen 7/2.
Ahora multiplica 7/2 por 3/4. Al hacer el producto de los numeradores, tenemos que 7 por 3 es 21 y, haciendo lo pertinente con los denominadores, se tiene que 2 por 4 es 8, el resultado final es 21 octavos de metro.
Dividimos 21 entre 8 y obtenemos 2.625.
Por lo tanto, la varilla debe medir 2.625 metros.
Durante esta lección aprendiste que puedes resolver situaciones problemáticas en las que realizaste el producto de dos fracciones, o la multiplicación de un entero por una fracción, un decimal por fracción e incluso fracciones mixtas por enteros u otras fracciones propias e impropias.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
https://www.conaliteg.sep.gob.mx/