Medidas de tendencia central y rango
Medidas de tendencia central y rango
Aprendizaje esperado: consolidar los contenidos del eje Análisis de datos.
Énfasis: integrar los contenidos del tema Estadística.
¿Qué vamos a aprender?
En esta lección, harás un compendio o resumen sobre varios temas concernientes al análisis de datos. Comenzarás hablando sobre las medidas de tendencia central, que son de gran utilidad para representar conjuntos de datos. Continuarás estableciendo el procedimiento para construir gráficas circulares, que representan a estos conjuntos; lo que servirá para reconocer el uso del porcentaje para construirlas.
Para hablar sobre todas estas nociones y procedimientos observarás de un ejemplo extraído durante el presente ciclo escolar en una secundaria al norte del país.
¿Qué hacemos?
Un grupo de estudiantes de primer grado decidió comenzar un proyecto de fomento a la lectura. Impulsaron la creación de cuentos cortos para generar un catálogo virtual al que pudiera acceder toda la comunidad escolar. Subieron los cuentos a una plataforma que diseñaron las alumnas y alumnos de tecnología, con énfasis en Informática.
El proyecto fue todo un éxito, las alumnas y alumnos de primer grado produjeron 500 cuentos sobre diferentes temáticas. Así que, para realizar una valoración del impacto que tuvo su proyecto en la comunidad escolar, decidieron hacer un informe a los miembros del Consejo Técnico Escolar y al Consejo Escolar de Participación Social. En dicho informe darán a conocer la cantidad de estudiantes que participaron en la creación de, al menos, un cuento. Además, mostrarán la diversidad de temáticas de los cuentos y cuántos existen disponibles, de cada una de ellas, en su catálogo digital.
Con los datos recolectados en la plataforma, determinarás el promedio de las descargas diarias de los cuentos durante los primeros tres meses del proyecto. Esto servirá como indicador del impacto de su proyecto en la comunidad mostrarán la información sobre los rangos etarios que descargaron al menos un cuento durante el mismo periodo de tiempo.
Comienza aportando algunos datos del ejemplo. Participaron 315 estudiantes de entre 10 y 13 años.
De 10 años participaron: 2 estudiantes
De 11 años participaron: 196 estudiantes
De 12 años participaron: 114 estudiantes
De 13 años participaron: 3 estudiantes
¿Qué medidas de tendencia central existen que pueden ayudar a encontrar un valor que sea representativo de la edad de los participantes? Escribe en tu cuaderno la respuesta.
Como has visto antes, las medidas de tendencia central ayudan a encontrar un valor representativo de un conjunto de datos. Las medidas más utilizadas son: La media aritmética o promedio; la moda y la mediana.
La media aritmética o promedio, se calcula sumando el valor de todos los datos de un conjunto y luego dividiendo el resultado entre el número de datos contenidos en él. Como probablemente sabes, se usa mucho esta medida de tendencia central en la escuela. Por ejemplo, cuando se busca representar con un solo valor numérico a todos los datos de evaluación obtenidos en un periodo escolar, mejor conocido como promedio.
Para que la elección de la medida de tendencia central sea apropiada, aunado a las medidas de tendencia central, es necesario considerar una medida de dispersión.
Para saber qué tan adecuada es la medida de tendencia central se usan las medidas de dispersión que son números que indican si un dato se separa mucho, poco, o nada, con respecto a otro. Las medidas de dispersión son: el rango, la varianza, la desviación típica y el coeficiente de variación.
La medida de dispersión que se analizará por ahora es el rango, el cual se obtiene restando el dato mayor, menos el dato menor del conjunto. Esta diferencia permite conocer qué tan alejado está el dato mayor del dato menor. Cuando están muy alejados el uno del otro; es decir, cuando el valor del rango es grande, entonces el valor de la media aritmética o promedio también estará lejos de representar apropiadamente a todo el conjunto.
Dado que las medidas de tendencia se encargan de resumir información de un conjunto de datos numéricos, la medida que elijamos no debe estar alterada por valores atípicos o por un rango amplio. Cuando esto sucede, no es conveniente usar a la media aritmética o promedio; de hecho, el conjunto quedará mejor representado por la mediana o la moda que son menos susceptibles a valores atípicos o a un rango amplio.
La moda es el número con mayor frecuencia en el conjunto; es decir, el dato que más se repite.
La mediana, está en medio del conjunto de datos, pero estos deben estar ordenados, ya sea de menor a mayor o de mayor a menor.
¿Qué medida de tendencia central será la ideal para representar la edad de las y los estudiantes que crearon cuentos?
Es posible observar en los datos, que existen valores atípicos. De los 315 estudiantes que participaron, sólo 2 y 3 tienen 10 y 13 años de edad respectivamente; así que, para este ejemplo, usar la media aritmética no es útil.
Si restas 13 años menos 10 años se obtiene el rango de edad que, en este caso, vale 3. Aunque este rango no es demasiado amplio, basta con la presencia de valores atípicos para decidir no usar a la media aritmética o promedio para representar este conjunto.
¿Qué medida es mejor utilizar?
La medida más conveniente para utilizar es la mediana, ya que no se ve alterada por valores atípicos extremos. Para calcularla, es necesario ordenar todos los valores. Se deben ordenar los 315 valores de edad de mayor a menor o de menor a mayor.
Enseguida, se ubica el número central.
Para un conjunto con un número impar de datos, existe un valor central único, de manera que este valor representa la mediana del conjunto. Sin embargo, para un conjunto par, existen dos valores centrales. El valor de la mediana es la media o promedio de estos dos valores; es decir, el resultado de sumar ambos valores centrales y luego dividirlos entre dos.
Para el ejemplo, al ordenar el conjunto de menor a mayor se obtiene que el valor central es 11.
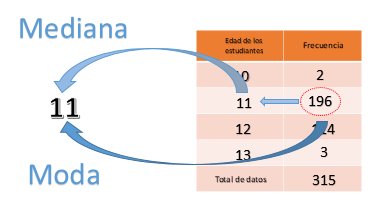
Como son 315 datos, es posible saber que el valor central estará en la posición 158. En el conjunto se tienen 2 datos con valor 10 y 196 datos con valor 11; por lo que es evidente observar que, en la posición 158, se encontrará un dato con valor 11.
Claro que la moda también puede ser de utilidad. Como la moda es el valor que más se repite en el conjunto, es posible observar que 11 también es la moda de este conjunto, ya que este valor se repite 196 veces.
Cabe señalar que en un conjunto de datos puede haber más de una moda; es decir, que haya coincidencia en el número de repeticiones para uno o más datos. A ese tipo de conjuntos se les llama multimodales.
En segunda instancia, el grupo de estudiantes que rendirán el informe, quieren dar a conocer las temáticas de los cuentos que se ofrecieron en el catálogo virtual. Se clasificaron 500 cuentos en 5 temáticas: Acción y aventuras, Ciencia Ficción, Infantiles, Romance y Terror. Observa los siguientes datos:
Acción y aventuras: 150 cuentos
Ciencia ficción: 100 cuentos
Infantiles: 40 cuentos
Romance: 130 cuentos.
Terror: 80 cuentos.
Lo más pertinente, al rendir un informe, es representar la información mediante un gráfico. Hazlo utilizando una gráfica circular, también llamada gráfica de sectores o gráfica de pastel, la cual tiene como objetivo representar variables cualitativas o categóricas. Se utiliza para mostrar las proporciones por medio de porcentajes. Consta de un círculo dividido en sectores que corresponden a categorías de datos. El tamaño de cada sector es proporcional a la frecuencia de la categoría que representa. Es importante mencionar que la unidad de medida de un sector circular son los grados y un círculo comprende 360 grados.

Organiza los datos en una tabla. En la primera columna, colocarás las temáticas: acción y aventuras, ciencia ficción, infantiles, romance y terror; en la segunda columna el número de cuentos: 150, 100, 40, 130 y 80; que al sumarlos resulta un total de 500. Agrega tres columnas más: frecuencia relativa, porcentaje y ángulo del sector circular.
La frecuencia relativa es el cociente entre la frecuencia absoluta de un determinado valor y el número total de datos. En este caso, las frecuencias absolutas son el número de cuentos por temática y el total de datos es 500.
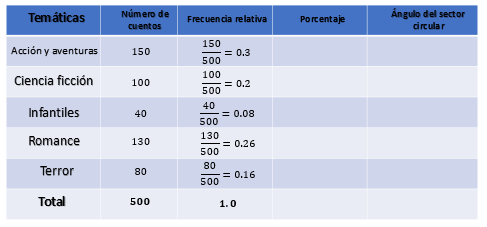
Para calcular las frecuencias relativas, se debe dividir el número de cuentos por temática, entre el total de cuentos. Para acción y aventuras, divide 150 entre 500, obtienes tres décimos; ciencia ficción divides 100 entre 500, igual a dos décimos; infantiles, divide 40 entre 500, igual a ocho centésimos; romance, dividimos 130 entre 500, igual a veintiséis centésimos; y para terror, divides 80 entre 500, igual a dieciséis centésimos. Al sumar las frecuencias relativas se obtiene un entero.
Ahora, calcula los valores de la columna de porcentaje. Por ciento significa “por cada cien” y se refiere a la razón entre una cantidad dada y un total de 100 elementos; así que “tanto por ciento” significa una cantidad por cada cien. Se usa el símbolo % para representar un porcentaje.
Cabe destacar que la razón asociada con el tanto por ciento se puede representar mediante una fracción con denominador 100, lo que la convierte en una fracción decimal. Así que, para completar la columna de porcentaje en la tabla, utilizarás fracciones equivalentes a las que representan la relación entre el número de cuentos y el total de cuentos producidos. Estas fracciones serán decimales, ya que ahora usarás fracciones con denominador 100.
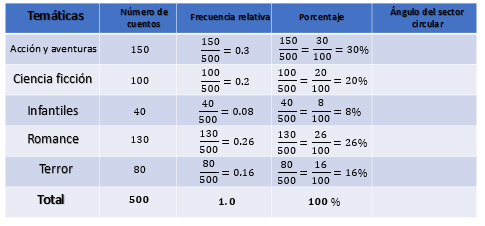
Como las fracciones que representan la relación de número de cuentos entre el total, tienen denominador 500 y se requiere que sea 100, debes dividir entre 5; por lo tanto, a los numeradores también los dividirás entre 5. Para acción y aventuras: 150/500 es equivalente a 30/100 que es igual a 30%; ciencia ficción: 100/500 es equivalente a 20/100 que es igual a 20%; infantiles: 40/500 es equivalente a 8/100 igual a 8%; romance: 130/500 es equivalente a 26/100 igual a 26% y para terror: 80/500 es equivalente a 16/100 igual a 16%. Al sumar los porcentajes se obtiene 100%.
Ahora que conoces la frecuencia relativa y el porcentaje, sólo resta calcular el ángulo del sector circular. La proporción que representa cada categoría respecto al total debe guardar la misma proporción que el sector circular que le corresponde respecto al círculo completo. Por consiguiente, al total de datos le corresponde el área que abarcan los 360º. Por lo tanto, el ángulo que corresponde a cada categoría debe cumplir con la proporción.
Categoría entre total igual a sector circular, entre 360º
Así que el ángulo para cada categoría está dado por:
Sector circular, igual a categoría, entre total, por 360º
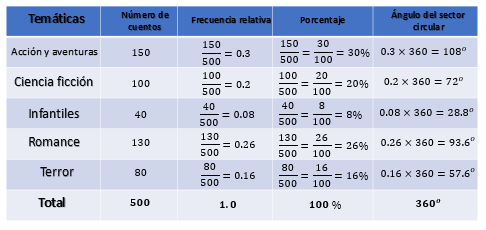
Para calcular la medida del ángulo del sector circular, debes dividir el valor de cada temática entre el total de cuentos y multiplicar por 360 grados. El valor de la categoría o temática entre el total de cuentos es lo que ya se calculó en la columna frecuencia relativa; así que sólo debes multiplicar dicha cantidad por 360. Para acción y aventuras: tres décimos por 360 igual a 108º; ciencia ficción: dos décimos por 360, igual a 72º; infantiles: ocho centésimos por 360, igual a 28. 8º; romance: veintiséis centésimos por 360, igual a 93. 6º; y terror: dieciséis centésimos por 360, igual a 57.6º. Al sumar las medidas de los ángulos se obtienen 360º, lo que comprueba que los cálculos son correctos.
Ya tienes todos los datos, sólo falta realizar la gráfica. Primero, debes trazar una circunferencia. La medida es indistinta y depende del área en la que se desee trazar la gráfica, puede ser en una hoja de papel o en un pliego completo. Enseguida, ubica el centro del círculo y traza un radio desde ese punto hasta cualquier otro punto de la circunferencia, generalmente se inicia de esta forma para seguir el sentido de las manecillas del reloj. Con el transportador, marca el primer ángulo que es de 108º. Coloca el transportador en el centro del círculo, pero ahora te apoyas en la marca anterior y ubicas la medida del segundo ángulo, que es de 72º. Vuelve a colocar el transportador en el centro, te apoyas en la marca anterior y mides el tercer ángulo que es de 28.8º. Nuevamente ubicas el transportador en el centro del círculo y marcas el cuarto ángulo, cuya medida es de 93.6º y, si los trazos fueron correctos, es posible comprobar que el último sector circular medirá un ángulo de 57.6º
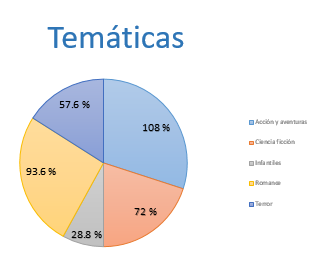
Ya tienes en la gráfica cada sector representado y etiquetado con el porcentaje que le corresponde: Acción y aventuras 108%, Ciencia ficción 72%, Infantiles 28.8%, Romance 93.6% y Terror 57.6%. A un lado del gráfico, aparece el nombre de las categorías con el color asociado a cada una de ellas.
Para medir el impacto que tuvo su proyecto en la comunidad el equipo analizó los datos que recolectó la plataforma durante los primeros tres meses del proyecto. ¿Cómo puedes conocer el promedio de descarga diaria de los cuentos disponibles en la plataforma?
Para conocer el promedio de descargas diarias se necesitan al menos dos datos: Primero hay que determinar el periodo de tiempo que se va a analizar. Enseguida, se requiere conocer el número de descargas en ese periodo de tiempo.
Tienes esos datos disponibles el periodo de tiempo abarca los meses de septiembre a noviembre, lo que significa un total de 91 días naturales. También es conocido que durante ese periodo se registraron 76 440 descargas. ¿Qué operaciones matemáticas se deben realizar?
Para conocer el promedio de descargas diarias simplemente se divide el número total de descargas en el periodo entre el número de días naturales, no de los meses sino de los días, porque se busca un promedio diario. De manera que 76 440 entre 91 resulta 840. Esto significa que en promedio diario se descargaron 840 veces los cuentos disponibles en la plataforma.
Es un excelente indicador del impacto del proyecto en la comunidad. Probablemente si suben más cuentos y continúan con el proyecto habrá más descargas y por consiguiente existirán más personas lectoras gracias a este proyecto escolar. Por otro lado, también es posible estratificar los datos que recolectó la plataforma. Estratificar significa agrupar según una característica de interés.
Al equipo le interesó estratificar las descargas según la edad del usuario que se registraron en el mismo periodo de tiempo, así que crearon 4 estratos o categorías:
La primera, descargas por personas menores de 18 años.
La segunda, descargas por personas de 18 y hasta los 30 años.
La tercera, descargas por personas mayores de 30 y menores de 60 años.
La cuarta, descargas por personas de 60 años o más.
En la imagen se puede observar la gráfica circular que construyeron a partir de esa información. En cada sector de la gráfica circular se encuentra el porcentaje asociado a la categoría correspondiente.

Para la primera categoría, descargas por personas menores de 18 años, se registró un 45 % del total de las descargas del periodo analizado.
Para la segunda, descargas por personas de 18 y hasta los 30 años, se registró un 25 % del total de las descargas del periodo analizado.
Para la tercera, descargas por personas mayores de 30 y menores de 60 años, se registró un 20% del total de las descargas del periodo analizado.
Finalmente, para la cuarta, descargas por personas de 60 años o más, se registró un 10% del total de las descargas del periodo analizado.
Es posible observar que la suma del porcentaje de los cuatro estratos o categorías es el 100% ¿Cómo puedes determinar el número de descargas por estrato?
El reto de hoy:
Determina el número de descargas por estrato

Para determinar el número de descargas por estrato o categoría es necesario conocer la frecuencia de cada estrato. La frecuencia es proporcional al porcentaje, así que para encontrar cada frecuencia determina la razón del porcentaje de cada estrato y el porcentaje total, que está dada por la fracción porcentaje de cada estrato sobre 100%.
Enseguida el cociente de la razón se multiplica por el número de descargas totales en el periodo para obtener número de descargas de ese estrato o categoría.
Calcula:
Para la primera categoría, descargas por personas menores de 18 años, se obtiene la razón 45% sobre 100%, lo que resulta 0.45 que al multiplicarlo por 76 440 que es el total de descargas del periodo analizado, se obtiene 34 398. Esto significa que 34 398 descargas provienen de usuarios menores de 18 años.
Para la segunda categoría, descargas por personas de 18 y hasta los 30 años, se obtiene la razón 25% sobre 100% lo que resulta 0.25 que al multiplicarlo por 76 440 se obtiene 19 110 Esto significa que 19 110 descargas provienen de usuarios de 18 y hasta los 30 años.
Para el tercer estrato, descargas por personas mayores de 30 y menores de 60 años, se obtiene la razón 20% sobre 100% lo que resulta 0.2 que al multiplicarlo por 76 440 se obtiene 15 288 Esto significa que 15 288 descargas provienen de usuarios mayores de 30 y menores de 60 años.
Finalmente, para la cuarta, descargas por personas de 60 años o más, se obtiene la razón 10% sobre 100% lo que resulta 0.1 que al multiplicarlo por 76 440 se obtiene 7 644 Esto significa que 7 644 descargas provienen de usuarios de 60 años o más.
Es evidente que la mayor cantidad de las descargas las realizaron personas menores de 18 años. Sin embargo, el alcance del proyecto tuvo un impacto igual en la población mayor de 18 y menor de 60 años. Ya que si sumas el porcentaje o la frecuencia de los estratos: personas mayores de 18 y hasta los 30 años más las personas mayores de 30 pero menores de 60 años también se tiene el 45%, o bien, 34 398 descargas en el periodo de septiembre a noviembre.
¡Hasta el próximo ciclo escolar!
Estimada y Estimado Estudiante:
Con esta clase se concluye el ciclo escolar 2022-2023. Fue un año de muchos aprendizajes, tu ánimo te impulsó para seguir adelante, hasta llegar a esta última clase del ciclo escolar.
Recuerda que puedes repasar tus clases, ya sea a través de los apuntes como éste, en el portal de Aprende en casa:
https://aprendeencasa.sep.gob.mx/site/index
Estamos muy orgullosos de tu esmero y dedicación. Quisiéramos que compartieras con nosotros tus experiencias, pensamientos, comentarios, dudas e inquietudes a través del correo electrónico:
aprende_en_casa@nube.sep.gob.mx
¡Muchas felicidades!
Hiciste un buen trabajo
* Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas