Medida de tendencia central más representativa de un conjunto de datos
Medida de tendencia central más representativa de un conjunto de datos
Aprendizaje esperado: usa e interpreta las medidas de tendencia central (moda, media aritmética y mediana) y el rango en un conjunto de datos y decide cuál conviene más en el análisis de los datos en cuestión.
Énfasis: calcular las medidas de tendencia central y del rango para establecer la medida más representativa del conjunto de datos.
¿Qué vamos a aprender?
Estudiarás el aprendizaje esperado: “usa e interpreta las medidas de tendencia central (moda, media aritmética y mediana) y el rango en un conjunto de datos y decide cuál de ellas conviene más en el análisis de los datos en cuestión”.
Calcularás las medidas de tendencia central y del rango para establecer la medida más representativa del conjunto de datos.
Los materiales que vas a utilizar en esta sesión son:
- Cuaderno o papel para tomar notas
- Lápiz, goma y sacapuntas
¿Qué hacemos?
El Instituto Nacional de Estadística y Geografía (INEGI) es un organismo público y autónomo que se responsabiliza de normar y coordinar el Sistema Nacional de Información, Estadística y Geografía, así como de registrar, clasificar y difundir la información de México conforme al territorio, los recursos, la población y la economía. Así, da a conocer las características de nuestro país para que los datos sean de ayuda en la toma de decisiones que procuren el bienestar social, político, comercial y sustentable de nuestro país.
Por ejemplo, gracias a los datos que informa el INEGI, cuando una institución de salud emprende una campaña de vacunación para todas las niñas y los niños menores de diez años de nuestro país, dicha institución sabrá cuántas son las vacunas que requiere llevar a cada región. De esta manera, los recursos se distribuyen correctamente para que las vacunas sean aplicadas de manera eficaz.
El INEGI ha representado una de las mayores fuentes de información y conocimiento en México, no sólo para instituciones y gobierno, sino para la población en general, pues, a través de sus estadísticas, es posible conocer un sinnúmero de datos sobre nuestro país y su población. Para ello, usa cálculos matemáticos para organizar, y analizar la información que presenta a la sociedad a través de estudios, reportes e informes.
Estos estudios se encuentran abiertos tanto al público en general como a la comunidad académica para emplearlos en sus trabajos y análisis de temas de interés.
Observa el siguiente ejemplo:
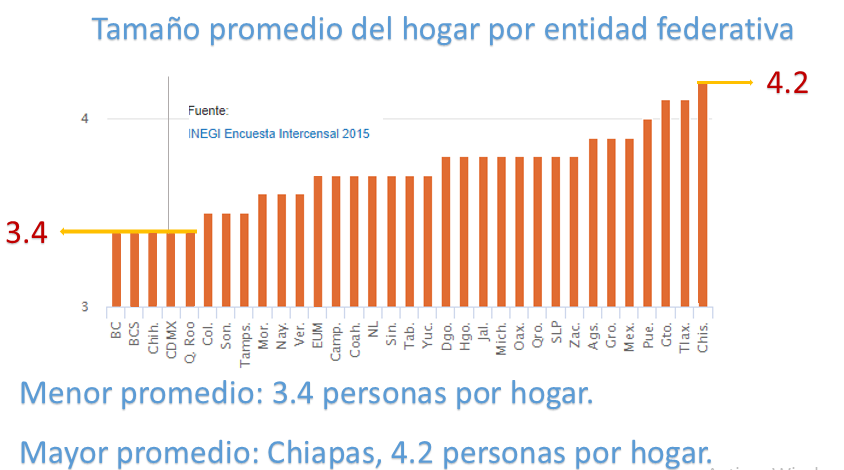
En la gráfica “Tamaño promedio del hogar por entidad federativa” es posible observar el número de personas que, en promedio, integran un hogar para cada uno de los estados de la República Mexicana. En la gráfica la información se encuentra ordenada de menor a mayor número de personas por hogar. Trata de ubicar tu estado para que identifiques el número de personas que les corresponde.
Como se observa en la gráfica, hay cinco estados en la República con el menor promedio: 3.4 personas por hogar, y son Baja California, Baja California Sur, Chihuahua, Ciudad de México y Quintana Roo; el estado con mayor promedio es Chiapas con 4.2 personas, mientras que el promedio del país es de 3.7 personas por hogar.
Se sabe que no es posible que en un hogar existan 3.4 o 4.2 personas, pero en cuestiones estadísticas, ¿qué significa que vivan, en promedio, 3.7 personas en cada hogar mexicano?
¿Cuántas personas viven en tu casa?, ¿Coincide el número de personas que viven en tu casa con el promedio de tu estado o con el promedio nacional?, ¿Qué tanto se acerca?
Para profundizar en tu respuesta a estas interrogantes es importante considerar que, para analizar un conjunto de datos, es posible hacer uso de diversas medidas de tendencia central; o bien, de medidas de dispersión. En este ejemplo sólo aparece una de ellas: la media aritmética o promedio. Presta atención para identificar qué otras medidas de tendencia central existen.
Observa el siguiente video a partir del minuto 00:30 a 00:54.
- Propiedades de las medidas de tendencia central
https://youtu.be/gKE-pNOomgg
Observa el siguiente video a partir del minuto 00:39 a 01:04. - Relación entre el rango y la posible dispersión de los datos
Como se observa, las medidas de tendencia se encargan de resumir información de un conjunto de datos numéricos. De manera que el conjunto queda representado por la moda, la mediana o la media aritmética.
- La moda es el número con mayor frecuencia, es decir, el dato que más se repite.
- La mediana es el centro de los datos desde el punto de vista numérico, es decir, está en medio del conjunto de valores cuando éstos están ordenados, ya sea de menor a mayor o de mayor a menor.
- La media aritmética o promedio se calcula sumando todos los datos del conjunto y dividiendo entre el número total de datos.
Por otra parte, las medidas de dispersión nos informan sobre cuánto se alejan del centro los valores de la distribución. Por ahora, sólo estudiarás una de ellas, el rango.
El rango es la diferencia entre el dato mayor y el menor de un conjunto de valores. Esta medida de dispersión permite conocer qué tan alejados se encuentran los valores de un conjunto de datos entre sí.
Consideramos un ejemplo para analizar las medidas mencionadas. Una pequeña empresa tiene 7 empleados, de quienes se conoce su salario mensual. En una tabla se han registrado los salarios de cada empleado. A partir de las medidas de tendencia central: moda, mediana y media aritmética, hay que determinar cuál es el sueldo más representativo del conjunto de datos.
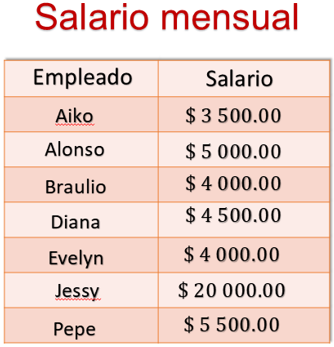
En la tabla se encuentra el nombre de los empleados y el salario mensual de cada uno, se observa que: Aiko gana 3 500 pesos, Alonso 5 000 pesos, Braulio 4 000 pesos, Diana 4 500 pesos, Evelyn 4 000 pesos, Jessy 20 000 pesos y Pepe 5 500 pesos.
¿Cuál es la media del conjunto de datos? ¿Qué tienes que hacer para obtenerla? ¿Cuál es la moda? ¿Cuál es la mediana?
Primero, encuentra el valor de la moda que, como se mencionó antes, es el dato que más se repite.
Observa nuevamente la tabla de datos para calcular este valor.

Es necesario revisar con cuidado los salarios para saber cuál es el que más se repite: 3 500 pesos, 5 000 pesos, 4 000 pesos, 4 500 pesos, 4 000 pesos, 20 000 pesos y 5 500 pesos. Puedes notar que 4 000 pesos es el dato que más se repite, ya que aparece dos veces.
Por lo tanto, la moda del conjunto es 4 000 pesos.
¿Consideras que este valor puede ser representativo del salario de los empleados de la empresa? Toma nota de tus conjeturas, más adelante las analizarás.
Ahora realiza el cálculo de la mediana. Para ello, los datos deben estar ordenados de menor a mayor o de mayor a menor. En este caso los ordena de menor a mayor, pero tú puedes hacerlo de mayor a menor y observar que coincida en el cálculo.
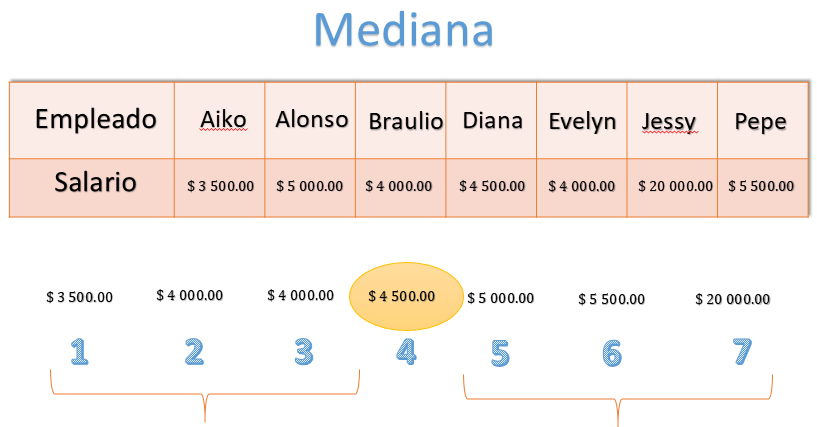
El ordenamiento resulta: 3 500 pesos, 4 000 pesos, 4 000 pesos, 4 500 pesos, 5 000 pesos, 5 500 pesos y 20 000 pesos. Cuenten ahora los datos, uno, dos, tres, cuatro, cinco, seis y siete, el dato que se encuentra a la mitad es 4 500; por lo tanto, la mediana es 4 500 pesos.
¿Este valor podría representar adecuadamente el salario de los empleados?
Para el cálculo de la media aritmética o promedio es necesario sumar todos los datos y dividir el resultado entre el total de ellos, que en este caso son siete.
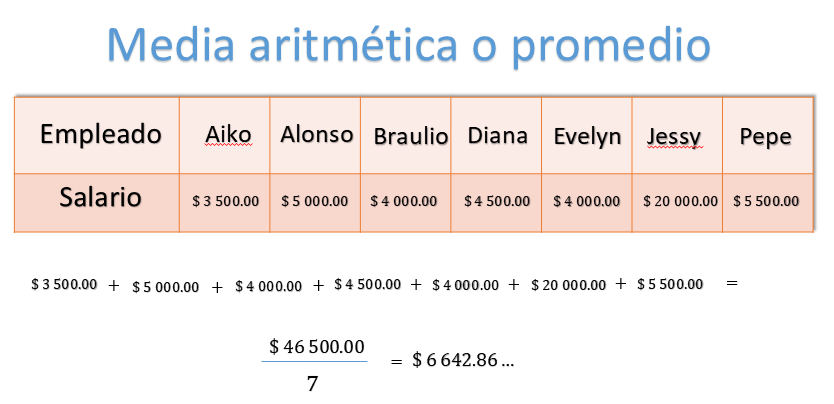
Así, 3 500 pesos, más 5 000 pesos, más 4 000 pesos, más 4 500 pesos, más 4 000 pesos, más 20 000 pesos más 5 500 pesos igual a cuarenta y seis mil quinientos pesos.
Al dividir esta cantidad entre 7 resultan 6 624.86 pesos, redondeado a centésimos. Por lo tanto, la media aritmética o promedio es: 6 624.86 pesos.
Compara a la media con los salarios. ¿Consideras que este valor podría ser un dato representativo de los salarios?
Ya tienes las tres medidas de tendencia central:
La moda es igual a 4 000 pesos, la mediana es igual a 4 500 pesos, y la media aritmética o promedio es igual a 6 624.86 pesos.
¿Cuál medida consideras que representa mejor al conjunto de datos?
Es notable que los tres datos son muy distantes entre sí y sería complicado tomar una decisión certera, para ello se recurre al cálculo del rango.
Calcula el rango de los sueldos. La existencia de un rango alto significa que los datos son numéricamente muy distintos entre sí; en cambio un rango bajo indica que los datos son muy parecidos entre sí. Para calcular el rango obtienes la diferencia entre el dato mayor y el dato menor. El dato mayor, en este caso, es 20 000 pesos, menos el dato menor, que es 3 500 pesos, el rango será de 16 500 pesos en este conjunto de datos.

El rango, al ser un intervalo entre el valor máximo y mínimo de un conjunto de datos, te permite obtener una idea de la dispersión de los mismos; cuanto mayor es el rango, más dispersos están los datos. En este caso, el rango resultó ser 16 500 pesos, esto indica que los datos extremos son muy distantes entre sí.
Esta información es de utilidad para afirmar que la mediana es la medida que mejor representa a este conjunto de datos. Además, reflexiona que no podría ser la moda, ya que menos del 50 % de las personas ganan 4 000 pesos y tampoco es factible considerar a la media aritmética, ya que está por arriba de la mayoría de los salarios y sólo una persona gana más de 6 624.86 pesos.
Se dice que la distribución de un conjunto de datos es simétrica respecto a la media cuando ésta coincide aproximadamente con la mediana, es decir, cuando se encuentra muy cerca del centro del conjunto de datos. Los valores atípicos, que son muy distantes de la mayoría de los valores, pueden afectar considerablemente el análisis de los resultados, como fue el caso de los salarios, en donde 20 000 pesos se considera como un dato atípico del conjunto, por estar muy alejado de la mayoría de los salarios.
En estos casos el conjunto de datos se considera asimétrico respecto a la media.
Con base en lo que has aprendido hasta ahora, es posible que, ya puedas calcular las medidas de tendencia central y el rango para determinar cuál es la medida que representa mejor al conjunto de datos de la siguiente situación. Presta atención del minuto 01:45 a 01:53.
- Relación entre el rango y la posible dispersión de los datos
Algunas veces, la información que se va a analizar o procesar está contenida en gráficas. Tal es el caso de la situación planteada. Esto no es un impedimento para realizar los cálculos necesarios y, así, determinar cuál medida los representa mejor.

Comienza con la moda. Para obtenerla observa si hay barras que se repiten. Si así es el caso, ¿cuál es el valor asociado a las barras que se repiten más? En este caso, hay cuatro barras que se repiten y están asociadas al número 8. Por lo tanto, la moda es: 8 focos.
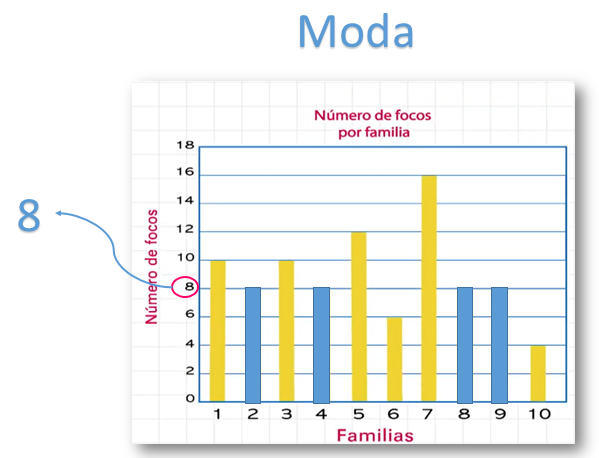
Para calcular la mediana es necesario ordenar los datos de mayor a menor o de menor a mayor; esta vez los ordenarás en forma descendente, es decir, de mayor a menor, quedando: 16, 12, 10,10, 8, 8, 8, 8, 6 y 4.
El conjunto de datos está formado por 10 elementos. Noten que, al centro, quedan dos datos.
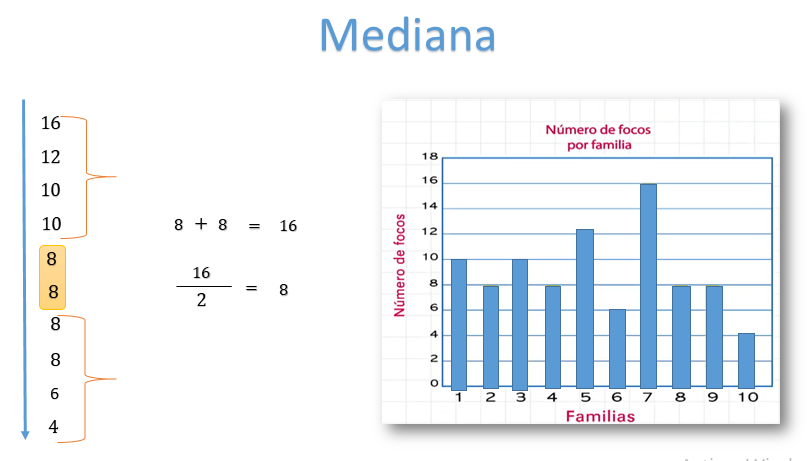
Cuando esto sucede, es necesario calcular la media aritmética de dichos números.
Así, la mediana resulta el valor central de todo el conjunto.
Para este caso, la media aritmética se calcula sumando 8 más 8, que es igual a 16. Enseguida, se divide entre dos, lo que resulta 8.
Por lo tanto, la mediana de este conjunto de datos es 8.
Ahora, calcula la media aritmética o promedio. Para ello se procede a sumar todos los datos, es decir 10 + 8 + 10 + 8 + 12 + 6 + 16 + 8 + 8 + 4, que es igual a 90.
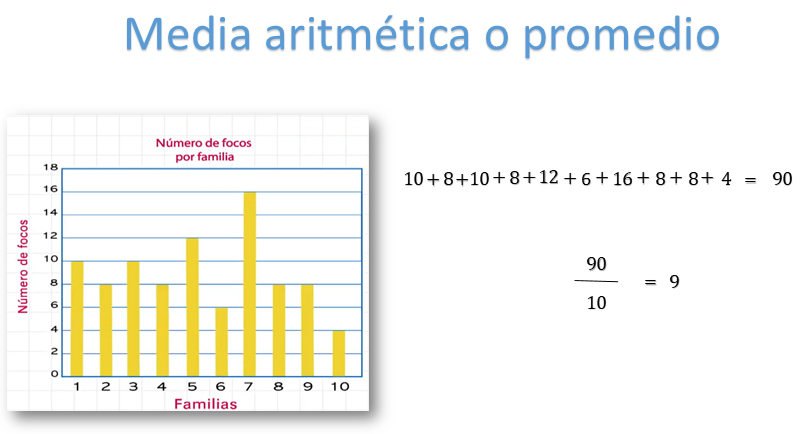
Después, se divide 90 entre 10, ya que son 10 datos en total; así 90 entre 10 es igual a nueve. Por lo tanto, la media aritmética del conjunto de datos es 9.
Se sabe, entonces, que para los datos representados en la gráfica las medidas de tendencia central son:
La moda es igual a 8 focos, la mediana es igual a 8 focos y la media aritmética o promedio es igual a 9 focos.
¿Qué medida es más representativa del número de focos que hay por familia?
Es posible notar que los valores de la moda y la mediana son iguales. Además, aunque el valor de la media aritmética es distinto, es muy parecido. Para tomar una decisión más certera sobre cuál medida representa mejor al conjunto, calculemos el rango.

Para calcular el rango debes tomar el dato mayor, que es 16 y restarle el dato menor, que en este caso es 4; esto es igual a 12.
Por lo tanto, el rango es 12.
Como puedes observar, en este caso, la mejor medida para representar los datos contenidos en la gráfica es la mediana, debido, precisamente, a que el rango es muy amplio, considerando los valores del conjunto. Lo que significa que los datos son muy dispersos.
Ahora, retoma el ejemplo inicial, organiza en una tabla de frecuencias los datos que pudiste observar en la gráfica. La frecuencia es el número de veces que se repite un dato del conjunto.
En la tabla colocas en la primera columna el número de personas promedio que viven en el hogar, que son: 3.4, 3.5, 3.6, 3.7, 3.8, 3.9, 4.0, 4.1 y 4.2.
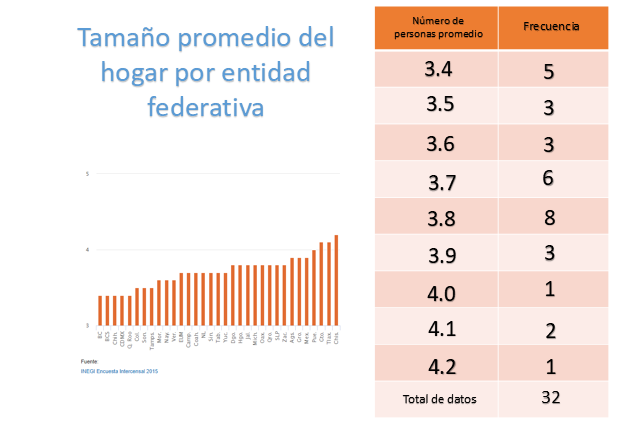
En la segunda columna colocamos la frecuencia, es decir, el número de entidades que registraron cada dato: 5, 3, 3, 7, 8, 3, 1, 2, y 1. En la última fila escribimos la suma total de datos que en este caso son 32, que corresponde al total de estados de la República Mexicana.
La media aritmética de este conjunto ya la conocemos y es de 3.7 personas. Ahora, calculemos las medidas faltantes.
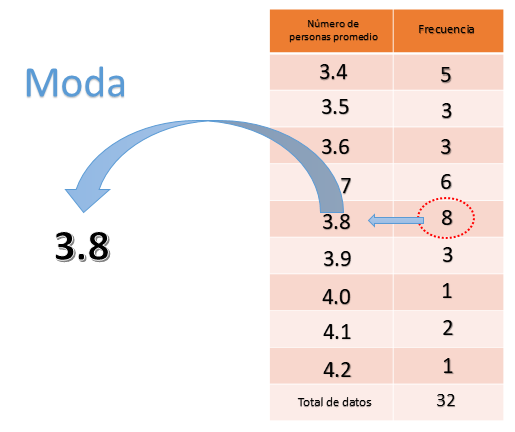
Comienza con la moda, que es el dato que tiene mayor frecuencia. En este ejemplo las frecuencias son, 5, 3, 3, 6, 8, 3, 1, 2, 1. La frecuencia mayor es 8. El número de personas asociado a la frecuencia 8 es 3.8; por lo tanto, 3.8 es la moda de este conjunto de datos.
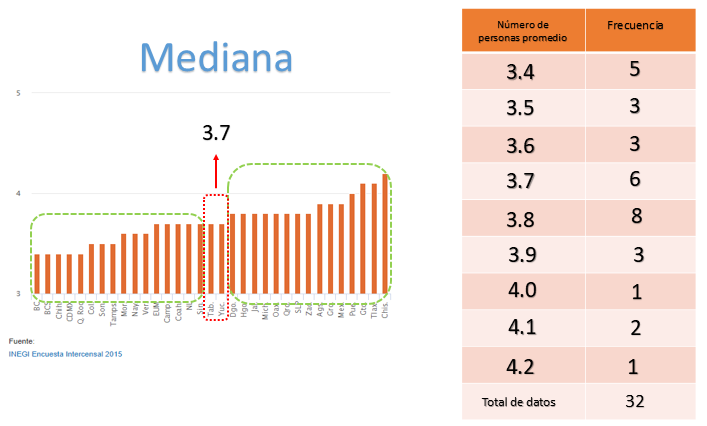
Calcula ahora la mediana. Para ello, hay que ordenar los datos de mayor a menor o de menor a mayor. Para facilitar el cálculo, el uso de la gráfica de la cual tomas los datos es la mejor opción, ya que se encuentra en orden ascendente. Al ser 32 datos, quedan quince de un lado, quince del otro y al centro podemos observar dos datos, que son el mismo valor. Por lo tanto, la mediana del conjunto es de 3.7.

Finalmente, calcula el rango. Al valor del dato mayor, que es 4.2, le restamos el valor del dato menor, que es 3.4; esto es igual a 0.8. Por lo tanto, el rango es 0.8. En este caso, puedes observar que este valor es un número relativamente pequeño, en comparación con los valores del conjunto de datos, lo cual quiere decir que los datos del conjunto de números son muy cercanos entre sí, lo que significa que la dispersión es muy poca.
Ya tenemos las tres medidas de tendencia central:
Moda es igual a 3.8 habitantes por hogar, mediana es igual a 3.7 habitantes por hogar y la media aritmética o promedio es igual a 3.7 habitantes por hogar.
La media y la mediana están representadas por el mismo número y la moda es una décima más que las dos anteriores, con lo cual compruebas que las tres medidas están representadas por datos muy cercanos, tal como lo interpretamos al calcular el rango.
Por lo tanto, es posible concluir que la medida de tendencia central que mejor representa al conjunto de datos es la media aritmética.
El reto de hoy:
Si ya tienes tu libro de Matemáticas de primer grado, ubica en él este tema. Resuelve todo lo que puedas para practicar; puedes encontrar los libros de texto en la página de la Secretaría de Educación Pública.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas