Leonardo de Pisa y las matemáticas de la vida

Leonardo de Pisa y las matemáticas de la vida

Aprendizaje esperado: concibe las matemáticas como una construcción social en la que se formulan y argumentan hechos y procedimientos matemáticos.

Énfasis: reconocer las aportaciones de Fibonacci a las matemáticas.

¿Qué vamos a aprender?

Las matemáticas tienen su propia historia y, por supuesto, tienen sus personajes famosos e importantes. Uno de ellos es Leonardo de Pisa. Este renombrado matemático dio a conocer una importante sucesión de números que llevan su nombre y en esta sesión conocerás sobre él y sus aportaciones.

¿Qué hacemos?

Para comenzar, hay que ubicarse histórica y geográficamente.

Es aproximadamente el año 1,140, en Pisa, Italia. Esta época es conocida como la Edad Media, un periodo de la historia que duró 10 siglos, lo que es igual a ¡Mil años!

En esa época, la mayoría de los europeos usaban los números romanos; estos consisten en siete letras, que seguramente conoces: I, V, X, L, C, D y M, que corresponden a los valores 1, 5, 10, 50, 100, 500 y 1000. En cambio, en los países árabes, utilizaban el sistema numérico que se había perfeccionado en la India, entre los años 300 y 700, antes de nuestra era.

Fibonacci se dio cuenta que este sistema de numeración permitía trabajar con números de cualquier magnitud y que era mucho más sencilla la aritmética con él.

¿Sabes cómo se llama el sistema de numeración que se utiliza en la actualidad?

El sistema de numeración se conoce como sistema indo-arábigo, debido a que los árabes adoptaron este sistema, ideado por la cultura india, y fueron quienes lo dieron a conocer.

Ya tienes una imagen del contexto, ¿ya te ubicaste en esa época?

Ahora se hablará, de Leonardo de Pisa, quien fue hijo de Alessandra y Guglielmo Bonacci. Su padre fue funcionario consular en la aduana de Bugia, en Argelia, como ciudadano de la ciudad de Pisa, por este motivo Leonardo pasó gran parte de su infancia en este lugar.

Argelia es un país en el norte de África.

Cuando Leonardo tuvo edad para viajar, más o menos por el año 1192, aprendió la lengua árabe, la aritmética y conoció las ventajas de las matemáticas manejadas por esta cultura; es decir, con la numeración india, que los árabes habían adoptado en forma general, gracias al gran matemático Al Jwarizmi.

Imagina a este personaje, Leonardo de Pisa, observar la facilidad para hacer cálculos aritméticos. Debió quedar sorprendido y fascinado, sobre todo, porque la numeración enseñada por los árabes tenía, entre las muchas diferencias, la utilización del número cero, por ser un sistema de numeración posicional.

Si recuerdas, hasta el momento sólo se tienen registros de que la cultura india y la maya, fueron las únicas que incorporaron el número cero, ya que éste sirvió como notación posicional; es decir, que cada dígito posee un valor específico dependiendo de su posición.

Los árabes se enteraron de su utilidad en la escritura y en el cálculo de operaciones y fue otro motivo para adoptar este sistema numérico.

Leonardo recibió su primera formación matemática lejos de Europa, donde surge su entusiasmo e interés por estudiar a fondo esta ciencia; así que decidió viajar a otros países como Egipto, Siria, Grecia, Sicilia y Provenza. Es justo en Provenza donde conoció los tratados árabes de aritmética, gracias a la obra del matemático andaluz Juan de Sevilla, quien tradujo al latín una obra aritmética árabe en donde explicaban cómo realizar varios tipos de cálculos, con ayuda del ábaco y el sistema de numeración arábigo.

Leonardo regresó a Pisa en el año 1200 y comenzó a realizar sus propias aportaciones. Durante 25 años creó varias obras como: el Liber abaci, que significa “El libro del ábaco”.

Este libro trata principalmente de distintos problemas aritméticos aplicados a la vida real y con respecto al cálculo comercial, como lo relacionado al precio de mercancías, el cálculo de ganancias, la conversión de varias monedas y lo más importante: ayudó a la introducción de la numeración india.

Así es, ya no más cálculos complicados y cansados, para poder realizar operaciones largas; ahora, con una simple hoja de papel y un lápiz, podían hacer operaciones aritméticas.

Hay algo aún más fascinante, la famosa serie numérica que lleva su sobrenombre, sucesión de Fibonacci. Más adelante se explicará en qué consiste. Cabe mencionar que, para la creación de este libro, se basó en los conocimientos adquiridos durante sus viajes.

Ahora, se dará un dato curioso, y es que Leonardo de Pisa se autonombró Fibonacci, debido a la contracción de “Fili di Bonaccio”, por ser el hijo de Bonaccio, que era como conocían a Guglielmo el padre de Leonardo.

Otra de sus obras fue Practica Geometriae, que en español es geometría práctica, escrito en 1220. Es un tratado de problemas de geometría en donde se utilizan figuras planas y sólidas.

Una más de sus obras fue Flos super solutionibus quarumdam questionum ad numerum et ad geometriam pertinentium, parece un bonito trabalenguas, pero el título traducido al español, por supuesto, es más amigable de escuchar y es Ramillete de soluciones sobre cuestiones relativas al número y a la geometría.

La última obra que realizó fue Liber Quadratorum (El Libro de los Números Cuadrados), éste fue el libro más famoso de Fibonacci, porque surgió a través de un reto de un matemático llamado Teodoro de Antioquía, el cual era parte de la corte de Federico II.

Dice la historia, que Teodoro propuso encontrar un número cuadrado, de tal manera que, si se le restará o sumará cinco, el resultado fuera, en ambos casos, números cuadrados.

Y Teodoro no fue el único que lanzó retos matemáticos a Fibonacci. Johannes de Palermo, otro miembro de la corte de Federico II, le presentó varios problemas y, por supuesto, Fibonacci les dio solución junto con otros desafíos, los cuales fueron publicados en la obra Flos super solutionibus quarumdam, o, Ramillete de soluciones sobre cuestiones relativas al número y a la geometría.

Ahora, se hablará cómo es que Fibonacci dio a conocer la famosa sucesión de números a través de la resolución de un misterioso hábito de la reproducción de conejos.

Él planteó un problema que dice más o menos así:

Si es posible anota en tu cuaderno y pon mucha atención al siguiente problema:

Si se comienza con una pareja de conejos que reproduce cada mes otra pareja, que a su vez a los dos meses de vida puede procrear, ¿cuántas parejas de conejos se tienen al cabo de un año?

Parece un problema sencillo, pero hay que ir analizándolo con detenimiento:

Primero: La pregunta principal es ¿cuántas parejas de conejos habrá al cabo de un año?

Y el problema plantea que los conejos tardan 2 meses para comenzar a procrearse.

Además, en esta situación, imagina que es ideal, cuando la pareja se procrea, obtiene otra pareja de conejos que, a su vez, tardarán 2 meses en comenzar a procrearse. Y bueno, hay que aclarar, también, que las parejas que ya están maduras, continúan procreando.

Es así que se comienza con esta situación problemática ideal, con una pareja de conejos.

Se dice, que es una situación ideal, porque las variables nunca se van a modificar; por ejemplo: las parejas siempre tardarán 2 meses en procrear; de igual manera, de la reproducción se obtendrá una nueva pareja de conejos que tardarán, a su vez, 2 meses en reproducirse.

¿Ya sabes cuántas parejas habrá al cabo de un año? ¿Puedes responder al problema que planteó Fibonacci?

Con todas las premisas expuestas y contempladas, hay que ver paso a paso la resolución del problema:

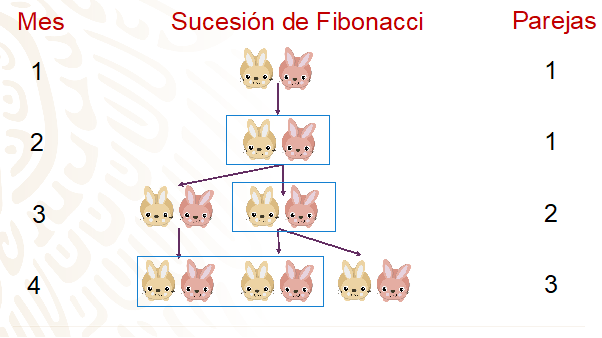
Sabes que en el primer mes hay una sola pareja de conejos, pero aún no está lista para procrear; por eso, en el segundo mes, aún sigue habiendo una sola pareja, aunque en este mes ya está madura y lista para procrear.

En el tercer mes, por primera vez se reproduce la pareja original, habiendo ahora 2 parejas de conejos: una pareja madura y la nueva pareja que acaba de nacer.

En el cuarto mes: la primera pareja de conejos vuelve a reproducirse, la segunda pareja aún no es lo suficientemente madura para ello; por lo que, en este mes, habrá 3 parejas de conejos: dos parejas maduras y una recién nacida.

¿Estás siguiendo la secuencia que lleva la sucesión?

Se espera que sí, hay que continuar con el problema:

En el quinto mes: la primera pareja vuelve a reproducirse, por lo que ya hay 4 parejas de conejos, pero no pierdas de vista que la segunda pareja, ya en este mes, se reproducirá por primera vez; entonces, ¿cuántas parejas de conejos se tendrán en el quinto mes?

Si, en el cuarto mes, se tienen 3 parejas, dos ellas ya se pueden reproducir; por lo tanto, en el quinto mes, habrá 4 parejas: las dos maduras y las dos recién nacidas, más una que ya maduro para reproducirse; por lo que, en el quinto mes, se tendrán en total 5 parejas: 3 parejas de conejos maduras y 2 recién nacidas.

Para el sexto mes, la primera y segunda pareja se vuelven a reproducir, mientras que la tercera pareja por primera vez se reproducirá; entonces, se tienen ahora ocho parejas de conejos; es decir, 5 parejas de conejos maduros y 3 recién nacidos.

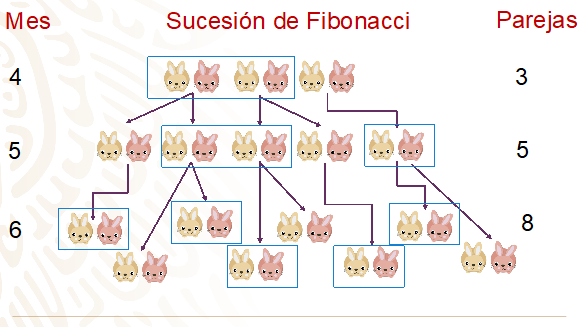
¿Ya sabes cuántas parejas habrá para el séptimo mes?

Si dijiste que 13 parejas de conejos, estás en lo correcto, porque se tendrán 8 parejas de conejos maduros y 5 recién nacidos.

¿Cuántas parejas de conejos habrá en 12 meses; es decir en un año?

La respuesta es 144 parejas de conejos.

Se te invita a continuar la sucesión, siguiendo el mismo patrón para comprobar que en un año habrá 144 parejas de conejos.

En el primer mes, sólo hay una pareja de conejos, en el segundo mes sigue habiendo 1 sola pareja; en el tercer mes, hay una pareja madura y la nueva pareja que acaba de nacer: en total 2 parejas; en el cuarto mes, hay dos parejas maduras y una recién nacida: en total 3 parejas. ¿Lo tienes?

En casa, sigue la secuencia, considerando la sucesión de números que se genera, verás que es muy interesante y bella esta serie.

Continuando con este patrón y, para el doceavo mes, son 55 y 89; en total, 144 parejas

Por lo que la sucesión quedaría de la siguiente manera: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…, y así se puede continuar, ya que es una sucesión de números infinitos.

¿Lograste identificar el patrón que sigue la sucesión?

La sucesión no es infinita; para que fuera infinita, los conejos deberían de ser inmortales, algo que no es posible.

Aunque antes ya se aclaró esta situación ideal, es decir, que los conejos nunca mueren y tampoco se enferman, y tampoco dejan de reproducirse, ni tienen más de 2 conejos por camada.

Pero analizando el patrón numérico que sigue. Como pudiste ver, en la sucesión numérica que se genera, cada número obtenido es igual a la suma de los dos anteriores. Por ejemplo, empieza con 1, como no hay número anterior, para el segundo término se considera la suma 0 + 1 = 1; el tercer término es igual a 1 + 1 = 2; el cuarto término es igual a segundo término más tercer término; es decir, 2 + 3 = 5. Y así sucesivamente todos los números.

Y, aunque esta sucesión es ideal aparentemente, no es tan imposible en la realidad, pues verás que, esta sucesión de números, te acompañan en la naturaleza.

Como en el caso de los pétalos de muchas flores, que forman espirales. Por ejemplo, Andrea una compañera tuya, tiene unas flores y contó sus pétalos, y el resultado fue este:

Tiene, uno, dos, tres, cuatro y cinco pétalos.

Esta otra tiene 1, 2, 3, 4, 5, 6, 7, 8 pétalos.

Nota que ambos números, el 5 y el 8 forman parte de la sucesión de Fibonacci.

El orden que tienen las semillas en un girasol, que crecen en forma de espiral; en la estructura de una alcachofa, también se presenta esta sucesión; y esta cualidad no solo está relacionada con las flores, también con las conchas del caracol, las pinturas e, incluso, las melodías de algunos músicos y compositores.

Aunque parezcan situaciones completamente alejadas entre sí, no lo son, todas ellas están relacionadas con la famosa sucesión de Fibonacci.

Otra peculiaridad que tienen los números de la sucesión de Fibonacci es que, si divides cada uno de los números que la integran, entre el número anterior, obtienes un resultado muy parecido, observa.

Al dividir uno entre uno, el resultado es uno; dos entre 1 igual a dos; tres entre dos, igual a uno punto cinco; cinco entre tres es igual a uno punto sesenta y seis; ocho entre cinco igual a uno punto seis; trece entre ocho igual a uno punto seiscientos veinticinco; veintiuno entre 13, es igual a uno punto seiscientos quince; y así puedes continuar obteniendo los cocientes, como puedes observar.

Si analizas los cocientes, mientras mayores son los números de las divisiones de esta sucesión, más se parecen los resultados. Esto sucede porque la sucesión de Fibonacci se encuentra íntimamente ligada al número áureo, ¿lo conoces?

El número dorado. Áureo, es una palabra en latín, que significa dorado o de oro. Y es un número irracional, tú ya conocías este tipo de números.

¿Recuerdas al número pi? ¡Sí! Aquel que usas para calcular el área o perímetro del círculo. ¡Ah! Pues éste es un número irracional, 3.1415926535897932384626433832.

Con esos números es suficiente, ya que nunca vas a acabar de mencionar las cifras decimales de pi, porque, al decir que es un número irracional, sabes que tiene un número infinito de decimales.

Es verdad y el número áureo o número de oro también está conformado por decimales infinitos. Para escribirlo se utiliza la letra phi y su valor es igual a: 1.61803398874989 y sigue de manera infinita.

Este descubrimiento del número áureo, se remonta a la época del Renacimiento, aunque se tienen motivos para creer que algunas construcciones egipcias y griegas se realizaron tomando como base este número.

Como sabes, el método para encontrar pi, es dividir el perímetro de un círculo entre su diámetro; al hacerlo llegas a encontrar una buena aproximación del famoso 3.1416…

Y para hallar el número dorado phi, también hay un medio.

Puedes anotarlo y tratar de encontrar el enigmático número áureo. ¿Estás lista o listo? Bueno, toma una regla. Dibuja un segmento de recta de longitud “a”, prolóngalo de manera que traces otro segmento más pequeño de longitud “b”.

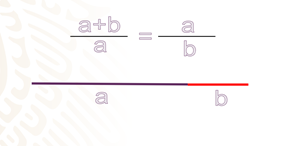
Si te preguntas de qué medidas deben ser estos segmentos de recta a y b, pues es sencillo, lo único que deben cumplir es que, al sumar la longitud de “a” más “b” y dividirla entre “a”, obtengas el mismo resultado que al dividir “a” entre “b”.

A lo que acabas de establecer, se le conoce como proporción. Ahora, lo importante es encontrar qué medidas en los segmentos cumplen con estas características; y es que las medidas de estos segmentos de recta, no son cualquier número.

Tú ya sabes de quién se está hablando ¿verdad?

De Fibonacci.

Y es que, si tomas cualquier par de valores consecutivos de la serie de Fibonacci, para verificar que se cumple esta proporción, observarás que es así; y, entre más grandes tomes los valores de la sucesión, la igualdad se cumple con mayor precisión.

Toma el par de valores 8 y 5, recuerda que son parte de la sucesión de Fibonacci. Dibuja un segmento de 8 cm, el siguiente segmento de 5 cm y realiza la proporción.

8 más 5 entre 8, y 8 entre 5.

8 más 5 es igual a 13, entonces hay que dividir 13 entre 8 y obtienes 1.625, posteriormente divides 8 entre 5 y obtienes 1.6. Observa que los valores de ambas razones son muy parecidos.

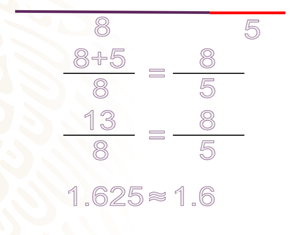
Observa que obtienes dos valores muy cercanos, casi se podría decir que son proporcionales, y es que así va a suceder con los valores de la serie de Fibonacci. Toma dos de los valores más grandes que viste aquí, y observa qué pasa.

Imagina que haces el segmento de recta de 21 centímetros y el otro de 13 centímetros. Ahora, para realizar la proporción sumas 21 más 13 y obtienes 34 que divides entre 21 y por otro lado divides 21 entre 13; así obtienes los resultados 1.61904 y 1.61538, que, como puedes observar, ya son prácticamente iguales.

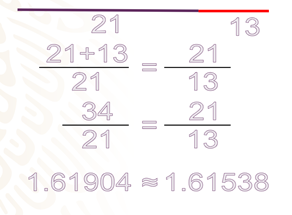
¿Recuerdas las divisiones que hiciste hace un momento con los diferentes valores de la sucesión de Fibonacci? Bueno pues, acabas de ver otra relación entre Fibonacci y el número áureo.

Pero espera, no termina ahí, y es que verás otra forma de organizar la sucesión de Fibonacci, que es muy interesante. Puedes observar la siguiente construcción, y hacer una réplica, verás qué sencilla y elegante se observa.

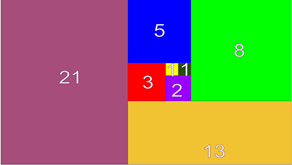
Dibujas un cuadrado que mida 1 centímetro de lado, a su lado derecho dibujas otro cuadrado idéntico de 1 centímetro de lado, debajo de ellos un cuadrado de 2 centímetros, a su izquierda un cuadrado de 3 centímetros, y, siguiendo este proceso, el siguiente cuadrado será de 5 centímetros y estará sobre los demás; continuarás con uno más, al lado derecho, esta vez de 8 centímetros y podrás continuar de la misma manera, mientras tengas espacio en tu hoja o podrías utilizar una cartulina.

Y la sucesión de Fibonacci, ¿La viste? Observa.

1, 1, 2, 3, 5, 8, 13, 21, y, si el plano lo permite, podrás continuar con la sucesión. Aunque no termina ahí, si tú trazas un cuarto de circunferencia apoyándote en las esquinas de cada cuadrado, observarás que se crea una bonita espiral.

Observa cómo vas trazando arcos con centro en cada uno de los vértices de tus cuadrados con radio, 1, 1, 2, 3, 5, 8, y así sucesivamente.

Esta espiral, es también conocida como, espiral Áurea y puede ser encontrada en la naturaleza, en lugares como la concha del nautilus, en las formaciones de las galaxias, en los huracanes.

Grandes artistas han recurrido a la proporción áurea para realizar sus obras; tal es el caso del Partenón griego, La Gioconda y Las meninas.

Leonardo de Pisa, mejor conocido como Fibonacci, no sólo trajo al mundo occidental un nuevo método efectivo para realizar operaciones aritméticas, al usar y promover el uso del sistema indo arábigo de numeración. Sino que también acercó a las personas a aspectos por demás bellos de las matemáticas, al estudiar su famosa sucesión.

Ahora ya sabes, que las matemáticas tienen su historia y conocerla te proporciona una perspectiva interesante.

Has concluido el tema del día de hoy.

El reto del hoy:

Se te propone que busques otros lugares donde la sucesión y el número áureo puedan ser encontrados. Tal vez descubras que, incluso en el cuerpo humano, el número dorado se hace presente.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html