Fracciones y decimales positivos y negativos
Fracciones y decimales positivos y negativos
Aprendizaje esperado: resuelve problemas de suma y resta con números naturales, fracciones y decimales positivos y negativos.
Énfasis: sumar y restar fracciones y números decimales, positivos y negativos.
¿Qué vamos a aprender?
En esta sesión emplearás diversos contextos, tanto de la vida cotidiana como algunos juegos matemáticos, a modo de consolidar los procedimientos para sumar y restar fracciones y números decimales, positivos y negativos.
¿Qué hacemos?
En lecciones anteriores revisaste la resolución de algunos problemas en los que fue necesario emplear la suma de fracciones y números decimales, positivos y negativos. En esta sesión se continuará trabajando este tema. Si tienes alguna duda, no te preocupes, regístralas en tu cuaderno y en esta sesión se irán resolviendo.
Para iniciar analiza el siguiente planteamiento.
Juan es buzo y se sumerge en el mar, cerca de un arrecife, para recoger muestras de vida. Para tomar su primera muestra, desciende 1 metro y 3/5; luego, por razones de seguridad, Juan debe ascender medio metro. Para tomar la segunda muestra debe descender 3 metros y 2/5: ¿a qué distancia de la superficie está cuando tomó la segunda muestra?

Para responder a la pregunta, se debe representar con números negativos los descensos y con números positivos los ascensos, con ello se tiene: 1 3/5 negativo para el primer descenso; 1/2 positivo para el ascenso; y 3 2/5 negativo para el segundo ascenso.
¿Qué procedimiento debes seguir para determinar la posición final de Juan?
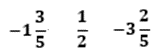
Para calcular a qué distancia de la superficie está Juan debes considerar que primero estaba a menos 1 metro y 3/5 de metro y ascendió medio metro; entonces, para saber a qué distancia estaba en ese momento, sumas: un entero 3/5 negativo más un medio.
Lo primero que hay que hacer es convertir 1 entero 3/5 negativo a fracción impropia, es igual a 8/5 negativo.
Para sumar las fracciones buscas un factor común para obtener fracciones con igual denominador.
¿Cuál piensas que sería ese denominador?
En este caso, el común denominador es 10. Anota la suma con las fracciones equivalentes: 16/10 negativo más 5/10 es igual a:

¿Qué tienes que hacer para resolver la adición?
Como una de las fracciones de esta adición es positiva y la otra negativa, el procedimiento a seguir es encontrar la diferencia entre sus valores absolutos.
16/10 menos 5/10 es igual a 11/10. Ahora, 16/10 negativo tiene mayor valor absoluto, 16 décimos negativo más 5 décimos, es igual a 11/10 negativo, que representa, en metros, la posición de Juan después de su ascenso.

Ahora, considera que, en el segundo descenso, que fue de 3 metros y 2/5 de metro, conviertes el número mixto a fracción impropia y, después, a una fracción equivalente con denominador 10; 17/5 negativo es igual a 34/10 negativo.
Resuelve la adición resultante: 11/10 negativos más 34/ décimos negativos es igual a 45/10 negativos.

Así, obtienes la respuesta. Sabes que Juan se encontraba a 45/10 de metro negativo de la superficie, al obtener la segunda muestra, que equivale a 4 1/2 metros bajo el nivel del mar.
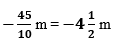
Después de este ejercicio que te permitió recuperar tus conocimientos sobre la solución de sumas y restas de fracciones y de números positivos y negativos, resolverás las siguientes actividades. Recuerda tomar nota de la información.
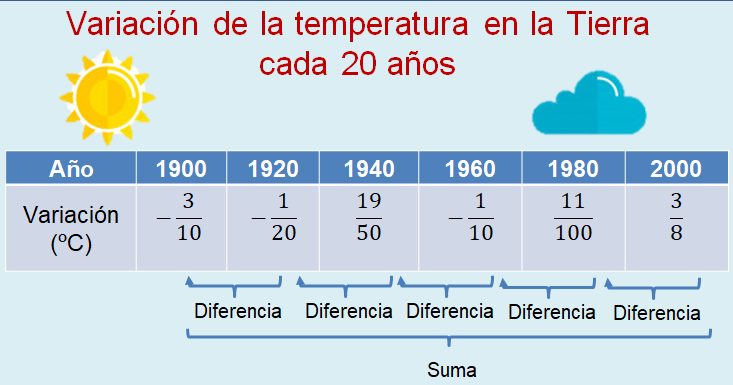
El calentamiento global consiste en el aumento de la temperatura de la Tierra, mismo que se refleja en los océanos y la atmósfera; principalmente, es causado por la emisión de gases de efecto invernadero, expedidos por la actividad humana. Debido a las graves consecuencias de este problema se ha estudiado con detenimiento desde inicios del siglo XX. Enseguida, revisarás en una tabla el registro de la variación promedio de la temperatura, experimentada cada 20 años en todo el planeta.
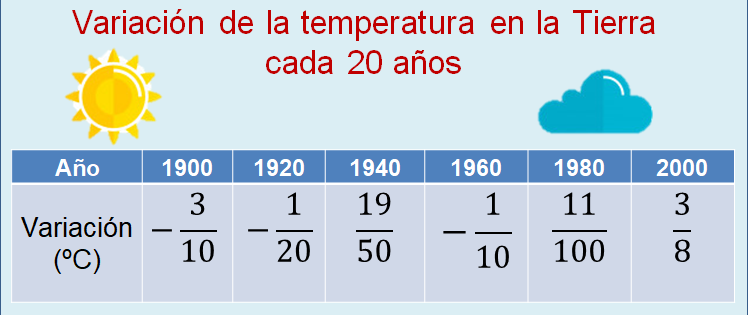
Puedes ver que, en 1900, la variación de la temperatura fue de 3 décimos negativos de grado Celsius; lo que significa que disminuyó; en 1920, la variación promedio fue de un vigésimo negativo; en 1940 la temperatura aumentó, en promedio, diecinueve cincuentavos de grado; en 1960 varió un décimo negativo; en 1980 aumentó once centésimos de grado y, en 2000, también aumentó tres octavos de grado.
La situación te lleva a plantear distintas preguntas. ¿Cuál fue la diferencia entre la variación de la temperatura entre 1900 y 1940?
Como pudiste observar, el registro de la variación, en 1900, fue de 3 décimos negativos de grado Celsius, mientras que en 1940 fue de diecinueve cincuentavos. Para encontrar la diferencia en la variación de temperatura que hubo entre estos dos años tienes que resolverlo con una resta. Debes tomar el registro de la temperatura promedio de 1940 y le restas el registro de 1900; esto es: 19/50 menos 3/10 negativo.
Para resolver la operación aplicas las reglas de la sustracción de números positivos y negativos, que te indican que restar es lo mismo que sumar por el opuesto o inverso aditivo del sustraendo.
En este caso, el número opuesto de tres décimos negativo es tres décimos, por lo que la suma correspondiente sería: 19/50 + 3/10.
Para resolver esta suma debes expresar ambos sumandos con el mismo denominador; para hacerlo tienes que convertir 3/10 a su fracción equivalente 15/50.
Ahora sí, sumas 19/50 + 3/10 = 19/50 + 15/50. Al resolver la operación, el resultado es 34/50.
Treinta y cuatro cincuentavos pueden simplificarse, y te queda: 17/25.

La diferencia en la variación de la temperatura entre el año 1900 y 1940 fue de diecisiete veinticincoavos de grado Celsius.
Considera que no calculaste la variación total, únicamente la diferencia entre los valores de estos años.
Ahora, revisa la diferencia entre la variación de la temperatura de los años 1900 y 2000. Considera que sólo vas a calcular la diferencia entre esos años, no la variación total del siglo.
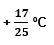
Como puedes observar en la siguiente tabla, el registro de la variación en 1900 fue de 3 décimos negativos de grado, mientras que en 2000 fue de diecinueve cincuentavos de grado Celsius. Para encontrar la diferencia en la variación de temperatura entre estos dos años, recurrirás a una sustracción.

Esto es, 3/8 – (–3/10).
Para resolverla conviertes la resta en una suma, cambiando el sustraendo por su inverso aditivo, por lo que te queda la suma 3/8 + 3/10.
Tienes que convertir las fracciones a fracciones equivalentes con igual denominador que, en este caso, será 40. Obteniendo las fracciones 15/40 y 12/40, respectivamente.
Entonces, te queda como: 3/8 + 3/10 = 15/40 + 12/40 = 27/40.
Observa que la diferencia de la variación, entre estos dos años, fue de 27/40 grados Celsius.
Hay que revisar otra situación:
Los cuadrados mágicos son juegos matemáticos creados por Luca Pacioli en el siglo XIV. De este ilustre matemático ya se ha hablado recientemente en Aprende en casa III.

Para seguir practicando la suma y resta de fracciones positivas y negativas hay que completar un cuadrado mágico de 3 por 3. Como debes recordar, para completar un cuadrado mágico, la única regla es que todas las sumas: horizontales, verticales y diagonales lleven al mismo resultado. ¿Lista o listo?
Observa el siguiente cuadro mágico.

En este caso la suma de filas, columnas y diagonales tiene que ser de ½ negativo. Para completarlo se comenzará con la columna de la izquierda que muestra dos valores: un tercio y un tercio negativo.
Como has visto antes, estas fracciones representan números opuestos. ¿Recuerdas qué sucede al sumar números opuestos?
Efectivamente, el resultado es cero; entonces, solamente tienes que agregar la fracción un medio negativo para completar la columna y cumplir con la suma.
El valor encontrado forma parte de la segunda fila, junto con un sexto negativo. Como en esta fila aparece la suma que necesitas, es decir, 1/2 negativo, entonces buscas un número que sumado a 1/6 negativo te dé cero; que en este caso es su opuesto, es decir, 1/6.
¿Cómo vas hasta aquí?
Recuerda tomar nota para después comprobar los resultados. Hay que continuar.
Ahora, se debe completar la diagonal que contiene 1/3 negativo y 1/6 negativo, sumas sus valores absolutos y el resultado será un número negativo. 1/3 negativo es igual a 2/6 negativo; entonces, 2/6 negativo más 1/6 negativo igual a 3/6 negativo, que es igual a un medio negativo.
Con esto, ya tienes el número que buscas, 1/2 negativo. Para no alterar el resultado, únicamente agregas el cero. Puedes comprobarlo restando 3/6 negativo menos 3/6 negativo, que es lo mismo que sumar por el opuesto, 3/6 negativo más 3/6 igual a cero.
Completas la primera fila. A 1/2 negativo le restas 1/3 para encontrar el valor que falta. Como restar es lo mismo que sumar por el inverso aditivo, operas con fracciones equivalentes como sextos: 3/6 negativo más 2/6 negativo es igual a 5/6 negativo.
A continuación, hay que realizar la segunda columna.
Sumas 5/6 negativo más 1/6 negativo, que es igual a 6/6 negativo, igual a 1 negativo.
Para encontrar la fracción que falta restas 1/2 negativo menos 1 negativo, que es igual a la suma 3/6 más 6/6, que es igual a 3/6 igual a 1/2.
Sólo te falta una casilla.
Para que sea más sencillo, considera la tercera columna. A 1/2 negativo le restas 1/6, operas con sextos y aplicas la regla de la sustracción, sumando 1/2 negativo más el opuesto de 1/6, que es 1/6 negativo, que es igual a 4/6 negativo.

Has terminado con la actividad del cuadrado mágico. Se espera que te haya resultado útil para poner en práctica los procedimientos de la adición y sustracción de fracciones y las reglas al operar con números positivos y negativos.
Para continuar practicando, hay que resolver la siguiente situación.
El precio del dólar es un tema que a diario ves en los noticieros, periódicos o en las casas de cambio y bancos. Es un tema de gran importancia que debes tener presente, ya que su valor está directamente relacionado con el costo de muchos productos y servicios de origen extranjero, que se consumen en el país.
En la tabla siguiente se muestra cuánto varió el precio del dólar, con respecto al peso mexicano, durante siete días. Observa.
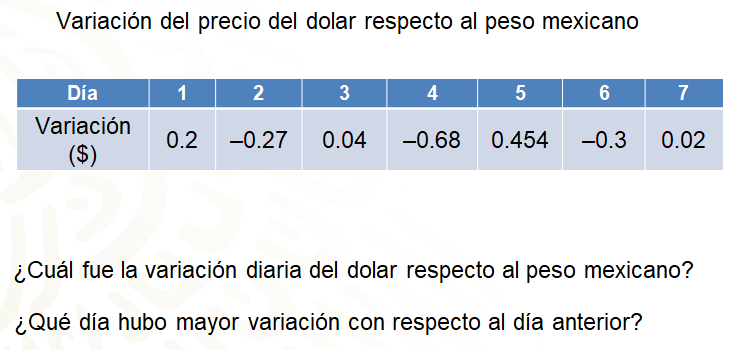
Para dar respuesta a las preguntas es necesario comparar el precio del dólar de un día para otro; esto es, la variación que hubo entre los días consecutivos.
¿Qué operación te permite hacer esas comparaciones?
Una resta. A la variación de cada día se le resta la variación del día anterior.
Ahora hay que resolver las operaciones, aplicando las reglas de la sustracción de números positivos y negativos.
Hay que empezar con la comparación entre los días 1 y 2.
El día 1 la variación fue de 0.2, mientras que en el día 2 fue de -0.27, por lo que la resta que se genera es: 0.27 negativo menos 0.2. Al resolver la operación, el resultado es 0.47 negativo.
¿Puedes explicar por qué?
Al aplicar la regla de la sustracción, se convierte la resta en una suma de números negativos.
Así se tiene que 0.27 negativo más 0.20 negativo es igual a 0.47 negativo.
El resultado te indica que la variación que hubo entre el día 1 y 2 fue de –0.47.

Compara, ahora, la variación entre los días 2 y 3.
El día 2 se registró una variación de – 0.27, en tanto que en el día 3 fue de 0.04, por lo que la resta que se genera es: 0.04 – 0.27 negativo.
Al escribir la resta como una adición se obtiene una suma de dos números positivos. Al resolverla mediante el algoritmo, el resultado es 0.31.
Lo que te indica que la variación que hubo entre el día 2 y 3 fue de $0.31.

Ahora hay que ver sucedió entre el día 3 y el día 4.
En este caso la resta que se genera es 0.68 negativo menos 0.04. Al aplicar la regla de la sustracción, la conviertes en una suma de dos números negativos: 0.68 negativo más 0.04 negativo.
Al resolver la operación el resultado es 0.72 negativo, lo que te indica que la variación que hubo entre los días 3 y 4 fue de – 0.72.
¿Cómo vas en casa? ¿Tienes claros los procedimientos para restar números positivos y negativos?

Hay que revisar la siguiente comparación, días 4 y 5.
El día 4 hubo una variación de – 0.68, en tanto que en el día 5 fue de 0.454, por lo que la resta que se genera es: 0.454 menos 0.68 negativo, que es igual a la suma 0.454 + 0.68. Al resolverla de la manera que ya conoces, el resultado te indica que la variación que hubo entre los días 4 y 5 fue de $1.134.

Aunque en términos de la realidad esa cantidad de dinero no es posible representarla.
Ahora, se obtendrá la variación que hubo entre el día 5 y el día 6.
El día 5 se registró una variación de 0.454 pesos, mientras que en el día 6 fue de 0.3 pesos negativos, por lo que la resta que se genera es: 0.3 negativo menos 0.454, que al convertirla en una suma equivalente se tiene: 0.3 negativo más 0.454 negativo es igual a 0.754 negativo.
El resultado te indica que la variación que hubo entre los días 5 y 6 fue de $0.754 negativos.

Finalmente, hay que comparar lo sucedido entre los días 6 y 7. El día 6 hubo una variación de $0.3 negativos, en tanto que en el día 7 fue de $0.02, por lo que la resta que se genera es: 0.02 menos 0.3 negativo. Pasas a una suma, empleando el inverso aditivo del sustraendo, que es 0.3 para tener la suma: 0.02 + 0.3, cuyo resultado es 0.32.
El resultado te indica que la variación que hubo entre el día 6 y el día 7 fue de $0.32.

Ya tienes el precio del dólar respecto al peso mexicano de todos los días de la semana, con eso se dio respuesta a la primera pregunta. Ahora, sólo falta determinar qué día hubo mayor variación. Hay que concentrarse en las comparaciones obtenidas en una tabla para dar respuesta a la segunda pregunta planteada: ¿cuál fue la mayor variación que hubo en dos días consecutivos?

Es la mayor variación, sin importar si es positiva o negativa, porque es el número que tiene el mayor absoluto. Esto te lleva a identificar que, entre los días 2 y 3, se dio la menor variación, ya que 0.31 es el número con menor valor absoluto.
Ahora, ¿qué te parece si tomas un momento para anotar lo más importante del tema que se desarrolló el día de hoy?
|
En caso de que tengas dudas o desees profundizar o practicar lo visto en esta sesión, se te recomienda apoyarte en tu libro de texto de Matemáticas de primer grado; o bien, volver a ver esta lección.
Has concluido el tema del día de hoy.
El reto de hoy:
Ahora, se te invita a realizar el siguiente reto, calcula la variación total de la temperatura durante el siglo XX, es decir, de 1900 a 2000.
Para ello, tienes que calcular la diferencia entre periodos consecutivos de 20 años y, al final, sumar esas diferencias.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas