Ecuaciones lineales
Ecuaciones lineales
Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de ecuaciones lineales.
Énfasis: resolver y plantear problemas de ecuaciones lineales.
¿Qué vamos a aprender?
En esta sesión ampliarás tus los conocimientos sobre cómo “Resolver y plantear problemas de ecuaciones lineales”. Realizarás ciertas actividades que te permitirán precisar algunas peculiaridades sobre este tema.
Toma nota de cada una de las actividades que se desarrollarán. ¡Pon mucha atención, ya que comenzarás con otra aventura llena de conocimientos!
Se tomarán algunos contextos que serán necesarios utilizar para la comprensión del tema a tratar. Profundizarás en el uso de los procedimientos para resolver problemas, aprovechando situaciones que puedes ubicar en la vida cotidiana.
Para lograr un mejor desempeño al realizar las actividades, te recomiendo tener siempre cerca de ti:
- Tu cuaderno, o bien, hojas reutilizables
- Lápiz
- Goma
- Y tú libro de texto de la asignatura de Matemáticas de primer grado, como apoyo.
Aprenderás a resolver ecuaciones de la forma “ax + b = cx + d”.
¿Qué hacemos?
Comienza con la siguiente situación.
Ya sabes que una igualdad es la equivalencia entre dos expresiones conectadas a través del signo igual.
La relación de igualdad se emplea para denotar que dos objetos matemáticos expresan el mismo valor.
Por ejemplo, la expresión: 2 + 3 = 3 + 1 + 1, representa una igualdad. Pero ¿qué sucede si del lado izquierdo de la igualdad restamos 3?
En este caso, la igualdad ya no se cumple, porque, 2 + 3 – 3 no es igual a 3 + 1 + 1.
¿Qué tienes que hacer del lado derecho para que se conserve la igualdad?
Para que la igualdad se conserve, también tienes que restar 3 del lado derecho, para obtener la expresión: 2 + 3 – 3 = 3 + 1 + 1 – 3.
Que, al simplificar, puedes corroborar; ya que 2 es igual a 1 + 1, igual a 2.
Esto mismo sucede al resolver una ecuación. Como ya sabes que una igualdad entre dos expresiones algebraicas se conserva; siempre y cuando suceda lo mismo en ambas partes de la igualdad.
Ve cómo se aplica lo visto en el ejemplo, para resolver una ecuación con el siguiente problema.
“Alejandro y Claudia se inscribieron a un club, con el fin de poder aprender a jugar tenis. El primer día de entrenamiento, a Alejandro le entregaron 5 cajas con pelotas de tenis, más tres pelotas sueltas; y a Claudia le entregaron dos cajas con pelotas de tenis, más 9 pelotas sueltas. Alejandro le preguntó al entrenador por qué a su amiga Claudia le había entregado más pelotas, quien le respondió que ambos tenían el mismo número de pelotas para entrenar, porque todas las cajas tenían el mismo número de pelotas.
¿Puedes ayudar a Alejandro y a Claudia a verificar el número de pelotas de tenis que les entregaron sin tener que abrir las cajas?”
Inicia planteando la situación mediante una ecuación.
En este caso, se desconoce la cantidad de pelotas que tiene cada caja; por lo que las cajas las representamos con “x”; es decir, será la incógnita de la ecuación que se plantea.
Alejandro tiene 5 cajas de pelotas más 3 pelotas sueltas que se representa con la expresión: 5x + 3
Claudia tiene 2 cajas de pelotas más 9 pelotas sueltas que se representa con la expresión: 2x + 9
Dado que la cantidad de pelotas que les dieron a ambos es la misma, unimos ambas expresiones con el signo igual y se obtiene la ecuación: 5x + 3 = 2x + 9
Bien, observa que la ecuación representa una igualdad entre sus miembros, a semejanza de lo que observas en el ejemplo de las operaciones aritméticas. Por lo tanto, lo que se hace de un lado de la igualdad: sumar, restar, multiplicar o dividir, tienes que hacerlo en ambos lados para conservar la igualdad.
Por medio de esquemas puedes resolver el problema y, posteriormente, lo representarás algebraicamente.
Observa lo siguiente.
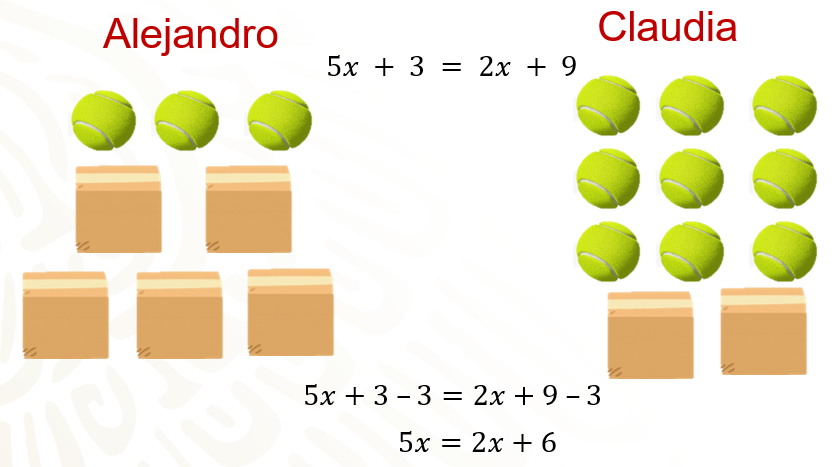
Primero, quita las tres pelotas sueltas que hay del lado izquierdo y, para conservar la igualdad, quita las mismas tres pelotas del lado derecho, te quedan 5 cajas del lado izquierdo y, del lado derecho, 6 pelotas y 2 cajas. Algebraicamente, restas 3 en ambos miembros de la igualdad obteniendo la expresión 5x + 3 – 3 = 2x + 9 – 3; al simplificar te queda como: 5x = 2x + 6, que coincide con la representación gráfica que se hizo.
¿Cuál sería el siguiente paso para saber cuántas pelotas hay en cada caja y saber cuántas pelotas recibió cada uno?
Para poder conocer cuántas pelotas tiene cada caja, tienes que encontrar el valor de “x”; es decir, se requiere “despejar” a x, esto es dejarla “sola” de un lado de la igualdad.
Debe quedar una sola caja.
Otra manera de reducir más términos. En este caso, una posibilidad es retirar dos cajas de pelotas de cada lado de la balanza, para no perder la igualdad.
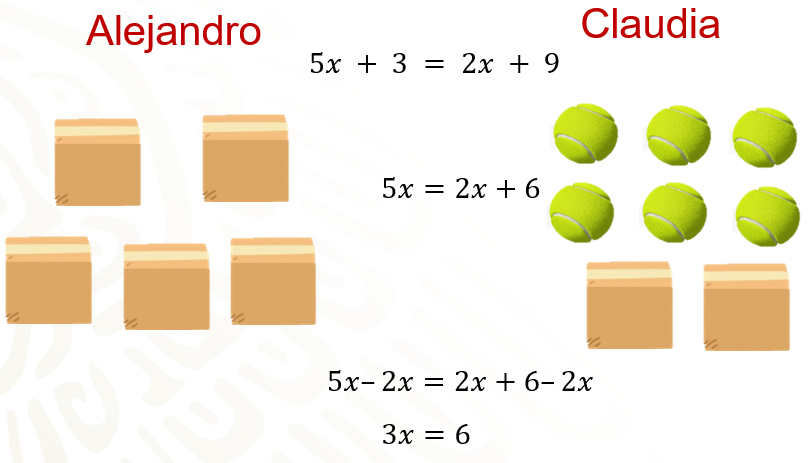
Se tiene ahora, del lado izquierdo, 3 cajas de pelotas de tenis y, del lado derecho, 6 pelotas de tenis sueltas. Algebraicamente, se tiene: 5x – 2x = 2x + 6 – 2x, y al simplificar la ecuación queda como: 3x = 6.
¿Qué se tiene que hacer ahora para saber cuántas pelotas hay en cada caja?
Al observar la imagen, puedes deducir que cada caja tiene dos pelotas en ellas. ¿No quedó claro?
Observa qué sucede.
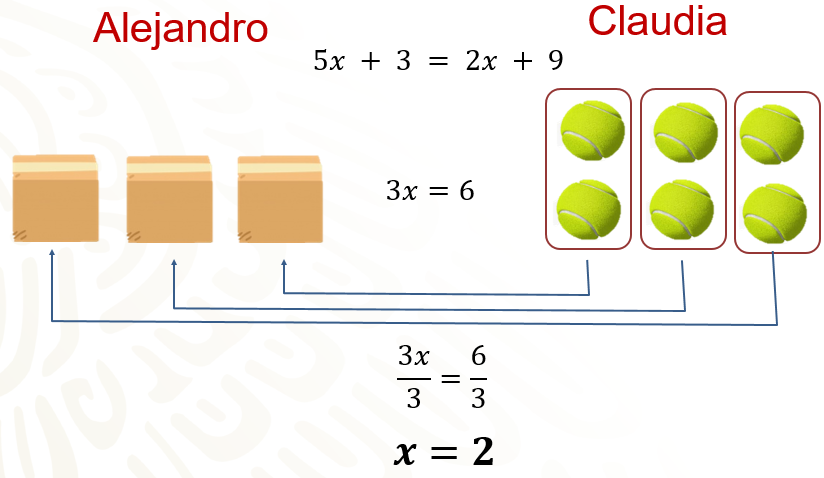
Del lado izquierdo se observa que a Alejandro le quedan 3 cajas de pelotas y a Claudia seis pelotas sueltas. Al tener ambos la misma cantidad de pelotas y, sabiendo que las cajas tienen el mismo número de pelotas, se puede deducir que cada una tiene dos.
Entonces, algebraicamente, para obtener la cantidad de pelotas que tiene cada caja, se divide 3x entre 3.
Para que se conserve la igualdad, se debe dividir, también entre 3, el 6 del lado derecho de la igualdad, cuyo resultado es igual a 2. Es decir, el valor desconocido de la “x”. Esto es que el contenido de cada caja 2 pelotas de tenis.
Se comprueba el resultado para tener la seguridad de que el valor encontrado de la incógnita, en este caso de “x”, cumple con las condiciones establecidas en el problema. Y así, saber cuántas pelotas recibieron Alejandro y Claudia,
Para ello, se sustituye el valor encontrado de “x” en la ecuación original como sigue: 5x + 3 = 2x + 9.
Quedando la igualdad: 5(2) + 3 = 2(2) + 9.

Al resolver las operaciones, aplicando la jerarquía, se obtiene: 10 + 3 = 4 + 9
Al simplificar observa que 13 = 13.
Lo que significa que, al obtener la igualdad, se corrobora que el valor de “x” es el correcto, por lo que cada caja contiene 2 pelotas de tenis.
¿Cuántas pelotas recibió cada uno?

Para encontrar el resultado, sabiendo que cada caja tiene 2 pelotas y que Alejandro recibió 5 cajas y 3 pelotas sueltas, se tiene que 5 por 2, más 3, es igual a 10 más 3, igual a 13. En el caso de Claudia, ella recibió 2 cajas y 9 pelotas sueltas; por ello se resuelve la operación 2 por 2 más 9, que es igual a 4 más 9 igual a 13.
Con esto, se obtiene que ambos recibieron la misma cantidad de pelotas: 13.
Te propongo el siguiente reto, para confirmar tus avances en la comprensión de este tema.
Toma nota de la información que sea necesaria, para platear la ecuación y resolver el problema.
“Enrique y Jaime trabajan en un almacén.
Ambos tienen que guardar la misma cantidad de latas de jugo en cajas; para, después, apilarlas en la bodega del almacén.
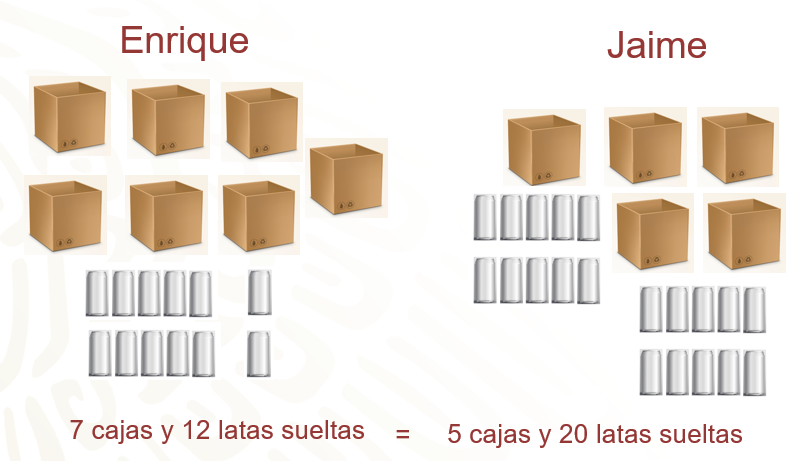
Enrique llenó 7 cajas y le falta guardar 12 latas. A Jaime le faltan 20 latas y ya completó 5 cajas.
¿Cuántas latas tiene cada caja? ¿Cuántas latas tiene que guardar cada uno?”
Bien, ahora se establece la ecuación que representa el problema, para responder las preguntas anteriores.
¿Puedes obtener las expresiones algebraicas que representan la información de Enrique y Jaime? Escríbelas en tu cuaderno.
Verifica que sean iguales a las siguientes:
Enrique: 7x + 12
Jaime: 5x + 20
¿Obtuviste las mismas expresiones?
A continuación, se usan las expresiones anteriores y se establece la ecuación del problema. Hazlo en tu cuaderno.
La ecuación obtenida es:
7x + 12 = 5x + 20
Observa que se expresa con “x” la incógnita a despejar, y que representa el número de latas que hay en cada caja.
Resuelve la ecuación. Ten presente que, para resolverla, se despeja la incógnita.
Se inicia con la eliminación del término independiente del miembro izquierdo; para ello, se resta esa cantidad en ambos lados de la igualdad. Al aplicar las propiedades de la igualdad matemática, cuando se suma o resta una cantidad en un miembro de la ecuación, se debe sumar o restar la misma cantidad del en el otro miembro.
Se tiene que
7x + 12 – 12 = 5x + 20 – 12
Al realizar las operaciones para simplificar, se obtiene
7x = 5x + 8
Con el fin de despejar la incógnita, reduciéndose reducen los términos semejantes. En este caso, los términos semejantes con la literal “x”. Observemos que se debe eliminar 5x en el lado derecho de la igualdad, para que se tenga la incógnita en el lado izquierdo.
¿Cómo se elimina 5x del lado derecho de la igualdad? Restando 5x en ambos lados, para eliminar este término del lado derecho y que nos quede sólo el término independiente. Entonces se tiene que:
7x – 5x = 5x – 5x + 8
Al simplificar la expresión, se tiene: 2x = 8
Para despejar a “x”, aplicamos nuevamente una propiedad de la igualdad.
¿Qué se debe hacer para despejar a “x” en el miembro izquierdo? Dividir entre 2, ya que 2x entre 2 es igual a “x”; pero, al dividir el miembro izquierdo entre 2, se debe hacer también en el miembro de la derecha.
2x entre 2 = 8 entre 2
Y al realizar las operaciones, se tiene que: x = 4.
Lo anterior significa que, en cada caja, hay 4 latas de jugo.
Se comprueba el resultado, sustituyendo en la ecuación el valor obtenido de la incógnita.
Puedes hacer la comprobación en tu cuaderno para validar que la solución de la ecuación es correcta.
Observa si lo que hiciste es semejante a esto:
7x + 12 = 5x + 20
7(4) + 12 = 5(4) + 20
28 + 12 = 20 + 20
40 = 40
Dado que ya se comprobó que el valor de la incógnita es igual a 4, se puede decir que cada caja contiene 4 latas; con lo que se da respuesta al problema planteado. Una información adicional que puedes concluir es que Enrique y Jaime empacaron 40 latas en total.
Para ahondar en la resolución de problemas que llevan a ecuaciones de la forma ax + b = cx + d, analiza y resuelve la siguiente situación.
“Julieta tenía 2 000 pesos ahorrados en su cuenta bancaria y ayer hizo un depósito de cierta cantidad. Juan tenía en su cuenta el triple de lo que Julieta depositó, e hizo un retiro de 1 000 pesos. Después de estos movimientos, las cuentas bancarias de ambos tienen la misma cantidad de dinero.
¿Cuánto dinero depositó Julieta?, ¿cuánto dinero tenía originalmente Juan en su cuenta?, ¿cuánto dinero tienen en su cuenta?”
Muy bien, después de leer detenidamente el planteamiento, debes establecer las expresiones algebraicas que representan los movimientos de Julieta y Juan, en su cuenta bancaria.
Te recomiendo que vayas tomando nota en tu cuaderno.
En este caso, se desconoce cuánto dinero depositó Julieta; por lo que, por ser un valor no conocido, se indicará con la literal “x”. Ya sabes que puedes utilizar también las literales “y” o “z”, que se usas comúnmente para indicar a una incógnita.
La expresión algebraica que representa lo relacionado con el dinero de Julieta es: 2 000 + x
Ya que originalmente tenía 2 000 pesos en su cuenta e hizo un depósito, que no se conoce a cuánto ascendió.
Para representar los movimientos de Juan, obtenemos la siguiente expresión algebraica
3x – 1 000
Según se plantea en el problema, tenía, inicialmente en su cuenta, el triple de lo que depositó Julieta, e hizo un retiro de 1 000 pesos.
Como se establece que, después de estos movimientos, los dos tenían la misma cantidad de dinero en sus cuentas, iguala las expresiones algebraicas para obtener la ecuación
2 000 + x = 3x – 1 000
A continuación, se aplican las propiedades de la igualdad, como en los casos anteriores para despejar la incógnita y resolver el problema.
Como has visto, debes eliminar términos para simplificar la ecuación, con el fin de ir despejando la incógnita. En este caso, iniciarás con la eliminación del término independiente del miembro derecho, esto con el fin de operar con números positivos; se suma 1 000 en ambos miembros, con lo que se tiene lo siguiente:
2 000 + 1 000 + x = 3x – 1 000 + 1 000
Al efectuar las operaciones señaladas queda:
3 000 + x = 3x
Se procede a reunir en el mismo miembro de la igualdad los términos que tienen a la incógnita. Para eliminar a “x” del lado izquierdo; restamos “x” en ambos miembros de la igualdad.
3 000 + x – x = 3x – x
Al realizar las operaciones resulta lo siguiente
3 000 = 2x
Muy bien, has logrado que la incógnita “x” se encuentre solamente en un miembro de la ecuación.
Para completar el despeje de la incógnita, observa que x está multiplicada por 2; por lo que debes dividir ambos miembros de la ecuación entre 2,
3 000 entre 2 = 2x entre 2
Al realizar las divisiones resulta que x es igual a 1 500.
Una vez que se ha encontrado el valor de la incógnita “x”, se comprueba que el valor obtenido es correcto en la ecuación inicial: 2 000 + x = 3x – 1 000.
Al sustituir el valor que se obtuvo de la x, se tiene que:
2 000 + 1 500 = 3 (1 500) – 1000
Al realizar la operación en el miembro izquierdo resulta que: 3 500 = 3 (1 500) – 1 000.
Al efectuar las operaciones en el miembro derecho se tiene que: 3 500 = 4 500 – 1000
Por lo que se obtiene finalmente: 3 500 = 3 500
Con lo que se comprueba que el valor encontrado de x, es correcto.
Así se obtiene que Julieta depositó $1 500;
Juan tenía originalmente en su cuenta el triple de lo que depositó Julieta, esto es: 3($1 500) = $ 4 500
Julieta tiene en su cuenta:
2 000 + 1 500 = $3 500
Juan tiene en su cuenta:
4 500 pesos menos 1 000 pesos = 3 500 pesos.
El reto de hoy:
El reto será plantear un problema que se resuelva con dicha ecuación.
Toma nota en tu cuaderno.
La ecuación es: 13x – 7 = 7x + 11
¿Ya pensaste en la situación que podría representarse con la ecuación?
Resuelve la ecuación:
¿Qué es lo primero que hay que hacer?
Se tiene que despejar la incógnita en uno de los lados de la igualdad, en este caso, lo harás del lado izquierdo, como a 13x se le resta 7, entonces se suma 7 en ambos lados de la igualdad, obteniendo la expresión:
13x – 7 + 7 = 7x + 11 + 7, que al simplificar queda como:
13x = 7x + 18.
Ahora se resta 7x en ambos lados para tener a la incógnita únicamente del lado derecho, 13x – 7x = 7x + 18 – 7x, al simplificar queda como 6x = 18.
Finalmente, para despejar a la incógnita se divide entre 6 ambos miembros de la ecuación, resultando x igual a 3.
Comprueba que el resultado es el correcto, sustituyendo a “x” por el valor obtenido y resolviendo las operaciones. Si tienes oportunidad comparte con tu maestra o maestro tus resultados y el problema que inventaste para recibir retroalimentación.
Anota en tu cuaderno lo más importante de la sesión.
- Algunas situaciones de la vida cotidiana pueden resolverse mediante ecuaciones de primer grado.
- Es importante comprender la situación que se plantea y obtener la ecuación que la represente.
- Resolver la ecuación empleando la propiedad uniforme de la igualdad, para despejar la incógnita.
- Comprobar que el valor de la incógnita que se obtenga es correcto, sustituyéndolo en la ecuación original.
- Responder a las preguntas que se hacen en el planteamiento de la situación.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas