Divisiones equivalentes I
Divisiones equivalentes I
Aprendizaje esperado: resuelve problemas de multiplicación con fracciones y decimales y de división con decimales.
Énfasis: resolver problemas de divisiones de números naturales entre decimales e identificar divisiones equivalentes (que permiten obtener el mismo resultado).
¿Qué vamos a aprender?
En esta sesión aprenderás cómo se pueden resolver divisiones de números naturales entre decimales, y buscarás la manera de ayudarlos a resolver sus dudas y dificultades.
¿Qué hacemos?
Para iniciar analiza la primera situación y observa la siguiente imagen:

En la imagen se muestra una familia integrada por cuatro operaciones. Se trata de divisiones entre números naturales; pareciera que son sencillas de resolver, pero el grado de dificultad en esta ocasión no es el propósito a seguir, sino que las tienes que resolver, analiza e identifica la relación que se establece entre el dividiendo, el divisor y el cociente entre las 4 operaciones.
- Ocho entre cuatro es igual a dos.
- 16 entre ocho es igual a dos.
- 72 entre 36 es igual a dos.
- 360 entre 180 es igual a dos.
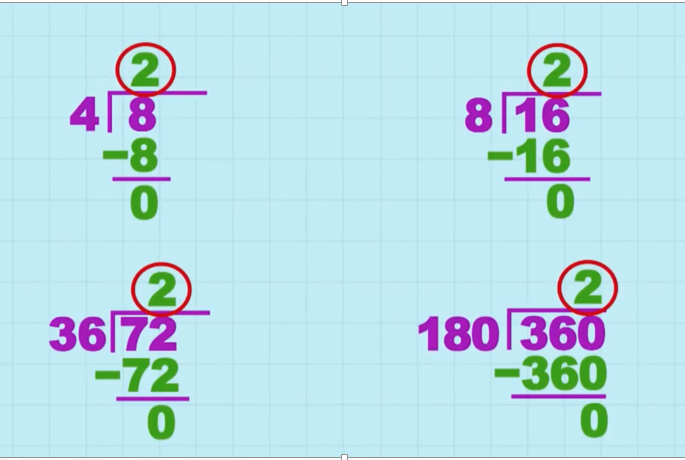
¿Qué relación identificaste entre el dividendo y el divisor de la familia de operaciones? ¿Por qué en todas las divisiones el cociente es igual a 2?
Analiza el primer par de divisiones.
Ocho entre cuatro es igual a dos.
16 entre ocho es igual a dos.
En la primera división, el dividendo es 8 y el divisor es 4. En la segunda división, el dividendo es 16 y el divisor es 8.
El dividendo de la segunda división es el doble del dividendo de la primera división: 16 es el doble de 8; así como el divisor de la segunda división es doble del divisor de la primera división: 8 es el doble de 4.
O mejor aún, el dividendo y el divisor de la operación 1 se multiplican por 2 para obtener el dividendo y el divisor de la operación 2.
- 4 por 2 = 8
- 8 por 2 = 16
Es decir, hay una relación multiplicativa entre los elementos de la división, ¿es por esta relación que el cociente es el mismo?, ¿las dos operaciones son equivalentes?, ¿qué significa esto último?, ¿esta relación multiplicativa aplica a cualquier tipo de división?, ¿en qué condiciones?
Para construir argumentos que te ayuden a responder las preguntas anteriores, aplica la relación multiplicativa entre los elementos de la división:
Sea la primera división 7 entre 4, es decir, el dividendo 7 y el divisor 4. En una nueva división, para que el cociente sea el mismo que en la división 1, ¿qué valores deben tener el dividendo y el divisor?
Multiplica el dividendo 7 y el divisor 4.
- 7 por 2 = 14
- 4 por 2 = 8
Al resolver las divisiones, tienes que:
- 7 entre 4 es igual a 1.75
- 14 entre 8 es igual a 1.75
Los cocientes son iguales.
Para este par de divisiones, la relación multiplicativa sí funciona. Ahora sólo has multiplicado por 2, ¿sucederá lo mismo si se emplea un factor distinto a 2?
Por ejemplo, 1.5
Multiplica el dividendo 7 y el divisor 4 por 1.5:
- 7 por 1.5 = 10.5
- 4 por 1.5 = 6
Resuelve las divisiones:
- 7 entre 4 es igual a 1.75
- 10.5 entre 6 es igual a 1.75
Los cocientes son iguales.
Replantea las preguntas anteriores para construir un sentido y significado sobre divisiones equivalentes.
¿Qué relación identificaste entre el dividendo y el divisor de la familia de operaciones? ¿Cuándo dos o más operaciones son equivalentes?
Has analizado algunos casos particulares donde las divisiones tienen el mismo cociente o resultado. En estos casos particulares identificaste que hay una relación multiplicativa entre el dividendo y el divisor de las operaciones involucradas. Es decir, dada una división, sus elementos se multiplican por el mismo factor. Si esta condición no se cumple, las divisiones no son equivalentes.
Para formalizar lo analizado, analiza la información del siguiente video que explica cómo obtener divisiones equivalentes.
- Divisiones con el mismo resultado.
https://www.youtube.com/watch?v=y74aYkN5H-Q
De acuerdo con la información del video, aprendiste cómo obtener divisiones equivalentes multiplicando por un mismo número tanto el dividendo como el divisor. Esta propiedad de las divisiones te será de ayuda para resolver divisiones con números decimales y números enteros.
Observa la siguiente problemática.
“En el libro de Matemáticas, Joshua se encontró con la siguiente división: 660 entre 5.5. Inmediatamente le preguntó a su hermana Ruty cómo podrían resolverla, y si habrá otras divisiones equivalentes a ella.”
¿Qué piensas?, ¿cómo resolverías la división?
Al igual que Joshua, al revisar tus libros de Matemáticas, puedes encontrarte con divisiones con diferentes tipos de números. Una manera de enfrentar esta situación es analizar la operación y caracterizar los números que están involucrados:
660 es un número natural del orden de las centenas.
5.5 es un número decimal. La parte decimal es del orden de los décimos.
Conforme a lo anterior, aritméticamente se plantea la división de un número natural entre un número decimal.
Para ello, se multiplica tanto el divisor como el dividendo por la misma potencia de diez, según el número de cifras decimales que tenga el número decimal. En este caso, en el dividendo sólo se tiene una cifra decimal, por lo que ambos números se multiplican por 10:
- 5.5 x 10 = 55
- 660 x 10 = 6 600
Así obtienes la división de números naturales: 6 600 entre 55.
Esta es una división equivalente a 660 entre 5.5.
Ya tienes dos números naturales: 55 y 6 600, por lo que se puede resolver la división de números naturales que ya conoces.
Seguramente conoces este procedimiento de división entre dos números naturales, y quizás tengas algunos conocimientos con respecto de algunos pasos, pues para resolver los algoritmos puedes realizar una serie de pasos, ya que se trata de un método y, como todo método, implica un orden.
Esto no significa que tengas que memorizarlo, sino que comprendas en qué consiste cada uno de estos pasos, y una vez que lo comprendas, utilizarlo en la resolución de problemas aritméticos. De esta manera, favoreces tu pensamiento matemático o abstracto.
Ahora establece más de una división equivalente a 660 entre 5.5.
“Joshua propuso la división 132 entre 11, y Ruty, 264 entre 2.2.”
Resuelve, analiza e identifica la relación que se establece entre el dividiendo, el divisor y el cociente, entre las divisiones propuestas y la original.
“Ruty le pidió a Joshua que argumentara su postura, explicando por qué la división 132 entre 11 es equivalente a 660 entre 5.5.”
El argumento de Joshua es el siguiente:
“Dada la relación multiplicativa que se establece entre el divisor y el dividendo, para generar otra operación equivalente, se multiplica 660 por 0.2, que es igual a 132, y 5.5 por 0.2, que es igual a 1.1. Los resultados obtenidos en cada caso permitieron establecer la operación equivalente: 132 entre 11, cuyo cociente es 120. Esto comprueba que las operaciones 660 entre 5.5 y 132 entre 1.1 sí son equivalentes.”
Joshua aplicó lo que él aprendió sobre las relaciones entre los elementos de una división. Ahora considera el argumento de Ruty.
Ella explicó:
“Yo también me basé en la relación multiplicativa que se establece entre el divisor y el dividendo, pero, para generar otra operación equivalente, dividí 660 entre 2.5, que es igual a 264, y 5.5 entre 2.5, que es igual a 2.2. Los resultados obtenidos en cada caso me permitieron establecer también una operación equivalente: 264 entre 2.2, cuyo cociente es 120. Esto comprueba que las operaciones 660 entre 5.5, 132 entre 11 y 264 entre 2.2 sí son equivalentes.”
Ella fue más allá de lo que se vio en la sesión, pues sabes que la relación multiplicativa identificada antes no sólo refiere a realizar multiplicaciones, sino también divisiones, pues entre estas operaciones existe una relación inversa.
Para profundizar en el tema, aplica el razonamiento de Ruty para determinar la o las operaciones equivalentes a las siguientes divisiones.
Sea la división 180 entre 4.5 igual a 40.
Analiza las divisiones 15 entre 0.375 y 360 entre 9 con la finalidad de determinar si son o no equivalentes a 180 entre 4.5.
Observa el primer caso.
Para obtener 15, se dividió 180 entre 12.
Para obtener 0.375, se dividió 4.5 entre 12.
Al dividir 15 entre 0.375, el cociente es 40.
De esta manera, se puede afirmar que las operaciones 180 entre 4.5 y 15 entre 0.375 son equivalentes.
El segundo caso:
Para obtener 360, se dividió 180 entre 0.5.
Para obtener 9, se dividió 4.5 entre 0.5.
Al dividir 360 entre 9, el cociente es 40.
De esta manera, se afirma que las operaciones 180 entre 4.5, 15 entre 0.375 y 360 entre 9 son equivalentes.
Se han propuesto operaciones para resaltar las relaciones multiplicativas entre ellas y construir un significado sobre las divisiones equivalentes cuando se divide un número natural entre un número decimal.
Ahora resuelve la siguiente situación y analiza cómo se puede aplicar la propiedad de la división vista anteriormente y el algoritmo de la misma en la solución del problema.
“Eduardo, el carpintero del pueblo, necesita construir las puertas de un ropero con madera. Si compró siete y medio metros cuadrados de madera y pagó en total la cantidad de $1 350.”
¿Cuál es el precio por metro cuadrado de madera?
Analizando la situación, observa que el costo de los 7.5 metros cuadrados de madera fue de 1 350 pesos, y se solicita encontrar el precio por metro cuadrado de madera.
¿Qué operación ayuda a determinar el costo solicitado en el planteamiento?
Caracteriza los números 1350 es un número natural, de orden de unidades de millar. 7.5 es un número decimal. La parte decimal es del orden de los décimos.
Conforme a lo anterior, aritméticamente se plantea la división de un número natural entre un número decimal. Sabes que la manera de resolver la división de números naturales entre decimales es convertir el divisor en un número natural.
Para ello, se multiplica tanto el divisor como el dividendo por la misma potencia de diez, según el número de cifras decimales que tenga el número decimal del dividendo. En este caso, sólo se tiene 1, por lo que ambos números se multiplican por 10.
- 7.5 x 10 = 75
- 1 350 x 10 = 13 500
Ya tienes en este caso una división de números naturales: 13 500 entre 75; al resolverla, el cociente es 180.
En el contexto del planteamiento, 180 representa el costo del metro cuadrado de madera.
Con estos ejemplos se te apoya en lograr un aprendizaje con sentido y significado. Ahora se te invita a resolver un último problema.
“Se tiene un cuadrado cuyo perímetro es de 27.9 metros.” ¿Cuál es la medida de sus lados?
Caracterizando los números involucrados en el planteamiento: 27.9 es un número decimal. La parte decimal es del orden de los décimos. Y sabes que todo cuadrado tiene 4 lados iguales. Para responder la pregunta: ¿cuál es la medida de los lados?, se divide un número decimal entre un número natural.
Para dar respuesta a la pregunta anterior, hay varios caminos que pueden ser de utilidad para dar sentido y significado a las divisiones con números decimales, donde se divide un número decimal entre un número natural.
Uno de ellos es realizar una estimación razonable, es decir, pensar qué número multiplicado por 4, ya que todo cuadrado tiene todos sus lados iguales, se acerca a 28.
7 por 4 es igual a 28, por lo tanto, la medida aproximada de los lados del cuadrado es de 7 m.
Otro camino es convertir al número 27.9 a número natural. Para ello, se multiplica tanto el divisor como el dividendo por la misma potencia de diez, según el número de cifras decimales que tenga el número decimal. En este caso, sólo se tiene 1, por lo que ambos números se multiplican por 10:
- 27.9 x 10 = 279
- 4 x 10 = 40
De esta manera, al dividir 279 entre 40, el cociente es igual a 6.975, número que representa la medida en metros de cada uno de los lados del cuadrado.
Al comparar los resultados, se identifica que 7 es una buena estimación en medida, pues cada lado mide 6.975 metros. Esto significa que desarrollar tu sentido numérico respecto a las operaciones se convierte en una fortaleza para dar respuesta a situaciones desconocidas o difíciles.
Has llegado al final de la sesión.
El reto del hoy:
Para complementar lo estudiado puedes consultar otras fuentes, como tu libro de texto de Matemáticas de primer grado, o puedes recurrir a tu profesora o profesor de esta asignatura.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas