Distintas ecuaciones para un mismo problema

Distintas ecuaciones para un mismo problema

Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de ecuaciones lineales.

Énfasis: identificar y resolver diferentes ecuaciones que pueden representar a un mismo problema.

¿Qué vamos a aprender?

En esta sesión trabajarás con problemas que se pueden resolver con más de una ecuación lineal, a través del planteamiento de situaciones en diversos contextos.

Se te recomienda tener a la mano tu cuaderno, o en su defecto, hojas reutilizables, lápiz, goma y regla, Así como tu libro de texto.

¿Qué hacemos?

Para iniciar, analiza la siguiente situación-problema y reflexiona sobre los puntos importantes que se vayan mencionando.

Si la suma de dos números es 180 y uno es el triple del otro, ¿cuáles son esos números?

Para dar respuesta a la pregunta, lo primero que debes hacer es traducir la situación a lenguaje algebraico para, posteriormente, dar respuesta a la situación planteada.

En este caso, tienes el primer número, que se representará con la literal “x”.

El triple de ese número lo escribes como: 3x.

Ahora, representas el enunciado “la suma de los dos números es igual a 180”, lo escribes algebraicamente como la ecuación lineal: x + 3x = 180.

Ya tienes la ecuación que modela la situación; es momento de resolverla respetando las propiedades y las reglas de la igualdad que ya conoces.

Primero, debes simplificar los términos semejantes en el primer miembro de la ecuación: x + 3x es igual a 4x; así, tienes la ecuación equivalente 4x = 180. Para despejar a “x” divides ambos miembros entre 4, dando 4x/4 = 180/4. Resolviendo las operaciones, obtienes el valor de “x” que es igual a 45.

Ahora sí, ya tienes elementos suficientes para poder responder la pregunta y solucionar la situación. La suma de dos números es 180 y uno es el triple del otro, ¿cuáles son esos números?

Como “x” es el primer número, de acuerdo con la representación algebraica, tienes que x = 45, que es el primer número.

Como el triple del número es 3x y “x” vale 45, tienes que 3 por 45 es igual a 135, que es el segundo número.

Hay que hacer la comprobación, sustituyendo el valor de “x” en la expresión que modela la situación trabajada: x + 3x = 180.

Al sustituir el valor de “x”, se tiene que:

45 + 3 (45) = 180

45 + 135 = 180

180 = 180

La igualdad entre ambos miembros indica que el resultado obtenido para “x” es correcto. De esta forma, queda comprobado que la respuesta es correcta.

Se ha resuelto satisfactoriamente la situación planteada, pero ¿será la única ecuación lineal que se puede plantear, a partir de la situación-problema?

Piénsalo un momento.

En algunas situaciones se puede plantear más de una ecuación, la cual puede modelar el problema y que, al ser resuelta, se encuentren los mismos resultados. Observa.

En la situación anterior se puede considerar que el primer número es el triple del segundo, el cual se representa con la letra “a”; entonces, se puede representar al segundo número con la expresión a/3, es decir, un tercio de “a”. Así, la condición no cambia, puesto que queda entendido que un número es el triple del otro; o bien, el segundo número es un tercio del primero, es decir, a/3 + a = 180.

Ya se tiene la nueva ecuación que representa el mismo problema. Revisa lo que sucede. No olvides tomar nota de lo que consideres importante y escribir las dudas que vayan surgiendo durante el proceso.

Primero, se reducen los términos semejantes del primer miembro, así que se procede a sumar: a + a/3, lo puedes escribir como 1/3”a” + 3/3”a” = 4/3”a”; así tienes que: 4/3”a” = 180.

Para despejar la incógnita, como 4/3 está multiplicando a “a”, se puede dividir ambos términos entre 4/3, quedando 4/3”a” entre 4/3 = 180/4/3.

Al resolver las operaciones, 4/3”a” entre 4/3 es igual a “a”; y, por otro lado, 180 entre 4/3 es igual a 540/4 a su vez igual a 135. Con esto se tiene que a = 135.

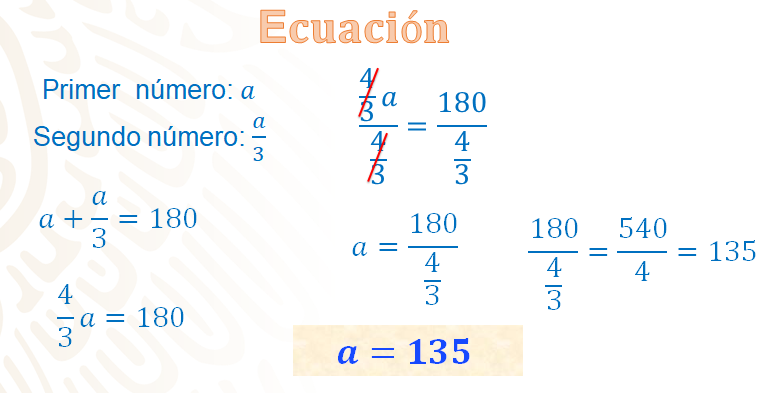
Ahora, relaciona los valores obtenidos con la incógnita “a” para comprobar la respuesta. Esto es a = 135, que es el primer número; y, para obtener el segundo número, utiliza la expresión a/3; sustituyendo “a”, resulta que 135/3 = 45, que es el valor del segundo número.

Comprobando el valor obtenido de “a” en la ecuación, se ve que cumple con la igualdad. Para comprobar la respuesta, se sustituye el valor de “a”, y tienes que 135 + 135/3 = 180; al resolver 135/3 = 45 y, si sumas 135 + 45 = 180; y 180 es igual a 180, lo cual indica que la solución de la ecuación es correcta.

Se ha logrado trabajar con dos ecuaciones diferentes para resolver una misma situación.

A continuación, analiza y resuelve la siguiente actividad.

Vicente compró dos camisas y un pantalón, por los que pagó 350 pesos. Aunque desconoce el precio de cada prenda, sabe que el precio de cada pantalón es 50 pesos más que el de una camisa.

¿Cuál es el precio de cada prenda?

Considera que, para resolver el problema, es necesario traducir a lenguaje algebraico la situación–problema, como se muestra a continuación.

Se representa el precio de la camisa con la literal “c” y el del pantalón con la literal “p”.

Como el precio del pantalón es 50 pesos más que el de una camisa, puedes expresarlo algebraicamente como: p = c + 50.

La situación está determinada por la siguiente relación: el precio de 2 camisas + un pantalón = 350 pesos, esto es 2c + p = 350.

Tienes dos ecuaciones y dos literales, entonces para trabajar con una sola ecuación y una sola literal debes realizar lo siguiente:

Como el precio del pantalón “p” algebraicamente es igual a “c + 50”; entonces, en la expresión 2c + p = 350, sustituye “p” por “c + 50” y te queda la ecuación: 2c + c + 50 = 350.

Ahora ya tienes la ecuación con una incógnita, la cual vas a resolver aplicando las propiedades de la igualdad.

Tienes que: 2c + c + 50 = 350. Primero, reduces términos semejantes del lado izquierdo de la igualdad, obteniendo la ecuación 3c + 50 = 350.

Posteriormente, restas 50 en ambos miembros de la igualdad, quedando: 3c + 50 – 50 = 350 – 50 y, al simplificar, queda: 3c = 300.

Por último, tienes a 3 que multiplica a “c”; así que procedes a dividir ambos miembros entre 3, para que no se altere la igualdad, quedando: 3c/3 = 300/3. Al resolver las operaciones, resulta que c = 100; es decir, el precio de cada camisa es de $100.

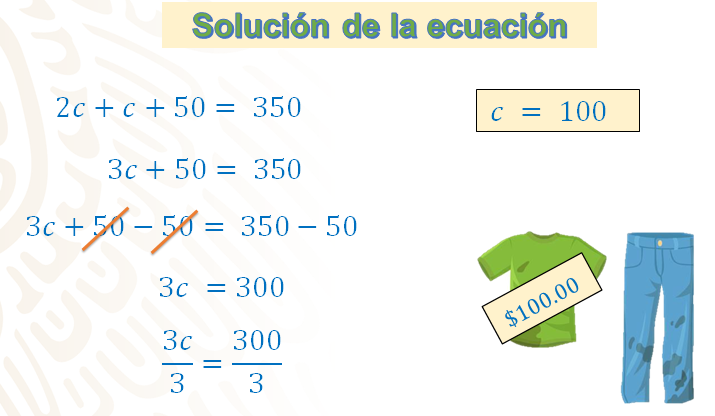
Con este resultado ya se puede calcular el precio del pantalón, resuélvelo algebraicamente.

Sustituye el valor de “c” en la expresión: 2c + p = 350, para obtener el precio del pantalón; es decir, el valor de “p”. Al sustituir “c”, tienes: 2 por 100 más p es igual a 350. Resuelve la multiplicación 2 por 100 y queda la ecuación: 200 + p = 350.

Para despejar “p”, observa que se está sumando con 200; así que resta 200 en ambos miembros de la ecuación, para que la igualdad se mantenga y tienes: 200 + p – 200 = 350 – 200. Al simplificar la ecuación, obtienes: p = 150; es decir, el precio del pantalón es de 150 pesos.

Con lo anterior ya se dio respuesta a la pregunta: ¿cuánto vale cada prenda de vestir?

Para comprobar los resultados, suma el precio de las prendas: 2 por 100 más 150 es igual a 200 más 150, igual a 350, que es la cantidad que pagó Vicente por las tres prendas.

Con el fin de ir consolidando lo que has realizado al resolver los problemas anteriores, en los que el uso de ecuaciones lineales ha sido importante, analiza la siguiente situación y resuélvela.

Sonia fue a la papelería para comprar 5 cuadernos y 3 bolígrafos por los que pagó 301 pesos. Se sabe que el precio de un cuaderno es igual al precio de ocho bolígrafos; es decir, ocho veces mayor.

¿Cuál es el precio de cada cuaderno y de cada bolígrafo?

Si asignas la literal “c” al precio de los cuadernos y la “b” al de los bolígrafos, ¿cuál sería la expresión algebraica que modela el problema? Escríbela en tu cuaderno.

Revisa si lo que escribiste es parecido a lo siguiente: 5c + 3b = 301.

Esta expresión algebraica servirá de base para encontrar los precios de los artículos. De la lectura del problema, se sabe que el precio de un cuaderno es ocho veces el precio de un bolígrafo. ¿Cómo se representa algebraicamente esto?

Intenta hacerlo.

La expresión algebraica es: c = 8b.

Si en la expresión algebraica 5c + 3b = 301, sustituyes a “c” por “8b”, obtienes una ecuación con una sola incógnita y queda lo siguiente: 5 por 8b + 3b = 301.

Observa que 5 multiplica a 8b; al resolver, el producto es 40b, por lo que queda la ecuación: 40b + 3b = 301. Ahora se deben agrupar términos semejantes para simplificar la ecuación: 40b + 3b = 43b; así, queda la ecuación: 43b = 301.

Para despejar a “b” divides ambos miembros de la ecuación entre 43; de donde resulta: 43b/43 = 301/43.

Al realizar las divisiones te queda que b = 7.

Esto quiere decir que cada bolígrafo tiene un precio de 7 pesos.

Al sustituir el valor de “b” en la expresión c = 8b, obtienes el precio de cada cuaderno. Realízalo.

c = 8 por (7), de donde resulta que c = 56; esto es que cada cuaderno tiene un precio de 56 pesos.

Hay que comprobar estos valores en la ecuación inicial: 5c + 3b = 301.

Al sustituir los valores encontrados obtienes:

5(56) + 3(7) = 301. Realizando las operaciones, 5 por 56 y 3 por 7 queda, 280 + 21 = 301. Tras realizar la suma del primer miembro, resulta que 301 = 301, con lo que queda comprobado que esos valores son el precio de cada cuaderno y de cada bolígrafo.

¿Habrá otra manera de resolver este problema?

La respuesta es sí.

Otra forma de resolverlo es a partir de relacionar, de otra manera, el precio de cada cuaderno con el de cada bolígrafo.

De los datos que se proporcionan en el problema, se tiene que cada cuaderno vale ocho veces el precio de un bolígrafo. Ya viste que la expresión que los relaciona es: c = 8b y de ella puedes obtener que el precio de cada bolígrafo es la octava parte del de un cuaderno, esto es: b = c/8.

Si sustituyes esta expresión en la ecuación de base, se tiene que: 5c + 3(c/8) = 301.

Observa que en el primer miembro se tiene una suma de fracciones y, para realizarla, es necesario obtener fracciones que tengan denominador común. Expresa a 5 enteros en octavos que es igual a 40/8, por lo que queda: 40/8 c + 3/8 c = 301.

Al realizar la suma de cuarenta octavos más tres octavos, se obtiene que: 43/8 c = 301.

Despeja “c” para obtener su valor; para hacerlo aplica la propiedad uniforme de la igualdad, que indica que lo que se haga en un miembro de la ecuación, tiene que hacerse en el otro. Divide ambos miembros de la ecuación entre 43/8:

43/8 c entre 43/8 es igual a 301 entre 43/8, por lo que “c” = 301 entre 43/8, de donde resulta: c = 301 por 8 entre 43, en donde “c” = 2408 entre 43. Al resolver la división, c = 56, es decir, que, efectivamente, cada cuaderno tiene un precio de 56 pesos, lo que ya se había obtenido previamente.

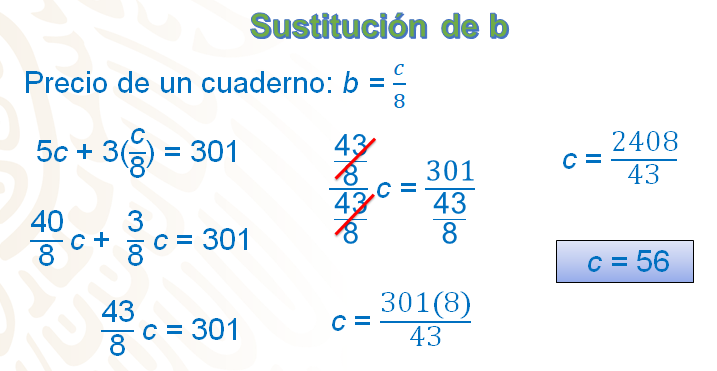
Al sustituir este valor en la expresión b = c/8, tienes que b = 56/8; es decir que b = 7, y así corroboras que el precio de cada bolígrafo es de 7 pesos.

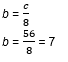
Ahora se resolverá el siguiente acertijo.

La edad de Memo es el doble de la de Luis, pero la mitad de la de Juan. Si las tres edades suman 77 años, ¿cuál es la edad de cada uno?

Hay que recabar la información que proporciona el problema y plantear las expresiones algebraicas y la ecuación que permitirá resolver la situación.

Se tomará la edad de Memo como la incógnita y se le asigna la literal “x”. Como la edad de Memo es el doble de la de Luis, entonces la edad de Luis es la mitad de la edad de Memo, quedando la expresión: edad de Luis x/2.

Ahora, hay que representar la edad de Juan. Como la edad de Memo es la mitad de la de Juan, se puede decir, entonces, que la edad de Juan es el doble de la edad de Memo, quedando la expresión: edad de Juan 2x.

Enseguida, hay que relacionar las expresiones para plantear la ecuación lineal; así, tienes que la suma de las tres edades es igual a 77, es decir, x + x/2 + 2x = 77, que es la ecuación que modela la situación.

Ahora, hay que resolverla. Pon mucha atención y no olvides hacer tus anotaciones.

Observa que, en el primer miembro, todos los términos son semejantes, ya que todos tienen la misma literal con el mismo exponente; entonces, puedes simplificarlos sumando los coeficientes: 1 + 1/2 + 2 = 3 un medio = 7/2, así obtienes la ecuación: 7/2x = 77.

Para despejar “x”, observa que 7/2 está multiplicando a “x”, así que procede a dividir tanto el primer miembro como el segundo por 7/2, quedando la expresión: 7/2x entre 7/2 = 77 entre 7/2.

Al resolver las operaciones, te queda que 7/2x entre 7/2 = x, y 77 enteros entre 7/2 = 154/7 = 22; así, se tiene que la solución de la ecuación es: x = 22.

Ahora sí, con este resultado, estas en condiciones de determinar las edades de cada persona.

La edad de Memo, “x”, es igual a 22 años; como la edad de Luis, es la mitad de la edad de Memo; es decir, x/2, que es igual a 22 entre 2, igual a 11 años. Y la edad de Juan es del doble de la edad de Memo, es decir, 2x, que es igual a 22 por 2 igual a 44 años.

Pero ¿ésta será la única manera de plantear la ecuación que resuelve el problema?

En este caso, al igual que en otros similares, se puede obtener una ecuación distinta para resolver la situación.

Estudia otra ecuación que te permita resolverla, considerando la edad de otra de las personas como la incógnita. Reflexiona, si consideras la edad de Juan como la incógnita, ¿qué ecuación permitiría resolver el problema?

Observa que sucede.

Hay que desarrollar las expresiones, pero ahora considerando a Juan como la incógnita; tienes las expresiones para cada uno de los personajes de la siguiente manera:

La edad de Juan es igual a “j”. Como Memo tiene la mitad de la edad de Juan, queda como ½ de “j” y, como Memo tiene el doble de la edad de Luis, ½ de “j” es el doble de ¼ de “j”, que es la edad de Luis. Ahora ya puedes representar la ecuación (la suma de las edades es igual a 77), quedando de la siguiente manera: j + ½ j + ¼ j = 77.

Para resolver la ecuación sigues el mismo procedimiento que en el caso anterior. Como en el primer miembro todos son términos semejantes, los sumas como fracciones equivalentes en cuartos, y para simplificar la ecuación obtienes 7/4 de “j” = 77.

En esta ocasión, vas a operar con números decimales; por ello, 7/4 lo conviertes en su representación como número decimal y tienes que 7/4 de “j” es igual a 1.75” j”.

Para despejar “j” debes dividir entre 1.75 a ambos miembros de la ecuación, quedando: 1.75j entre 1.75 igual a 77 entre 1.75. Al resolver las operaciones, tienes que 1.75j entre 1.75 es igual a “j” y 77 entre 1.75 es igual a 44; es decir, j = 44.

Esto indica que la edad de Juan es de 44 años.

Con esto se puede obtener las edades de Memo y Luis, que son: para Memo la mitad de la edad de Juan; es decir, j/2, que es igual a 44 entre 2, igual a 22 años; y para Luis se tiene que su edad es igual a ¼ de j, que es igual a 44 entre 4, igual a 11 años.

Así, se comprueba que esta nueva ecuación te permitió obtener los mismos resultados, por lo que ambas representaciones de la situación son correctas.

El reto de hoy:

El reto de hoy consiste en lo siguiente:

Retoma del último ejercicio del acertijo de las edades, como resolverías las siguientes preguntas:

• ¿Qué sucedería si la edad de Luis representa la incógnita del problema y usas la literal ele?
• ¿Cuáles serían las expresiones que representarían las edades de Memo y Juan?

Se te invita a que encuentres las edades de estos tres personajes usando una nueva ecuación.

Comparte tus resultados con tu maestra o maestro de esta asignatura, a la distancia para recibir retroalimentación.

Asimismo, revisa en tu libro de texto el tema que estudiaste en esta sesión y realiza las actividades que ahí se te sugieren.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html