¿Cuándo es posible y cuándo no?
¿Cuándo es posible y cuándo no?
Aprendizaje esperado: realiza experimentos aleatorios y registra los resultados para un acercamiento a la probabilidad frecuencial.
Énfasis: utilizar el experimento como una forma de recolección de datos y considerar cuando un evento es posible o no.
¿Qué vamos a aprender?
Utilizarás el experimento como una forma de recolección de datos y considerarás cuándo un evento es posible o no.
¿Qué hacemos?
En la vida diaria puedes realizar experimentos que se pueden clasificar como deterministas y aleatorios.
Los experimentos deterministas son llamados así porque su resultado se sabe con certeza antes de realizarlos; un ejemplo de ellos es cuando se pone un recipiente con agua al fuego, sabes de antemano que el agua se calentará.
Los experimentos aleatorios son aquellos donde su resultado no se sabe o se desconoce; es decir, por muchas veces que los repitas en igualdad de condiciones, no conocerás el resultado, un ejemplo son los juegos de azar.
Conforme a esta clasificación revisarás ejercicios en donde identifiques experimentos deterministas o aleatorios.
El primero, consiste en tirar a una portería y anotar un gol es un evento aleatorio porque no puedes saber si anotarás un gol.
Calcular el perímetro de un cuadrado conociendo la medida de su lado, es un experimento determinista; ya que, si tienes el conocimiento de la fórmula y realizas correctamente las operaciones, se garantiza que obtendrás el perímetro del cuadrado.
Saber en qué ciudad vives, es determinista; ya que se comprueba en el domicilio físico.
Se dice que un dado está cargado cuando existe un peso desigual hacia una cara del dado, favoreciendo que ésta salga más veces. Lanzar un dado y que salga el número 6 es un experimento aleatorio ya que, si no está cargado hacia un número específico, no se puede asegurar qué número saldrá.
Girar una ruleta dividida en partes iguales y determinar en qué zona se detendrá es también un experimento aleatorio; ya que depende de varios factores para que se detenga en un lugar específico.
Jugar a la lotería y no saber el número ganador, es un experimento aleatorio ya que hay miles de combinaciones y no puedes asegurar la combinación ganadora.
Lanzar una moneda y que caiga águila, es también un experimento aleatorio pues no sabes qué cara caerá en el lanzamiento.
Como viste se han clasificado algunos experimentos aleatorios y deterministas.
Cuando lanzas una moneda estás realizando un experimento aleatorio, donde no sabes o no hay certeza sobre qué cara de la moneda caerá hacia arriba, pues las opciones de lanzar una moneda al aire son dos, que caiga águila o sol, entonces esos resultados forman parte del espacio muestral, que es el conjunto de todos los posibles resultados de un experimento aleatorio.
El espacio muestral del evento “lanzar una moneda” será representado con la letra “M” mayúscula y los resultados los escribirás entre llaves. Se lee como: el espacio de eventos formado por los elementos águila y sol.

Cuando lanzas la moneda existe la posibilidad de que caiga águila, a eso se le llamará evento, o suceso, y se representará de la siguiente manera.

El evento se puede representar con cualquier letra en este caso se representará con la letra A mayúscula y se lee como: el evento A igual a caer águila.
Entonces, en este caso, también tienes un evento para cuando cae sol; porque un evento o suceso, es uno o varios de los posibles resultados del experimento aleatorio.

Como ya se mencionó, el evento lo puedes representar con cualquier letra; así que se escogió en este caso, la letra S mayúscula, y se lee como: el evento S igual a caer sol.
Realiza el experimento aleatorio desde casa. Lanza una moneda al aire y, al caer, registra la cara que quedó hacia arriba.
- ¿Cayó sol o águila?
- ¿Qué evento piensas que tenga mayor probabilidad, que caigan más caras de sol o más caras de águila?
Esta última pregunta hace referencia al concepto de probabilidad, que es el grado de certidumbre con que se mide la ocurrencia de cierto resultado.
El experimento que estás desarrollando se conoce como probabilidad frecuencial o empírica; y es la que se fundamenta en los datos obtenidos por observación, encuestas o por una serie larga de repeticiones de un experimento, en este caso, el lanzamiento de una moneda.
Haciendo un intento por responder a la pregunta de si cayó sol o águila, si una moneda tiene dos caras tienes la mitad de las posibilidades; compruébalo realizando el experimento mediante un programa de geometría dinámica.
¿Cómo es esto?
Simularás los primeros 10 volados y registrarás los resultados de los volados que realizarás.
Por ejemplo, se simulan los primeros 10 volados. Se lanza el primer volado colocando el número 1 dentro de la casilla y se tiene sol, se simula el segundo lanzamiento colocando el número 2 dentro de la casilla, cayó sol nuevamente; para el tercer volado cayó águila, para el cuarto cayó águila, para el quinto cayó águila, para el sexto cayó nuevamente águila, para el séptimo cayó sol, para el octavo cayó águila, para el noveno cayó águila, y el décimo cayó águila.
- “Simulación de un volado”.
Observa hasta el minuto 00:58
Después compararás los registros sobre los resultados de los 10 volados anteriores, por medio de una tabla.
Para ello elaborarás una tabla con la siguiente información:
- En la primera columna registrarás el total de lanzamientos, que en este caso son 10.
- En la segunda columna, el número de veces que cayó águila, que fueron 7.
- En la tercera columna, la probabilidad frecuencial respecto a la cara “águila”, que se calcula dividiendo el número de veces que cayó —que fueron 7— entre el número de lanzamientos —que fueron 10—,lo que equivale a 0.7.
- En la cuarta columna está el número de veces que cayó sol, que fueron 3.
- En la quinta columna la probabilidad frecuencial respecto a la cara” sol”, que se calcula dividiendo el número de veces que cayó, en este caso fueron 3 entre el número de lanzamientos que fueron 10, lo que equivale a 0.3.
- La suma de las dos probabilidades es uno, que se encuentra en la sexta columna.
- 1. Tabla de registro de una moneda. Del minuto 7:35 al 9:05
https://www.youtube.com/watch?v=XmBRcq9qGZA
La probabilidad frecuencial se determina cuando se registran los datos y se divide el número de veces que se obtiene el resultado que te interesa, entre el número de veces que se realizó el experimento.
La probabilidad frecuencial es igual al número de eventos favorables entre el número total de los experimentos realizados, conforme a los primeros 10 lanzamientos de la moneda, la probabilidad frecuencial del evento A caer águila es igual a: 7 entre 10 porque cayeron 7 águilas entre 10 lanzamientos totales.

¿Qué observaste?
La probabilidad que salió en el ejemplo dado, de que salga águila en este experimento fue mayor que la de sol.
En el caso de tú experimento.
- ¿Cuál fue tu probabilidad frecuencial?
- ¿Coincidió con la del ejemplo o fue diferente?
- ¿A qué consideras que se deba?
Si se vuelve a realizar el experimento, pero ahora con 50 volados, ¿la probabilidad será la misma?
Hay que averiguarlo en el siguiente ejemplo.
Se continúo experimentando y para el lanzamiento número 20 cayó águila, para el evento número 50, cayó sol, en este momento es oportuno mencionar que han caído hasta el momento 24 veces sol y 26 veces águila.
- “Simulación de un volado”.
https://youtu.be/OfcxWqFT_sQ
Observa del minuto 00:58 al 01:26
Se compararon los registros, sobre los resultados de los 50 volados anteriores y se registraron los datos, en 50 lanzamientos, cayeron 26 “águilas”, su probabilidad frecuencial equivale a las veces que cayó —que son 26— entre 50, ya que ahora fueron 50 lanzamientos y es igual a 0.52; cayó 24 veces “sol”, su probabilidad frecuencial se calcula al dividir 24 entre 50 que es igual a 0.48, sumando las probabilidades resulta 1. - 1. Tabla de registro de una moneda. Del minuto 10:18 a 11:05
https://www.youtube.com/watch?v=XmBRcq9qGZA
Se comparó la probabilidad frecuencial de 10 y de 50 lanzamientos del evento águila, de 10 lanzamientos la probabilidad frecuencial fue de 0.7 y de 50 lanzamientos la probabilidad frecuencial fue de 0.52.
¿La probabilidad aumentó, disminuyó o fue la misma?
Antes de contestar a esta interrogante, se aumentará la cantidad a 100 lanzamientos de una moneda.
¿Será la misma probabilidad?
Atención en el siguiente audiovisual: - “Simulación de un volado”.
https://youtu.be/OfcxWqFT_sQ
Observa del minuto 01:26 al 01:49
Se procedió con el experimento, el lanzamiento número 75 cayó sol, en el momento del evento número 100 cayó águila, en 51 veces ha caído sol y 49 águila.
Se colocaron los resultados en la tabla de registro de la probabilidad frecuencial de 100 volados. - 1. Tabla de registro de una moneda. Del minuto 11:56 al 12:33
https://www.youtube.com/watch?v=XmBRcq9qGZA
Se realizó el registro para 100 lanzamientos, en los cuales cayeron 49 “águilas”; su probabilidad frecuencial se calcula 49 entre 100, lo que es igual a 0.49. Cayó 51 veces “sol”, su probabilidad frecuencial se calcula como 51 entre 100, lo que es igual a 0.51, sumando sus probabilidades es igual a 1.
¿Y si se aumentará la cantidad a 500 lanzamientos de una moneda? ¿Será la misma probabilidad? Compruébalo en el siguiente audiovisual. - “Simulación de un volado”.
https://youtu.be/OfcxWqFT_sQ
Observa del minuto 01:49 al 02:17
Para el lanzamiento número 300 cayó sol, en el evento número 500 cayó sol, esto quiere decir que se llevan 230 veces que ha caído sol y 270 veces que ha caído águila.
Se colocaron los resultados en la tabla de registro de la probabilidad frecuencial de 500 volados. - 1. Tabla de registro de una moneda. Del minuto 13:08 al 13:45
https://www.youtube.com/watch?v=XmBRcq9qGZA
Se realizó el registro para 500 lanzamientos, en donde cayeron 270 veces la cara “águila”, su probabilidad frecuencial se obtiene al dividir 270 entre 500, que es igual a 0.54. De 500 lanzamientos, en 230 cayó la cara “sol”, su probabilidad frecuencial se obtiene al dividir 230 entre 500 que es igual a 0.46, sumando las probabilidades de los dos eventos nuevamente resulta 1.
Se aumentará la cantidad a 1000 lanzamientos de una moneda. ¿Será la misma probabilidad? Revisa el audiovisual. - “Simulación de un volado”.
Observa del minuto 02:17 al 02:53
En el lanzamiento número 750 cayó sol y en el evento número 1000 cayó sol; se llevan contabilizados, hasta el momento, 470 veces que ha caído sol y 530 veces en las que ha caído águila, recuerdas que puedes continuar con el experimento tantas veces como consideres necesario.
Se colocaron los resultados en la tabla de registro de la probabilidad frecuencial de 1000 volados.
- 1. Tabla de registro de una moneda. Del minuto 14:23 al 15:05
https://www.youtube.com/watch?v=XmBRcq9qGZA
Se hizo el registro de 1000 lanzamientos en donde cayeron 530 veces la cara “águila”, su probabilidad frecuencial se calcula al dividir 530 entre 1000, que es igual a 0.53; la cara “sol” cayó 470 veces, su probabilidad frecuencial se calcula al dividir 470 entre 1000, que es igual a 0.47; sumando las probabilidades de los dos eventos iguala a 1.
Piensa en la comparación que se dio entre las probabilidades frecuenciales de los experimentos aleatorios de 10, 50, 100, 500 y 1000 eventos ¿qué observaste?
- 1. Tabla de registro de una moneda. Del minuto 15:18 al 17:00
https://www.youtube.com/watch?v=XmBRcq9qGZA
En 10 lanzamientos la probabilidad de que cayera águila es de 0.7 y la de sol es de 0.3, lo que significa que la probabilidad de que al lanzar 10 veces una moneda caiga la cara de águila es mayor que la probabilidad de que caiga la cara de sol.
Mientras que, para 50 lanzamientos, la probabilidad de que caiga la cara de águila es de 0.52 y la de sol es de 0.48, una vez más la probabilidad de que caiga águila es mayor respecto a la de sol.
Para 100 lanzamientos, la probabilidad de que salga águila es de 0.49, mientras que la de sol es de 0.51, en este caso la probabilidad de que caiga la cara de sol es mayor respecto a la medida de probabilidad de la cara de águila.
Para 500 lanzamientos la probabilidad de que caiga la cara de águila es de 0.54, mientras que la de sol es de 0.46, una vez más la probabilidad de que caiga la cara de águila es mayor que la de sol. Y para los 1000 lanzamientos, la probabilidad de que caiga la cara de águila es de 0.53 y la de sol es de 0.47, de nuevo la medida de probabilidad de que caiga la cara de águila es mayor respecto a la de sol.
Para el caso del lanzamiento de la moneda, pudiste observar que entre más experimentos realices, las probabilidades tienden a ser iguales entre caer sol o caer águila, en otras palabras: tanto el evento “caer águila” como el evento “caer sol” son cercanas al 0.5.
Ahora revisarás un ejemplo más, en donde se realizará otro experimento para continuar analizando la probabilidad frecuencial, esta vez con una ruleta.
Para representar el espacio muestral te apoyarás de la siguiente imagen:
En este caso el espacio muestral se representará con la letra “R” mayúscula y los posibles resultados estarán dentro de las llaves; éstos, los leerás como el espacio de eventos que lo forman y que son: verde, rojo, azul, amarillo, café y rosa.
Los eventos son los resultados que indica la flecha después de haber sido girada en la ruleta. No olvides concentrar los datos en una tabla. Observa, cual es el evento A “girar la ruleta y que se detenga en la sección de color rojo”.
Se calcula entonces la probabilidad frecuencial de que la ruleta se detenga en la sección de color rojo en cada uno de los diez giros. - “Simulación de una ruleta de seis colores”. Del minuto 17:37 al 18:06
https://www.youtube.com/watch?v=XmBRcq9qGZA
Para ello en el programa de geometría se cuenta con una ruleta compuesta por 6 colores, rojo, verde, rosa, café, amarillo y azul; dentro de cada sección hay 6 dígitos, los cuales se van a actualizar dependiendo de la cantidad de veces que salga cada color al momento de girar la ruleta; también se tiene 6 cuadrados que representan los que hay dentro la ruleta, esos van a representar la probabilidad frecuencial de cada color, para este caso por los primeros 10 tiros sólo se va a presentar el color rojo.
Del lado derecho se tiene una gráfica de barras, también se va a actualizar automáticamente con los giros de la ruleta y los colores que vayan surgiendo.
Se comienza girando la ruleta para los primeros 10 giros, el primero se detiene en el
color café, el segundo en azul, el tercero en rojo, el cuarto en rojo, el quinto en café, el sexto en café, el séptimo en rojo, el octavo en café, el noveno en café y el décimo giro en amarillo.
Se comparan los registros sobre los resultados de las 10 repeticiones, del experimento con la ruleta y se elabora una tabla con los resultados de los primeros 10 giros de la ruleta. - “3. Tabla de registro de la ruleta”. Del minuto 20:05 al 21:30
https://www.youtube.com/watch?v=XmBRcq9qGZA
En la primera columna encontrarás el evento color que cae, en la segunda columna el número de veces que cayó y en la tercera columna su probabilidad frecuencial.
El color azul cayó 1 vez y su probabilidad frecuencial se calcula como 1 entre 10 que es igual a 0.1; el color rojo cayó 3 veces y su probabilidad frecuencial se calcula como 3 entre 10 que es igual a 0.3; el color verde cayó 0 veces por lo tanto su probabilidad frecuencial es 0; el color rosa cayó 0 veces, por lo tanto su probabilidad frecuencial es 0; el color café cayó 5 veces, su probabilidad frecuencial se calcula como 5 entre 10 que es igual a 0.5; el color amarillo cayó 1 vez y su probabilidad frecuencial se calcula como 1 entre 10 que es igual a 0.1.
Si se suman el total de lanzamientos fueron 10 y las probabilidades frecuenciales de cada uno de los colores son igual a 1.
Nuevamente se gira la ruleta varias veces más y se calculará entonces la probabilidad frecuencial de que la ruleta se detenga en la sección de color rojo, después de haber girado la ruleta 50 veces.
Se puede continuar girando la ruleta, hasta que el número de giros llegue a la 50, ahora también ya puedes identificar los números que equivalen a la probabilidad frecuencial, de cada color, fíjate como poco a poco la gráfica de barras de la derecha cambia de manera rápida. - “Simulación de una ruleta de seis colores”. Del minuto 21:47 al 22:10
https://www.youtube.com/watch?v=XmBRcq9qGZA
Compara los registros después de haber girado la ruleta 50 veces. - “3. Tabla de registro de la ruleta”. Del minuto 22:10 al 22:43
https://www.youtube.com/watch?v=XmBRcq9qGZA
Las probabilidades frecuenciales del color rojo, para 10 giros de la ruleta cayó 3 veces, su probabilidad frecuencial se calcula como 3 entre 10, que es igual a 0.3; para 50 giros en la ruleta el color rojo cayó 11 veces, su probabilidad frecuencial se calcula como 11 entre 50 que es igual a 0.22
Y si hicieras el experimento 100 veces ¿cuál es la probabilidad frecuencial del color rojo? - “Simulación de una ruleta de seis colores”. Del minuto 22:50 al 23:04
https://www.youtube.com/watch?v=XmBRcq9qGZA
Se continuó girando la ruleta hasta llegar a la tirada número 100, observa que la gráfica de barras no deja de tener movimiento, ya que registra los eventos como van ocurriendo. - “3. Tabla de registro de la ruleta”. Del minuto 23:08 al 23:03
https://www.youtube.com/watch?v=XmBRcq9qGZA
Revisando los registros que se tienen hasta ese momento. Para 100 giros, el color rojo cayó 21 veces; por lo tanto, su probabilidad frecuencial se calcula al dividir 21 entre 100 que es igual a 0.21.
Ahora se compararán las probabilidades frecuenciales de la sección de color rojo, en los experimentos de 10, 50, y 100 eventos.
- “3. Tabla de registro de la ruleta”. Del minuto 23:43 al 24:25
https://www.youtube.com/watch?v=XmBRcq9qGZA
Se compararon las probabilidades frecuenciales solamente del color rojo en cada uno de los giros contabilizados. En 10 giros la probabilidad fue de 0.3, mientras que, en 50 giros la probabilidad del color rojo fue de 0.22 y para 100 giros su probabilidad fue de 0.21.
Al comparar las probabilidades se puede decir que de 10 giros respecto a 50 giros la probabilidad de que cayera color rojo fue mayor en 10 giros; mientras que, si se compara la probabilidad de 50 giros respecto a 100 giros, se puede decir que la probabilidad fue mayor para 50 giros. Con estas comparaciones puedes observar que entre más veces realices el ejercicio la probabilidad frecuencial cambiará para estabilizarse muy cerca de la probabilidad que tiene el evento de ocurrir o no.
Pudiste analizar en el experimento de la ruleta, que la probabilidad de que se detenga en un color es la misma para todos los colores, ya que todos tienen la misma superficie, pero también, observaste que existen variaciones cada vez que se repetía el mismo experimento. Es así cómo, al repetir aún más veces el experimento, tendrías más cercanía en el cálculo de las probabilidades.
¿Qué tan probable es que la ruleta se detenga en el color negro o en el color blanco?
Eso es un evento imposible de que suceda porque esos colores no están en la ruleta, por el contrario, un evento seguro es que caiga cualquier color que está en la ruleta.
Recapitulando:
En esta sesión has visto cómo, a través del análisis de la probabilidad de ocurrencia de eventos en los experimentos aleatorios, puedes saber qué pasará o qué no pasará; aunque no puedes garantizar la certeza de ello puedes tener una aproximación.
Otro concepto importante es que al grupo de todos los resultados posibles que se pueden obtener al realizar un experimento se le llama espacio de eventos, o espacio muestral y se representa con una letra mayúscula.
Si quieres saber más del tema revisa tu libro de texto.
El reto de hoy:
El reto de esta lección es que calcules la probabilidad frecuencial de los demás colores de la ruleta, para ello se presenta la tabla de los eventos ocurridos en cada color.
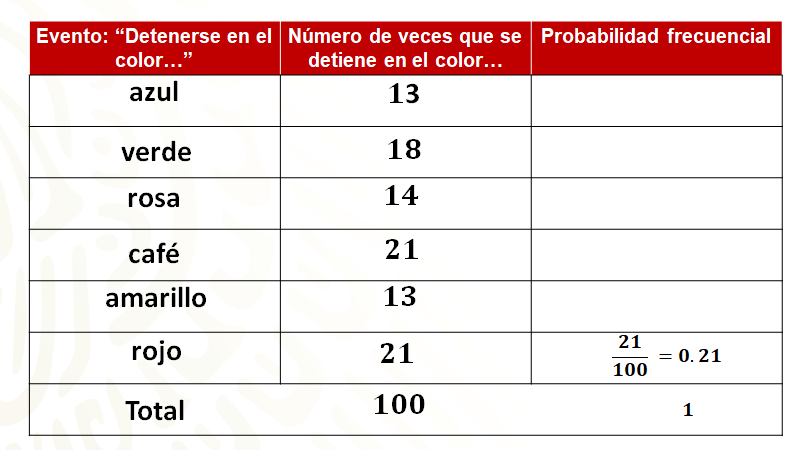
Pon atención a las columnas. En la primera los colores empiezan en azul, verde, rosa, café, amarillo y rojo, y las veces que cayó cada uno en forma respectiva fueron 13, 18, 14, 21, 13, 21, en total son 100 y la probabilidad frecuencial siempre dará 1, para el color rojo en particular fue 21 entre 100 que es equivalente a 0.21
La suma de cada una de las probabilidades siempre será uno o un número cercano a uno, dependiendo de los decimales que uses al sumar, ya que eso significa que es totalmente probable que la ruleta se detenga en cualquier color que esté en ella.
Compara tus resultados con estos.
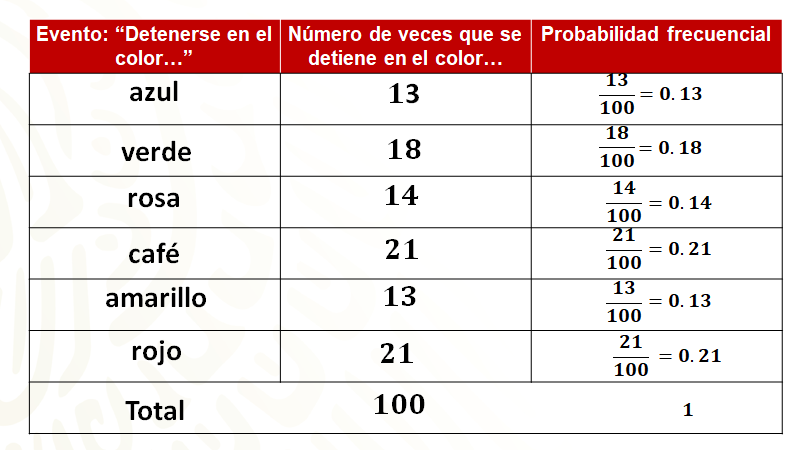
En la representación fraccionaria, la probabilidad frecuencial que se obtuvo fue la siguiente, para el color rojo 13 entre 100; el verde, 18 entre 100; para rosa, 14 entre 100; para el color café, 21 entre 100; amarillo dio 13 entre 100; y para el rojo ya sabes.
Posteriormente los resultados para cada uno fueron: en azul 0.13, en verde 0.18, para el rosa 0.14, en el café 0.21, para el amarillo 0.13 y en el rojo ya se dio a conocer.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas