Convertir fracciones a números decimales

Convertir fracciones a números decimales

Aprendizaje esperado: Convierte fracciones decimales a notación decimal y viceversa. Aproxima algunas fracciones no decimales usando la notación decimal. Ordena fracciones y números decimales.

Énfasis: convertir fracciones a números decimales.

¿Qué vamos a aprender?

En la vida diaria nos rodean situaciones que requieren el uso de fracciones. Una de esas situaciones se ve reflejada en la cocina: en las recetas de cocina casi siempre usan fracciones. El día de hoy elaborarás un panqué y verás la importancia y el uso de las fracciones, pero sobre todo de la idea de equivalencia entre dos tipos de representaciones numéricas. Resolverás estos problemas de conversión de fracciones a números decimales, mientras cocinas.

Para explorar sobre este tema, te recomendamos también consultar el Cuaderno de Trabajo del estudiante “Vamos de regreso a clases”:

https://educacionbasica.sep.gob.mx/multimedia/RSC/BASICA/Documento/202008/202008-RSC-bqXp3VgT0E-1.odesecundariaEstudianteVF.pdf

¿Qué hacemos?

Prepararás un panqué de nuez. Y para eso antes tendrás que ir a comprar los ingredientes para elaborarlo, esta es la nota de compra.

Las fracciones y los números decimales se usan y aplican en muchas actividades que realizas, y a veces no te das cuenta.

Empecemos a cocinar nuestro panqué, observemos la receta para saber los ingredientes. Algunos están en números fraccionarios y otros en números decimales, por lo que su representación es distinta, pero refieren al mismo valor. Conoceremos el procedimiento que nos permita identificarlo.

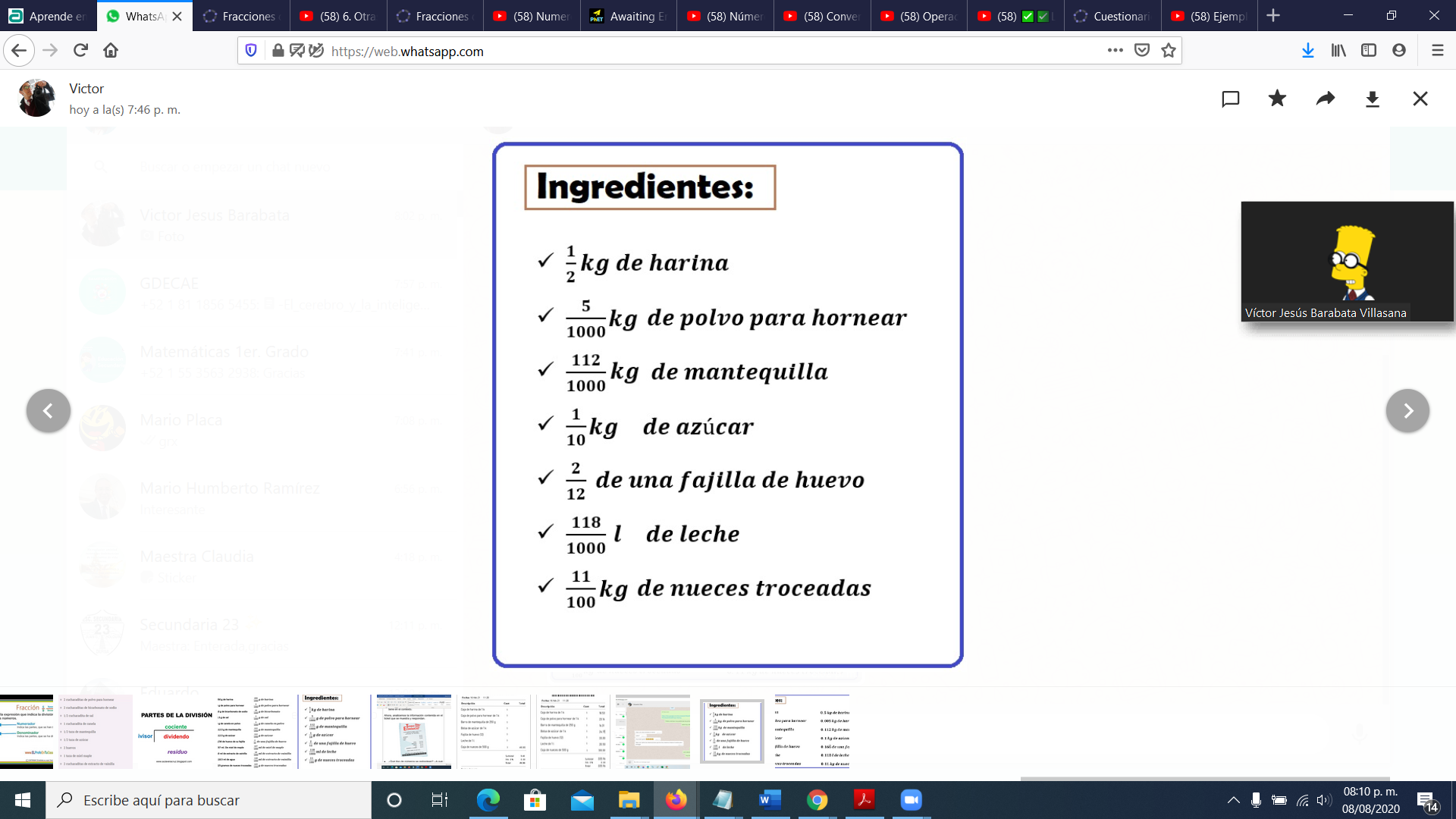
En esta ocasión vamos a convertir las medidas de los ingredientes que están expresadas como fracciones a valor equivalente en números decimales. Observa el siguiente video para comprender el procedimiento de conversión de fracciones a números decimales:

Conversión de fracciones a número decimal (Del minuto 3:36 al 6:39)

3/8 como número decimal.

https://www.youtube.com/watch?v=bKdUhyKLtto

Para conocer el valor equivalente de tres octavos como un número decimal, lo primero que haremos es recordar que toda fracción puede expresarse como el cociente de una división, en este caso del número 3 entre 8. La división puede representarse de la siguiente forma: dado que el número ocho es el divisor y el 3 es el dividendo, por tanto:

Tres octavos es equivalente a trescientos setenta y cinco milésimos. Se escribe un número cero a la izquierda del punto decimal debido a que es un número menor a la unidad o a un entero.

0.375 es equivalente a 3/8.

Observaste que uno de los procedimientos para obtener la expresión equivalente de una fracción en número decimal es dividir el numerador entre el denominador.

Ahora calculemos el primer número decimal de nuestra receta:

División de 1 entre 2.

https://www.youtube.com/watch?v=fj87jlUE4cQ&feature=youtu.be

Por lo tanto, un medio es igual cinco décimos. ½ = 0.5

Vamos a convertir la fracción del siguiente ingrediente a su representación equivalente a número decimal.

División 5 entre 1000

https://www.youtube.com/watch?v=L_B4Q1GFZIc&feature=youtu.be

Para este ejemplo tomaremos la fracción cinco sobre mil y los convertiremos en un número decimal, para eso colocaremos dentro de nuestra galera el numerador que es cinco y fuera de ella mil. El resultado de la fracción cinco sobre mil es cero punto cero, cero cinco, lo cual se lee como cinco milésimos, ese es nuestro resultado.

5/1000 = 0.005

Ahora, por favor determina la representación equivalente en número decimal de los ingredientes restantes.

¿Cómo te fue? Comparemos los resultados.

Realicemos algunas actividades más.

En el primer ejemplo, observaremos que en la aplicación de geometría dinámica tenemos la fracción de 4/5, nuestro numerador es 4 y el denominador es 5, en el gráfico correspondiente observamos que se toman cuatro quintas partes de las que están divididas, por lo tanto, 4 están coloreadas en azul de 5 verdes totales, entonces, hagamos el procedimiento para verificar su equivalencia en número decimal, dividamos el numerador entre el denominador:

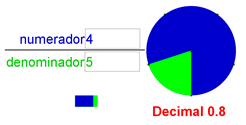
V1 de F a D 4 entre 5
https://www.youtube.com/watch?v=ZVYjm5rm0ls&feature=youtu.be
EJEMPLOS DE CONVERSIÓN DE FRACCIONES A DECIMALES.

Revisemos el procedimiento vamos a dividir cuatro entre cinco.

¿Cuántas veces cabe el cinco en el cuatro?

Cero, vamos a requerir el uso de números decimales, colocamos el punto al lado derecho del dividendo y otro punto en el cociente, por lo tanto, ya podemos agregar tantos ceros decimales como sean necesarios hasta tener un residuo cero o no tener residuo, en este caso, vamos a agregar un cero decimal.

Como ya habíamos dicho el cinco no cabe en el cuatro, pero si cabe en el cuarenta, ¿cuántas veces cabe el cinco en el cuarenta?

¡Muy bien!, ocho, porque ocho por cinco son cuarenta; cuarenta menos cuarenta resulta cero. Como nuestro residuo ya es cero, hemos concluido la división y entonces podemos decir que cuatro quintos es equivalente a cero punto ocho u ocho décimos.

Veamos otro ejemplo como observas tenemos la fracción de un cuarto, nuestro numerador es 1 y el denominador es 4.

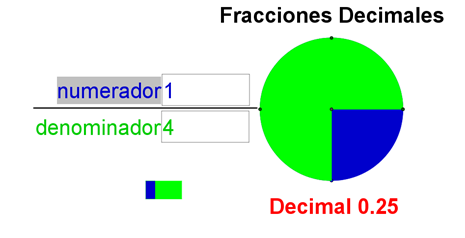
V2 de F a D 1 entre 4

https://www.youtube.com/watch?v=wqe9iN8Vin0&feature=youtu.be

Observamos que solo se va a tomar una cuarta parte en la que está dividida, nota que es la que está coloreada en azul.

Ejemplos de conversión de fracciones a decimales

Hagamos el procedimiento para verificar su valor en número decimal, dividimos el numerador entre el denominador, o sea uno entre cuatro:

¿Cuántas veces cabe el cuatro en el uno?

Cero; vamos a requerir de utilizar números decimales, colocamos un punto a la derecha del divisor y a la derecha del cero del cociente.

Ya podemos agregar un cero decimal, ¿Cuántas veces cabe el cuatro en el diez?

Muy bien, dos, porque cuatro por dos son ocho; diez menos ocho resulta dos.

Debido a que aún tenemos residuo podemos agregar un cero decimal más, agregamos el cero y lo bajamos, ¿Cuántas veces cabe el cuatro en el veinte?

Muy bien, cinco; porque cinco por cuatro es veinte. Veinte menos veinte, resulta cero. Como nuestro residuo ya es cero, hemos concluido con nuestra división y podemos decir que un cuarto es equivalente a cero punto veinticinco o veinticinco centésimos.

En la receta dice que el panqué debe estar en el horno dos cuartos de hora, ¿cuántos minutos debemos esperar para apagar el horno?

Resolvámoslo mediante una aplicación de geometría dinámica.

En esta aplicación se representa un gráfico de un reloj que será nuestra unidad, vemos que está fraccionado en 60 partes iguales que son 60 minutos. Podemos manipular la fracción que representa la hora en el reloj, tanto el numerador como el denominador, ahora se muestran cinco sextos y se lee: “cinco sextos de hora o cinco sextos de 60 minutos”.

Identificamos que se iluminan cinco partes en azul de 6 totales y ya se muestra el resultado que son 50 minutos.

Ahora manipulemos el denominador a diez, y se lee” cinco décimos de hora o cinco décimos de 60 minutos” nota que son 30 minutos, cinco decimos es lo mismo que iluminar en total la mitad del reloj, por lo tanto, es una fracción equivalente a un medio, es decir, cinco décimos es igual a un medio.

Ahora si lo partimos en 4 partes iguales, sería igual a 60 dividido entre 4, por lo tanto, un cuarto es igual a 15 minutos.

Para dos cuartos, entonces, tenemos 30 minutos en total.

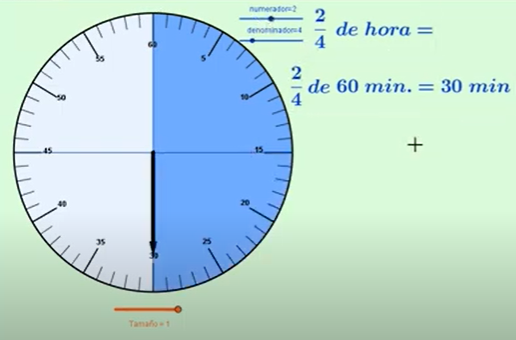
¡El panqué ya está listo!

Observa el siguiente video que te mostrará ejemplos en donde las fracciones tienen diferentes usos, tales como escalas, medidas, proporciones, entre otros.

Otras situaciones que generan fracciones

https://www.youtube.com/watch?v=s8HjqIpjbGM&list=PLR7wXigAnwdbQcsEguX3TRSsjTbvxdyb2&index=6

Resumamos algunos aspectos importantes de esta lección:

Toda fracción puede representar una división de dos números enteros donde se representa una relación entre numerador y el denominador.

La fracción es una parte de un entero donde la representa, siendo “a “y “b” cualquier número natural y “b “diferente de cero (0 ).

En una fracción el numerador puede ser mayor al denominador a > b o viceversa, el denominador podría ser mayor que el numerador b > a.

Un procedimiento para convertir una fracción a número decimal consiste en dividir el numerador entre el denominador esto es a / b y el cociente será el número decimal equivalente a la fracción.

Estos temas los puedes consultar en tu libro de secundaria de Matemáticas de primer grado. Si no lo tienes, puedes acudir a las ligas que se mostrarán abajo o ver de nuevo esta sesión.

¡Buen trabajo!

Gracias por tu esfuerzo.

* Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.

Para saber más:

Lecturas

Vamos de regreso a clases- Cuaderno del estudiante 1° de Secundaria