Capacidad y volumen
Capacidad y volumen
Aprendizaje esperado: calcula el volumen de prismas rectos, cuya base sea un triángulo o un cuadrilátero, desarrollando y aplicando fórmulas.
Énfasis: deducir la fórmula del volumen de prismas rectos para la resolución de problemas.
¿Qué vamos a aprender?
Trabajarás un tema de geometría relacionado con el espacio que ocupa un cuerpo geométrico y con su capacidad, es decir, el volumen. Observarás la equivalencia que existe entre las unidades de capacidad y volumen; por ejemplo, entre el litro y el decímetro cúbico, en diferentes prismas rectos.
¿Qué hacemos?
La natación es un deporte tradicional de los juegos olímpicos, en el que se realizan pruebas de diferentes estilos de nado, seguramente en alguna ocasión, por televisión habrás visto esta competencia y observado el tipo de piscina que se utiliza. Reflexiona sobre las siguientes preguntas: ¿Cuál es la forma que tiene la alberca olímpica?, ¿cuál será el volumen de una piscina en la que se llevan a cabo las competencias de natación?, ¿cuántos litros de agua se necesitarán para llenar una de esas piscinas? Para dar respuesta a las preguntas anteriores, observa la siguiente imagen:

Como puedes ver en la imagen, la piscina tiene 3 carriles, su contorno es de color gris con forma de un rectángulo, y está completamente llena de agua. Se parece a un prisma recto, estos prismas tienen dos bases poligonales congruentes que son paralelas entre sí, además de que tiene una altura o profundidad. Dependiendo de la forma de su base reciben su nombre, por ejemplo, si sus dos bases tienen forma de un triángulo, se llama prisma triangular; si sus dos bases tienen forma de un cuadrado, se llama prisma cuadrangular; si sus dos bases tienen forma de pentágono, se llama prisma pentagonal. Ahora puedes contestar la primer pregunta planteada, ¿cuál es la forma más común que tienen las piscinas? La forma de las piscinas, donde se realizan las competencias de natación, tienen dos bases en forma de rectángulo, de ahí el nombre de prisma rectangular, y tienen cuatro caras laterales, que son paralelogramos.
Para responder la segunda pregunta, debes saber que el volumen es el espacio que ocupa un cuerpo geométrico; y para medirlo, se consideran el largo, el ancho y la altura. En este caso encontrarás el volumen del prisma rectangular. Pero antes debes analizar la siguiente información:
El siguiente cubo fue construido con cubos más pequeños, observa detenidamente, cuenta los cubos pequeños y responde a la pregunta: ¿qué cantidad de cubos hay dentro del cubo más grande?

Puedes calcular el número de cubos sin tener que contarlos, hay que multiplicar el número de cubos pequeños que contiene el cuerpo en el ancho, largo y alto. Es decir, 3 x 3 x 3 = 27 cubos, en total. Ahora, te presentaremos otro cuerpo geométrico formado por cubos. Se trata de un prisma rectangular, ya que su base es un rectángulo:
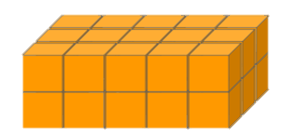
Intenta contar los cubos que conforman al prisma. No olvides que hay algunos cubos que no se logran ver en la imagen debido a que sólo vemos 3 de las 6 caras que conforman al prisma. Recuerda que debes multiplicar el total de cubos que conforman el ancho, largo y alto, lo que nos da como resultado 30 cubos.
Nos movemos en un mundo de tres dimensiones y lo puedes observar al mirar las casas, un carro, un edificio e incluso tu cuerpo; y en muchas ocasiones, el cálculo de este volumen es práctico, pero ¿por qué se comenzó a utilizar la unidad de medida del cubo? Para contestar esta pregunta, observa el siguiente video del minuto: 01:24 al 02:55:
- ¿Por qué el cubo?
https://youtu.be/3f2MHue0I1c
Es interesante saber que la unidad básica del volumen es el metro cúbico. Regresando al ejemplo de la piscina, ¿cuál será la fórmula para calcular el volumen de un prisma rectangular? Para contestar a la pregunta observa el siguiente video del minuto: 03:43 a 05:31: - El volumen de prismas rectangulares
Ahora ya sabes que para calcular el volumen de un prisma recto debes utilizar la siguiente fórmula:

Volumen = Área de la base por altura.
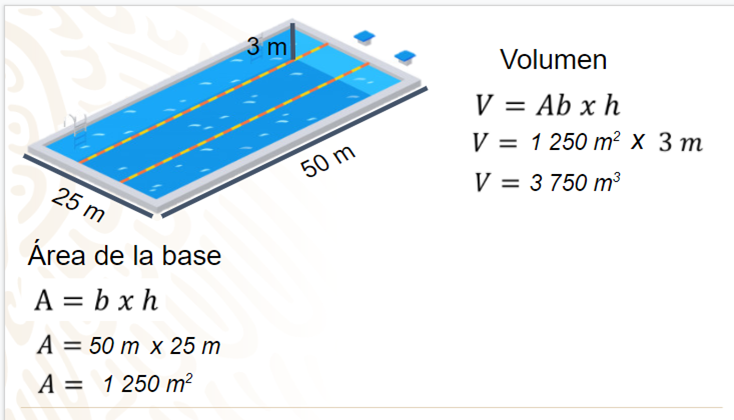
Con esta información podrás calcular el volumen de la piscina. Te sugerimos repliques en tu cuaderno, o en hojas reutilizables, el esquema de la piscina.

Como puedes ver en la imagen, las medidas que tiene la piscina son: 3 metros de profundidad, 50 metros de largo y 25 metros de ancho, como lo recomienda la Federación Internacional de Natación (FINA) para competencias. Primero obtén el área de la base, es decir encuentra el área del rectángulo y posteriormente encuentra el volumen, multiplicando el área de la base por la altura de la piscina.
Queda una pregunta por responder: ¿cuántos litros de agua se necesitarán para llenar la piscina? Antes de darle respuesta a esta pregunta, revisa la relación que tiene la capacidad con respecto al volumen. Estos términos se encuentran estrechamente relacionados ya que la capacidad es el espacio vacío que tiene un objeto para contener a otra u otras cosas dentro de éste, a diferencia del volumen, que es el espacio que ocupa un cuerpo, es por ello que entre ambos conceptos existe una relación de equivalencia; que está basada entre el litro, que es una unidad de capacidad y el decímetro cúbico que es una unidad de volumen. Realiza el siguiente experimento:
- Construye un recipiente en forma de cubo que mida exactamente 10 cm de lado. Recuerda que en un cubo todas sus caras son cuadradas; además en este caso, su medida deberá ser de 10 cm por lado, que es igual a 1 decímetro, por lo que su volumen es de un decímetro cúbico.
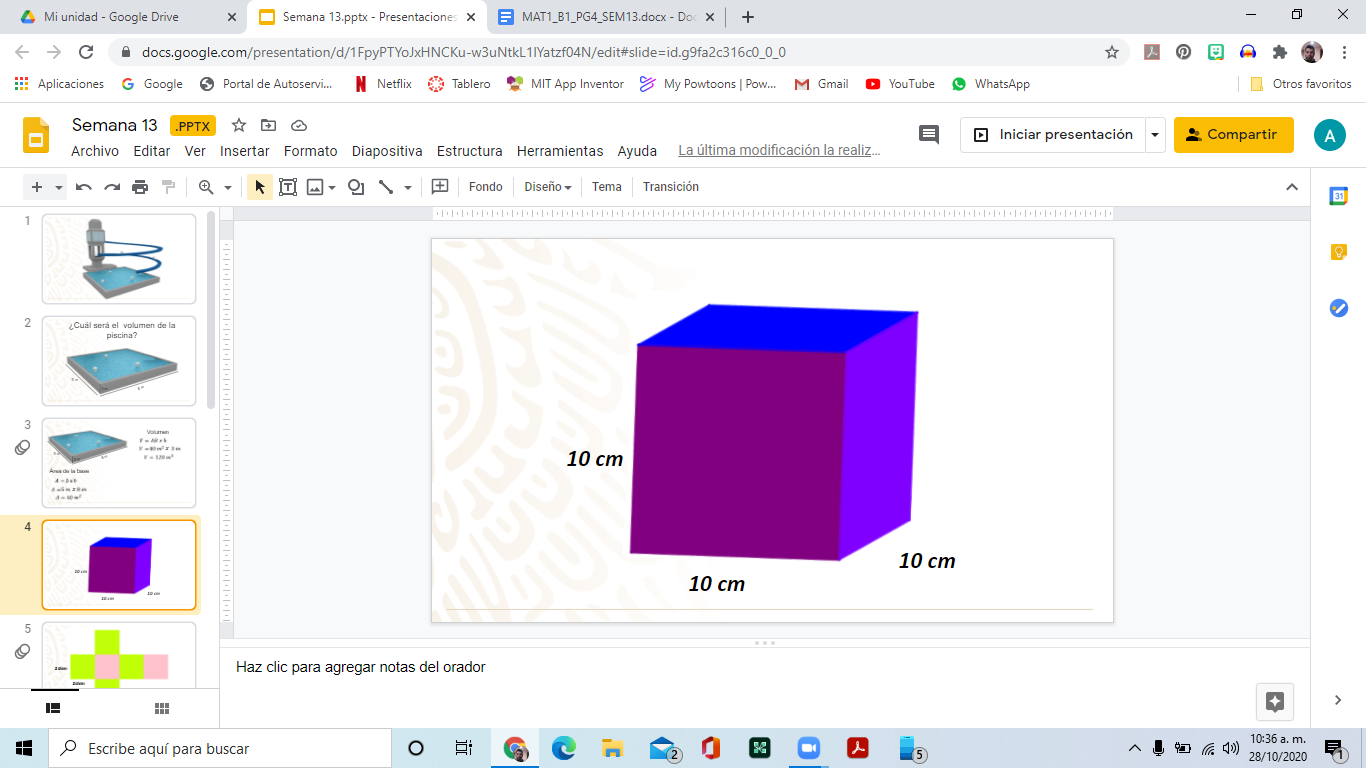
Para hacerlo, observa el desarrollo plano que se muestra a continuación:
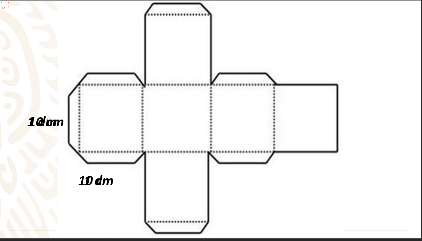
Observa que está formado por una fila de 4 cuadrados cada uno de 10 centímetros por lado, o lo que es igual 1 decímetro por lado y en la parte superior un cuadrado, que será la tapa del cubo así como en la parte inferior otro cuadrado que actuará como el fondo o la base. Con este molde podrás hacer un cubo, solamente tendrás que trazar, doblar y pegar el desarrollo plano en algún material que sea de fácil manejo, pero resistente a doblarse con el peso del agua. Además, tendrás que prever, cómo pegarás cada una de las caras, en el caso de que lo hagas con cartón o cartulina, hay que añadir el espacio en el que colocarás las “pestañas”, es decir, las extensiones en algunos de los lados que te permitirán unir todas las caras.
Una vez que lo hayas realizado, vierte agua en el cubo, y podrás observar a este recipiente le cabe, exactamente, un litro de agua.
Sabemos que este recipiente mide 1 dm cúbico, pero que esta misma medida se puede expresar en centímetros, ¿cuántos centímetros cúbicos podrían caber en el cubo de 1 decímetro cúbico?
10 de largo x 10 de ancho y 10 de alto, un total de: 1000 centímetros cúbicos. Eso quiere decir, que un recipiente de 1000 centímetros cúbicos tiene una capacidad de un litro de agua. Es exactamente la misma cantidad de mililitros que se necesitan para formar un litro, es decir, un mililitro es equivalente a un centímetro cúbico. Esto quiere decir que tenemos otra equivalencia.
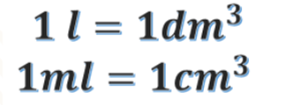
Ahora ya sabes que 1 litro es igual a 1 decímetro cúbico, y que 1 mililitro es igual a 1 centímetro cúbico.
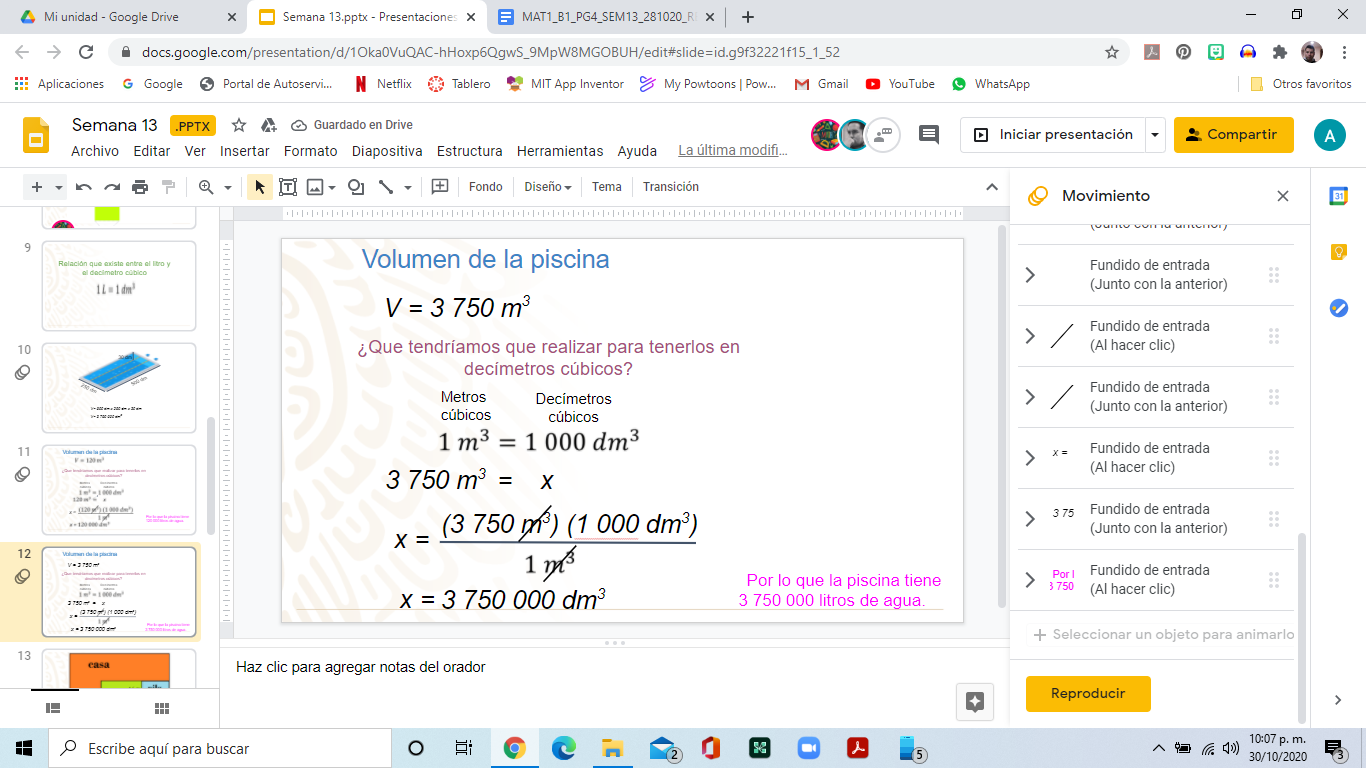
Retomando el problema principal, para encontrar los litros de agua que tiene la piscina utilizarás la relación que se acaba de demostrar entre el litro y el decímetro cúbico, ten muy presente que la equivalencia es: 1 litro igual a 1 decímetro cúbico. Pero el volumen que calculaste de la piscina está en metros cúbicos, tienes que realizar la conversión a decímetros cúbicos. El procedimiento es el mismo, debes multiplicar las 3 dimensiones.
Un metro equivale a 10 decímetros, así que las dimensiones de la piscina en decímetros son: ancho mide 250 decímetros, de largo 500 decímetros y de altura 30 decímetros. Multiplica las 3 medidas y obtendrás como resultado 3,750,000 decímetros cúbicos. Y como un litro es igual que un decímetro cúbico, entonces la alberca tiene capacidad de 3,750,000 litros.
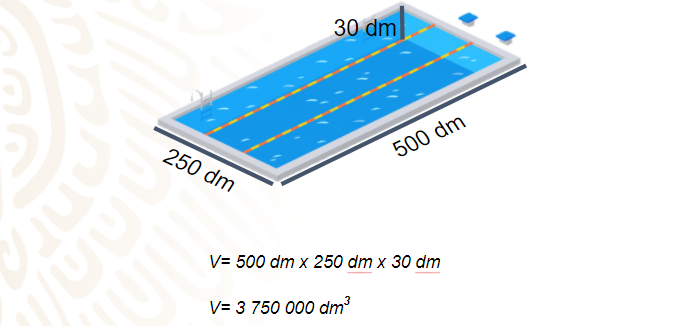
Puedes obtener este resultado de otro modo: un metro cúbico es igual a mil decímetros cúbicos; ya que, haciendo la conversión a decímetros, tendrías que multiplicar las tres dimensiones del cuerpo geométrico; 10 decímetros representan 1 metro por lo que 10 dm x 10 dm x 10 dm es igual a 1000 decímetros cúbicos o 1 metro cúbico es igual a 1000 litros. Realiza una regla de tres, debes multiplicar 3 750 metros cúbicos por 1000 decímetros cúbicos y dividir entre 1 metro cúbico, cuando tienes la misma unidad de medida en el numerador y en el denominador, puedes simplificarlas, ya que en el numerador están multiplicando y en el denominador dividiendo, siendo estas operaciones inversas, quedando solamente decímetros cúbicos. Ahora efectúa el producto 3,750 x 1,000 = 3,750,000 entre uno, lo que da como resultado 3,750,000 decímetros cúbicos; por lo tanto, si ya sabes que un decímetro cúbico tiene una capacidad de un litro. La piscina se llena con aproximadamente 3,750,000 litros de agua.
En algún momento puedes utilizar este conocimiento para poder planear, construir y sacar provecho de situaciones problemáticas; como la siguiente:
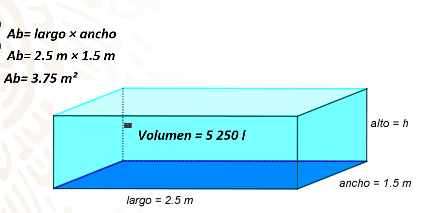
Mariana, quiere construir una pileta y dispone de un espacio en su patio con las siguientes medidas:

En la imagen puedes observar el espacio que ocupa la construcción de la casa de Mariana, el patio y el espacio para la pila de agua, será de 2.5 metros de largo por 1.5 metros de ancho. Ahora, ya que Mariana quiere que esa pila tenga una capacidad de por lo menos 5,250 litros de agua. ¿Cuál será la altura mínima que debe tener la pila para que pueda contener esa cantidad de agua?
Analiza los datos para poder resolver el problema y conocer la altura mínima que se necesita:
El largo es igual a 2.5 metros, el ancho es igual a 1.5 metros, se desconoce la altura y la representaremos con una h, recuerda que se cuenta con la referencia de Mariana, que indica que requiere una cantidad mínima de 5,250 litros en la pila.
En este caso, al ser una base rectangular, vas a obtener el área de la base con la fórmula que consiste en multiplicar el largo por el ancho. Por lo tanto, 2.5 x 1.5, obteniendo así el producto 3.75 m2.
Para continuar vas a convertir los litros en metros cúbicos. Sabes que un metro cúbico es igual a 1,000 litros y se desconoce el volumen necesario para contener un total de 5,250 litros; multiplica 5,250 x 1 y divídelo entre mil, así obtienes que es igual a 5,250m³, ése es el volumen que necesario.

Con estos datos puedes, sustituir en la fórmula de volumen y encontrar el valor de la altura. En volumen anota 5,250 metros cúbicos, eso se obtiene de multiplicar el área de la base que es 3.75 por la altura que está representada por la letra “h”. Recurre a las propiedades de la igualdad para despejar a la literal y tienes que 5,250 entre 3.75 es igual a la altura, y después de obtener el resultado observa que la altura de la pila deberá ser de un mínimo de 1.4 metros.

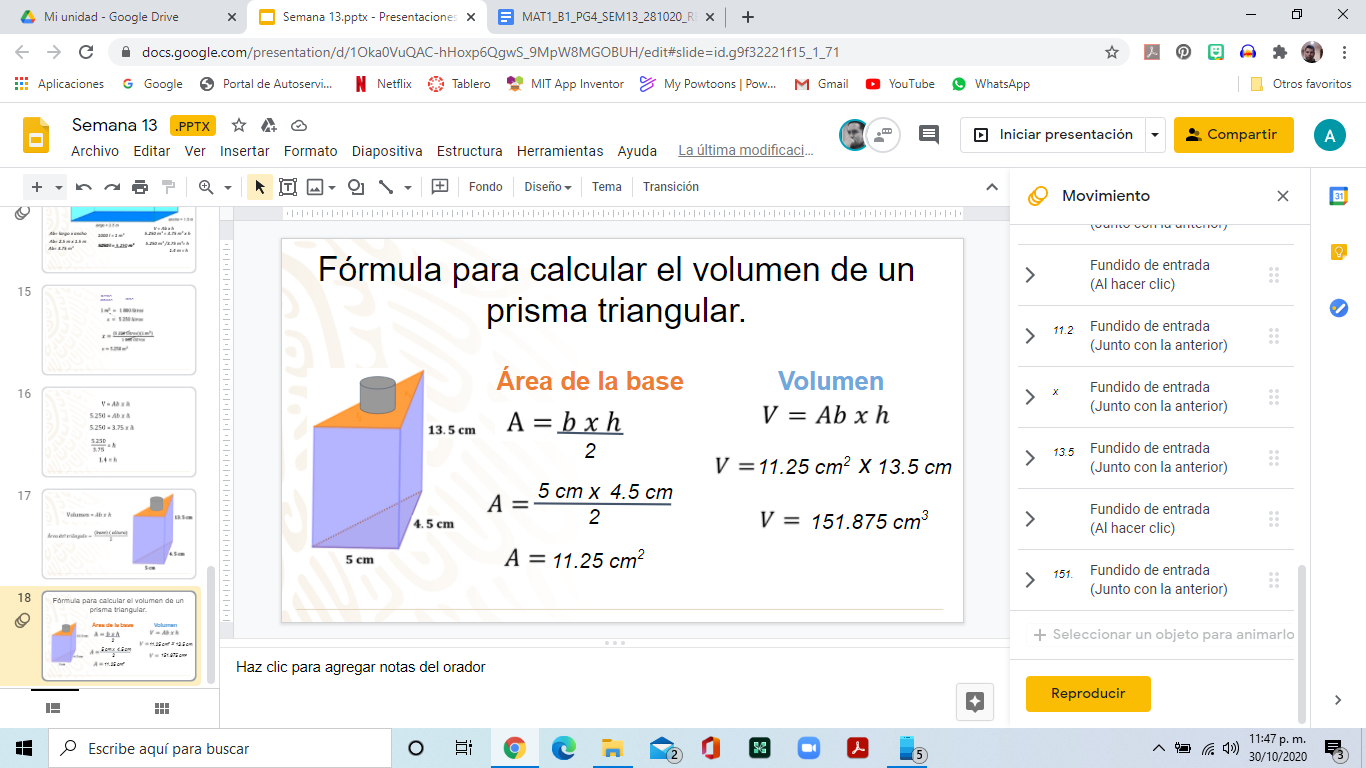
Ya revisaste con algunos prismas rectangulares, que también son conocidos como paralelepípedos. Ahora analiza un prisma triangular, usando de ejemplo un envase de perfume con esa forma. Te has preguntado ¿Cómo puedes calcular cuántos mililitros contiene?
Para obtener los mililitros hay que encontrar el volumen, y ocuparás la misma fórmula que has usado con anterioridad, área de la base por altura. La diferencia es que la base es un triángulo y para obtener su área multiplica la base del triángulo por altura entre dos.

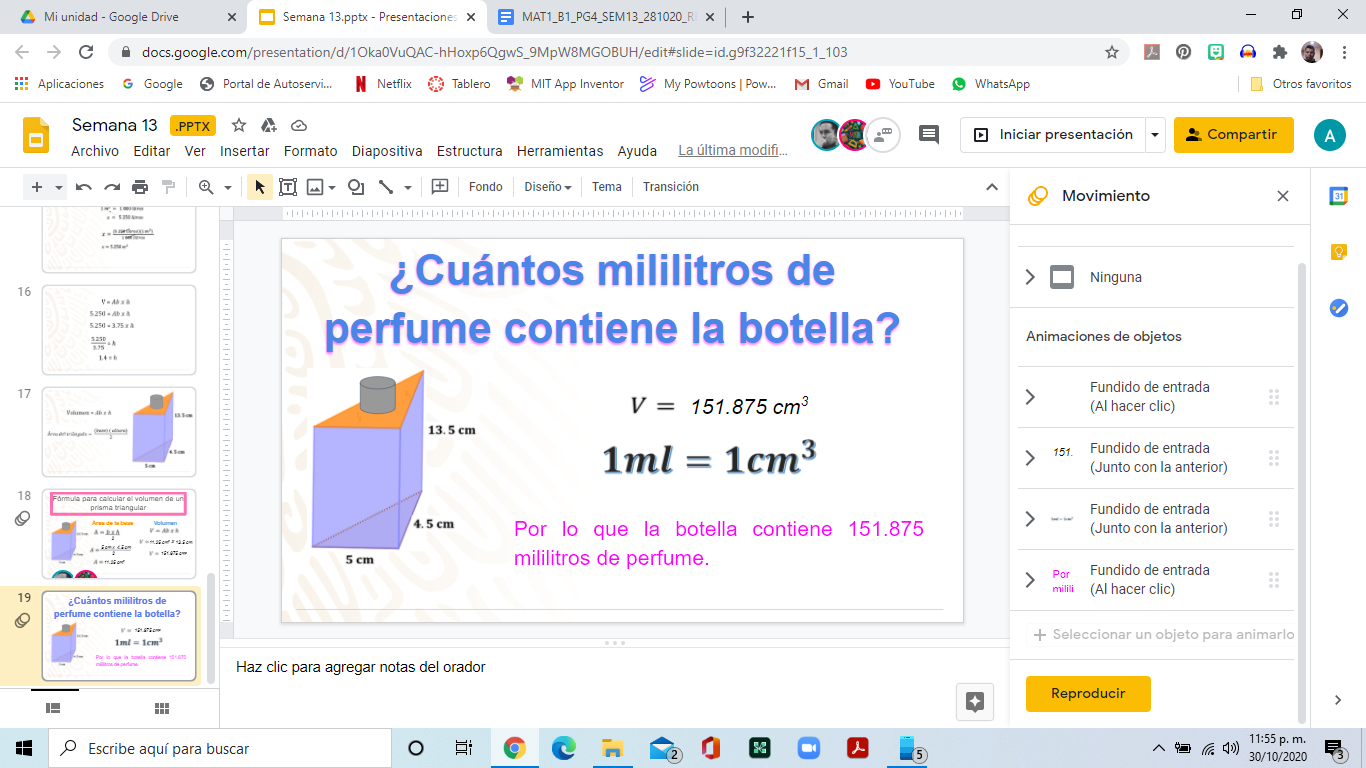
La base del triángulo mide 5 cm y su altura es de 4.5 cm. Multiplica 5 cm por 4.5 cm que es igual a 22.5 cm2, lo divides entre dos, y el obtienes 11.25 cm2. Ahora lo multiplicas por la altura del prisma que es 13.5 cm, dando como resultado 151.875 cm cúbicos.
¿Cuántos mililitros de perfume tiene la botella? Como lo viste anteriormente 1 centímetro cúbico equivale a 1 mililitro por lo que la botella contiene 151.875 mililitros de perfume.
Se realiza lo mismo en cada prisma del que quieras calcular su volumen, así puedes determinar que, en todos los prismas, multiplicarás el área de la base por la altura, para obtener su volumen. Siempre ten presente que los prismas son aquellos cuerpos cuyas caras laterales son rectángulos, y dependiendo de sus bases su nombre cambia, podrás tener prisma triangular con base de triángulo, prisma hexagonal con la base en forma de hexágono, prismas octogonales; entre muchos otros.
El reto de hoy.
Te invitamos a que tomes tu libro de matemáticas y consultes las actividades que ahí se proponen, seguramente observarás situaciones muy interesantes sobre este tema.
¡Buen trabajo!
Gracias por tu esfuerzo.