Cálculo de valores faltantes
Cálculo de valores faltantes
Aprendizaje esperado: calcula el volumen de prismas rectos cuya base sea un triángulo o un cuadrilátero, desarrollando y aplicando fórmulas.
Énfasis: calcular valores faltantes al aplicar la fórmula del volumen de prismas rectos.
¿Qué vamos a aprender?
En esta sesión, el aprendizaje esperado es “Calcula el volumen de prismas rectos cuya base sea un triángulo o un cuadrilátero, desarrollando y aplicando fórmulas”.
Retomarás algunos conocimientos sobre el tema de “Cálculo de valores faltantes”. Para lograrlo, realizarás diversas actividades con la finalidad de precisar algunas particularidades sobre este interesante tema.
En esta sesión, expondrás algunas situaciones de la vida cotidiana, en las podrías enfrentarte a la necesidad de calcular un dato faltante, conociendo el volumen de un cuerpo geométrico.
Para lograr un mejor desempeño en las actividades, te recomiendo tener a tu disposición:
●Cuaderno, o bien, hojas reutilizables
●Lápiz
●Goma
●Y tú libro de texto de la asignatura de Matemáticas de primer grado.
¿Qué hacemos?
Realiza una pequeña semblanza del matemático Arquímedes de Siracusa, Entre sus anécdotas más famosas se encuentra la famosa frase “Eureka”. Cuenta el arquitecto e ingeniero romano Vitruvio, que en cierta ocasión el rey Herón II de Siracusa ofreció una gran cantidad de oro a un orfebre, para que le hiciera una corona de oro puro. Cuando la corona estuvo terminada el rey comenzó a sospechar que el orfebre no había empleado todo el oro en la corona, y por tanto había sisado, es decir cortado parte de él.
Herón II le planteó el problema a Arquímedes y éste se puso manos a la obra. Al no poder fundir la corona para calcular su masa y volumen, el problema se antojaba complicado. Sin embargo, mientras tomaba un baño, notó que el agua de la bañera se desplazaba cuando él se introducía en ella. De esta forma comprendió que, si introducía un volumen dentro del agua y medía la altura que alcanzaba ésta, podría determinar el volumen de la corona y por tanto su densidad.
Cuenta la historia que Arquímedes se puso tan contento al descubrir esto, que salió de la tina donde se estaba bañando y desnudo fue corriendo por las calles de la ciudad gritando: ¡Eureka! ¡Eureka! (en griego, “lo conseguí”).
Cuando llegó al palacio, sumergió la misma cantidad de oro puro que el rey había entregado al orfebre y midió la altura del agua. Al introducir la corona notó como la altura era menor. De esta forma, al ser el volumen igual, la única explicación era que las densidades eran diferentes. Finalmente, el orfebre confesó que había quitado oro y agregado plata en la fabricación de la corona.
Arquímedes es conocido como una de las figuras más ilustres en ciencias y matemáticas de la antigüedad.
Si deseas saber más de Arquímedes de Siracusa no dudes en investigar todas sus aportaciones que hasta la fecha son utilizadas como el volumen, que es el tema a tratar en esta sesión.
Como puedes ver el cálculo del volumen data de muchos siglos atrás.
Este contenido ya lo has trabajado antes, ahora es momento de retomarlo conociendo las fórmulas y las utilizarán para calcular valores faltantes.
Recuerda que las fórmulas para calcular perímetro, área y volumen, son expresiones algebraicas que permiten generalizar sobre los procedimientos para realizar dichos cálculos.
Inicia recordando las fórmulas que se utilizan para calcular el volumen de prismas rectos, a partir de los cuales encontrarás alguna de las dimensiones del prisma, conociendo otras y su volumen.
La imagen muestra a un prisma rectangular, como sabes, la fórmula para calcular su volumen es V = área de la base por altura, en este caso se concoe la información necesaria para calcular el área de la base pues al multiplicar 4.5 centímetros por 7 centímetros da como resultado 31.5 centímetros cuadrados y se sabe que el volumen del prisma rectangular es 283.50 centímetros cúbicos.
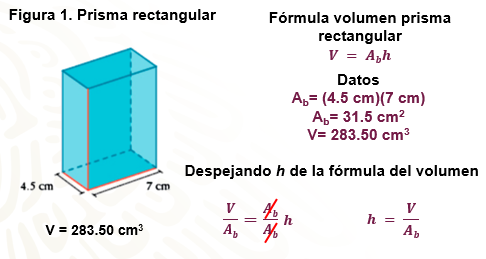
En este caso, se desconoce la medida de la altura. ¿Qué puedes hacer para obtener esa medida?
Tienes que despejar a la altura (h) en la fórmula. Como el área de la base está multiplicado por h, para despejarla, se dividen ambos lados de la igualdad entre Ab, quedando volumen entre área de la base igual a área de la base entre área de la base por altura, por lo tanto, la altura es igual a volumen entre área de la base.

Ahora, sustituyes los valores que se tienen en la expresión obtenida y resuelves la operación, h es igual a 283.50 entre 31.50 igual a 9. Por lo tanto, la altura del prisma rectangular es igual a 9 cm.
Ahora analiza el siguiente caso, para que reflexiones al respecto.
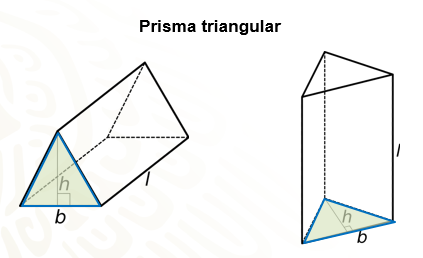
Observa la imagen que muestra al mismo prisma en diferentes posiciones. Podría pensarse que en el primer caso la base es un rectángulo porque en ella está apoyado el prisma, cosa que es falsa, por ello, es importante que tengas claro que un prisma recto tiene dos bases o caras que son paralelas y tantas caras laterales como lados tienen sus bases, sin importar la posición en la que se encuentre, así que tienes que ser cuidadoso al considerar las dimensiones correctas para calcular el volumen.
Ahora, calcula su altura
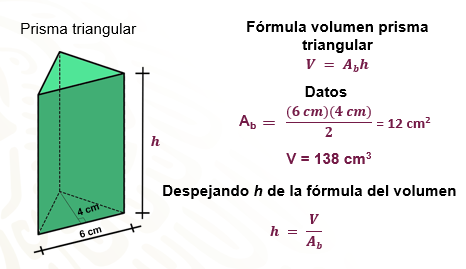
Observa si se cuenta con los datos necesarios para calcular el área de su base:
Base del triángulo 6 centímetros
Altura del triángulo 4 centímetros
Entonces, multiplicas 6 cm por 4 cm y divide entre dos que da como resultado 12 cm2.
Ya tienes que la medida del área de la base y sabes que el volumen del prisma es de 138 cm3.
Y al despejar la altura, se tiene que h = volumen entre área de la base.
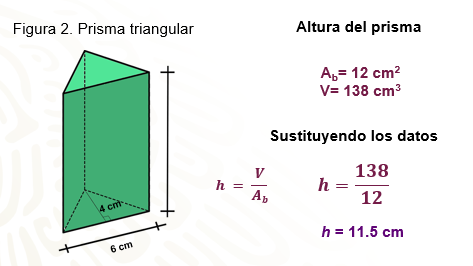
Muy bien ahora que ya tienes despejada la altura en la fórmula, sustituyes los datos conocidos para efectuar las operaciones, en este caso “h” es igual 138 cm3 entre 12 cm2 que es igual a 11.5 cm, que representa la altura del prisma.
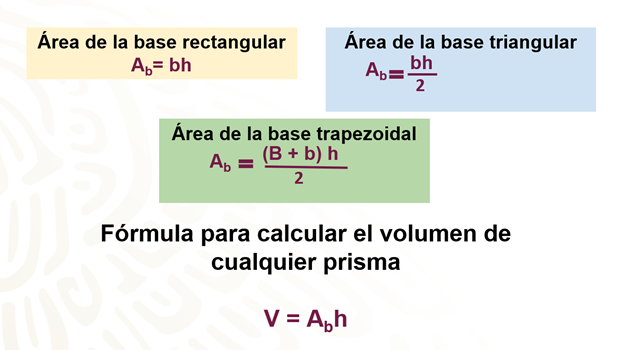
Como has visto hasta ahora, la fórmula para calcular el volumen es la misma para todos los prismas rectos, lo único que cambia es la fórmula que utilizamos para calcular el área de la base. Con esta información, observa la siguiente situación.
¿Sabías que el sector minero-metalúrgico en México en 2018 contribuyó con el 2.4 por ciento del Producto Interno Bruto Nacional?
México ocupa el primer lugar en la producción de plata a nivel mundial.
Se ubica entre los 10 principales productores de 16 diferentes minerales: plata, bismuto, fluorita, celestita, cadmio, molibdeno, plomo, zinc, diatomita, sal, barita, grafito, yeso, oro y cobre. Si quieren conocer más información al respecto los invito a consultar su libro de geografía o comentar con su maestra o maestro a distancia sobre este importante tema.
Y para continuar con el tema analiza la siguiente situación.

Un lingote es una barra de metal principalmente de hierro, plata, oro o platino En la imagen vemos un lingote de oro que tiene forma de prisma recto, cuya base es un trapecio.
Si el volumen del lingote es de 1 350 cm3, ¿Cuánto mide el área de la base del lingote, que corresponde a la base del prisma trapezoidal?
Recuerda que el volumen del lingote es de 1 350 cm3 y la altura es de 30 cm por lo que en la fórmula del volumen de un prisma, debes despejar el Ab quedando al expresión:
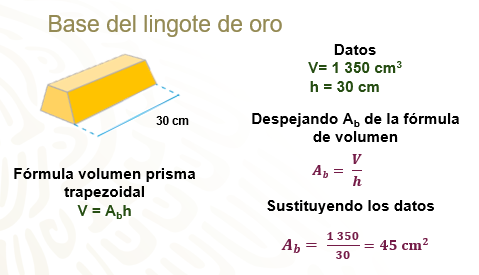
Área de la base igual a volumen entre altura. Ahora sustituye los valores que se conocen en este caso el volumen de 1 350 cm3 y altura que es igual a 30 cm al realizar la división de 1 350 entre 30, se encuentra que el área de la base del prisma es igual a 45 cm2.
A partir de la información que se tiene, te pregunto: si sabes que las bases del trapecio miden 8 cm y 10 cm, ¿cuánto mide la altura de la base del prisma?
¿Cómo la obtienes?

Recuerda que la fórmula para calcular el área de un trapecio es igual a la suma de la mayor más base menor por altura entre dos. Y se sabe que la base mayor mide 10 cm y la base menor, 8 cm y que el área de la base del prisma es igual a 45 cm cuadrados. Por lo que se está listo para sustituir estos valores y realizar los pasos necesarios para despejar a h.
Escribe, 45 es igual a 10 más 8 por h entre dos, para despejar a h, primero multiplicas por 2 a ambos miembros de la igualdad quedando 45 por dos iguales a (18) h entre dos por dos.
A continuación, realiza las operaciones indicadas y obtienes 18h entre 18 igual a 90 entre 18, con lo que se llega al resultado, la altura de la base del prisma trapezoidal es de 5 cm.
Por último, las siguientes preguntas al respecto de este problema.
Si cada centímetro cúbico de oro pesa 19.32 gramos, ¿cuál es la masa del lingote de oro?
Si 100 gramos de oro se venden en 79 675 pesos, ¿cuál es el precio del lingote de oro?
Más adelante podrán verificar sus respuestas.
Continúa explorando sobre lo que produce México, pero ahora lo dirigirás hacia la forma en la que es transportada la mercancía.
En el contexto del transporte de mercancías vía marítima se utilizan buques graneleros que son los más apropiados para transportar cargas sólidas a granel, es decir, a gran escala, recuerda que se habla sobre los minerales que se producen. Estos buques utilizan contenedores, como los que se muestran en la imagen, con forma de prisma rectangular para transportar las mercancías.
Existen contenedores de diferentes medidas. Por ejemplo, algunos tienen un volumen es de 69 m3 y su largo es de 12 m.
¿Cuánto mide el área de la base? ¿Qué tienes que hacer para calcularla?
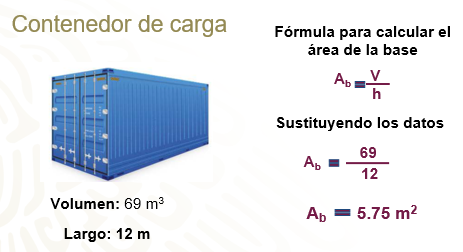
El prisma del que estamos hablando es rectangular, como se vio antes, despeja el área de la base en la fórmula y tienes que es igual a volumen entre “h”, sustituyes los datos que se tiene en este caso volumen es igual a 69 entre 12 m que es igual a 5.75 m2, se puede dar respuesta a la pregunta inicial ¿Cuánto mide el área de la base?
Como observaste en el desarrollo de la situación problema la respuesta es 5.75 m2
Ahora observa, si un productor requiere transportar 50 de estos contenedores, ¿qué volumen del buque ocupará su carga? ¿Cómo puedes averiguarlo?
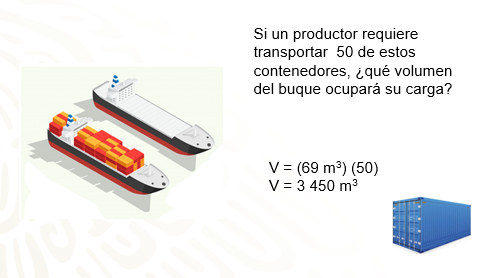
Todo lo que debes hacer es multiplicar el volumen de un contenedor por 50 y entonces realizas la siguiente operación (50) (5.75) es igual a 3 450, ahora ya sabes que el volumen que ocupan 50 contenedores es igual a 3 450 m cúbicos.
Pues llegó el momento de verificar sus resultados respecto a los lingotes de oro.

Para la primera pregunta: ¿Cuál es la masa del lingote de oro?
Se sabe que cada centímetro cúbico de oro pesa 19.32 gramos, para poder obtener su masa se debe realizar una multiplicación, el volumen del lingote por la masa de cada centímetro cúbico, obteniendo 1 350 por (19.32) = 26 082, ahora ya conoces que la masa del lingote es de 26 082 gramos, que es igual a 26.082 kilogramos.
Observa con la siguiente pregunta: ¿Cuál es el precio del lingote de oro?
Se sabe que 100 gramos de oro se venden en 79 675 pesos, por lo tanto, 1 kg se vende en 796 750 pesos y como su masa es de 26.082 kilogramos, su costo es de 796 759 por 26.082 igual a 20 780 833.50 pesos.
Ahora, es momento de hablar sobre momentos de descanso y recreación, observa la siguiente situación:
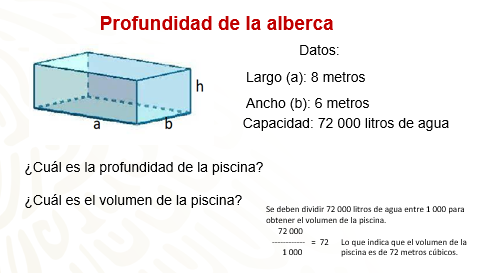
En una piscina con forma rectangular mide 8 metros de largo y 6 metros de ancho y se sabe que para llenar la piscina se necesitan 72 000 litros de agua.
¿Cuál es el volumen de la piscina?
¿Cuál es la profundidad de la piscina?
Para iniciar con el planteamiento del problema, observa cuales son los datos con los que se cuenta:
Litros de agua en la piscina 72 000
Largo de la piscina 8 metros
Ancho de la piscina 6 metros.
Aunque no son lo mismo, el volumen y capacidad tienen una estrecha relación.
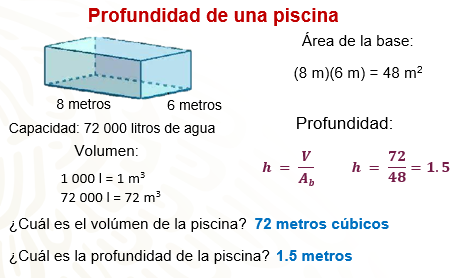
Se sabe que 1 000 litros ocupan un volumen de un metro cúbico, por lo tanto 72 000 litros tienen un volumen de 72 metros cúbicos.
Como esto ya se respondió la primera pregunta.
Bien ahora ya se cuenta con un dato más, que es el volumen de la alberca, lo que te permite sustituir obtener la profundidad de la alberca, que representa a la atura del prisma.
Calcula el área de la base que es igual a 8 por 6 igual a 48 metros cuadrados. Posteriormente sustituimos los valores que tenemos para calcular la altura (h), que es h = volumen entre área de la base, obteniendo la operación 72 entre 48 que es igual a 1.5.
1.5 = h
Ahora sí, da respuesta a la segunda pregunta del problema.
¿Cuál es la profundidad de la piscina?
La profundidad es de 1.5 metros
Si el dato faltante este problema fuera otro, ¿el procedimiento correspondiente sería el mismo de los que ya se conoce?
Si se conocen tres datos del mismo prisma, siempre es posible obtener el cuarto valor.
Para que quede más claro observa nuevamente el prisma rectangular que representa a la alberca.
Ahora, se sabe que el largo mide 8 metros, que tiene 1.5 metros de profundidad y que su volumen es de 72 metros cúbicos.
¿Cómo se puede obtener la medida del ancho de la base?

Para calcular dicha medida se realiza lo siguiente.
De acuerdo con las literales que muestra la imagen, el volumen del prisma es V = (a) por (b) por (h)
Si sustituyes las literales por los valores que tienes, resulta que: 72 = (b) por (8) por (1.5)
Se realiza la operación del lado derecho, obteniendo: 72 = 12b.
Es momento de despejar a la incógnita “b”, en este caso se dividen ambos miembros entre 12, lo que permitirá conocer el ancho de la alberca: 72 entre 12 es igual a 12a entre 12. Se realizan las operaciones y el resultado es 6 = b.
El valor del lado “b” es igual 6, es decir, el ancho de la alberca mide 6 metros.
Ya observaste que obtienes el mismo valor del primer ejercicio relacionado con la piscina.
Observa otra situación problema.
El Departamento de mercadotecnia de una fábrica de cajas detectó que varios clientes pedían cajas que tuvieran dos veces, tres veces o cuatro veces más volumen que la caja estándar que se muestra en la imagen a continuación:
¿Cuál es el volumen de la casa estándar?
Bien observas primero cuales son las dimensiones de la caja, llama “a” y “b” a los lados de la base y “h” a la altura, entonces se tiene que:
a = 20 centímetros
b = 30 centímetros
h = 25 centímetros
Por lo que se sustituye la fórmula
V = (a) (b) (h)
Obteniendo
V = (20) (30) (25)
Se realiza la multiplicación dando como resultado que el V = 15 000 centímetros cúbicos.
Ahora bien, para saber cuáles son las dimensiones que se requieren para fabricar las cajas con las medidas solicitadas por los clientes, observa lo siguiente:
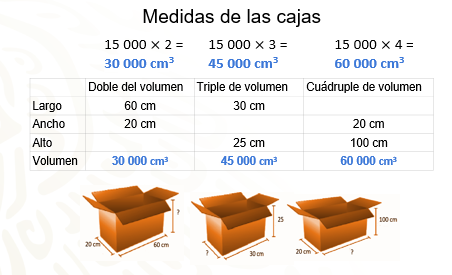
Para obtener el volumen de cada caja a fabricar, primero se debe saber cual le corresponde a cada una, tomando en cuenta que la caja estándar que ya fabrican tiene un volumen de 15 000 centímetros cúbicos, por lo que se realiza una multiplicación de la siguiente manera. Para la caja con doble volumen, se multiplica: 15 000 por (2) = 30 000 centímetros cúbicos.
La siguiente: 15 000 (3) = 45 000 centímetros cúbicos, en este caso se multiplica por tres porque el cliente solicita que tenga el triple de volumen.
Por último:
15 000 por 4 = 60 000, se multiplica por 4 ya que el cliente solicita que la caja tenga el cuádruple de volumen que la caja estándar.
Para cada caja, ya se establecieron dos medidas, toma nota de la información calcula los valores faltantes aplicando los procedimientos vistos.
Ahora conociendo los volúmenes de cada caja y con las medidas que ya se dieron a conocer en la tabla podrás obtener el dato faltante de cada caso,
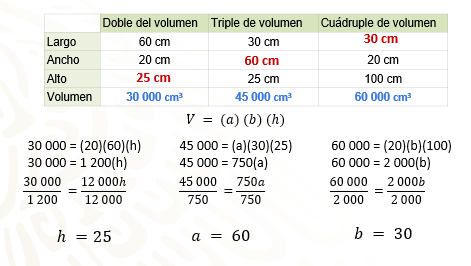
Inicia con la caja que tiene un volumen de 30 000 cm cúbicos y nos falta calcular la altura.
Sustituye la fórmula de volumen que como ya has visto: V = ancho (a) por largo (b) por altura (h)
Sustituye los valores conocidos:
30 000 = (20) (60) (h), realizas la multiplicación de los lados de la caja obteniendo 30 000 = 1200 (h)
Se despeja la fórmula para encontrar el valor de la altura, en este caso se divide entre 1200 ambos miembros, 30 000 entre 1 200 igual a 1 200 “h” entre 1 200; se realizan las operaciones obteniendo
h = 25. La altura de esta caja debe medir 25 cm
Ahora el valor faltante es el ancho (a), entonces se tiene que: 45 000 = (a) (30) (25)
Se realiza la multiplicación obteniendo que 45 000 = (a) (750) se despeja la literal que en este caso es el ancho de la caja, dividiendo entre 750 ambos miembros, se realizan las operaciones obteniendo a = 60, que representa el ancho de la caja en centímetros.
El reto de hoy:
Realiza el cálculo de la última caja cuyo volumen es igual a 60 000.
No olvides que se debe iniciar sustituyendo los valores conocidos en la fórmula de volumen
60 000 = (20) (b) (100)
Se realiza la multiplicación
60 000 = 2 000 (b)
Se despeja b que en este caso es el lado más largo de la caja, por lo que se dividen ambos miembros entre 2 000, se realizan las operaciones obteniendo el valor del lado más largo de la caja, que en este caso es b = 30 centímetros.
Ahora el departamento de mercadotecnia sabe cuáles son las medidas que requiere para cada caja respetando el volumen que ha sido solicitado por cada uno de los clientes.
Recuerda que si tienes alguna duda sobre el tema deben acercarse a tu maestro o maestra a fin de que les apoye o bien consultar tu libro de texto.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas