Cálculo de porcentajes II
Cálculo de porcentajes II
Aprendizaje esperado: resuelve problemas de cálculo de porcentajes, de tanto por ciento y de la cantidad base.
Énfasis: obtener el porcentaje que representa una cantidad de otra. Calcular porcentajes mayores que 100%.
¿Qué vamos a aprender?
En esta sesión descubrirás cómo las artesanías de una región purépecha se relacionan con el objetivo matemático de la sesión relacionada con el cálculo de porcentajes, para cumplir con el aprendizaje esperado “Resuelve problemas de cálculo de porcentajes, de tanto por ciento y de la cantidad base”.
¿Qué hacemos?
Como sabes, México es un país rico en biodiversidad y cultura, la rica gastronomía mexicana es reconocida a nivel mundial como patrimonio inmaterial de la humanidad. De igual manera, se tienen múltiples oficios reconocidos a nivel mundial, entre ellos la artesanía de cobre martillado que caracteriza al pueblo de Santa Clara del Cobre, en el estado de Michoacán.

En esta sesión a descubrirás cómo está artesanía de una región purépecha se relaciona con el objetivo matemático de la sesión el cual es: “Obtener el porcentaje que representa una cantidad de otra y calcular porcentajes mayores que 100%”.
Los porcentajes han formado parte de la vida cotidiana. Quizás no lo percibas directamente, pero en cada producto o servicio que consumes lleva implícito algún tipo de impuesto que se maneja en un porcentaje dependiendo del costo del producto o servicio.
Para lograr el aprendizaje de esta sesión se comenzará con la resolución de ejercicios y problemas para adquirir las herramientas que necesitas.
Retomando las artesanías de cobre martillado del pueblo de Santa Clara del Cobre, se estimarán algunos porcentajes de la materia prima de esta artesanía.
El precio promedio del cobre puro o de primera, estimado por el Sistema Integral sobre Economía Minera es de 160 pesos el kilogramo, pero las artesanías que se fabrican en Santa Clara del Cobre utilizan en su mayoría cobre reciclado o de segunda de algunas otras piezas ya fabricadas previamente, que se compran en distintos precios, dependiendo de su procedencia. El promedio de esta materia prima se estima en 97 pesos el kilogramo.

Se utilizarán estos datos para comparar el ahorro que tienen los artesanos al utilizar un material reciclado. ¿Qué porcentaje del precio del cobre reciclado representa el precio del cobre puro?
Sabes que el precio del cobre puro oscila entre 160 pesos por kilogramo y que el cobre reciclado está aproximadamente en 97 pesos. Como el punto de comparación se realiza a partir del cobre reciclado, se le asignarán a 97 pesos el 100%.
Primero se organizará esta información en una tabla para establecer una relación entre el precio y porcentaje.
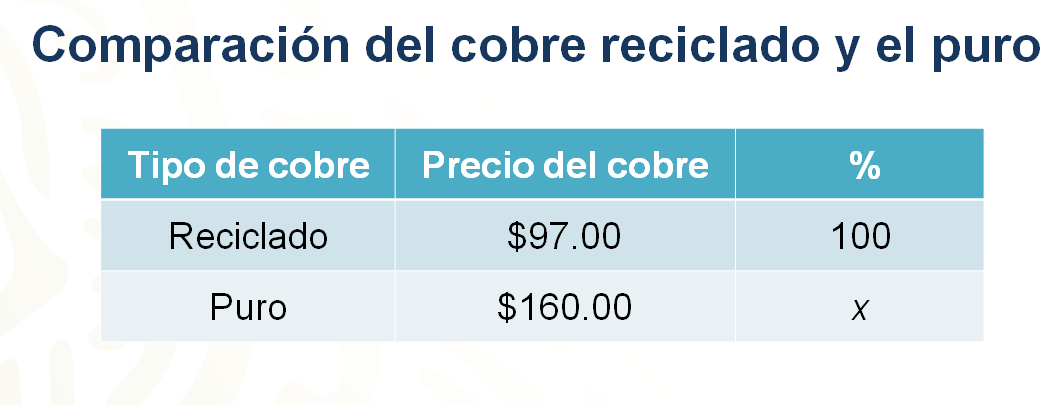
En una columna se colocarán los precios del cobre según su procedencia, si éste es puro o reciclado, y en la otra columna el porcentaje que se le asigna a cada uno. En el caso del cobre reciclado le corresponde un precio de 97 pesos y su porcentaje es de 100% mientras que en el cobre puro su costo es de 160 pesos y el porcentaje que se desconoce se representará con la variable “x”.
Para calcular el porcentaje correspondiente al cobre puro se comparan ambos precios de la siguiente manera, 97 pesos es a 100% como 160 pesos es a “x”.
Al comparar las cantidades, se puede identificar que 160 es mayor que 97 por lo tanto es de esperar que el porcentaje que se obtenga sea mayor que el 100% establecido para 97 pesos.
Existen distintos métodos para obtener un porcentaje. El primer procedimiento que se utilizará se basa en establecer una proporcionalidad entre ambas razones. Por ello se establece la proporcionalidad, de un lado de la igualdad y se tiene la razón de los precios del cobre, 160 sobre 97, y del otro lado, a la razón de los porcentajes, en este caso es “x” sobre 100.
Debes ser muy cauteloso al momento de establecer la igualdad y cuidar que los datos correspondan a la información del problema, porque si inviertes algún dato, el resultado sería incorrecto.
Para conocer la constante, se divide 160 entre 97 lo que da como resultado 1.6494. Esta constante debe ser la misma para la razón de los porcentajes. Por lo tanto, para encontrar el valor de “x” se busca un número que dividido entre 100 dé como resultado 1.6494. Tú en casa puedes ver ¿qué operación permite encontrar este valor?
Una multiplicación es la operación que te permite encontrar el valor faltante. Vas a multiplicar 100 por 1.6494, para facilitar el procedimiento sabes que al multiplicar por alguna potencia de 10 sólo se debe recorrer hacia la derecha el punto decimal tantos lugares como ceros tenga la potencia. En este caso 100 tiene dos ceros por lo que el punto decimal se recorre dos lugares hacia la derecha, obteniendo como resultado 164.94%.

Hay que ver una nueva manera de obtener el resultado. Puedes utilizar la regla de tres, 97 pesos es al 100%, como 160 pesos es a “x” porcentaje, en este caso se plantea la expresión “x” igual a 160 por 100 entre 97; y se tiene que el producto de 160 por 100 es igual a 16 000, y el cociente 16 000 entre 97 es igual a 164.94%, obteniendo el mismo resultado que con el procedimiento anterior.

Pudiste reconocer cómo en ambos procedimientos se realizaron los mismos pasos, pero en diferente orden y el resultado en ambos procedimientos fue el mismo.
¿Cómo se llama esa propiedad que te permitió utilizar estos dos procedimientos sin alterar el resultado?
Es la propiedad conmutativa. Esta es una propiedad de ciertas operaciones que indica que, al cambiar el orden de los términos o factores, el resultado no se altera. Ten presente esto, para que al cierre de esta sesión puedas identificar y comparar cada uno de los procedimientos que se utilizarán durante el transcurso de la lección.
Como puedes ver, al comparar ambos precios, el cobre puro equivale al 164.94% del cobre reciclado. Si se quisiera establecer el porcentaje de ahorro que tienen los artesanos al consumir cobre reciclado, sólo se tiene que restar 164.94% que corresponde al cobre puro menos 100% del cobre reciclado, esto es igual a 64.94%. Lo que significa que el cobre puro es 64.94% más caro que el cobre reciclado, lo que representa un ahorro de dicho porcentaje para cada artesano cuando utiliza este tipo de material.

Con el problema anterior, se pudo calcular qué porcentaje de una cantidad representa otra, en este caso, se logró encontrar el porcentaje de una cantidad mayor respecto a otra, al comparar los precios del cobre.
Dando continuidad a la sesión, se hablará de los artesanos de cobre, para llegar al último paso que recorren estos productos que es la venta.
El costo de una artesanía depende de aspectos importantes como la materia prima, el tiempo que requiere su fabricación, el diseño del producto, entre otras cosas, pero lo más importante es la mano de obra del artesano. Todo esto sumado dará el costo total de cada pieza.
Debes saber también que esta artesanía, al igual que muchas otras de México, es sumamente laboriosa. Existen algunas piezas que pueden tardar desde semanas hasta meses en su fabricación y todo ese tiempo debe ser contemplado dentro del costo del producto.
Revisa un ejemplo de esto, calculando el precio de una artesanía muy particular.
Se trata de un cazo de cobre, el cual es muy útil para preparar diferentes platillos en grandes cantidades, originalmente varios platillos eran preparados en cazos de cobre.

El cazo de cobre fue de las primeras artesanías que el pueblo de Santa Clara del Cobre produjo. Este pueblo, de herencia purépecha, utilizaba en la antigüedad el cobre para generar armas contra la invasión de otras culturas. Fue Vasco de Quiroga quien modificó este oficio para un uso más doméstico.
Se calculará el valor de un cazo de cobre cuya inversión inicial en materia prima es de 1,125 pesos y sumado al tiempo de trabajo y mano de obra, el porcentaje de recuperación para obtener el precio final del producto debe ser de 818%.
¿Cuál sería el precio del cazo tomando en cuenta el porcentaje de recuperación?
Hay que calcular, cómo obtener el precio final del producto de dos maneras diferentes.
Para dar solución a esto debes recordar que el porcentaje se refiere a un tanto de 100, es decir, a una cantidad dada por cada 100, esto se representa en fracción como la cantidad sobre 100 o como decimal, para la artesanía cuyo porcentaje de venta debe ser de 818% se puede expresar como 818 sobre 100, siendo un porcentaje mayor al 100% que se expresa como 818 centésimos, equivalente al número decimal 8.18.
Estas tres, son las diferentes formas en las que se puede representar un porcentaje, siendo su representación como tanto por ciento, como fracción o como número decimal.
Para calcular 818% de 1125, puedes multiplicar 1125 por 8.18 que da como resultado 9 202.50, por lo tanto, el precio final del cazo sería de 9 202.50 pesos.

En este mismo ejemplo se puede aplicar otro procedimiento que previamente has utilizado. Relaciona cada uno de los datos con su correspondiente para, después, comparar las razones de los porcentajes con los precios. Sabes que a 1125 le corresponde el 100% y al costo final, el cual se representa con “x” le corresponde el 818 por ciento.
Al igualar ambas razones se obtiene “x” sobre 1125 que es igual a 818 sobre 100.
Al despejar “x” se obtiene la expresión, “x” igual a 818 por 1125 entre 100.
Multiplicas 818 por 1125, el producto es igual a 920 250, esto dividido entre 100 da como resultado 9 202.50.
Como puedes ver, se obtiene el mismo resultado utilizando ambos procedimientos.

¿Cómo vas hasta aquí? ¿Te han quedado claras las distintas maneras en que puedes utilizar un porcentaje?
Hay que seguir aplicando porcentajes en el mismo contexto de las artesanías de cobre, utilizando los procedimientos que has aprendido.
Una taza de cobre, cuyo valor de inversión en materia prima es de 53.35 pesos, se debe vender al 644% del costo de inversión para lograr solventar todos los gastos de manufactura y comercialización.
¿A qué precio se debería vender la taza?
Como se mencionó al inicio, existen diversos procedimientos que permiten resolver problemas de porcentaje. Primero se relacionan los valores involucrados en el problema, 53.35 pesos le corresponde el 100%, como a la cantidad desconocida “x” le corresponde el 644%.
Para encontrar el costo de la taza se despeja la variable “x”, quedando de la siguiente manera, “x” es igual a 53.35 por 644 entre 100.
¿Puedes reconocer este procedimiento?
Es la regla de 3.
El producto de 53.35 por 644 es igual a 34 357.40, esto divido entre 100 da como resultado 343.57.
Esto quiere decir que el precio de venta de la taza al 644% del costo de la inversión inicial sería de 343.57 pesos, aunque muchos establecimientos suelen redondear a la unidad o decena más cercana para evitar los centavos.

Intenta utilizar algún otro procedimiento de los que has abordado en esta sesión para encontrar la solución de este mismo problema.
A través de los años, las artesanías de Santa Clara del Cobre se han ido modificando para complacer los gustos de los consumidores agregando nuevas técnicas decorativas y desafiando la creatividad del artesano. Una de estas modificaciones es la joyería en cobre, cuyo valor en materia prima puede que sea muy bajo, pero la mano de obra al elaborar estas piezas requiere de un arduo trabajo. Revisa un ejemplo de ello, que te permita aplicar lo que has aprendido a través de la siguiente actividad.
Un artesano desea obtener un 927% del costo de inversión por la venta de unos aretes, a los cuales les ha dedicado bastante tiempo para su elaboración. Piensa utilizar 35% de la ganancia para solventar algunos gastos del taller. El artesano quiere vender los aretes a 115 pesos. Si el costo de la materia prima fue de 14.53 pesos, ¿será correcto dicho precio para cubrir el 927% de recuperación? ¿Cuánto dinero le corresponde al 35% de la ganancia?
Para resolver este problema, debes verificar que los 115 pesos correspondan al 927% que requiere el artesano. Puedes utilizar la representación decimal del 927% para multiplicarlo por el costo de inversión de los aretes, de esta manera puedes comparar ambos precios. La representación decimal de 927% es 927 centésimos expresado como 9.27.
Sabes que el costo de inversión es de 15.43 y para encontrar el precio de venta puedes multiplicar la inversión por el porcentaje de venta. El producto de 14.53 por 9.27 es igual a 134.69. Cuando comparas 115 pesos, que sugiere el artesano, es menor que 134.69 pesos que equivalen al porcentaje de venta. Por lo que dicho precio estaría por debajo del porcentaje de recuperación esperado.

Otro método que puedes utilizar, es obtener qué porcentaje de 14.53 pesos de la inversión inicial representan los 115 pesos del posible precio de venta, para ello se representa la información en la siguiente tabla.

En la primera columna se colocan los precios en pesos, 14.53 y 115, mientras que en la segunda columna se pone el porcentaje que le corresponde a cada precio, a 14.53 le corresponde el 100%, mientras que el porcentaje de 115 se representa con “x” debido a que es el valor que se desconoce.
Aplicando la regla de tres, “x” es igual al producto de 115 por 100 entre 14.53.
El producto de 115 por 100 es igual a 11 500, al dividir esta cantidad entre 14.53 te da como resultado 791.46.
Por lo tanto, el porcentaje de 14.53 pesos, que representan 115 pesos, es de 791.46% el cual es menor que el 927%.
Se realizaron dos procedimientos distintos que te dieron datos diferentes del mismo problema, pero ambos te permiten dar respuesta a la primera pregunta planteada en el problema la cual decía “¿Será correcto dicho precio para cubrir el 927% de recuperación?”
Al utilizar el primer procedimiento se obtuvo el precio que le corresponde al 927%, mientras que el segundo te permite conocer el porcentaje del precio asignado a los aretes por el artesano. Con ambos resultados puedes llegar a la misma conclusión, en la que el precio establecido por el artesano no sería suficiente para cubrir el porcentaje de recuperación que requiere. Y como viste, para obtener dicho porcentaje de recuperación, el precio de los aretes tendría que ser de 134.69 pesos.
Por último, hace falta calcular la cantidad que corresponde al 35% de la ganancia. Lo que se hará considerando el precio que corresponde al 927% de 14.53 pesos, es decir, 134.69 pesos.
Para calcular la ganancia neta debes descontar el monto de la inversión al precio final, es decir restarás 134.69 menos 14.53 = 120.16, lo que representa el total de la ganancia de ese producto.
El artesano invertirá el 35% de su ganancia nuevamente en el taller, para calcular la cantidad que aportará tomas a 120.16 como el 100% y calcularás a cuanto corresponde el 35%, “x” representará la cantidad en pesos que no conoces.
Para este problema nuevamente planteas tu relación de proporcionalidad, igualarás la razón de los datos donde “x” sobre 120.16 es igual a 35 sobre 100.
Despejas “x” para aplicar la ya conocida regla de 3 y multiplicas 35 por 120.16, que es igual a 4 205.6, al dividirlo entre 100 obtienes como resultado final 42.05.
Quiere decir que, de la venta de los aretes, el artesano debe reinvertir 42.05 pesos en el taller.

¿Qué otros procedimientos hubieras utilizado para llegar a este mismo resultado?
Se te propone realizar tus procedimientos y anotaciones para que puedas compartirlos con tu maestra o maestro a la distancia.
Ahora se te invita a que reflexiones sobre lo que viste en esta sesión.
Aprendiste a representar de distintas maneras un porcentaje, como fracción o decimal. Cada una de estas representaciones te permiten utilizar un procedimiento distinto para calcular porcentajes.
Ahora, ¿podrías identificar y relacionar en que procedimientos se utiliza cada una de las siguientes representaciones?

A continuación, verás los tres procedimientos que se utilizaron durante esta sesión, cada uno de ellos se encuentra en un recuadro de distinto color.
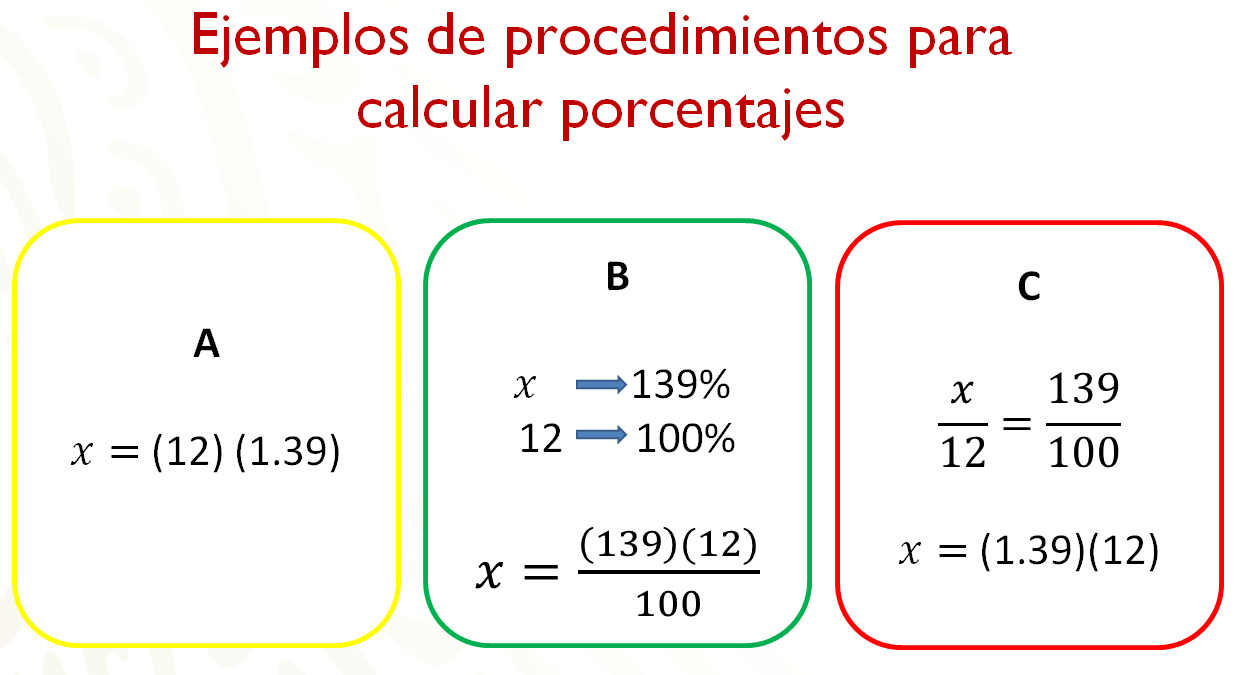
En el recuadro con la letra “a” se están multiplicando dos factores para conocer cierto porcentaje de una cantidad, representado por “x”, uno de los factores es la representación decimal de un porcentaje y el otro la cantidad de la que se quiere obtener el porcentaje.
En el recuadro “b” se representa el procedimiento correspondiente a una regla de tres; observa con detenimiento cómo se multiplican los factores cuyos datos no tienen relación directa y se divide entre un tercer número.
En el recuadro “c” observas la relación de proporcionalidad, donde se iguala dos razones, cuyo cociente es la constante de proporcionalidad, este cociente será multiplicado por el tercer dato.
Como puedes observar, el procedimiento mostrado en el recuadro “B” corresponde a la representación de un porcentaje, como tanto por ciento, el recuadro “C” dicha representación se hace como fracción, y finalmente, en el recuadro “A” la representación del porcentaje es como número decimal.
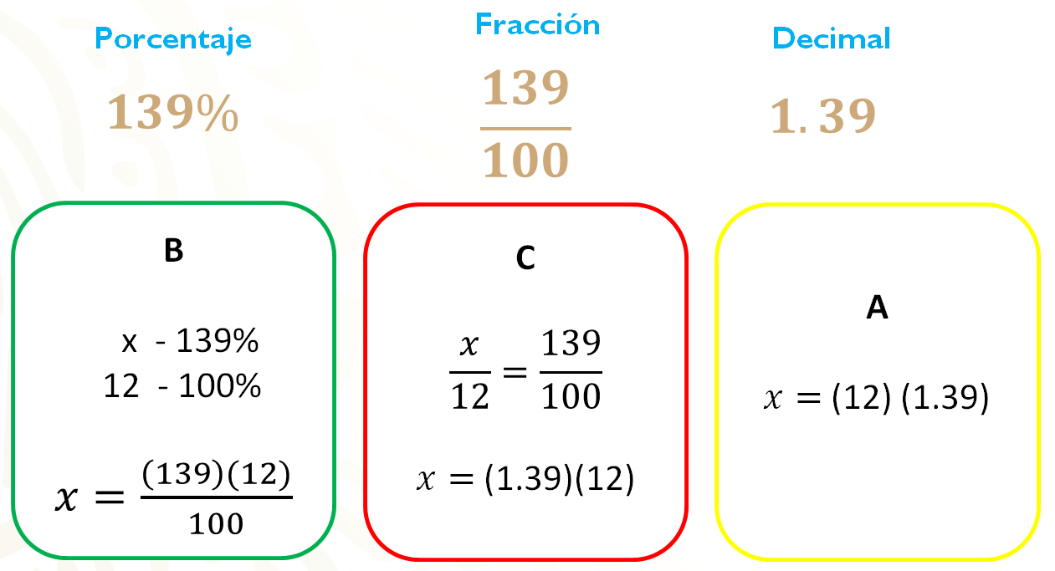
- ¿Qué similitudes encuentras en cada uno de los procedimientos?
- ¿Lograste identificar que en los procedimientos las operaciones predominantes al calcular los porcentajes de una cantidad o viceversa, son la multiplicación y la división?
Debido a que se utilizan razones para igualar la proporción entre 4 datos. Lo común es que se utilicen estos dos algoritmos para encontrar la solución del valor faltante.
En casa, puedes comprobar que el resultado de los tres procedimientos efectivamente sea el mismo.
Ahora que ya conoces el valor en porcentajes que requiere una artesanía mexicana, podrás valorar todo el trabajo y tiempo invertido a ese producto y a pagarlo al precio justo.
El reto de hoy:
Concluye las actividades que se te pidieron en el desarrollo de la sesión.
El primero relacionado con la venta de los aretes, en el cual se te pregunta: ¿Qué otros procedimientos hubieras utilizado para llegar al mismo resultado presentado? Y en donde se te propone realizar tus procedimientos y anotaciones para que puedas compartirlos con tu maestra o maestro a la distancia.
Y el segundo, en el cual se te pide comprobar que el resultado de los tres procedimientos del último ejercicio que revisaste efectivamente sea el mismo.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas