Cálculo de porcentajes
Cálculo de porcentajes
Aprendizaje esperado: resuelve problemas de cálculo de porcentajes, de tanto por ciento y de la cantidad base.
Énfasis: resolver problemas de cálculo de porcentajes.
¿Qué vamos a aprender?
Resolverás problemas de cálculo de porcentajes. en donde, vas a calcular la cantidad final, después de aplicar cierto porcentaje de descuento; y también determinarás el porcentaje que representa una cantidad de otra.
¿Qué hacemos?
Para iniciar, es importante que recuerdes, que el significado del porcentaje está asociado a una cantidad dada como una parte de 100, que significa “de cada cien”. También se le llama tanto por ciento, donde “por ciento” significa -de cada cien unidades- es decir, es una cantidad que corresponde proporcionalmente a una parte de cien.
Quizás hayas observado que, en muchos comercios como tiendas de ropa, de calzado e incluso en los mercados, ofrecen ofertas a sus productos que van desde el 10 por ciento hasta el 70 por ciento de descuento, sobre su precio.
Analiza la información del siguiente video entre los minutos 0:21 a 1:42
- Porcentajes.
https://www.youtube.com/watch?v=PGwLoqZsmcM
Tal y como se mencionó en el video, el porcentaje se denota utilizando el símbolo “por ciento”, que consta de dos ceros separados con una diagonal, y que se debe escribir después del número al que se refiere.

Por ejemplo: treinta y dos por ciento se representa mediante 32 y el símbolo de porcentaje y significa ‘treinta y dos de cada cien’.
También puede representarse de la siguiente manera:
Treinta y dos por ciento representa 32 de cada 100 unidades.
Por lo que, como fracción, puedes representarlo como 32 centésimos y como número decimal es igual a cero punto 32
Entonces, para obtener el porcentaje de una cantidad, por ejemplo 32 por ciento, se multiplica la cantidad por el porcentaje, representado como número decimal, en este caso por cero punto 32
Por ejemplo, 32 por ciento de 2 000 significa la parte proporcional a 32 unidades de cada 100 de esas 2 000 unidades; es decir: treinta y dos por ciento de dos mil es igual a cero punto treinta y dos por dos mil, igual a seiscientos cuarenta.

Con estos elementos ya puedes dar sentido y significado a la resolución de problemas en los que tengas que calcular el porcentaje de descuento para obtener el precio final que se paga por productos que tienen alguna rebaja, mercancía que vas a comprar en algún comercio o para ver los descuentos realizados a determinados productos o servicios, entre otras situaciones.
Ahora analiza el siguiente problema de porcentajes:
Hace unos días, Lesli fue a una tienda en donde encontró ciertas prendas de vestir, con diferentes porcentajes de descuento y compro algunas de ellas.
Los productos que compro fueron unas botas que costaban 860 pesos, pero tenían 20 por ciento de descuento, un pantalón de 700 pesos con 35 por ciento de descuento y una gorra de 240 pesos con 5 por ciento de descuento.
Con relación al problema, responde las siguientes preguntas:
- ¿Cuánto pago por cada artículo considerando el descuento?
- ¿Cuál fue el costo total de la compra?

¿Ya sabes qué operaciones realizar para responder las preguntas?
Analiza la situación.
Primero, hay que organizar la información en una tabla. En la primera columna se registra el nombre de los productos; en la segunda, el precio inicial; en la tercera columna, los porcentajes de descuento y en la cuarta y quinta columna, la información que se tiene que calcular; es decir, la cantidad a descontar y el precio final, respectivamente.
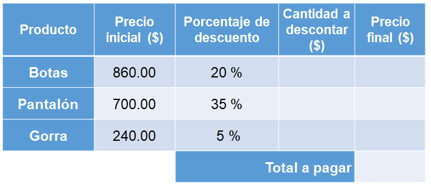
Se calcula el costo de las botas, para ello se representa el 20 por ciento como fracción, quedando como 20 centésimos, y al convertirlo a número decimal el resultado es 0.20 que es igual a 0.2. Entonces, 20 por ciento de 860 es igual a 860 por 0.2, que es igual a 172 pesos. Esa es la cantidad para descontar y la cual se restará al precio inicial para obtener el costo final de las botas; entonces: 860 menos 172 es igual a 688. Eso significa que por las botas de 860 pesos con el 20 por ciento de descuento se pagan 688 pesos.
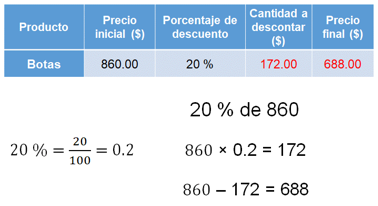
Ahora se calculará el costo final del pantalón que tiene un precio de 700 pesos y un descuento de 35 por ciento. Como sabes, 35 por ciento es igual a 35/100, que, al dividir numerador entre denominador, se obtiene el valor de 0.35; entonces, 35 por ciento de 700 es igual a 700 por 0.35, que da como resultado 238.
Siendo 238 pesos el valor correspondiente al 35 por ciento de 700 pesos. Ahora, a 700 pesos se le resta 238 pesos, esto es igual a 462 pesos, lo cual representa el costo final del pantalón con 35 por ciento de descuento.
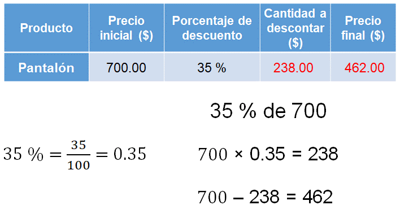
Hay que calcular el costo de la gorra.
Por lo que respecta al costo de la gorra que es de 240 pesos, tiene un descuento del 5 por ciento, entonces hay que expresarlo en su fracción decimal correspondiente, la cual es cinco sobre cien y, usando la expansión decimal, se divide 5 entre 100 para obtener 0.05; se multiplica dicha cantidad por 240 pesos, que es el costo de la gorra, y se obtienen 12 pesos. Ésta es la cantidad que se resta del costo inicial; entonces: 240 menos 12 es igual a 228 pesos, que es el costo final de la gorra.

Ahora, hay que obtener el total que pago Leslie.
Considerando la tabla que se planteó al principio de este problema, ya con los datos encontrados, en la columna final se suma el precio final de las prendas: 688 más 462 más 228 es igual a 1 378. Con esto, ya sabes que Leslie pagó 1 378 pesos por su compra.
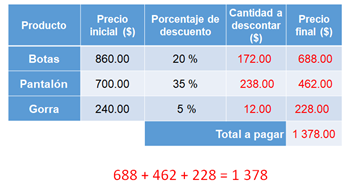
Con el problema anterior, aprendiste a calcular el porcentaje de una cantidad y la cantidad final para obtener el porcentaje de descuento. Una manera muy útil para conocer la cantidad final, cuando se aplica un porcentaje de descuento, es calcular directamente el número final considerando el porcentaje que representa de la cantidad inicial.
Por ejemplo, Leslie compró unas botas que tenían 20 por ciento de descuento. ¿Qué porcentaje del precio original pagó por las botas?
Como el precio inicial de las botas representa el 100 por ciento y le descontaron 20 por ciento, entonces pagó: 100 por ciento menos 20 por ciento, que es igual a 80 por ciento del precio inicial.
Entonces lo que tienes que hacer es multiplicar el precio inicial por el porcentaje que se paga de la prenda; es decir, 860 por 0.8 que es igual a 688 pesos.
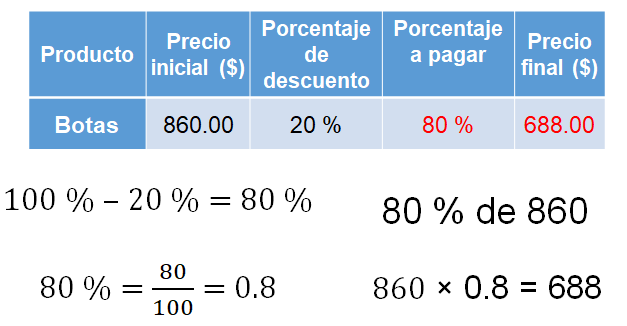
Ésta es una buena manera de calcular la cantidad final al aplicar un porcentaje de descuento.
Revisa el siguiente video a partir del segundo 0:35 al minuto 2:10. en donde se plantea una situación en la que se debe calcular el porcentaje que representa una cantidad de otra.
- “¿Qué tanto por ciento es?”
https://www.youtube.com/watch?v=vVKNIxlvBjM&list=PL1xdpLgBMQFXuj0l
Como acabas de observar, en el video anterior, se calculó que porcentaje representa una cantidad de otra, para saber qué porcentaje de la población mexicana tenía, en 2015, entre 0 y 14 años.
Ahora, analiza lo siguiente. Toma nota de la información.
Al calcular porcentajes intervienen 4 variables: cantidad total o base, cantidad parcial, 100 por ciento y porcentaje parcial, que se relacionan de la siguiente manera: cantidad total es 100 por ciento, como cantidad parcial es a porcentaje parcial.

Esta relación permite encontrar cualquier valor desconocido, a partir de las otras tres variables. Por ejemplo: ¿qué porcentaje de 80 representa 25?
Aplicando la relación anterior, entonces la cantidad total 80 es a 100 por ciento como la cantidad parcial, 25, es a porcentaje parcial equis. Para saber qué porcentaje representa equis se multiplica 25 por 100 entre 80, cuyo resultado es igual a 31.25 por ciento. Esto quiere decir que 25 representa el 31.25 por ciento de 80

Lo anterior se demuestra al multiplicar 80 por 31.25 %, 80 por 0.3125 es igual a 25
Otra manera de calcular lo anterior es relacionando las cuatro variables de la siguiente manera: cantidad total es la cantidad parcial como 100 por ciento es a porcentaje parcial. Entonces, se divide la cantidad parcial, 25, entre cantidad total, 80, y se multiplica el resultado por 100 para corroborar que 25 representa el 31.25 por ciento de 80

Ahora, hay que retomar el problema del censo de población del INEGI.
El censo de población y vivienda que realizó el INEGI en 2020, en México, registró 127 millones 900 mil habitantes, de los cuales 30 millones 696 mil tenían entre 15 y 29 años. La pregunta es: ¿qué porcentaje de la población representaba a las personas en este rango de edad?

Retomando la información y lo que aprendiste, para calcular el porcentaje que representa una cantidad de otra, ahora se considerará contar con el apoyo de una calculadora, para así determinar qué porcentaje de la población representaban los jóvenes de entre 15 y 29 años. Para ello, se divide la población de jóvenes entre la población total y se multiplicará el resultado por 100; es decir, 30 millones 696 mil entre 127 millones 900 mil por 100
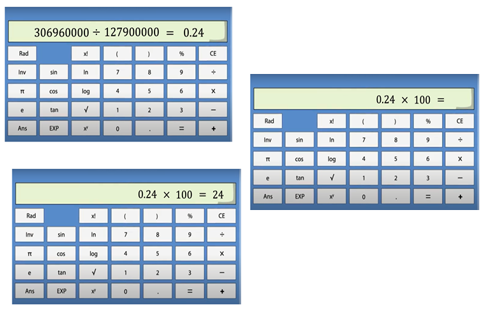
Al resolver la división 30 millones 696 mil entre 127 millones 900 mil, se obtiene como resultado 0.24; y al multiplicar 0.24 por 100 el resultado es 24.
Con esto, sabes que la población mexicana entre 15 y 29 años en 2020 representaba el 24 por ciento de la población total.
Considerando el procedimiento aprendido, hay que elaborar las operaciones de manera escrita y representar la información en una gráfica circular.
Entonces, se divide 30 millones 696 mil entre 127 millones 900 mil, lo cual es igual a 0.24 y esta cantidad se multiplica por 100, dando como resultado 24 por ciento que, como ya se vio, representa a la población entre 15 y 29 años en el país.
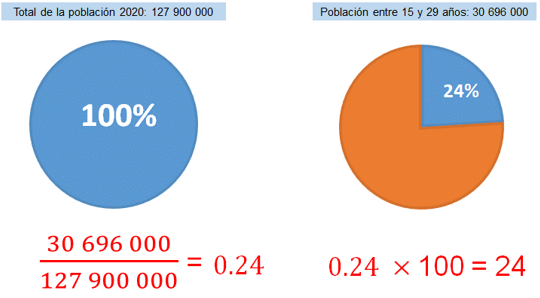
Pero hay que comentar que no sólo en el plano de la estadística se puede emplear el cálculo del porcentaje que representa una cantidad de otra. En asuntos más cercanos a la vida cotidiana también se puede hacer este tipo de cálculos, como en el siguiente caso. Toma nota de la información para que resuelvas la siguiente actividad.
En un terreno, cuya área total es de 4 000 metros cuadrados, se quieren destinar 400 metros cuadrados para la realización de un “huerto casero”. Otra parte del terreno, que mide 1 600 metros cuadrados, lo quieren utilizar para siembra de maíz y los 2 000 metros cuadrados restantes para actividades relacionadas con la floricultura.
Se requiere saber qué porcentaje del terreno representa cada sector para destinar un presupuesto proporcional a la medida de cada espacio.
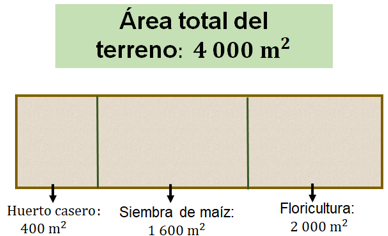
Considerando el orden de los datos en el problema, se empieza por calcular el porcentaje del terreno que representa el “huerto casero”.
Primero, se relacionan los valores involucrados: 400 metros cuadrados es a equis por ciento, como 4 000 metros cuadrados es a 100 por ciento.
Se divide 400 entre 4 000, en este caso se va a reducir la expresión dividiendo entre 400 ambos miembros, lo cual da 4 entre 40 y se vuelve a reducir, ahora dividiendo entre 4 para obtener 1 entre 10. Al dividir da 0.1, el cual se multiplica por 100. El resultado final es 10 por ciento; es decir, la parte destinada al “huerto casero” representa 10% del terreno.

Una vez que has visto el método empleado, ahora hay que saber qué porcentaje del terreno representa la superficie dedicada a la siembra del maíz.
Primero, se relacionan los valores involucrados. Sabes que el área para la siembra del maíz es de 1 600 metros cuadrados; se divide 1 600 entre 4 000, pero se simplifica el numerador en el denominador hasta obtener 4 entre 10 y, al dividir, se obtiene 0.4; se multiplica por 100 por ciento y se obtiene el resultado de 40 por ciento.

Sólo resta la última parte del terreno: la que corresponde a la floricultura y en la que destinarán 2 000 metros cuadrados. Pero, ese procedimiento se dejará que tú lo realices como reto de esta sesión.
A continuación, se realizará un recuento de lo revisado en el tema de este día.
Durante esta lección aprendiste a resolver problemas que implican calcular el porcentaje de descuento de alguna mercancía. Se requiere convertir el porcentaje a un valor decimal y multiplicar por el costo del producto que representa el 100 por ciento de la cantidad a la que le quieres quitar el valor de dicha rebaja.
Por otra parte, revisaste el proceso para determinar el porcentaje que representa una cantidad de otra; para esto, se procedió a dividir la cantidad menor entre la cantidad mayor y su resultado se multiplicó por el 100 por ciento, lo cual da el porcentaje que se está buscando.
Recuerda algunos de los usos de los porcentajes:
- Relacionar una parte con el todo, por ejemplo: “58 por ciento de los aspirantes a ingresar a la universidad son mujeres”.
- Determinar una proporción entre dos cantidades, como en el caso de la proporción de levadura y harina para elaborar un pastel, “la cantidad de levadura representa 30 por ciento de la cantidad de harina”.
- Describir a la población indicando el margen relativo de una magnitud sobre ella. Utilizando este ejemplo: “60 por ciento de la población de México tiene estudios superiores”.
Como viste, gran parte de la estadística se expresa en porcentajes. Así se ha demostrado que, con los casos anteriores, los porcentajes tienen importancia, incluso en otras ciencias, como en el caso de la química, en la que se requiere saber la concentración porcentual de los componentes en una sustancia.
Con todo esto, se puede concluir entonces que: los porcentajes son necesarios en la vida cotidiana, así como en cualquier rama de la ciencia.
Has concluido el tema del día de hoy.
El reto del hoy:
Realiza el ejercicio que se te solicitó en el desarrollo de la sesión, relacionado con resolver la problemática de la última parte del terreno: la que corresponde a la floricultura y en la que se destinarán 2 000 metros cuadrados.
No olvides en la medida de tus posibilidades, buscar o contactar a tu maestra o maestro para compartir tus respuestas, y en tu libro de Matemáticas de primer grado ubica este tema y resuelve los problemas o ejercicios relacionados con el tema, para practicar.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas