Área y volumen
Área y volumen
Aprendizaje Esperado: consolidar contenidos del eje: forma, espacio y medida.
Énfasis: integrar los contenidos del tema: magnitudes y medidas.
¿Qué vamos a aprender?
En esta sesión trabajarás con dos temas de geometría: en el primer tema, calcularás el área de triángulos y cuadriláteros; el segundo está relacionado con el espacio que ocupa un cuerpo geométrico y con su capacidad; es decir el volumen, el cual aplicarás en diferentes prismas rectos.
Se te recomienda que para el desempeño de tus actividades tengas a la mano tu cuaderno u hojas reutilizables, lápiz, goma, sacapuntas y regla. Así como tu libro de texto de la asignatura. En caso de tener una discapacidad visual, prepara hojas ledger, un punzón y una regleta.
¿Qué vamos a hacer?
Para iniciar, se definirá lo que es el área.
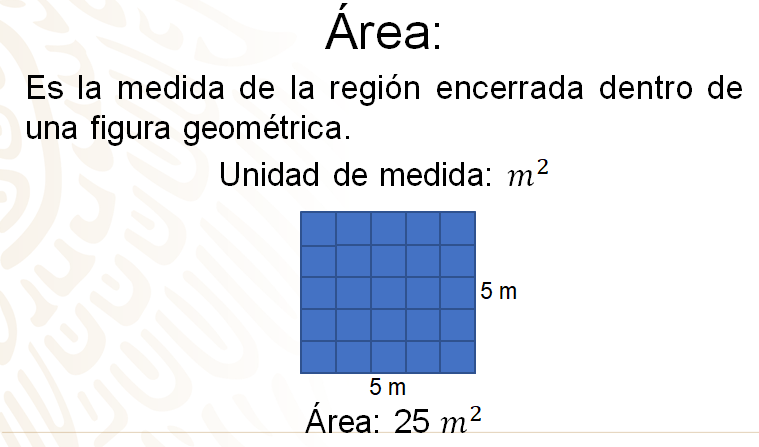
Como sabes, el área es la medida de la región encerrada dentro de una figura geométrica. Ésta se mide en unidades cuadradas; es decir, si se tiene una figura que tenga un área de 25 metros cuadrados, esto significa que dentro de esta figura caben 25 cuadrados de 1 metro por lado.
En esta sesión, revisarás el área de cuatro figuras geométricas que son: el rectángulo, el cuadrado, rombo y el triángulo.
La unidad de medida principal para calcular áreas es el metro cuadrado. ¿Tú en casa, recuerdas cuál es la fórmula para obtener el área de un rectángulo?
La fórmula para obtener el área del rectángulo es: área es igual a la base por la altura, donde la letra “b” representa la medida de la base del rectángulo y la letra “h” representa a la medida de la altura. Es muy importante destacar que la base y la altura siempre deben estar en la misma unidad de medida.
Para encontrar el área de un cuadrado se debe aplicar la siguiente fórmula: área es igual a lado por lado. Hay que mencionar que esta figura es un caso especial del rectángulo, debido a que la base mide lo mismo que la altura. El rectángulo y el cuadrado son cuadriláteros; es decir, son polígonos que cuentan con cuatro lados. Pon atención y toma nota de la información más relevante.

Por las características del cuadrado y del rectángulo, estas figuras pertenecen a la familia de los paralelogramos, ya que sus lados son paralelos dos a dos; por ejemplo, el cuadrado cuenta con 4 lados iguales y 4 ángulos rectos, el rectángulo tiene lados iguales dos a dos y 4 ángulos rectos.
¿Conoces alguna otra figura que tenga características similares a las figuras antes mencionadas?
¡El rombo! Ya que también cuenta con cuatro lados iguales, pero, a diferencia del cuadrado, el rombo cuenta con ángulos iguales dos a dos.
Para obtener el área del rombo se utilizará la siguiente fórmula: área es igual al producto de sus diagonales dividido entre dos; es decir, diagonal mayor, por diagonal menor, entre dos. La letra “D” mayúscula representa la diagonal mayor y la letra “d” minúscula representa a la diagonal menor.

Hasta el momento, ya conoces la fórmula para obtener el área de tres figuras:
| La del cuadrado es: | Área es igual a lado por lado. |
| La del rectángulo: | Área es igual a la base por la altura. |
| La del rombo: | Área es igual al producto de la diagonal mayor por la diagonal menor, entre dos. |
Sólo falta conocer la fórmula para obtener el área de un triángulo. Tú en casa, ¿ya sabes cuál es la fórmula?
Base por altura entre dos. Esta fórmula se obtiene al trazar una diagonal en un rectángulo formándose, así, dos triángulos congruentes; es decir, iguales; por lo que el área de un triángulo se puede calcular como la mitad del área de un rectángulo.

Ahora, hay que analizar la siguiente situación:
Don Miguel trabaja en una vidriera. Hace unos días, un cliente, le solicitó realizar 40 piezas de espejos cuadrados, para colocarlos en su sala. Para no equivocarse al realizar los cortes, don Miguel primero hizo un boceto; es decir, un esquema en papel, para después replicarlo en el vidrio. A don Miguel no le han surtido más hojas de vidrio y solamente cuenta con una hoja de vidrio, que tiene una medida estándar de 1.80 metros de altura por 2.60 metros de base.
Se te sugiere anotar las siguientes preguntas para reflexionar:
- ¿Cuántas hojas de vidrio necesitará don Miguel para realizar las 40 piezas de espejos?
- ¿Cuál será el área de cada uno de los espejos?
Ahora observa la siguiente imagen:
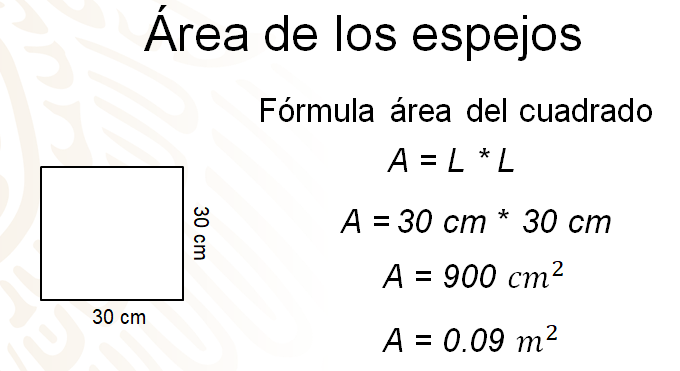
Como puedes observar en la figura, el cuadrado tiene sus cuatro lados iguales, con una medida de 30 cm por lado, como lo solicitó el cliente.
Con esta información, ya se puede dar respuesta a la segunda pregunta: ¿Cuál será el área de cada uno de los espejos?
La fórmula que se utilizará es: área es igual a lado por lado. Si cada lado del espejo mide 30 centímetros, debes sustituir este valor en la fórmula; por lo que el área es igual a 30 cm por 30 cm, dándote como resultado 900 centímetros cuadrados, que en metros cuadrados serían 0.09.
Con esta información, ya puedes darle respuesta a la primera pregunta: ¿Cuántas hojas de vidrio necesitará Don Miguel para realizar las 40 piezas de espejos?
Si la medida de la hoja de vidrio es de 1.80 metros de altura por 2.60 metros de base, ¿qué figura forma la hoja de vidrio con estas medidas?
¡Un rectángulo! Se te sugiere pongas atención al siguiente procedimiento.
Para darle respuesta a la primera pregunta, debes de obtener el área de la hoja de vidrio; para ello ¿qué fórmula utilizarías?
Área es igual a base por altura. Después sustituyes los valores en la fórmula. El valor de la base, en este caso, es de 2.60 m y de la altura 1.80 m; por lo que el área es igual a 4.68 metros cuadrados.
Si a don Miguel le solicitaron 40 piezas, el área que se ocupará de la hoja de vidrio será de 3.60 metros cuadrados; ya que cada vidrio tiene un área de 0.09 metros cuadrados; por lo que se puede decir que, con una sola hoja, podrá realizar las 40 piezas que le solicitó su cliente.

En esta situación, pudiste observar cuál es la aplicación de las fórmulas para obtener el área del cuadrado y del rectángulo.
Ahora, analiza el siguiente caso.
Sofía es una estudiante de secundaria y le pidieron que construyera un papalote en forma de rombo en una cartulina de color rosa y que utilizara las siguientes medidas para su construcción: su diagonal mayor deberá medir 50 cm y su diagonal menor será de 30 cm. La pregunta es: ¿Cuál es el área del papalote?
El área es igual a la diagonal mayor, por la diagonal menor, entre dos. Ahora, se sustituyen las medidas que se le proporcionaron a Sofía para la construcción de su papalote: la diagonal mayor mide 50 cm, la diagonal menor mide 30 cm y su producto es de 1,500 centímetros cuadrados. Para obtener el área del rombo ¿qué falta realizar?
Faltaría hacer la división entre dos; por lo que 1,500 centímetros cuadrados entre dos, es igual a 750 centímetros cuadrados.

Hasta el momento, has analizado cómo aplicar las fórmulas para calcular el área del cuadrado, rectángulo y del rombo en diversas situaciones.
Ahora, analizarás el siguiente caso: Ana y Fernando construyeron banderines con forma triangular para el grupo de animación de su escuela. Cada quien hizo uno.
Las medidas de los banderines de cada uno de ellos son las siguientes:
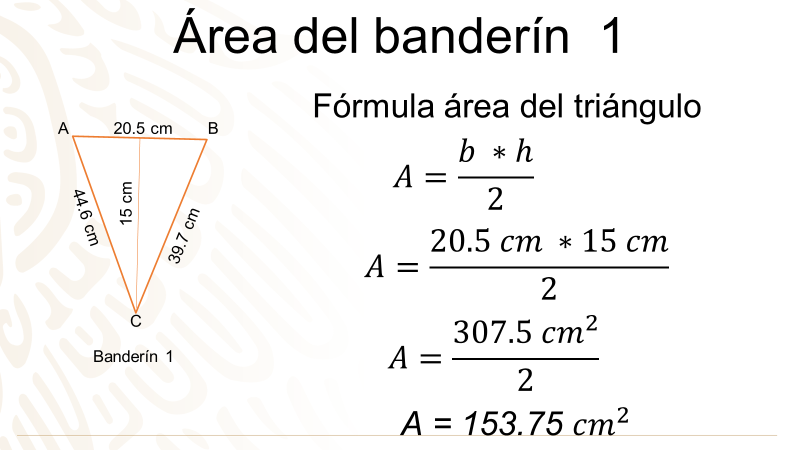
Banderín 1, lo realizó Fernando con las medidas: 44.6 cm, 20.5 cm, 39.7 cm y una altura de 15 cm.
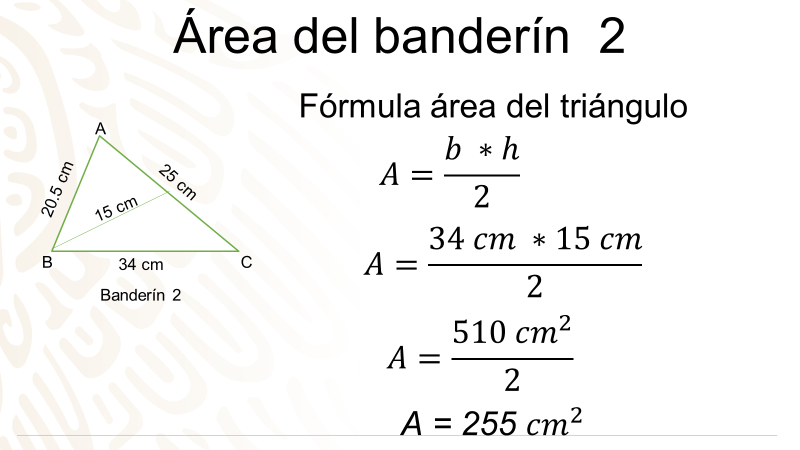
Banderín 2, lo realizó Ana con las medidas: 20.5 cm, 34 cm, 25 cm y una altura de 15 cm.
De acuerdo con los datos mostrados, ¿puedes establecer si los banderines tienen la misma área, si ambos cuentan con la misma altura?
Como tú sabes, la altura de un triángulo es el segmento de recta perpendicular a cualquiera de los lados del triángulo.
Ahora hay que encontrar el área de los banderines.
La fórmula que utilizarás es: área es igual a base por altura, entre dos. Del primer banderín, la base mide 20.5 cm y su altura es de 15 cm; por lo que, al efectuar el producto, te da como resultado 307.5 centímetros cuadrados. Ahora, realiza la división entre dos; de modo que el área del primer banderín es de 153.75 centímetros cuadrados.
Después, hay que encontrar el área del segundo banderín que tiene como base 34 cm y de altura 15 cm. Al efectuar el producto te da como resultado 510 centímetros cuadrados. Ahora hay que realizar la división entre dos. El área del segundo banderín es de 255 centímetros cuadrados, por lo que los banderines de Ana y Fernando no tienen la misma área, a pesar de tener la misma altura.
Ya has analizado cómo aplicar las fórmulas para calcular el área del cuadrado, rectángulo, rombo y del triángulo, en diversas situaciones.
A continuación, se explicará qué es el volumen.
El volumen es el espacio que ocupa un cuerpo geométrico. Éste se mide en unidades cúbicas y la unidad básica del volumen es el metro cúbico. Los prismas que analizarás en esta sesión son los prismas rectos. Estos prismas tienen dos bases poligonales congruentes que son paralelas entre sí, además de que tienen una altura o profundidad.
Dependiendo de la forma de su base, reciben su nombre; por ejemplo, si sus dos bases tienen forma de un triángulo, se llama prisma triangular; si sus dos bases tienen forma de un cuadrado, se llama prisma cuadrangular y así sucesivamente.

Los prismas cuentan con aristas, que son los segmentos de recta que limitan las caras de un cuerpo geométrico. También analizarás la relación que existe entre la capacidad y el volumen.
La capacidad es el espacio vacío que tiene un objeto para contener a otra u otras cosas dentro de éste; a diferencia del volumen, que es el espacio que ocupa un cuerpo. Es por ello que entre ambos conceptos existe una relación de equivalencia, que está basada entre el litro, que es una unidad de capacidad y el decímetro cúbico, que es una unidad de volumen.
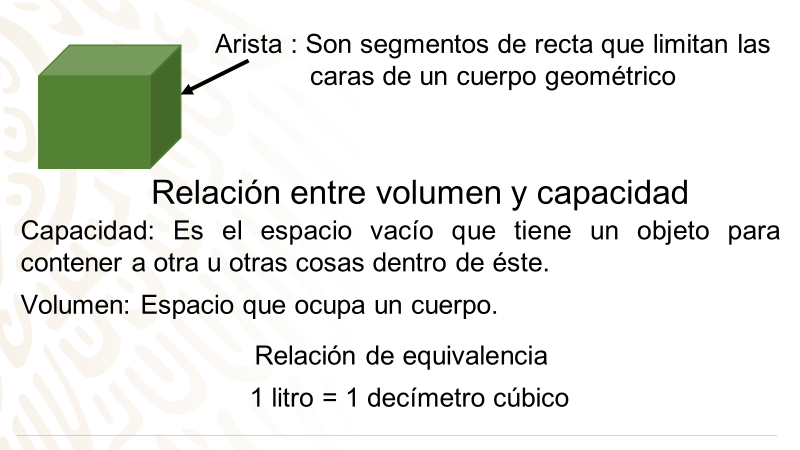
Los cuerpos geométricos que analizarás son:
| El cubo: | El cual cuenta con seis caras cuadradas. |
| El prisma rectangular: | Que está limitado por dos rectángulos paralelos e iguales, llamados bases y cuatro caras rectangulares. |
| El prisma triangular: | Que está limitado por dos triángulos paralelos e iguales como bases y tres caras rectangulares. |
Para obtener el volumen de cualquier prisma recto debes aplicar la siguiente fórmula: volumen es igual al área de la base, por la altura.
Ahora, vas a analizar la siguiente situación. Por favor, toma nota de la información más relevante.
Paco es un muchacho que se dedica a trabajar como albañil. En estos días, le han encargado que construya una pileta —en algunos lugares la conocen como pila de agua, tanque o cisterna—, utilizando tabiques y cemento, en una casa cercana a su domicilio. El cliente le encargó este trabajo con la finalidad de abastecer agua a toda su familia. El cliente de Paco le solicitó que realizara la pileta con las siguientes dimensiones: 2.5 metros de largo, 1.8 metros de ancho y, de altura, 3 metros.
¿Cuántos litros de agua se necesitarán para llenar la pileta? ¿Qué forma tendrá? ¿Cuál será su volumen?
Se te sugiere que repliques en tu cuaderno, o en hojas reutilizables, el esquema de la pileta que se presentará a continuación.
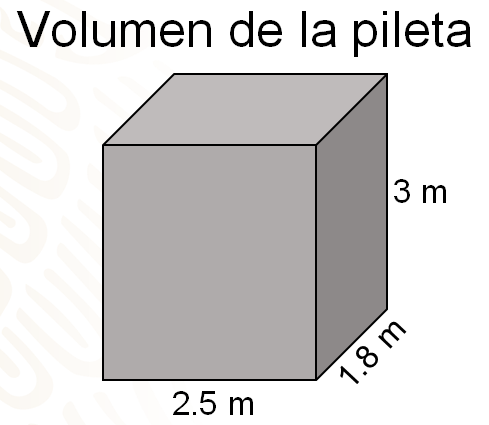
Como puedes ver, la pileta tiene las siguientes dimensiones: 2.5 metros de largo, 1.8 metros de ancho y de profundidad 3 metros. Su contorno es de color gris con forma de un rectángulo.
¿Qué forma tiene la pileta?
Se trata de un prisma rectangular. Con esta información, ya puedes darle respuesta a la tercera pregunta: ¿Cuál será el volumen de la pileta?
Pon atención al siguiente procedimiento y toma nota de la información más relevante.
Para calcular el volumen de un prisma recto, debes utilizar la siguiente fórmula: Volumen = Área de la base por altura.
Con esta información, podrás calcular el volumen de la pileta. Primero, obtendrás el área de la base; es decir, encontrarás el área del rectángulo. La fórmula para calcular el área del rectángulo es: base por altura, como ya lo viste anteriormente. Ten cuidado de no confundir la altura de la base con la altura del prisma. Después multiplicarás 2.5 metros, por 1.8 metros, cuyo producto es 4.5 metros cuadrados.
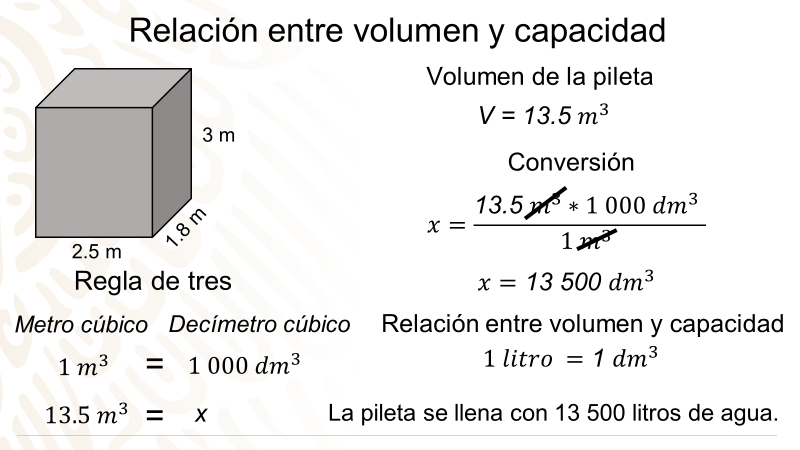
Ahora, encontrarás el volumen, multiplicando el área de la base por la altura de la pileta, que es 3 metros; de este modo, tienes que 4.5 metros cuadrados por 3 metros, te da como resultado 13.5 metros cúbicos.

Ya se encontró el volumen de la pileta que es de 13.5 metros cúbicos. Tú en casa, ¿ya sabes cuántos litros de agua se necesitarán para llenar la pileta?
Como se mencionó anteriormente, existe una relación entre el litro, que es una unidad de capacidad, con el decímetro cubico, que es una unidad de volumen. Ya sabes que 1 litro es igual a 1 decímetro cúbico, pero el volumen que se calculó de la pileta está en metros cúbicos.
Así que, se tiene que realizar la conversión de metros cúbicos a decímetros cúbicos; para ello, se debe realizar una regla de tres: debes multiplicar 13.5 metros cúbicos por 1000 decímetros cúbicos y dividir entre 1 metro cúbico.
Cuando tienes la misma unidad de medida en el numerador y en el denominador, puedes simplificarlas, ya que el numerador está multiplicando y en el denominador dividiendo. Siendo estas operaciones inversas, sólo quedan los decímetros cúbicos. Ahora, efectúas el producto 13.5 por 1000, que es igual a 13,500 entre uno, lo que te da como resultado 13,500 decímetros cúbicos; por lo tanto, si ya sabes que un decímetro cúbico tiene una capacidad de un litro, puedes asegurar que la pileta se llena con 13,500 litros de agua.
A los prismas rectangulares también se les conoce como paralelepípedos. Ahora, analiza una situación en donde esté presente un prisma triangular.
Fátima es una estudiante de primaria. Recientemente, le dejaron realizar un caleidoscopio, este es un instrumento que produce una serie de imágenes con simetría hexagonal.
Para su construcción necesitó 3 espejos en forma rectangular y los debe colocar dos a dos en un ángulo determinado; formando, así, un prisma de base triangular.
El caleidoscopio se elabora de esta manera para que cada uno de los pares de espejos produzcan seis imágenes simétricas de los objetos que se colocan dentro de él. Fátima se ha preguntado cuál será el volumen del caleidoscopio.
Pon atención al siguiente procedimiento y toma nota de la información más relevante. Se te sugiere repliques en tu cuaderno, o en hojas reutilizables, el esquema del caleidoscopio que se te presenta a continuación.
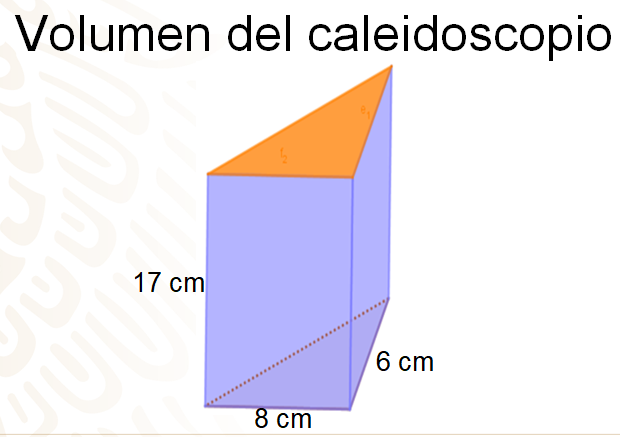
Como puedes ver en la imagen, el caleidoscopio tiene las siguientes dimensiones: 17 centímetros de largo, 8 centímetros de ancho y de altura 6 centímetros. Su contorno es de color lila, con forma de un rectángulo.
Con esta información ya puedes dar respuesta a la pregunta planteada: ¿Cuál será el volumen del caleidoscopio?
Se te sugiere poner atención al siguiente procedimiento.
¿Qué fórmula deberás utilizar para calcular el volumen de un prisma recto?
Debes utilizar la siguiente fórmula: Volumen = Área de la base por altura. Con esta información podrás calcular el volumen del caleidoscopio. Primero, obtendrás el área de la base; es decir, encontrarás el área del triángulo.
La fórmula para calcular el área del triángulo es: base por altura entre dos, como lo viste anteriormente. Ten mucho cuidado de no confundir la altura de la base con la altura del prisma.
Multiplicarás 8 centímetros por 6 centímetros. El producto es 48 centímetros cuadrados, entre dos, que es igual a 24 centímetros cuadrados. Ahora, encuentra el volumen multiplicando el área de la base por la altura del caleidoscopio, que es de 17 centímetros; de este modo, tienes que 24 centímetros cuadrados por 17 centímetros, da como resultado 408 centímetros cúbicos.

Hasta el momento, has analizado dos situaciones en donde viste la relación que existe entre la capacidad y el volumen en un prisma rectangular, también conocido como paralelepípedo; y el cálculo del volumen en un prisma triangular.
Ahora, analiza el siguiente caso.
Jesús trabaja en una empresa en donde elaboran veladoras que tienen una medida de 15 cm de ancho, 15 cm de largo y 15 cm de profundidad. Se te sugiere escribir las siguientes preguntas para reflexionar: ¿Qué volumen tendrá cada veladora?, ¿qué forma tienen estas veladoras?
Primero encuentra qué forma tienen las veladoras. Las veladoras tienen forma de un cubo, debido a que sus tres medidas son iguales.
Para encontrar el volumen de cada veladora, puedes utilizar la siguiente fórmula: Volumen = lado por lado por lado o lado elevado a la tercera potencia.
Calcula el volumen del cubo con la siguiente fórmula:
Volumen = lado, elevado a la tercera potencia.
Con esta información podrás calcular el volumen de cada veladora, por lo que multiplicarás 15 centímetros, por 15 centímetros, por 15 centímetros, cuyo producto es 3 375 centímetros cúbicos.

Como te pudiste dar cuenta, el cálculo del área y el cálculo del volumen se encuentran presentes en varias situaciones cotidianas y es de fundamental importancia conocer cómo obtenerlas.
Calcular el área es importante en varios trabajos. Un ejemplo distinto a los analizados en esta sesión es la construcción; ya que, para aplanar una pared, colocar loseta en el piso de alguna casa o escuela o en alguna otra situación similar.
La unidad de medida que se utiliza comúnmente es la unidad cuadrática, para así obtener una estimación de cuánto material y dinero se ocupará para realizar el trabajo. Los topógrafos, que son especialistas en el ámbito de la cartografía, también utilizan el cálculo del área; por ejemplo, para obtener el área de una parcela en un terreno en el que se tenga que construir una casa, una granja, un centro comercial, un parque, etcétera.
Además de las situaciones que analizaste en la sesión con respecto al cálculo del volumen y la relación que existe entre éste y la capacidad, es fundamental, hoy en día conocerla; ya que en varias empresas donde envasan leche, jugos, refrescos o alguna otra bebida, se emplea este cálculo para conocer exactamente las dimensiones del envase de cartón o de vidrio que deben elaborar y si en él caben los litros o mililitros de la bebida que se desea envasar.
Como puedes ver, las matemáticas son utilizadas en varias situaciones cotidianas, en donde menos no lo esperas; es por ello, la importancia de su estudio.
El reto de hoy:
Se te invita a que revises en tu libro de texto los temas que estudiaste en esta sesión y realiza las actividades que ahí se te sugieren.
Asimismo, concluye los ejercicios que se realizaron en el desarrollo de la sesión, en caso de que te hayan quedado pendientes.
¡Buen trabajo!
Gracias por tu esfuerzo.
* Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas