Antecedentes y fundamentos II
Antecedentes y fundamentos II
Aprendizaje esperado: explica la diferencia entre eventos complementarios, mutuamente excluyentes e independientes.
Énfasis: explicar la diferencia entre eventos.
¿Qué vamos a aprender?
Aprenderás la diferencia entre eventos complementarios, mutuamente excluyentes e independientes y la diferencia entre eventos.
Los materiales que vas a utilizar son: cuaderno, lápiz, goma, una moneda de cualquier valor, 2 dados y 8 canicas.
Es muy importante que tomes nota de cada una de las dudas que surjan durante el desarrollo de la sesión para que puedas compartirlas con tus compañeras, compañeros y profesores.
En caso de que no tengas los materiales, como el dado o las canicas, existen algunas opciones alternas.
Por ejemplo, en una hoja de papel traza 8 círculos y los coloreas, será una simulación de las canicas.
¿Qué hacemos?
En el caso de no contar con el dado, puedes construir uno con materiales que tengas en casa, observa el siguiente video.
- Elaboración de un dado
Es importante que utilices material rígido en la construcción del dado, para que en el lanzamiento éste no se deforme.
Como dato curioso, sabías que el dado cúbico más antiguo que se conoce data de 3000 a. C., es de cerámica y fue encontrado en Irán.
Los números en las caras varían según los lugares y las épocas, pero la ordenación más común es la parecida a la actual.
Por cierto, en la sesión anterior aprendiste algunos conceptos de azar, como espacio muestral, evento seguro, evento imposible, y resolviste preguntas como:
¿Cuál es el espacio muestral de lanzar una moneda dos veces?
¿Cuál es el espacio muestral del lanzamiento de una moneda y un dado?
La idea es que puedas verificar tus resultados.
Para conocer el espacio muestral de lanzar una moneda dos veces es necesario saber cuáles son todos los posibles resultados del experimento.
Para resolver las situaciones, puedes utilizar un arreglo rectangular, comienza con la primera pregunta: ¿Cuál es el espacio muestral de lanzar 2 monedas?
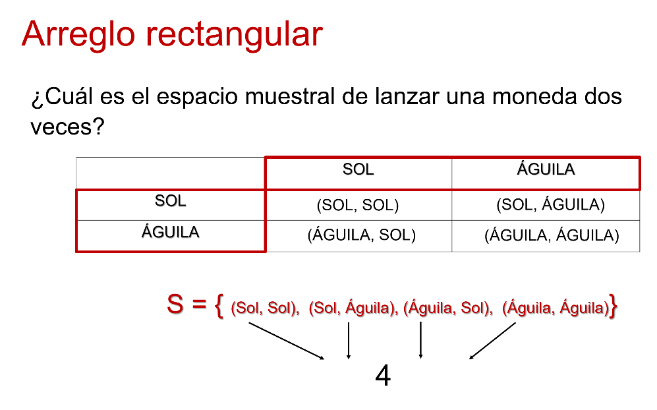
Un arreglo rectangular que es una tabla donde en la fila pones todos los posibles resultados de una de las monedas y en la columna todos los posibles resultados de la otra moneda. Entonces, combinando ambos resultados obtienes que el espacio muestral del lanzamiento de una moneda dos veces es:
- Sol y sol
- Sol y águila
- Águila y águila
- Águila y sol
Es decir, tienes 4 resultados totales del lanzamiento de 2 monedas.
Ahora, ¿cuál es el espacio muestral del lanzamiento de una moneda y un dado?
Utiliza nuevamente un arreglo rectangular para resolverlo.
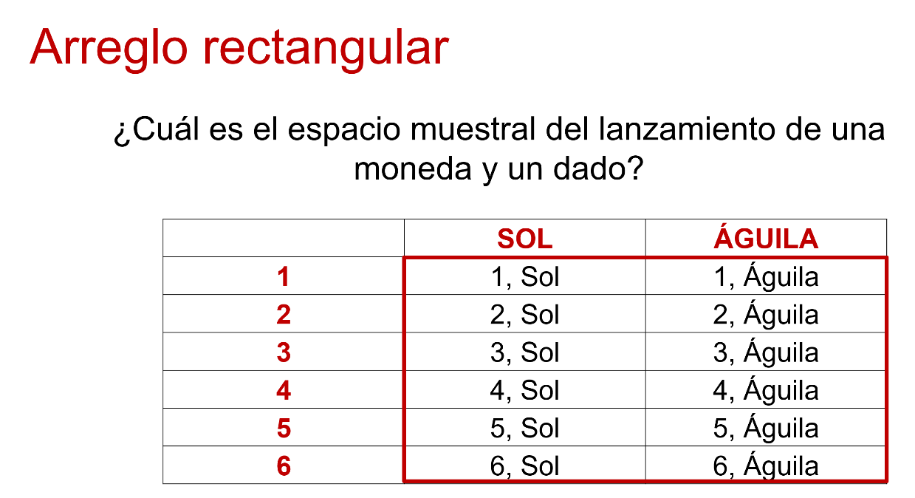
En la columna escribes todos los posibles resultados de uno de los dados y en la fila escribes todos los posibles resultados del otro dado; entonces, combinando ambos resultados obtienes el espacio muestral del lanzamiento de ambas monedas. Si observas todos los posibles resultados del experimento, son doce.
Esta es la respuesta del reto que se dejó en la sesión anterior. Pero también aprendiste el concepto de evento.
Resuelve la siguiente situación:
Maximiliano les propuso un juego a 6 de sus amigos, éste se llama “La carrera de caballos”.
Consiste en elegir uno de 12 caballos que competirán, Maximiliano eligió el número 7 y el resto de sus amigos, como se muestra en la tabla.
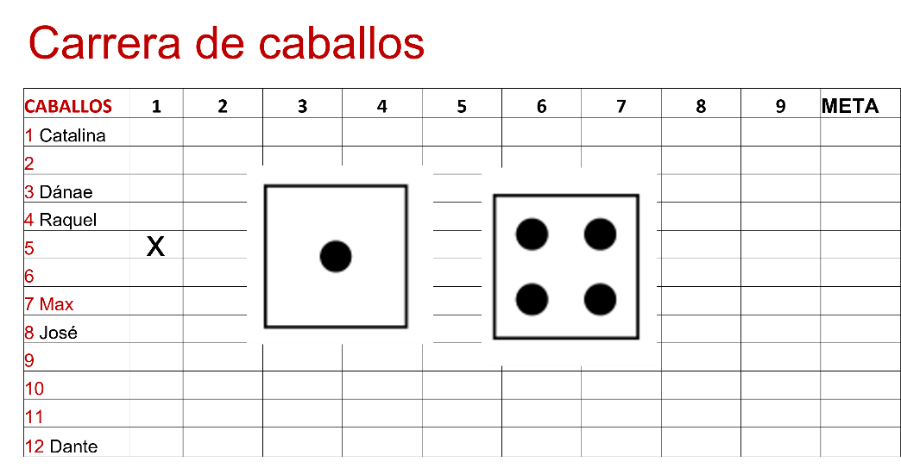
Una vez que sus amigos eligieron el caballo, él les dijo que para que avanzaran deberían lanzar 2 dados de manera simultánea y que la suma de las caras de ambos dados sería el caballo que avanzaría.
Por ejemplo, si saliera 1 y 4, la suma es 5, por lo tanto, avanza el caballo 5, aun cuando no tenga dueño, el caballo avanza y se va registrando en el tablero. Los resultados del juego de Maximiliano y sus amigos fueron los siguientes.
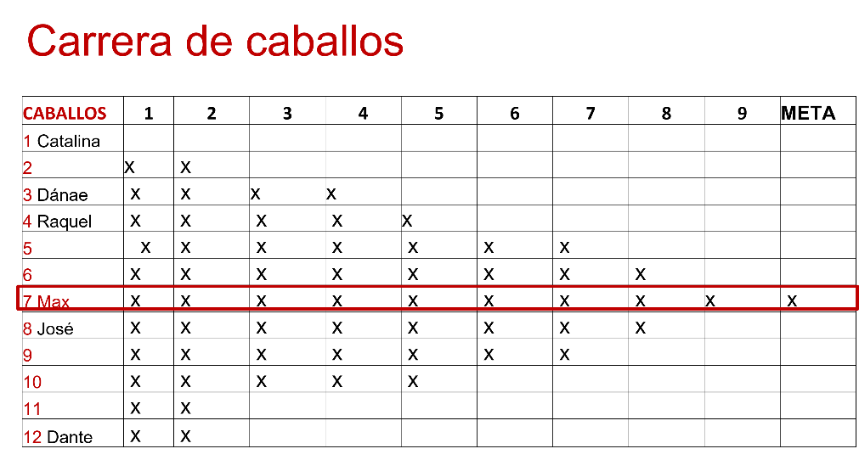
El ganador fue Maximiliano. Si observas, Catalina jamás avanzó. Esto es porque la suma mínima de las caras de ambos dados es 2, es decir, en un dado cae 1 y en otro 1 la suma es 2, por eso el caballo 1 jamás podía avanzar, es decir, es un evento imposible.
Observa los resultados, el caballo que eligió José también estaba acercándose a la meta. Busca los casos favorables para que avance el caballo 4, que fue el que eligió Raquel.
Para observar el avance del caballo 4, se debe tener en cuenta el espacio muestral. Como puedes observar, todos los posibles resultados del experimento son 36; por lo tanto, tienes que casos favorables de que la suma de las caras de los dados sea 4, son tres casos favorables de 36 casos totales.
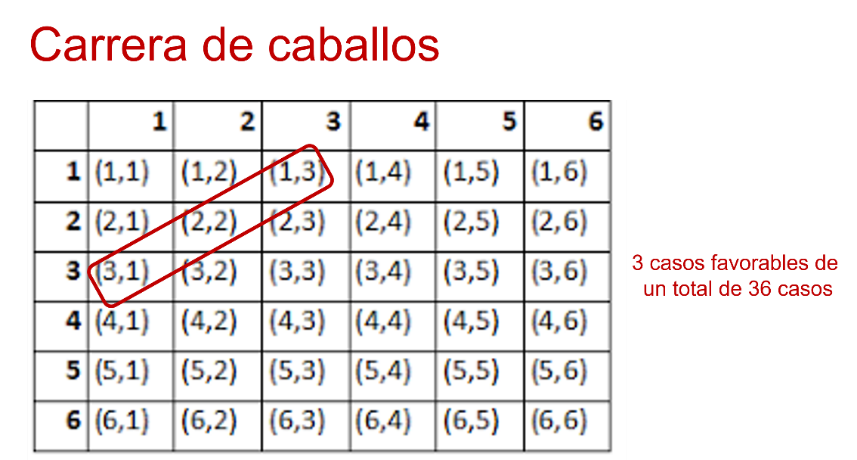
Ahora observa los casos favorables de que avance el caballo 7.
Si los cuentas son seis casos favorables de que salga el caballo siete y el total de casos son 36.
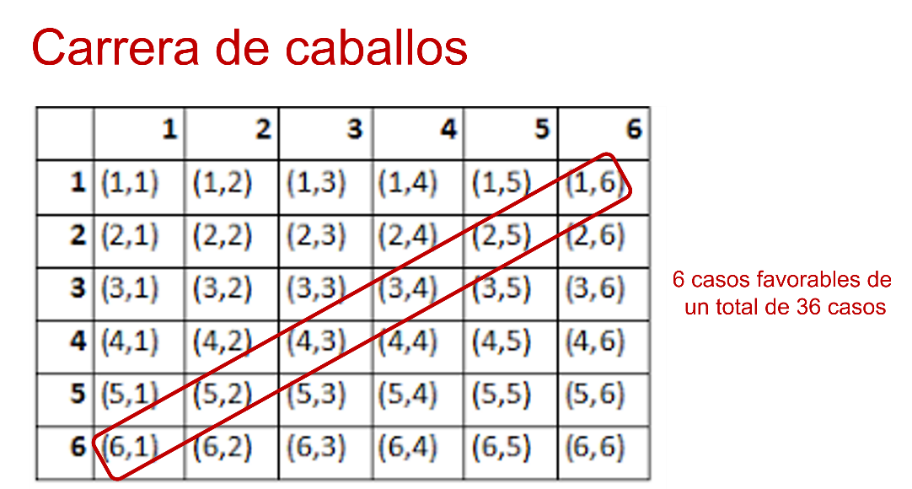
Ahora, cuenta cuántos casos favorables existen de que avance el caballo 12.
Si cuentas, tienes que sólo hay un caso favorable de 36 casos totales.

Recuerda que, en el juego quien ganó fue el caballo 7, que eligió Maximiliano.
Esto es porque tiene más casos favorables para avanzar a diferencia del resto de los otros caballos. Si se repite el juego varias veces podrás observar que regularmente ganan los caballos que tienen mayor número de casos favorables.
En este tipo de juegos, a diferencia de un volado, ningún jugador tendrá las mismas posibilidades de ganar.
Resuelve la siguiente situación.
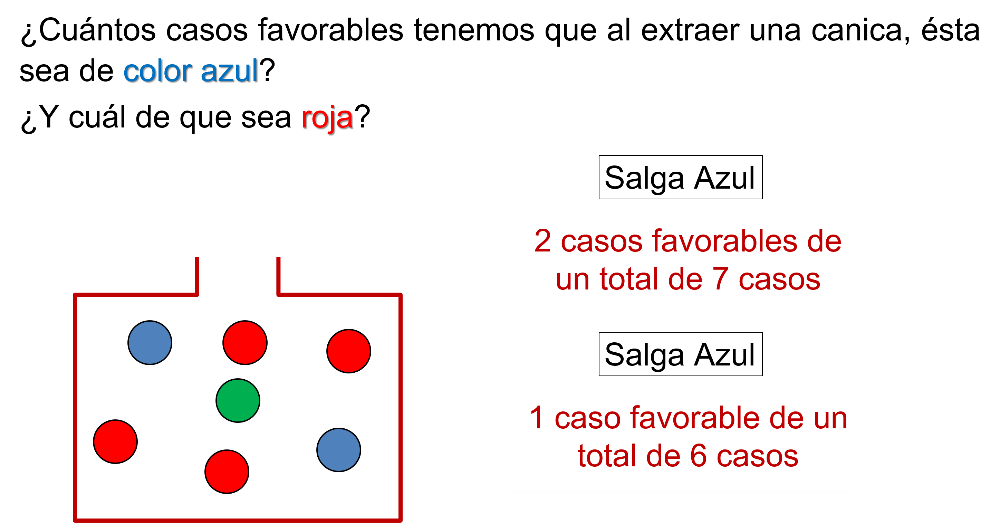
En una urna hay 4 canicas rojas, 2 azules y 1 verde. ¿Cuántos casos favorables existen que, al extraer una canica, ésta sea de color azul? ¿Y cuál de que sea verde?
Si cuentas las canicas dentro de la urna, los casos favorables, es decir, que salga azul, es 2 y el total de casos posibles son 7.
Cuenta ahora ¿cuántos casos favorables hay de que salga roja? Los casos favorables, es decir, que salga verde son 4 y el total de casos posibles son 7.
Si se extrae una canica azul puedes ver que hay 2 casos favorables de un total de 7 casos; si al extraerse esa canica y no se regresa a la urna, puedes darte cuenta de que para la siguiente extracción el espacio muestral cambia porque ahora se tendrán 6 casos en total.
Entonces, ¿cuántos casos favorables hay de que nuevamente salga azul?
Un caso favorable de un total de 6 casos.
Por lo tanto, si en un experimento como el de las canicas se hace una extracción sin remplazo; es decir, no se regresa a la urna, el espacio muestral cambia a diferencia de si existe un remplazo (regresarlo a la urna).
Para que quede aún más claro, resuelve la siguiente situación.
Una caja contiene 8 canicas: 6 rojas y 2 azules. Se realiza una extracción reponiendo la canica extraída a la caja antes de la siguiente extracción.

Si observas, en ambos eventos el espacio muestral es el mismo, 8 casos totales.
¿Sucederá lo mismo si realizo extracciones sin regresarlas a la caja? Observa:
Tienes la misma caja con 8 canicas: 6 rojas y 2 azules. Se realiza una extracción sin reponer la canica de la caja antes de la siguiente extracción.
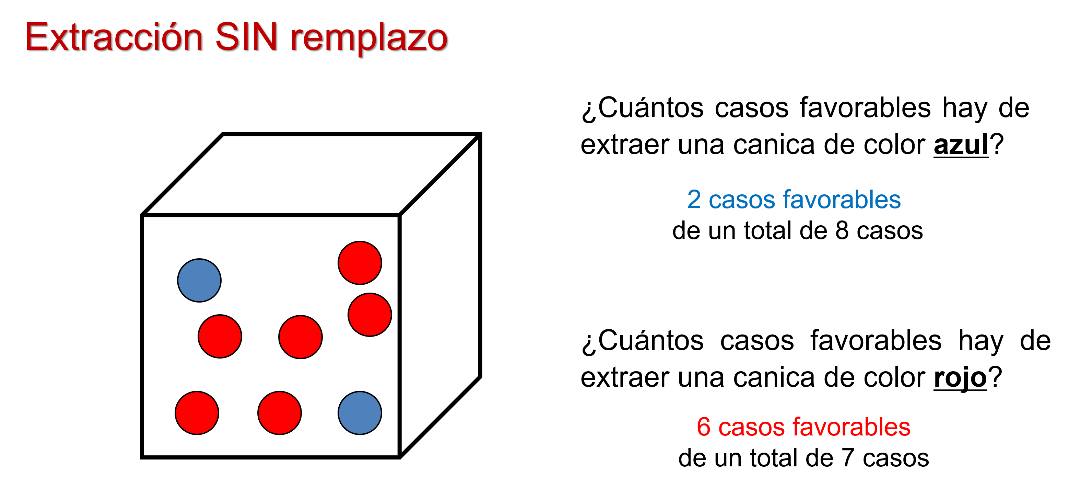
¿Qué significa la frase: sin reponer la canica de la caja antes de la siguiente extracción? Significa que al extraer una canica una vez que observes de qué color es, no la regreses a la caja y cuando realices la segunda extracción esa canica ya no estará en la caja.
A eso se le conoce como extracción SIN reemplazamiento.
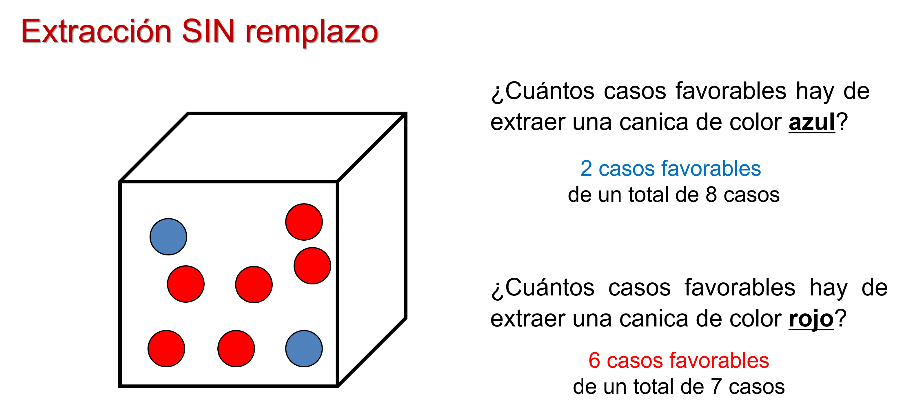
Ahora retira la canica roja.
Si observas el espacio muestral, va cambiando conforme extraes las canicas.
Resuelve el siguiente problema:
Se lanza una moneda y un dado, ¿cuántos casos favorables existen de que salga sol y 3?
Para saberlo debes contar cuántas posibilidades existen de que salga sol y 3, por eso es necesario conocer el espacio muestral, es decir, todos los posibles resultados del experimento. Observa que tienes 12 casos totales. Y uno es la cantidad de casos favorables de que salga sol y 3.
Del mismo experimento, lanzar una moneda y dado

Cuenta ¿cuántos casos favorables existen de que salga águila y par? En total son 3 casos favorables de 12 casos en total.

Ahora cuenta los casos favorables de que salga sol y un número mayor que 3.

Observa que tienes 3 casos favorables de un total de 12 casos. Observa una forma de conteo: los diagramas de árbol.
Los diagramas de árbol se usan para encontrar todos los resultados posibles de un experimento, que se lleva a cabo en un número finito de maneras.
Construye el diagrama de árbol para encontrar las formas de combinar a, b y c.
Partimos de un nodo, y se presentan las primeras opciones de combinación, a, b y c.
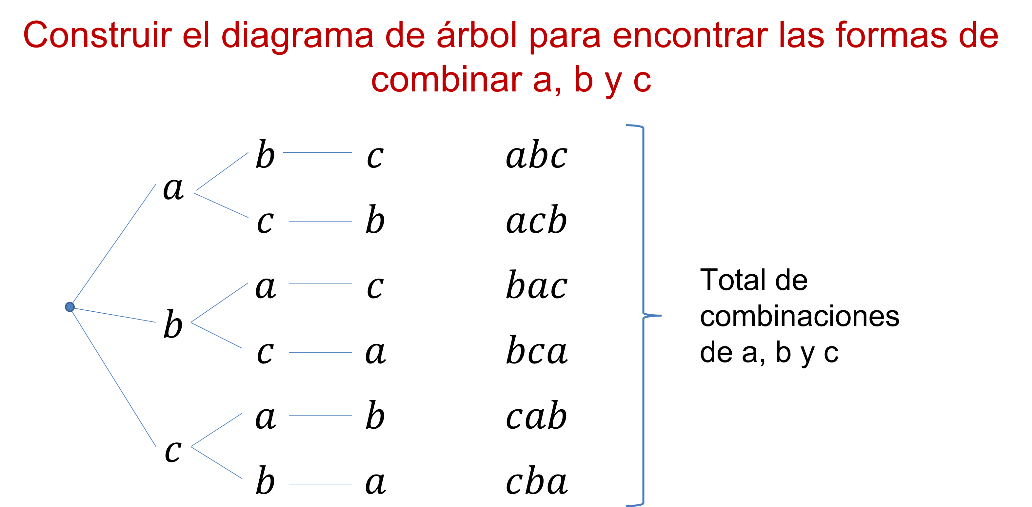
Luego, en cada caso se presentan las opciones a que dan lugar. Después, se colocan las opciones que siguen a las segundas quedando al final todas las combinaciones de a, b y c.
Usa el diagrama de árbol para otro problema.
Ana y María juegan tenis. Hicieron una pequeña competencia entre ellas: la primera que gane dos juegos seguidos o que complete tres, gana su competencia. El diagrama siguiente muestra los posibles resultados de la competencia. Puedes observar que hay 10 rutas que cumplen las condiciones para ganar.
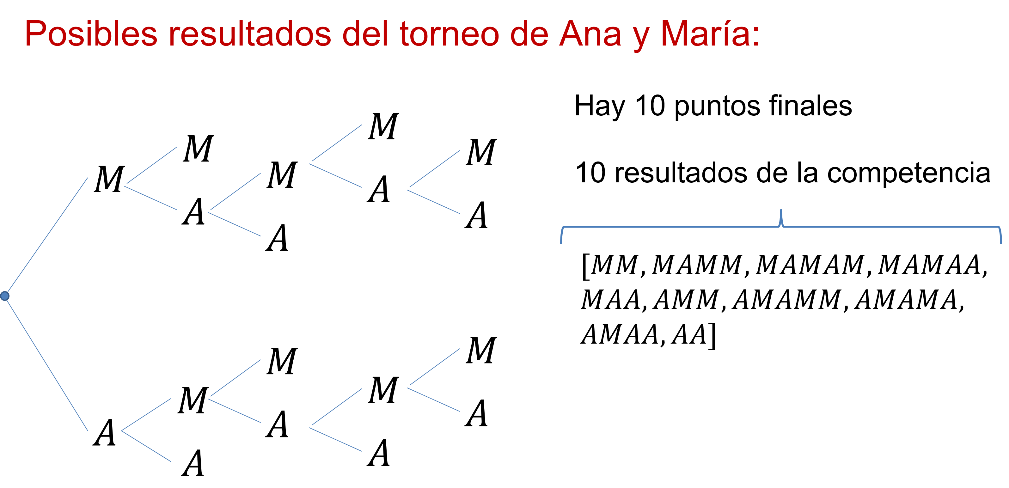
Ahora, usa esta manera de contar en los siguientes problemas.
Jesús y Laura son hermanos y entre los dos han decidido contribuir con las labores de su casa. Jesús propone lanzar una moneda dos veces, y de esa manera decidir quién hará cada tarea. Ellos deciden utilizar un diagrama de árbol para conocer todos los posibles resultados del experimento.
Recuerda, un diagrama de árbol es la representación gráfica para identificar los posibles resultados en un evento aleatorio. También es una herramienta útil para determinar el espacio muestral de un experimento con eventos múltiples. Así es como queda el diagrama de árbol de lanzar una moneda y un dado:
Para hacer el diagrama de árbol comienza con las ramas de primera generación, sabemos que al lanzar una moneda puede caer sol o águila.
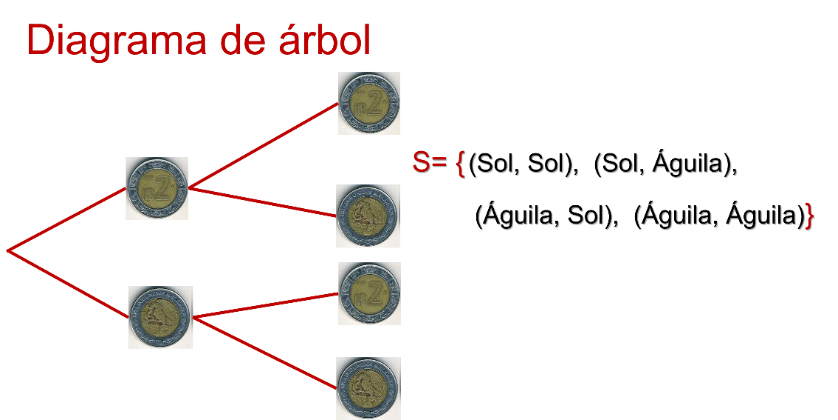
Ahora, pasa al segundo lanzamiento de la moneda.
Como puedes darte cuenta, son 4 los posibles resultados de lanzar una moneda dos veces.
Si de los hermanos, Laura eligió disparejo cuenta cuántos casos favorables tiene Laura en su elección. Se entiende por disparejo en un volado de 2 lanzamientos de una moneda, cuando cae en el primer lanzamiento sol y águila y en otro lanzamiento águila y sol
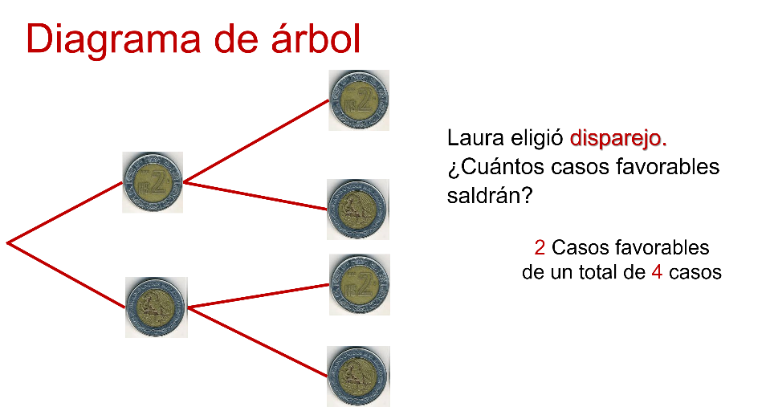
Apoyándonos del diagrama de árbol te puedes dar cuenta de que la elección de Laura es: 2 casos favorables de un total de 4 casos.
Ahora observa un experimento donde intervenga un dado, una moneda, una canica verde y una canica azul. ¿Es posible usar un arreglo rectangular? No, porque con el arreglo rectangular sólo se podrían combinar 2 elementos.
Para obtener el espacio muestral del experimento (lanzar un dado, una moneda y una canica) vas a utilizar un diagrama de árbol.
Si observas, el diagrama de árbol quedó muy grande, pero ayudará a identificar más fácil los casos favorables.
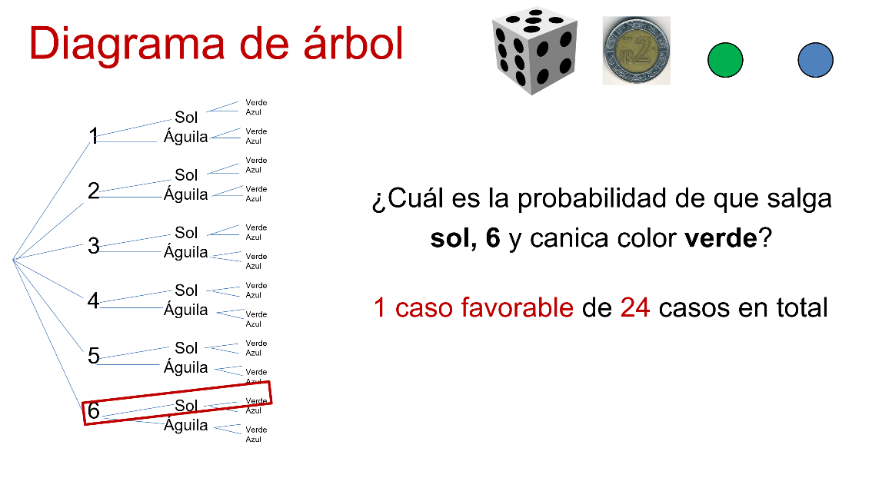
Del mismo experimento cuenta cuántas posibilidades existen de que salga águila, número par y canica color azul.
Realiza el conteo o marca en el diagrama de árbol las opciones sol, 6 y canica verde.

Observa otra situación, ésta proviene de un libro de texto. Si lanzas dos dados y sumas los puntos que salen cara arriba. ¿Qué suma sale más veces? ¿Por qué? Cuenta ayudándote de los diagramas de árbol.
Analiza los diagramas de árbol. ¿Qué suma sale más veces? Observa bien el diagrama.

La suma de 7, porque se presenta más veces.
1 + 6, 2 + 5, 3 + 4, 4 + 3, 5 + 2, 6 + 1 son siete casos favorables.

¿Qué suma aparece menos veces? La suma de 2 porque sólo hay una combinación 1 + 1.
Recuerda que un espacio muestral es el conjunto de todos los resultados posibles de un experimento y lo identificas con la letra S; en el lanzamiento de una moneda, todos los posibles resultados son 2, sol y águila.

Un evento es un subconjunto de un espacio muestral o, en otras palabras, es un suceso aleatorio dentro del espacio muestral.

Un evento imposible es aquel que nunca llega a ocurrir, y un evento seguro es aquel que siempre va a ocurrir y es llamado también evento determinístico. Diagrama de árbol: es la representación gráfica para identificar los posibles resultados en un evento aleatorio.
Darás un repaso de lo aprendido en esta sesión, cuyo propósito fue conocer algunos conceptos relacionados con el azar, como el espacio muestral y contar los casos favorables y totales de eventos, así como identificar qué es y cómo utilizar un diagrama de árbol.
Te sugerimos que los escribas en tu cuaderno con tus propias palabras, será de utilidad para las próximas sesiones.
Ejemplifica cómo el evento imposible es aquel que nunca llega a ocurrir, cómo en la carrera de caballos cuando una amiga de Maximiliano eligió el caballo 1, el cual jamás avanzó porque al lanzar dos dados, la suma mínima era 2.
También aprendiste cómo contar los eventos favorables en un espacio muestral y lo que es un arreglo rectangular y cómo éste te puede servir para encontrar el espacio muestral, es decir, todos los posibles resultados de un experimento.
El reto de hoy:
El primer reto es:
¿Recuerdas el juego de carrera de caballos? Pues ahora es tu turno de jugarlo con algunos de tus familiares.
Considera que podrás participar hasta un máximo de 12 jugadores, ya que son 12 caballos dentro de la carrera.
Toma en cuenta que debes utilizar 2 dados o bien el lanzamiento de un dado dos veces, ya que el caballo que avanzará será el que indique la suma del número de caras que salió.
Traza en tu cuaderno un arreglo rectangular para que puedas apoyarte de el al realizar el juego con tu familia. Recuerda darles las indicaciones correctas.
El segundo reto será buscar en tu libro de texto el tema abordado. Recuerda apoyarte en el índice para que sea más fácil.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más: