Análisis de una gráfica al modificar una de las variables
Análisis de una gráfica al modificar una de las variables
Aprendizaje esperado: analiza y compara situaciones de variación lineal a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación.
Énfasis: analizar las gráficas de variación lineal de la forma y = ax + b cuando se modifica a o b y la otra es constante.
¿Qué vamos a aprender?
En esta sesión trabajarás con el Aprendizaje esperado: “Analiza y compara situaciones de variación lineal a partir de sus representaciones tabular, gráfica y algebraica. Interpretarás y resolverás problemas que se modelan con este tipo de variación”.
Se te recomienda que para el desempeño de tus actividades tengas a la mano tu cuaderno u hojas reutilizables, lápiz, goma, regla, tu libro de texto de la asignatura. En caso de tener una discapacidad visual, prepara hojas leyer, un punzón y una regleta.
¿Qué hacemos?
Hace un par de años, una compañera tuya Andrea, conoció a la vocalista de un grupo independiente de música pop, ella le comentó a Andrea que tenían ya varios años juntos y que, al ser un grupo de música independiente, eran ellos mismos quienes creaban sus melodías y las letras de sus canciones. Con el paso de los años, eran más las personas a las que les atraía su música, así que decidieron publicar sus canciones en una plataforma digital de contenido auditivo. Cada semana, podían ver el total de reproducciones de sus canciones y notaron que, una canción en particular tuvo mucho éxito, ya que cada semana aumentaba el número de reproducciones. Para ilustrar este ejemplo, se muestra la siguiente gráfica.

Como puedes observar en la gráfica, el aumento en el número de reproducciones de la canción, semana a semana, fue constante; en la primera semana, el número reproducciones fue de 300; durante la semana 3, se registraron 600 reproducciones; y en la quinta semana, la canción tuvo 900 reproducciones.
¿Cómo aumentó el número de reproducciones semana a semana? Es decir, ¿cuál es la razón de cambio de la situación?
Para establecer la razón de cambio de la situación presentada, analiza las coordenadas por donde pasa la recta y, así, poder contestar la pregunta. Primero, tienes que recordar que la razón de cambio es la medida en la cual se modifica una variable, con relación a la otra.
Observa nuevamente la gráfica.
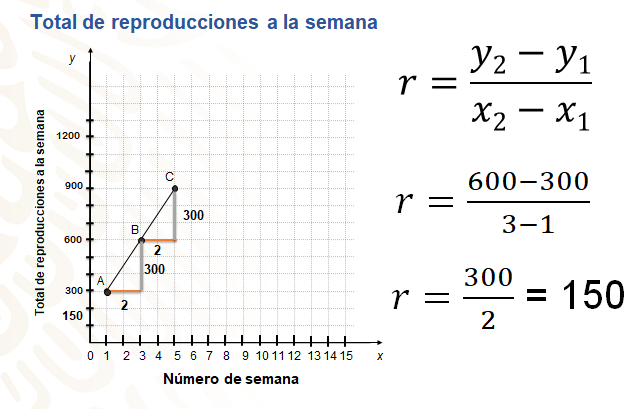
Para establecer la razón de cambio, necesitas los valores de “x” y de “y” de dos puntos coordenados, calculas la diferencia entre las dos “y” y las dos “x” de esos dos puntos y divides las diferencias de las “y” entre la diferencia de las “x”. Por ejemplo, se seleccionan las coordenadas de dos puntos pertenecientes a una gráfica (1,300) y (3,600), entonces calculas la razón de cambio, 600 menos 300, entre 3, menos 1.
Lo anterior, lo puedes observar en la gráfica: del punto A al B, hay una diferencia en “ye” de 300 y en “x” de 2; del punto B al C, hay una diferencia de 300 en “ye” y de 2 en “x”. Por lo tanto, si se divide 300 entre 2, se obtiene que la razón de cambio es igual 150.
De lo anterior, se puede deducir que el número de reproducciones, cada semana tuvo 150 más que la semana anterior, es decir, semana a semana, aumento de 150 en 150, de manera constante.
Ya recordaste el significado de la razón de cambio y como obtenerla, esto te ayudará a analizar y resolver las siguientes situaciones.
La vocalista del grupo de rock le contó a Andrea que, por unirse a la plataforma digital, se les otorga una comisión semanal de 200 pesos; y que, por cada una de las reproducciones de una canción, el grupo recibe 0.50 pesos; es decir, 50 centavos.
¿Cuál es la expresión algebraica con la que se puede calcular la ganancia semanal que obtiene el grupo musical?
Para calcular la ganancia semanal, representada por la literal “ye”, debes multiplicar el total de reproducciones, que estará representada con “x”, por los cincuenta centavos y, posteriormente, sumarle la comisión que se entrega a la semana, que es de 200 pesos. Es decir, ye es igual a 0.50x más 200.

Ahora, calcula la ganancia monetaria que obtuvo el grupo en la semana 1, considerando que, en esa semana, la canción tuvo 300 reproducciones.
Sabiendo que la comisión semanal es de 200 pesos y que, por cada reproducción cobran 0.50 pesos, para calcular la ganancia semanal (ye), debes multiplicar 0.50 pesos por 300 y, posteriormente, sumarle 200. Así, se tiene que el resultado de la multiplicación es 150, sumas la comisión semanal de 200 pesos y obtienes que la ganancia del grupo, durante la primera semana, que fue de 350 pesos.

En la tercera semana, el número de reproducciones de la canción fue de 600. Para calcular la ganancia total que recibió el grupo por esa canción que tuvo tanto éxito, puedes hacerlo de la misma manera.
A partir de la expresión y = 0.50x + 200, debes multiplicar los 50 centavos que se reciben por cada reproducción, por las 600 reproducciones de esa semana y, posteriormente, le sumas la comisión semanal que son 200 pesos; así tienes que el producto es de 300 más 200 de la comisión te da como resultado 500 pesos de ganancia, en esa semana.

Ahora, ¿puedes decir cuál es la ganancia total por las 900 reproducciones que se registraron en la quinta semana?
De nuevo, multiplicas los 50 centavos, esta vez por 900, lo que da como resultado 450; luego sumas los 200 pesos de la comisión semanal y obtienes 650 pesos de ganancia en esa semana, en la que el total de reproducciones fue de 900.

Ahora, revisa la gráfica que representa la ganancia semanal, que obtuvo el grupo en estas tres semanas. ¿Cómo piensas que será?
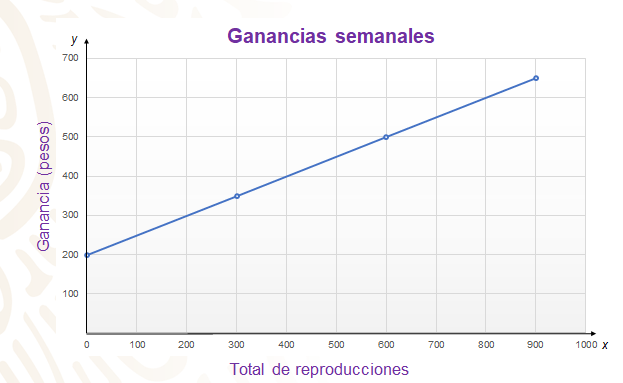
Como puedes observar, la gráfica es una recta cuyo primer punto se ubica en la coordenada (0, 200); debido a que, cuando el grupo se integra a la plataforma, recibe una comisión de 200 pesos. El siguiente punto corresponde a las 300 reproducciones con una ganancia de 350 pesos; el siguiente a las 600 reproducciones que les dan 500 pesos de ganancia y por último se tienen las 900 reproducciones con los 650 pesos. Al analizar la gráfica puedes ver que la situación representa una situación de variación lineal de la forma y = ax + b.
El grupo musical se dio a la tarea de investigar las comisiones y pagos por reproducción que otorgaba otra plataforma digital.
La segunda plataforma ofrecía 70 centavos por reproducción y la misma comisión semanal, de $200. Calcula la ganancia que hubieran obtenido por las 300, 600 y 900 reproducciones en esta plataforma.

- ¿Qué expresión algebraica representa esta situación?
- ¿Qué características tendrá la gráfica, comparada con la anterior?
La expresión algebraica para este caso es, y = 0.70x + 200.
En primer lugar, tienes que calcular la ganancia en esta plataforma por 300 reproducciones; para ello, multiplicas 300 por 0.70, más 200.
El resultado es 410; es decir, la ganancia por 300 reproducciones en esta plataforma es de 410 pesos.
Para las 600 reproducciones, multiplicas este número por 0.70 y al producto le sumas 200. El resultado es 620 pesos.
Por último, 900 por 0.70 es igual a 630 pesos, más los 200 pesos de la comisión, obtienes como resultado 830 pesos de ganancia, en esa semana.

Ahora, observa la gráfica que representa las ganancias, que se obtienen en esta nueva plataforma.
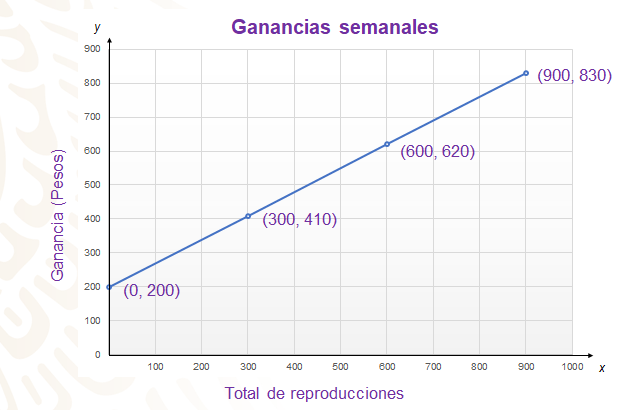
Como puedes observar, en la gráfica se muestran los puntos que corresponden a las ganancias, que se obtendrían según el número de reproducciones. El primer punto, corresponde a la comisión que se entrega al incorporarse a la plataforma; el siguiente a los 410 pesos por 300 reproducciones; el subsecuente punto, 620 pesos que se entregan por las 600 reproducciones que se registraron; y, el último, la ganancia de 830 pesos por 900 reproducciones.
Enseguida, analizarás la gráfica de una tercera plataforma digital y se determinará la razón de cambio y la expresión algebraica que representa la situación.

Observa la gráfica. Al igual que las anteriores, inicia en la coordenada (0, 200), lo que significa que el grupo recibiría 200 pesos al momento en el que se integra a la plataforma; enseguida puedes ver el punto de las 300 reproducciones, por las que se obtienen 290 pesos de ganancia; después puedes observar que, por 600 reproducciones, pagan 380 pesos y, por último, por 900 reproducciones la ganancia es de 470 pesos.
- ¿Cuál es la razón de cambio?
- ¿Qué expresión algebraica permite calcular la ganancia para cualquier número de reproducciones?
Para establecer la razón de cambio, ubicas dos coordenadas, calculas la diferencia entre los valores de ye y los respectivos de x y divides los resultados.
En este caso, 380 menos 290, entre 600 menos 300, es igual a 90 entre 300, igual a 0.3, que corresponde a la razón de cambio, que, en este caso, representa el pago por cada reproducción. De lo anterior, se puede establecer la expresión algebraica de esta tercera plataforma que es: y = 0.30x + 200.
Ya has visto la gráfica que refleja la información sobre las ganancias que obtendría el grupo musical en cada una de las 3 plataformas de audio digital. ¿Qué pasaría si analizas las tres rectas en un mismo plano cartesiano? ¿Qué recta tendría mayor inclinación? ¿Qué determina la inclinación de las rectas?
Observa.

Analiza las rectas y piensa, ¿en qué se parecen? ¿En qué son diferentes? ¿Cuál representa cada situación?
Ahora, analiza las siguientes preguntas: ¿Por qué inician en el mismo punto? ¿Por qué la inclinación de la recta es diferente?
Hay que contestar las preguntas. Las tres son líneas rectas, ya que representan relaciones de variación lineal, de la forma y = ax + b.
Por otro lado, las tres rectas inician en el mismo punto, que en la expresión algebraica corresponde al valor de b; es decir, corresponde a la coordenada (0, b), ya que en las tres plataformas de audio digital entregan 200 pesos al integrarse a ella. Pero la inclinación es diferente ya que, aunque en las tres se entrega la misma comisión, el pago que otorgan por cada reproducción que se registra, no es la misma. Tomando en cuenta esto, observa de nuevo las gráficas.
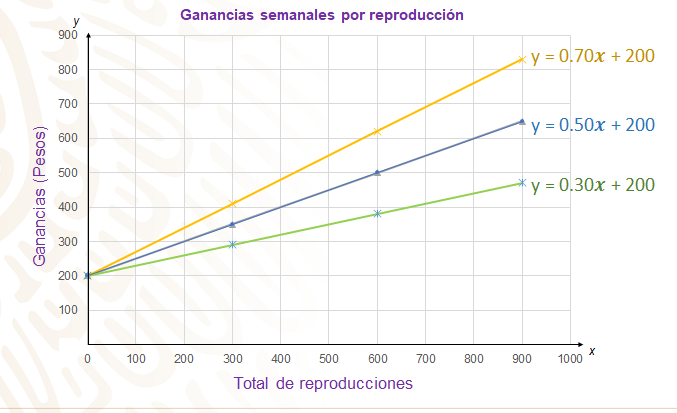
¿Puedes decir cuál es la línea recta que pertenece a la plataforma que analizaste en primer lugar?, ¿cuál es la que analizaste en segundo? y ¿cuál es la recta que representa la información de la plataforma de audio digital número 3?
Observa atentamente y contesta las preguntas.
Efectivamente, la recta que representa a la plataforma 1 es la que tiene un color azul, y su expresión algebraica es y = 0.5x+ 200; la que representa a la segunda plataforma tiene el color amarillo, la expresión algebraica es y=0.70x+200; y la recta de color verde, es la que representa las ganancias que se otorgan en la plataforma que analizaste en tercer lugar, la expresión algebraica es y=0.30x+200.
Al observar cada una de las rectas y la expresión algebraica que les corresponde, puedes determinar qué término de la expresión determina que la inclinación de la recta cambie; así que, en la siguiente generalización, identifica qué parte es la que determina lo anterior.
En la expresión general y = ax + b, la literal “a” corresponde a la razón de cambio y te indica la pendiente que tendrá la recta. Cuanto mayor sea “a” o la razón de cambio, la pendiente estará más inclinada hacia el eje de las ordenadas o bien, el eje “ye”. Tal y como lo acabas de observar, con la línea recta que representa a la plataforma digital que otorga más dinero por cada una de las reproducciones, observa de nuevo.
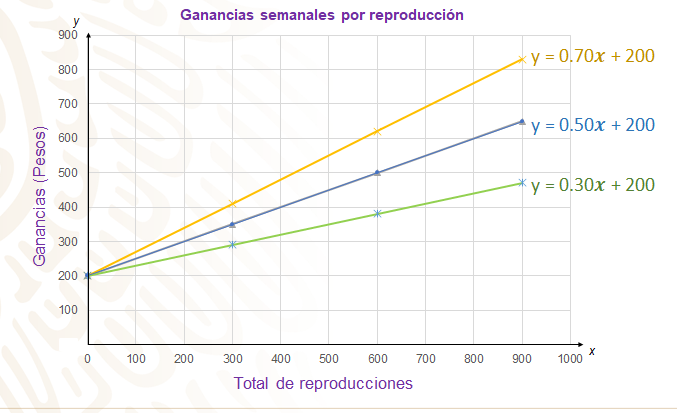
Las tres rectas tienen la misma ordenada al origen; es decir, “b” tiene el mismo valor, pero la pendiente de las rectas es diferente y depende de la razón de cambio. En este caso, en la recta amarilla, la razón de cambio es mayor, ya que otorgan 70 centavos por reproducción; entonces tiene mayor inclinación; es decir, mayor pendiente.
Ya analizaste las gráficas sobre las ganancias que otorgan tres plataformas digitales en las que la comisión semanal no cambia.
Reflexiona. Si la comisión por ingresar a la plataforma aumenta o disminuye y el pago por reproducción se mantiene constante, ¿qué sucedería?, ¿cómo se reflejaría esto en la gráfica correspondiente?
Analiza tres casos para dar respuesta a las preguntas anteriores.
Las tres plataformas pagan lo mismo por cada reproducción de una canción, 20 centavos, pero cambian la comisión por ingresar a la plataforma. La primera plataforma digital, otorga una comisión de 50 pesos, realiza los cálculos para conocer las ganancias semanales por 300, 600 y 900 reproducciones.
En este primer caso, la expresión algebraica es y = 0.20x + 50; es decir, para obtener las ganancias semanales, debes multiplicar los 20 centavos por el total de reproducciones y sumarle la comisión semanal que es de 50 pesos. Al realizar los cálculos, obtienes que por 300 reproducciones se obtiene un total de 110 pesos. Por 600, la ganancia es de 170 pesos y por 900 reproducciones se otorgan 230 pesos.

Bien, la segunda plataforma digital da una comisión de 150 pesos a la semana, y paga los mismo 20 centavos por reproducción, revisa qué ganancias se obtienen:
La expresión algebraica es y = 0.20x + 150.
Al sustituir “x” por sus valores numéricos, se ve que, por 300 reproducciones, la ganancia es de 210 pesos; por 600 reproducciones, obtienen 270 pesos en total y, cuando la melodía alcanza 900 reproducciones, se pagan 330 pesos.

Como puedes ver, esta plataforma digital de contenido auditivo otorga una mayor cantidad de comisión a la semana. Calcula las ganancias en una tercera plataforma, donde pagan lo mismo por reproducción (0.20 pesos) y de comisión dan $350. En este caso, la expresión algebraica es y = 0.20x + 350. Ahora, al resolver las operaciones verás que, por 300 reproducciones la ganancia es de 410 pesos; por 600, se otorgan 470 pesos y por 900 reproducciones, se ganan 530 pesos en una semana.

¿Cómo piensas que serán las rectas de las gráficas? ¿En qué se parecen? ¿Cuál tendrá mayor pendiente?
Analiza las rectas y fíjate cuál le corresponde a la plataforma 1, cuál a la 2 y cuál a la 3.
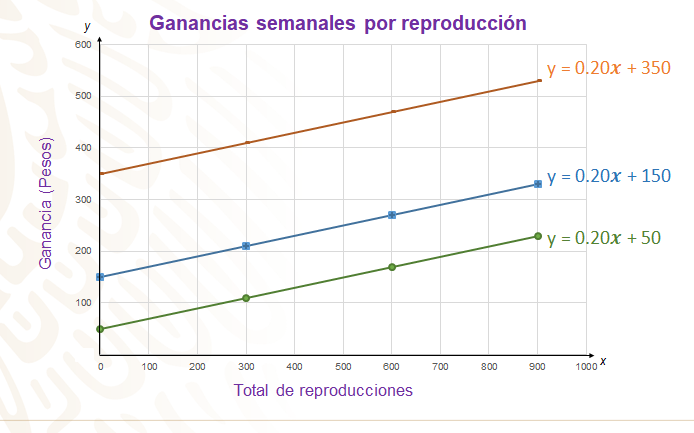
Analiza detenidamente las gráficas. ¿Ya sabes qué recta corresponde a cada plataforma?
La recta en color verde representa a la plataforma 1 y su expresión algebraica es y=0.20x+50; la recta azul corresponde a la plataforma 2 y su expresión algebraica es y=0.20x+150; y la recta color anaranjado corresponde a la plataforma 3, que da una comisión semanal de 350 pesos, su expresión algebraica es y=0.20x+350.
En este caso, puedes observar que las rectas son paralelas; es decir, tienen la misma pendiente, ya que el valor de “a” o la razón de cambio es la misma en los tres casos, 20 centavos por reproducción.
¿Pero qué diferencia hay entre este conjunto de rectas y las que analizaste anteriormente?
Para poder observarlo mejor, se presentarán juntos, ambos planos.
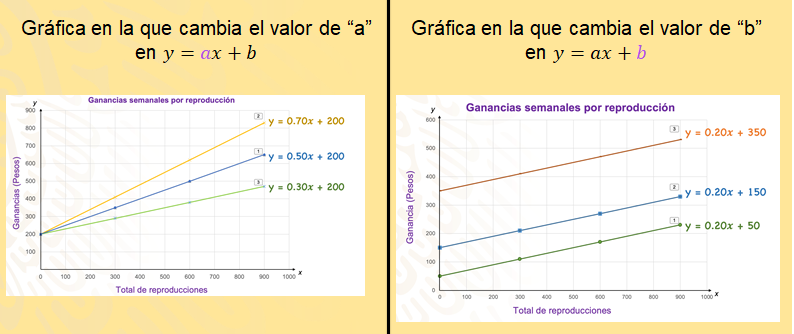
Del lado izquierdo, puedes observar las primeras gráficas. En estos casos, en la expresión algebraica cambia el valor de la literal “a” y “b” tiene el mismo valor; del lado derecho, observa las rectas en las que en su expresión algebraica cambia “b” y “a” es la misma constante en los tres casos.
Como puedes ver, cuando el valor de “a” cambia, la inclinación o pendiente se modifica manteniendo b constante, pero cuando el valor de “b” varía, el punto en donde la recta intersecta al eje “y” se modifica manteniendo a “a” constante.
Ya has visto la relación que hay entre las expresiones algebraicas de la forma y=ax+b y su gráfica; la relación de las literales “a” y “b”, respecto a la pendiente y el punto donde se intersecta al eje “y”.
A continuación, se presentará una gráfica y tú revisarás cuál de las expresiones algebraicas que se presentan es la que le corresponde a cada recta.

Se plantearán algunas preguntas para guiarte. La primera es: ¿Cuál es la diferencia entre las rectas? En las expresiones algebraicas que observas, ¿cuál es el valor que cambia: “a” o “b”?
Tienes que la pendiente de la recta es diferente y ambas intersectan en el mismo punto al eje de las ordenadas, en la coordenada (0, 20); donde el valor “y” del par ordenado, corresponde al valor de “b”. Analiza el valor de “a” en cada caso.
¿Cuál es mayor? ¿Cuál de las rectas presenta mayor inclinación hacia el eje de las ordenadas?
Por la pendiente, se puede decir que la literal “a” tiene mayor valor en la gráfica amarilla. Por lo tanto, la expresión y=10x+20 corresponde con la recta de color azul y la expresión y=25x+20 corresponde a la recta de color amarillo, ya que el valor de “a” es mayor, lo que significa que la pendiente es mayor.
Revisa un par de rectas más. Se te invita a que las analices cuidadosamente y, al igual que en la actividad anterior, identifiques cuál es la expresión algebraica que corresponde a cada recta.
Observa las siguientes gráficas, ¿en qué se parecen?, ¿en qué difieren?
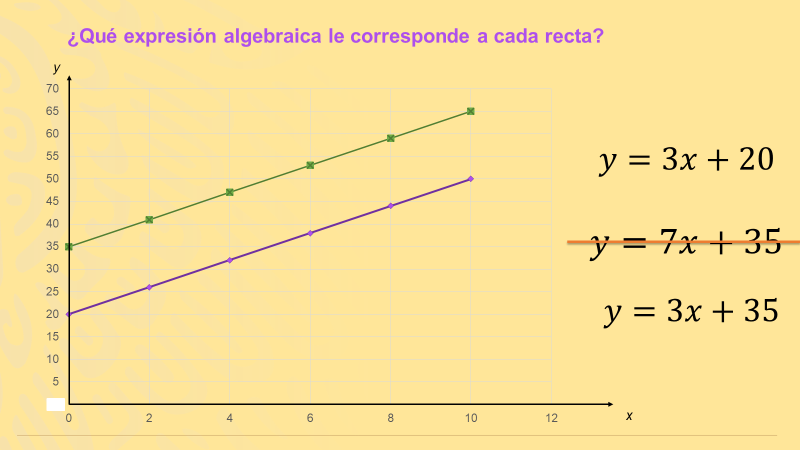
Como puedes ver, las gráficas están representadas por rectas paralelas, debido a que la razón de cambio es la misma, por ello tienen la misma pendiente; entonces, se puede afirmar que la expresión algebraica y=7x+35, no corresponde a ninguna de las rectas, ya que el valor de “a” tiene que ser el mismo en ambas expresiones.
Ahora, ¿cuál es la expresión algebraica que corresponde a la recta de color verde?
La expresión es y=3x+35 ya que, el valor que corresponde a “b” determina el punto donde la recta se cruza con el eje de las ordenadas. En este caso, el valor de “b” es 35, justo el punto de intersección de la recta verde con el eje “ye”. Pero analiza el valor de “b” en la expresión y=3x+20. Efectivamente, la recta se intersecta con el eje de las ordenadas en la coordenada (0, 20).
El reto de hoy:
Se te invita a que pienses en una situación similar a las que se presentaron en esta sesión, en la que tengas que comparar la razón de cambio o la ordenada al origen para comparar las gráficas correspondientes.
Recuerda que éste es un material de apoyo y que, en tu libro de texto de Matemáticas, puedes encontrar más información y actividades de relaciones con variación lineal, que puedes resolver.
¡Buen trabajo!
Gracias por tu esfuerzo.