Perímetro y área
Perímetro y área
Aprendizaje esperado: calcula el perímetro de polígonos y del círculo, y áreas de triángulos y cuadriláteros desarrollando y aplicando fórmulas.
Énfasis: usar expresiones algebraicas equivalentes para representar el perímetro y área de figuras geométricas.
¿Qué vamos a aprender?
Estudiarás el aprendizaje esperado: “Calcula el perímetro de polígonos y del círculo, y áreas de triángulos y cuadriláteros, desarrollando y aplicando fórmulas.”
Aprenderás cómo usar expresiones algebraicas equivalentes, para representar el perímetro y área de figuras geométricas.
¿Qué hacemos?
No cabe duda de que las matemáticas están presentes en muchas situaciones de la vida cotidiana.
La construcción es fundamental en el desarrollo social y conocer sobre las distintas formas geométricas y sus medidas, así como el perímetro y el área, es muy importante.
La forma de medir ha cambiado a lo largo del tiempo, pero la necesidad de hacer mediciones sigue existiendo; dado que, en toda actividad humana, se requieren mediciones de algún tipo. Presta atención al siguiente audiovisual.
Observa del minuto 00:47 al 02:22 y del 03:39 al 05:21.
- Obtención del perímetro en la antigüedad
https://youtu.be/CpkAppRUgoU
En la actualidad, existen técnicas de medición modernas, con instrumentos muy precisos. ¿Qué instrumentos conoces que se usen para medir? Tal vez el instrumento para la medición del perímetro más común, en este contexto, sea el flexómetro.
Observa el siguiente ejemplo.
En una secundaria, se va a reforestar un espacio que tiene forma de hexágono irregular, como la que se muestra en la imagen. En todo el contorno, se va a colocar una cerca de metal. ¿Cuál es el perímetro de la figura si, con el flexómetro, se obtuvieron las medidas descritas?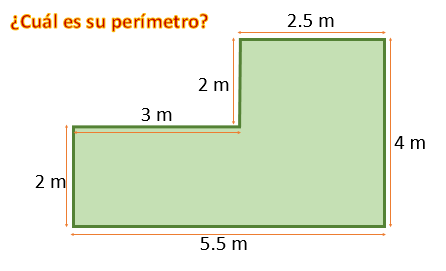
El perímetro se calcula sumando la longitud de todos los lados de una figura. En este caso, son seis lados; así que se puede escribir la expresión: perímetro es igual a lado 1, más lado 2, más lado 3, más lado 4, más lado 5, más lado 6; que, al sustituir por los valores que se obtuvieron en la medición, resulta un perímetro igual a dos, más tres, más dos más, dos puntos cinco, más cuatro, más cinco puntos cinco; lo que es igual a 19 metros.
De manera general, se puede expresar que: el perímetro de cualquier figura es la medida de la longitud alrededor de ella. En un polígono, el perímetro es la medida de la longitud total que suman todos sus lados. En un círculo, el perímetro es la la longitud de la circunferencia que lo rodea; entonces el perímetro delimita a una figura.
A lo largo de sesiones anteriores de matemáticas, aprendiste algunas fórmulas para el cálculo del perímetro de diversas figuras. Estas fórmulas incluyen literales y números.
Por ejemplo, la fórmula para calcular el perímetro de un cuadrado es p=l+l+l+l; donde “p” representa el valor del perímetro y “l” representa la longitud de cada uno de sus lados, que también es equivalente a la expresión p=4l, o bien p=4 por “l”, pues se conoce que un cuadrado tiene la misma longitud en cada uno de sus lados.
De hecho, estas fórmulas son expresiones algebraicas. Una expresión algebraica es una combinación de literales (letras que sirven para representar cantidades) y números que, en algunos casos, representan coeficientes (números junto a las letras) que las multiplican.
Por ejemplo, en la expresión algebraica para encontrar el perímetro del cuadrado p = 4ele, el coeficiente cuatro multiplica a la literal ele.
Un rectángulo es un cuadrilátero, cuyos lados forman ángulos rectos. A diferencia del cuadrado, no todos los lados son iguales entre sí. Existe igualdad de longitud sólo en los lados que son opuestos entre sí.
Es posible representar esta característica asignando una literal a cada lado, tal como aparece en la figura.
En este caso, se usa la literal “b” para representar la longitud de la base y se usa la literal “a” para representar la longitud de la altura.
Sin embargo, pueden utilizarse otras literales como “x” o “y”, tal y como se aprecia en esta figura.
Entonces, utilizando la fórmula del perímetro del rectángulo, analiza las siguientes expresiones algebraicas equivalentes:
A partir de la expresión p = a + a + b + b, es posible agrupar términos semejantes y obtener la expresión: p = (a + a) + (b + b), que es equivalente a la expresión p = 2a + 2b.
Por otro lado, usando un orden diferente de la misma expresión, puede representarse como: p=a+b+a+b; aquí, es posible agrupar p=(a+b)+(a+b), que es equivalente a p=2(a+b). Al aplicar la propiedad distributiva de la multiplicación, obtienes la expresión inicial: p = 2a + 2b.
Esto no es algo nuevo para ti, ya has usado este tipo de expresiones antes. Generalmente, sustituyen un valor conocido en dos de las literales de la expresión, para conocer la tercera.
Por ejemplo, si la base del rectángulo mide 5 cm y la altura mide 8 cm; entonces, sustituyendo estos valores en la expresión p=2(a+b), donde “p” es el perímetro, “b” es la base y “a” la altura, encuentran que “p” es igual a dos veces la suma de la base más la altura; es decir, p = 2 por la suma 8 + 5, que es igual a 2 por 13, igual a 26 cm. Las unidades son lineales porque se trata de una longitud, la longitud del contorno del rectángulo.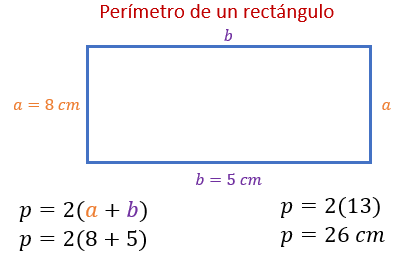
Si sustituyes a las literales en cualquiera de las otras expresiones por los mismos valores, el resultado sería el mismo; con lo que se comprueba de forma numérica que las expresiones algebraicas son equivalentes.
¿Qué sucedería si, en lugar de tener números para sustituir en las literales, se tienen otras expresiones algebraicas?
Observa el siguiente audiovisual que resume lo que has visto hasta ahora y que propone un ejemplo para responder a la última interrogación.
Observa del minuto 00:31 al 02:41 - Expresiones algebraicas para calcular
https://youtu.be/GFuDLEedxpY
El perímetro de este rectángulo está dado por la expresión p=26m+12. El valor de “m”, puede ser sustituido por un número o por otra expresión algebraica; entonces, eventualmente, podría conocerse un valor numérico final para “p”.
Realiza otro ejercicio para consolidar este aprendizaje. En un salón de clases, un equipo que expuso sobre nutrición, quiere pintar el triángulo de una dieta balanceada, en una de las paredes de su escuela.
Observa el triángulo que aparece en la figura.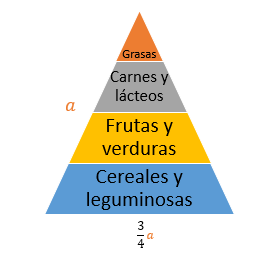
El equipo necesita cinta para delimitar el perímetro y que, al momento de pintarlo, quede un triángulo bien delineado. Sólo cuentan con 3.85 metros de cinta. Desean trazar un triángulo isósceles cuya longitud, del lado desigual, sea tres cuartas partes de la longitud de uno de los lados iguales.
Primero, es necesario determinar la expresión que describa cuál será el perímetro de dicho triángulo. Posteriormente, deben determinar la longitud de los lados que les permita aprovechar al máximo la cinta que tienen y, finalmente, deben identificar si es posible pintar ese triángulo en un área de la pared que tiene 2 metros de largo por 2 metros de alto.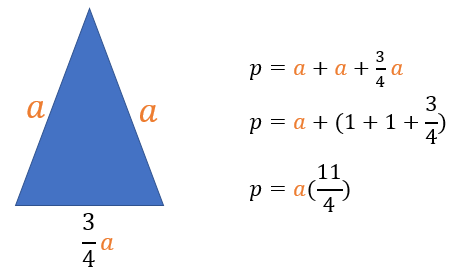
Para determinar la expresión del perímetro del triángulo asociado, puedes asignar literales a los lados. A los lados iguales del triángulo los representaremos con la literal “a”. Por otra parte, como el lado desigual es tres cuartos de la longitud de uno de los lados iguales, entonces, se representa con la expresión tres cuartos de “a”. De esta manera, el perímetro del triángulo queda determinado por la expresión p=a+a+(3/4)a
Al sumar los términos semejantes, es posible determinar que p=a(1+1+(3/4))
De manera que p=a(11/4)
Para saber el valor de “a”, tal que el perímetro del triángulo sea de 3.85 m de longitud, se procede a despejar “a” y luego a sustituir el valor de “p”=3.85
a=p/(11/4), lo que es equivalente a la expresión a=(4/11)p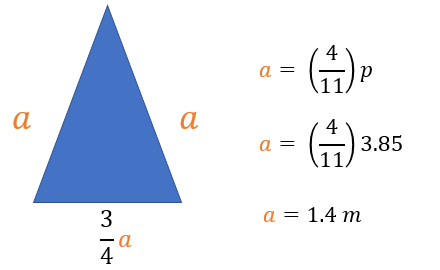
Al sustituir “p” por 3.85, resulta: a=(4/11) por 3.85; lo que es igual a 1.4 Por lo tanto, el valor de cada uno de los lados iguales del triángulo debe ser de 1.4 metros.
Si se sabe que “a” vale 1.4 metros, ¿cómo calculas la longitud del lado desigual?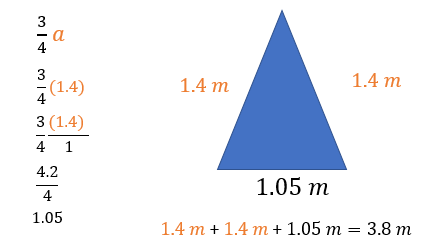
Para determinar el lado desigual, simplemente se multiplica el valor de “a” por tres cuartos; en este caso, tres cuartos por 1.4, al ser una fracción, multiplicas tres por 1.4 que es igual a 4.2 y cuatro por uno, lo que resulta 4. Finalmente, divides 4.2 entre cuatro; y, así, obtienes 1.05 metros. De esta forma, puedes conocer que los lados miden: 1.05 metros, 1.4 metros y 1.4 metros. Es posible observar que la suma de las tres longitudes efectivamente es de 3.85 m
Ya conocemos las medidas de los lados del triángulo; ahora ¿cómo sabes si el triángulo se puede trazar en una pared de dos metros de alto?
Dado que la altura de un triángulo no puede ser mayor al lado más largo del triángulo y, como el lado más largo mide 1.4 m; entonces, es posible trazar el triángulo en una pared de 2 m de alto. Ahora, con respecto al largo, la base del triángulo, mide 1.05 metros, que cabe sin problemas en los 2 metros disponibles.
Hasta ahora, has aprendido a usar expresiones algebraicas equivalentes para representar el perímetro; es momento de analizar el área de las figuras geométricas usando expresiones algebraicas.
El área indica todo lo que queda entre los lados de una figura; es decir, la superficie delimitada por su perímetro. Para medir el área, se utilizan unidades cuadradas como el centímetro cuadrado, el metro cuadrado, etcétera. Presta atención a lo siguiente.
Observa el video del minuto 01:00 al 02:31. - Figuras geométricas y expresiones equivalentes
Presten atención a la situación que se plantea en la siguiente cápsula y escribe en tu cuaderno una expresión algebraica que exprese el área del rectángulo verde.
Observa el mismo video del minuto 03:09 al 03:32
Observa que la altura del rectángulo mide “z”, la base del rectángulo completo mide “x”, mientras que la base del rectángulo rosa mide 4; entonces, si a la base del rectángulo completo, “x”, se le resta la base del rectángulo rosa, “4”, se obtiene la base del rectángulo verde; así, “x menos 4” de base y “z” de altura. Considera que todas las medidas son en metros.
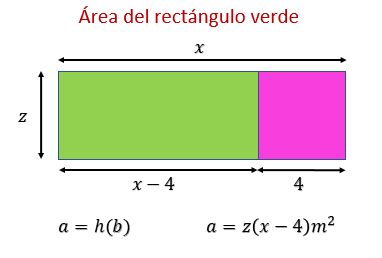
Sustituye los valores en la fórmula del área del rectángulo a = h por b y obtienes a= z por x-4
La expresión algebraica “a” = “z” por “x” menos 4, ¿coincide con tu respuesta?
Si al rectángulo completo le quitas el rectángulo rosa, queda sólo el rectángulo verde; entonces, para encontrar el área del rectángulo verde, puedes restar las áreas.
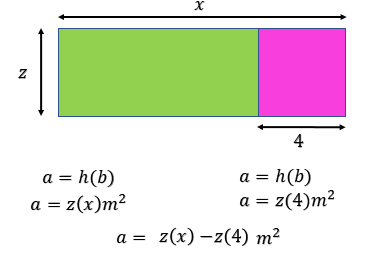
Para el rectángulo completo, tienes una base “x” y una altura de “z”; sustituyendo los valores en la fórmula para calcular el área del rectángulo, se tiene que el área es “z” por “x” metros cuadrados. Para el rectángulo rosa, la base es 4 y la altura “z” que, al sustituir en la fórmula, se obtiene: área es igual a “z” por cuatro metros cuadrados. Por último, calcula la diferencia de las áreas, quedando: área es igual a “z” por “x” menos “z” por cuatro metros cuadrados.
La expresión algebraica “a” es igual a “z” por “x” menos “z” por cuatro metros cuadrados, ¿coincide con tu respuesta? Se puede afirmar que cualquiera de las dos es correcto, ya que se trata de expresiones algebraicas equivalentes y, como ambas expresiones corresponden al área del rectángulo verde, deben ser iguales.
La expresión que obtuvo el profesor Jared fue “a” igual a “z” por “x” menos cuatro, metros cuadrados; y la que obtuvo Lety fue, “a” igual a “z” por “x” menos “z” por cuatro, metros cuadrados.
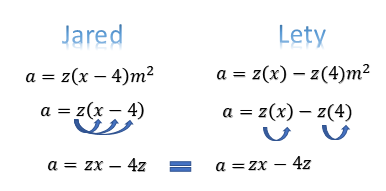
Observa, en la expresión que obtuvo el profesor Jared que, al eliminar paréntesis, se tiene “z” por “x”, “zx” menos “z” por cuatro, cuatro “z”. En el caso de la expresión que obtuvo Lety encontró “z” por “x” “zx” menos “z” por 4, “4z”; con lo cual, las expresiones son iguales.
Y con esta comprobación se puede afirmar que “a” = “z” por “x” menos 4 y “a” es igual a “z” por “x” menos “z” por cuatro, son expresiones algebraicas equivalentes.
El reto de hoy:
Si tienes alguna duda, puedes solicitar a tus maestras o maestros a distancia, que te pongan más ejercicios de este tipo.
Ubica en tu libro este tema. Resuelve todo lo que puedas para practicar. Tal vez encuentres formas diferentes para realizar estos cálculos. Anota tus dudas y recuerda que también puedes pedir ayuda, y retroalimentación a distancia, de tus maestras o maestros, cuando sea posible.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa*
Para saber más:
Lecturas