Sucesiones especiales

Sucesiones especiales

Aprendizaje esperado: identifica y aplica la regularidad de sucesiones con figuras, que tengan progresión aritmética o geométrica, así como sucesiones especiales.

Énfasis: identifica la regularidad de una sucesión especial y la utiliza para encontrar términos que continúan la sucesión.

¿Qué vamos a aprender?

Identificarás y aplicarás la regularidad de sucesiones con figuras, que tengan progresión aritmética o geométrica, así como sucesiones especiales, de igual manera, identificarás la regularidad de una sucesión especial y la utilizarás para encontrar términos que continúan la sucesión.

¿Qué hacemos?

Identificarás la regularidad de una sucesión especial y la utilizarás para encontrar los términos que continúan la sucesión. Te preguntarás, ¿Qué son las sucesiones con progresión especial? Recuerda que ya trabajaste algunas sucesiones e identificaste su regularidad y el tipo de progresión que tienen, incluso aprendiste algunas sucesiones especiales.

Las sucesiones especiales son aquellas en que la regularidad que siguen no implica aumentar o disminuir un valor constante, como ocurre con las sucesiones con progresión aritmética o geométrica, ni tampoco tienen un crecimiento o decremento geométrico constante.

Con este antecedente continuarás haciendo análisis de la regularidad, pero ahora lo harás para las sucesiones con progresión especial, a fin de identificar el patrón que permite saber cómo se construyen sus términos.

Recuerda que puedes encontrar o reconocer en tu entorno el uso de patrones que no son sucesiones aritméticas o geométricas, por ejemplo, en la cultura puedes encontrar diferentes ejemplos de esos patrones y de su aplicación.

En el huipil, que es una de las prendas femeninas más antiguas del país. Su nombre deriva de la voz náhuatl huipilli, que quiere decir: “vestido o blusa adornada”. Es usado a lo largo y ancho del país, por lo cual tiene distintas características de acuerdo con cada región, pero si observas bien la parte inferior, verás que los bordados forman un patrón de figuras.

Se puede observar que la parte superior e inferior o todo el huipil es ornamentado con figuras que se repiten. Los bordados que tiene cada huipil retoman elementos característicos que representan a los grupos indígenas, en muchos casos, sus bordados tienen motivos geométricos.

Allí puedes ver las matemáticas aplicadas. Trata de encontrar patrones matemáticos, en particular, geométricos. Inicia la búsqueda.

Observa las siguientes imágenes.

La talavera es un tipo de mayólica loza común con esmalte metálico proveniente de los estados de Puebla y Tlaxcala. Los colores empleados en su decoración son el azul, amarillo, negro, verde, naranja y malva. Cada pieza está hecha a mano en torno, su terminación de vidriado contiene estaño y plomo, y se fabrican de esa manera desde la época virreinal.

Obsérvalas bien. ¿Ya encontraste elementos matemáticos? Seguramente estás empezando a darte cuenta de la relación que tienen todas estas artesanías con el tema de hoy. Observa otros ejemplos.

En la imagen puedes observar cómo algunos sombreros de fibras naturales que son tejidos por hombres, mujeres, niñas y niños, son hechos con paja y otros con palma, entre otras fibras. Observa el diseño de cada uno.

Para elaborar las artesanías se invierte tiempo, esfuerzo, creatividad y conocimiento por parte de las personas.

Ahora, puedes decir, con base en todo lo observado en las imágenes que acabas de ver, ¿Qué relación o aplicación de algunos aspectos de la matemática identificaste? ¿Qué relación encuentras con el contenido de hoy?

Cuando veías las imágenes seguramente pudiste recordar que has trabajado con sucesiones de figuras, y estas sucesiones siguen una regla o patrón.

En todas las artesanías vistas había sucesiones de figuras geométricas, o simplemente imágenes o figuras que se repetían pero que seguían un patrón.

Las sucesiones de figuras que acabas de observar son sucesiones especiales, porque no siempre vas a encontrar un único valor constante que aumente o disminuya entre un término y otro de la sucesión, ni tampoco que la razón entre los términos sea un valor constante.

Además, no debes perder de vista que cada objeto tiene la creatividad única de los artesanos que las realizan a mano, bien sea bordado, tejido o pintado, genera una sucesión especial y muchas de ellas son únicas.

Por eso puede decirse que, desde hace muchos años, se usan sucesiones especiales para decorar.

En resumen, las sucesiones especiales son aquellas en las que no hay una constante aditiva entre dos términos consecutivos, ni una constante multiplicativa, como sucede con las sucesiones aritméticas o geométricas, respectivamente.

Recuerda que trabajaste con esas sucesiones y analizaste algunas en el libro de texto. Es momento de trabajar las sucesiones especiales que están propuestas en la página 144 donde está el Desafío 78 “Números figurados”.

https://libros.conaliteg.gob.mx/P6DMA.htm?#page/144

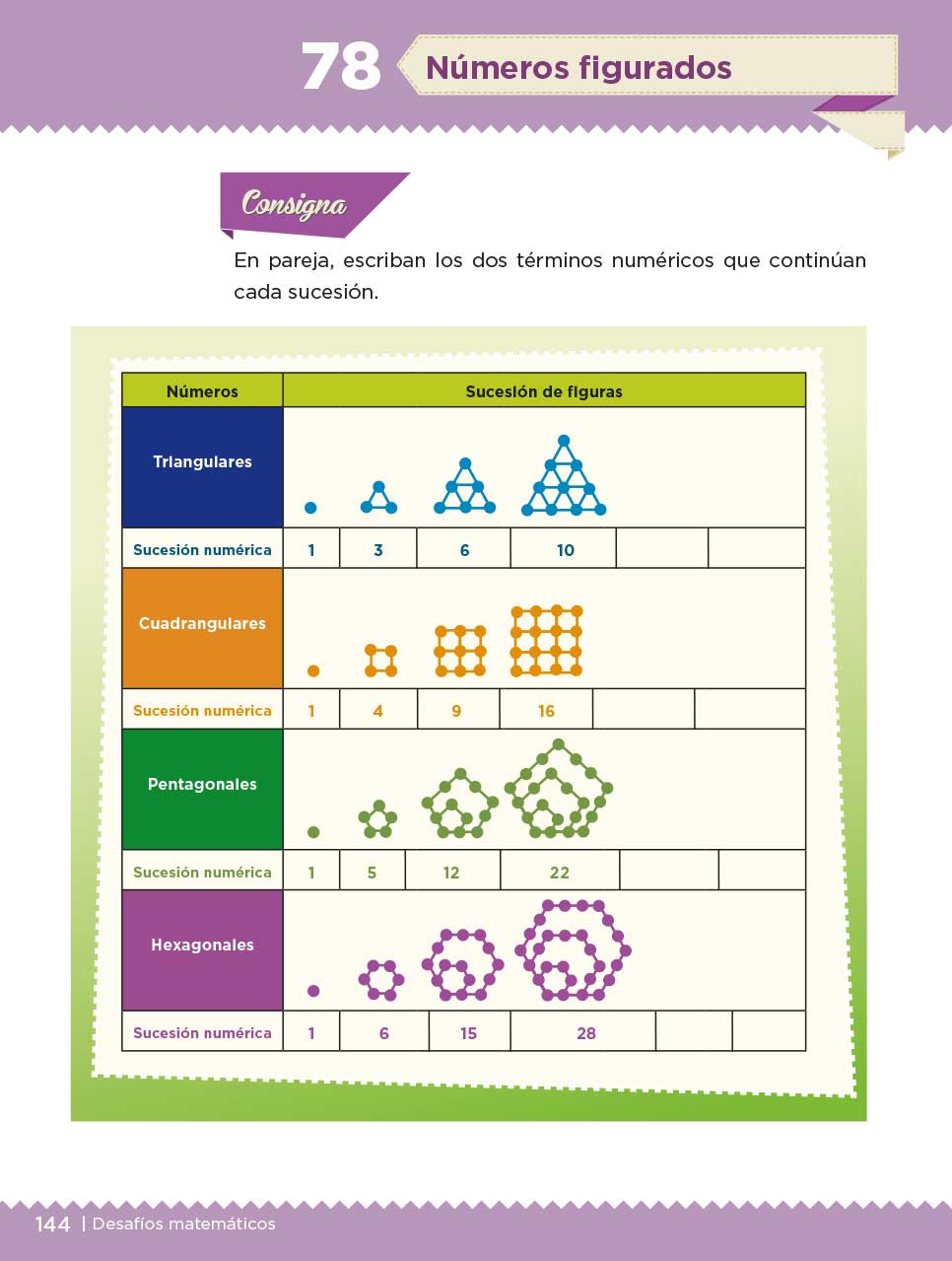
La consigna dice: En parejas escriban los dos términos numéricos que continúan la sucesión.

Observa detenidamente la imagen que te presentan. ¿Qué observas? Es una tabla que tiene dos columnas. En la primera columna tiene como título números y, en la segunda, sucesión de figuras. En la tabla, se observan sucesiones representadas de forma gráfica y debajo de la figura, en el siguiente renglón, la misma sucesión, pero ahora expresada con números.

Analiza la primera sucesión y busca encontrar la regularidad con la que va creciendo cada término, tanto de manera gráfica como numérica. Estos dos análisis te pueden ayudar a encontrar una respuesta, empieza con la primera sucesión.

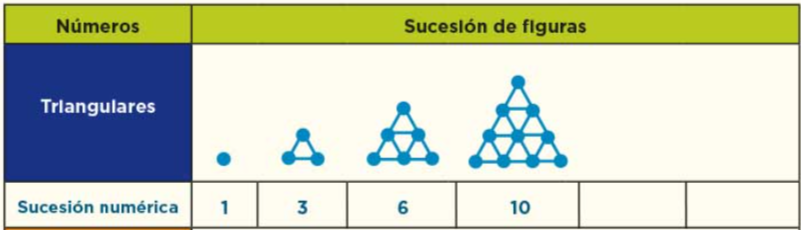
Esta sucesión es conocida como sucesión de números triangulares. Observa que las figuras de la sucesión son triángulos, pero ¿La sucesión de números corresponde con la cantidad de triángulos que aparece en cada figura? Observa los números y las figuras, ¿A qué corresponde la representación numérica que está debajo de la imagen? No parece responder a la cantidad de triángulos, porque la primera figura no es un triángulo sino un punto. Analízala con detenimiento y trata de identificar cuál es la relación con la sucesión numérica.

¿Ya la encontraste? Es con respecto al número de puntos que se encuentran en los vértices de los triángulos. Explica por qué consideras que la sucesión numérica corresponde con el número de puntos, porque observaste los números. La primera figura de la sucesión inicia con un punto y, en la sucesión numérica está el número uno. La siguiente figura tiene tres puntos y es el mismo número que aparece en la sucesión numérica.

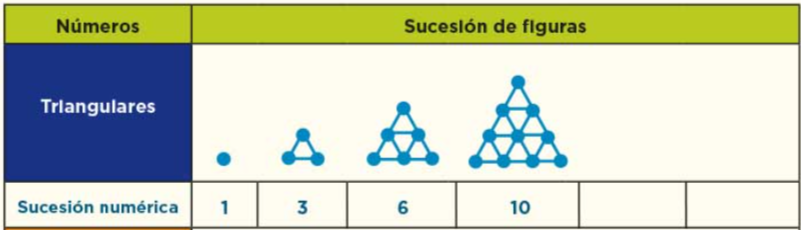
Observa, ¿Qué sucede con la figura que sigue en la sucesión? ¿Cómo aumenta? ¿Se tienen que aumentar dos puntos para formar la segunda figura? No, la siguiente figura tiene 6 puntos entonces si el primer triangulo se formó con tres puntos, para la siguiente aumentó 3 puntos. ¿Observas la forma de la figura en general? ¿Al aumentar los puntos se transforma la forma de la figura? Pues no. No cambia su forma, sigue siendo un triángulo grande formado con triángulos pequeños en su interior. Así es, se sigue conservando la figura exterior en forma de triángulo, lo cual puedes comprobar con las siguientes figuras conforme las vayas construyendo. En todas continúan siendo un triángulo, observa cómo va el aumento de puntos.

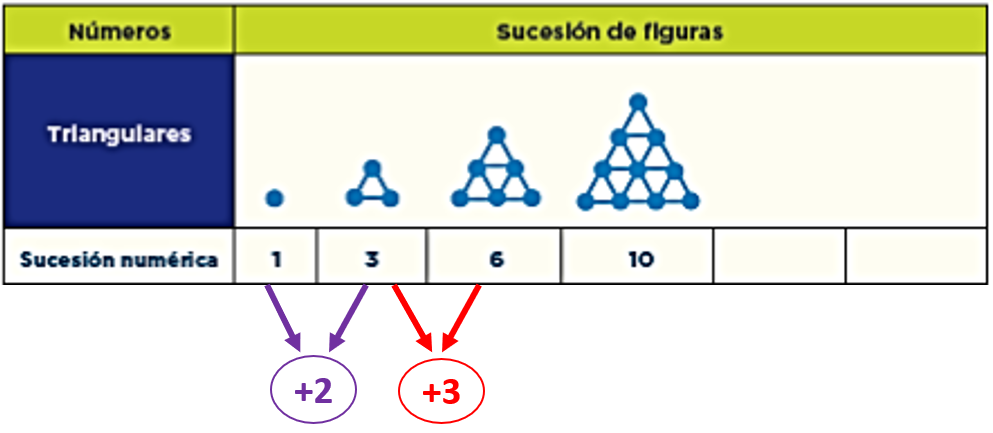
Para ello, coloca en la parte inferior el número que indica el aumento de puntos entre un término y otro consecutivo de la sucesión. Nota que del primer punto al primer triangulo, se añaden dos puntos; para la siguiente figura, se aumentaron tres puntos. Continúa anotado cómo va el crecimiento de la sucesión.

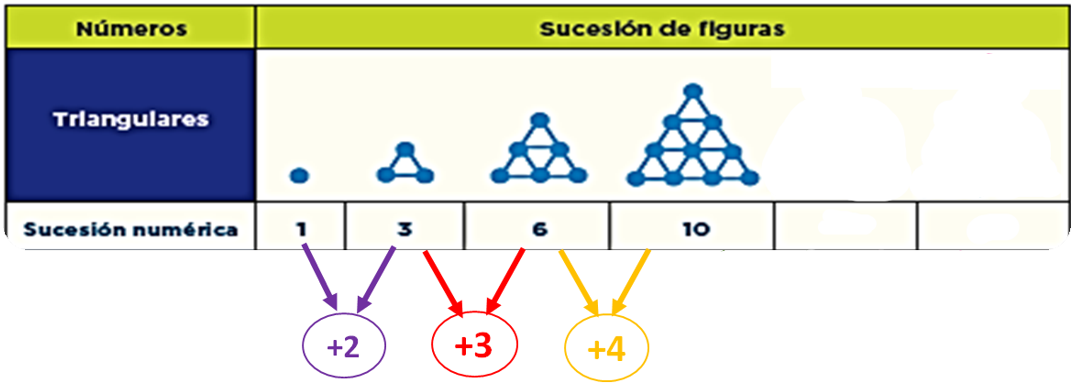
Para la figura tres aumentó 3 puntos más. Para la 4, aumentó 4 puntos. Sigue analizando cómo aumenta de una figura a otra para encontrar las dos figuras que corresponden a los términos siguientes de la sucesión.

Pon atención, el primer incremento fue 2 para la siguiente aumentó 3 después aumentó 4. ¿Ya lo entendiste? Para la figura 5 aumentará 5 puntos.

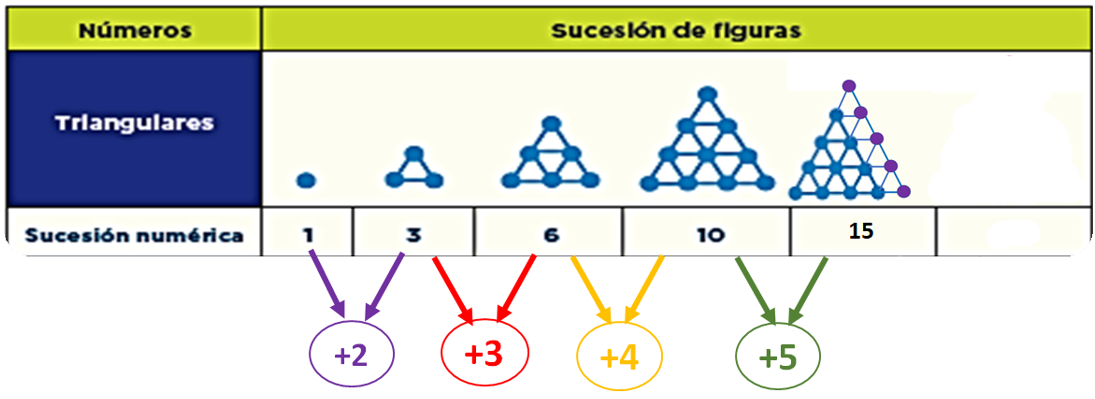
Y en la siguiente figura, la seis, serán 6 puntos más, así ya encontraste la regularidad de la sucesión. Esa regularidad representa el patrón o regla entre los términos consecutivos de la sucesión; te dice cómo se incrementa de término a término. Te indica cómo se está construyendo la sucesión conforme se incrementan los puntos.

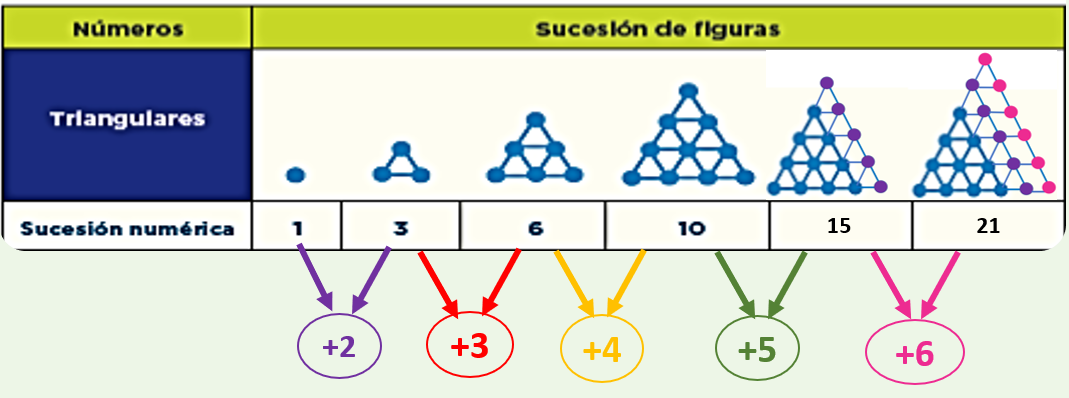
El patrón o regla da la pauta para identificar cuál es el tipo de progresión de la sucesión, tanto de figuras como numérica. Ahora bien, ¿Cómo quedarían las figuras? Definitivamente tienen que ser triángulos más grandes porque la sucesión está respetando esta forma a partir de la segunda figura, aunque vaya creciendo, siguen siendo triángulos.

Realiza las figuras en tu libro para comprobar si los números que encontraste son correctos y se puede respetar la forma triangular de la sucesión. Intenta la representación gráfica.

¿Ya tienes la sucesión completa? siguiendo la estrategia que encontraste se formaron las siguientes figuras respetando el patrón que sigue la sucesión. Descubriste que la regularidad era que los números aumentaban una unidad a partir del 2 de modo que en cada figura consecutiva se incrementa 3, 4, 5, y 6 puntos.

Estos valores ya los habías obtenido antes. Recuerda, los analizaste en la sucesión de figuras formadas con los cerillos y corresponde con la sucesión numérica que se genera con el número de cerillos que se añaden para formar las figuras. Si recuerdas, son figuras completamente diferentes, pero las sucesiones numéricas son iguales.

Analiza la tercera sucesión. Hay una propuesta de patrón o regularidad para la tercera sucesión, de acuerdo con las cuatro figuras o términos que se presentan, todas respetan la forma del pentágono. Muy bien, ¿Ya tienes la regularidad entre una figura y otra? Por favor anótala para que puedas verificarla. ¿Qué figura se estará formando en cada nuevo término de la sucesión?

Se forma un nuevo pentágono, sólo que más grande, al analizar la sucesión entre las dos primeras figuras, el aumento es de 4 puntos, después, entre las siguientes dos, de 7 puntos; luego, 10 puntos, y así seguirá. Si no puedes encontrar la regularidad en la sucesión de números toma la opción de dibujar la siguiente figura.

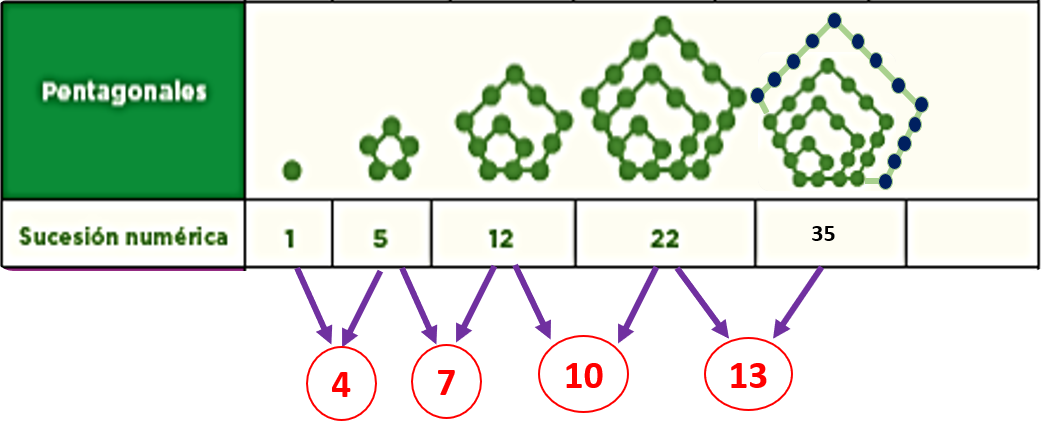
Para formar el pentágono de la figura 5, debiste aumentar 13 puntos, es decir, se agregaron otros tres puntos al número de puntos que agregaste para formar la figura 4 entonces, la sucesión está formada por los siguientes números: 1, 5, 12, 22, 35. ¿Ya tienes el siguiente número de puntos que se deberán agregar para formar la figura 6?

Para formar la última figura de esta sucesión, sólo debes sumar 16 puntos a la figura 5. En otras palabras, el patrón consiste en ir sumando 3 unidades al número de puntos de la figura anterior, salvo en el caso de la primera, en la que se suman cuatro unidades, efectivamente así es como se forma la sucesión de números pentagonales.

Analiza la segunda sucesión de figuras. Como podrás observar, se trata de una sucesión de números cuadrangulares y como en los casos anteriores, la regularidad se puede observar, a partir del número de puntos que aumentan de una figura a la otra.

Estudia el comportamiento de esta sucesión. De la primera a la segunda figura, se añadieron 3 puntos, así que la figura 2 está formada por cuatro puntos. Luego, para formar la tercera figura se sumaron 5 puntos más; la siguiente figura, aumentó 7 puntos. ¿Ves que todos son números impares?, lo que quiere decir que el número que sigue es el 9

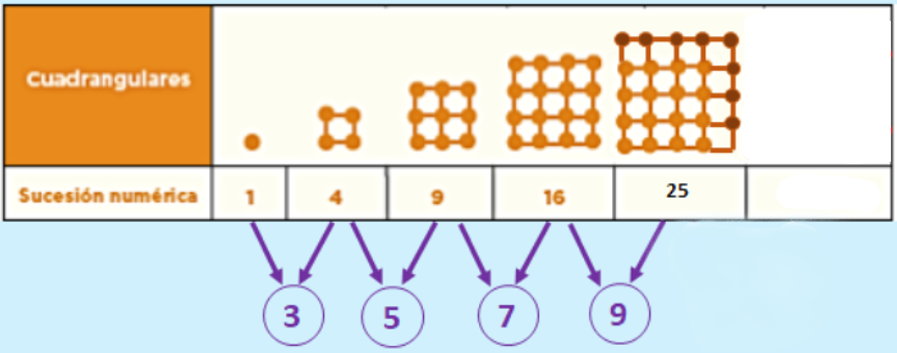
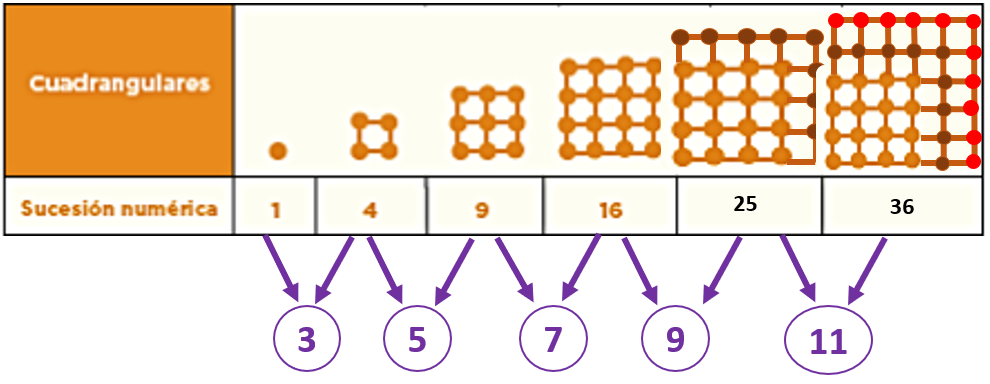
De esta manera se puede identificar la regularidad que sigue la sucesión de puntos que se agregan para formar la sucesión de figuras cuadrangulares, la cual se puede comprobar al realizar el acomodo de puntos. Observa que, de nuevo, se conserva la figura de un cuadrado en cada uno de los términos consecutivos de la sucesión.

Y para completar la sucesión de números cuadrangulares, sólo basta sumar 11 a la figura 5 para construir la última figura.

Ahora completa la sucesión de figuras hexagonales de tu libro de texto, aplica lo que hoy aprendiste al buscar y encontrar la regularidad o patrón para formar las sucesiones especiales que acabas de realizar. Considera que estas sucesiones tienen un nivel de complejidad más alto de lo que habías hecho hasta ahora. El nivel de complejidad de los contenidos siempre va en aumento.

Como cierre de este tema debes destacar que una manera de clasificar las sucesiones de figuras y de números es a partir de la diferencia que hay entre los términos consecutivos.

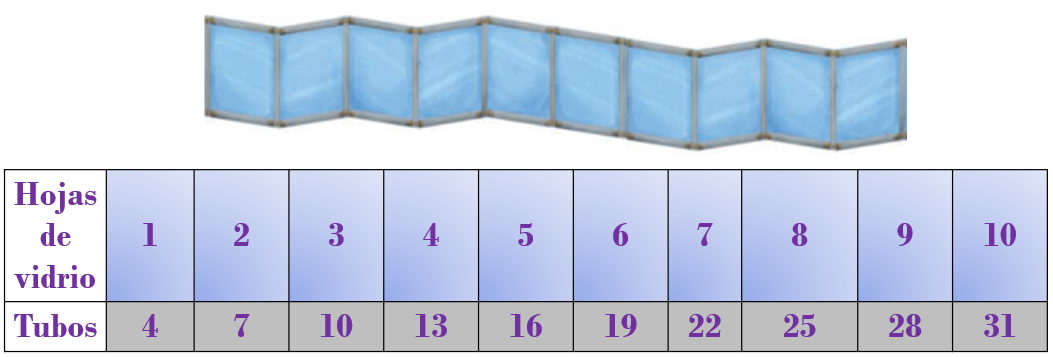
Puedes observar que:

• Si la diferencia entre los términos consecutivos es el mismo valor, entonces se trata de una constante aditiva y la sucesión tiene una progresión aritmética.
• Si la diferencia no es constante, pero el cociente entre los términos consecutivos es una constante, significa que tienen la misma razón y, entonces la sucesión tiene progresión geométrica.
• Cuando la diferencia entre los términos consecutivos no es constante ni la razón entre los términos consecutivos es constante, entonces es una sucesión con progresión especial.

El reto de hoy:

Revisa los ejercicios que hiciste y elige uno que puedas compartir con algún familiar cercano, explícale como pudiste obtener tus resultados.

Si te es posible, consulta otros libros o materiales para saber más sobre el tema.

¡Buen trabajo!

Gracias por tu esfuerzo.

*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/20/P6DMA.htm