Rectas paralelas y ángulos
Rectas paralelas y ángulos
Aprendizaje esperado: analiza la existencia y unicidad en la construcción de triángulos y cuadriláteros, y determina y usa criterios de congruencia de triángulos.
Énfasis: aplicar la relación entre rectas paralelas cortadas por una transversal para justificar la suma de ángulos interiores de triángulos y cuadriláteros.
¿Qué vamos a aprender?
Trabajarás con el aprendizaje esperado “Analiza la existencia y unicidad en la construcción de triángulos y cuadriláteros, y determina y usa criterios de congruencia de triángulos”.
Te sugiero que tomes una posición que sea adecuada y cómoda para realizar las actividades que se presentaran a continuación. No te distraigas, pon mucha atención.
Para lograr un mejor desempeño en tus actividades, te recomiendo tener siempre cerca de ti:
- Tu cuaderno, o bien, hojas reutilizables
- Lápiz
- Goma
- Regla
- Y tú libro de texto de la asignatura de Matemáticas
Durante la sesión analizarás la relación que existe entre los ángulos que se forman entre dos rectas paralelas que son cortadas por una transversal, lo que te permitirá justificar algunas de las propiedades de los triángulos, como es la suma de la medida de sus ángulos interiores.
¿Qué hacemos?
Observa la siguiente situación
“En la casa de mi amiga Andrea hay un adorno en la pared que está formado por espejos, con forma de triángulos y cuadriláteros. Una parte del diseño, con forma de triángulo, se rompió y para repararlo es necesario conocer las medidas de los lados y ángulos.”
Para conocer la medida de los lados, Andrea usó una regla que tenía en casa, pero calcular la medida de los ángulos representó un reto mayor, ya que no tenía en casa un transportador, pero ella ya conocía algunas de las medidas, aunque otras no. Un dato importante que debes tomar en cuenta es que el espejo dañado se encuentra entre dos rectas paralelas.
A continuación, te presento una imagen del diseño con algunas de las medidas que tiene Andrea.
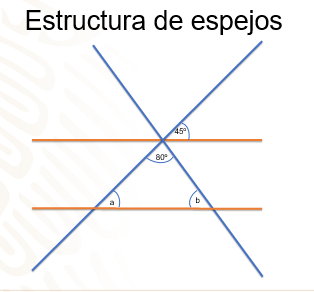
Como puedes observar, la parte del espejo que se debe conseguir tiene forma de triángulo escaleno, es decir, todos son lados son desiguales y éste se encuentra entre dos rectas paralelas, esto es fácil de comprobar ya que la distancia perpendicular entre ambas siempre es la misma. Por otro lado, Andrea ya tenía conocimiento de que uno de los ángulos del triángulo medía 80 grados y que uno de los ángulos de un espejo de la parte superior, medía 45º, como se muestra.
¿Esta información será suficiente para que Andrea pueda determinar la medida de los otros ángulos del espejo dañado?
Para que Andrea logre calcular la medida de los ángulos que faltan, debe utilizar la relación que existe entre los ángulos que se forman cuando dos rectas paralelas son cortadas por una transversal, así como el resultado de la suma de los ángulos internos de un triángulo, ¿lo recuerdas?
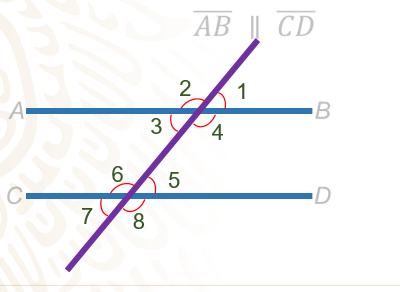
Cuando dos rectas paralelas son cortadas por una recta transversal se obtienen ocho ángulos, como puedes observar. La característica de estos ángulos es que puedes encontrar algunos pares que son iguales entre sí.

En primer lugar, se sabe que, cuando dos rectas se cortan, los ángulos opuestos por el vértice son iguales. En este caso, se tiene cuatro parejas de ángulos que son opuestos por el vértice y por lo tanto, son iguales. En este caso, con el ángulo 1 con el ángulo 3, el ángulo 2 con el 4; el 5 con el 7 y el 6 con el 8.
Ahora observa lo que sucede con los ángulos que se forman entre ambas rectas cortadas.
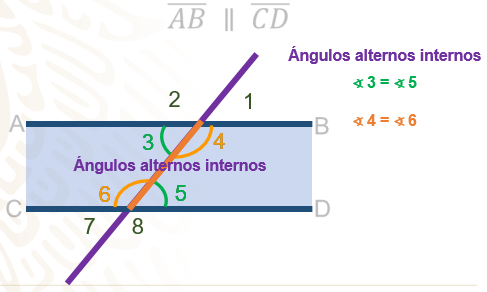
Una de las parejas de ángulos que se forman, son los ángulos alternos internos, como son los ángulos 3 y 5 y los ángulos 4 y 6 y reciben su nombre ya que se encuentran entre las paralelas y en lados opuestos de la transversal. Cada par de estos ángulos son iguales entre sí, es decir, el ángulo 4 es igual al ángulo 6 y el ángulo 3 es igual al ángulo 5.
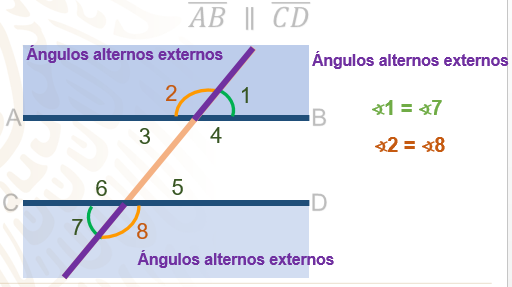
Otros pares de ángulos que cumplen con esta característica, es decir, que son iguales, son los alternos externos, que como su nombre lo indica, los puedes encontrar fuera de las paralelas, así mismo, un ángulo se encuentra de un lado de la transversal y el otro del lado opuesto, por ejemplo los ángulos 1 y 7 y los ángulos 2 y 8, son ángulos alternos externos, cuya medida es la misma, entre sí.

Los ángulos correspondientes son aquellos que se encuentran del mismo lado de las paralelas y del mismo lado de la transversal, por ejemplo, los ángulos 3 y 7; y 2 6, no pierdan de vista que los ángulos que estoy mencionando son iguales entre sí.
¿Qué otras parejas de ángulos son correspondientes?
Estos son los ángulos 1 y 5 y los ángulos 4 y 8.
Ahora piensa y dime si recuerdas la medida de la suma de los ángulos interiores de un triángulo.
La suma de los ángulos interiores de cualquier triángulo siempre será de 180º. Y existen diferentes maneras de demostrarlo, observa una de ellas

Como puedes observar, si recortas los ángulos de un triángulo y los pegas consecutivamente uno después del otro, de manera que compartan un lado, obtendrás un ángulo llano, o bien de 180 grados.
Recuerda que trabajaste con un triángulo que se encuentra entre dos rectas paralelas y para encontrar la medida de los ángulos y poder reparar el adorno, se deben hacer uso de los conocimientos que acabas de recuperar. Observa de nuevo.
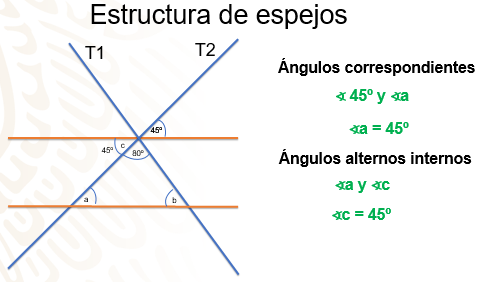
Analiza detenidamente y di qué pares de ángulos entre las paralelas ubicas y que además sirven para descubrir la medida de los ángulos internos del triángulo, es decir, de los ángulos a y b.
Es el ángulo marcado con la letra “a” y el ángulo que mide 45º son iguales entre sí, ¿recuerdas por qué? ¿Qué tipo de ángulos representan?
Muy bien, reciben el nombre de ángulos correspondientes, respecto a las paralelas y a la transversal T2, y son iguales. Por lo tanto, la medida del ángulo “a” es igual a 45 grados.
Considera el ángulo “c” que se muestra. Este ángulo “c” es alterno interno del ángulo a, con respecto a las paralelas y la recta T1, por lo tanto, el ángulo c mide 45º.
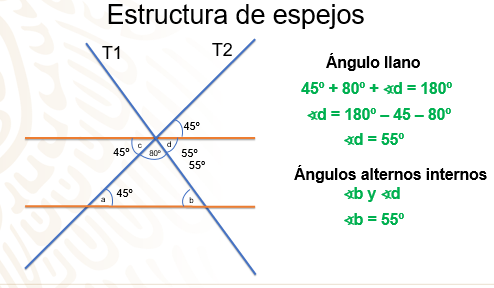
Ahora, considera el ángulo “d” que, con el ángulo “c” que mide 45º y con el ángulo de 180º forman un ángulo llano, es decir, de 180º. Para conocer su medida, a 180º le restas 45º y 80º, obteniendo 55º, es decir, el ángulo “d” mide 55º.
Si observas las rectas paralelas y la transversal T1, los ángulos “b” y “d” son alternos internos, por lo que son iguales. Así se puede justificar que el ángulo “b” mide 55º.
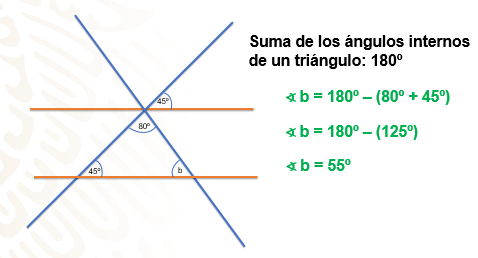
Otra forma de conocer la medida del ángulo “b”, únicamente debes calcular la diferencia entre los 180 grados y las medidas que ya se tienen, es decir, sumar los 80 grados más los 45, lo que da como resultado 125 grados. Con esto, ya puedes sacar la diferencia para saber cuál es la medida del ángulo “b”, de esta manera se tiene que 180 grados menos 125 es igual a 55 grados. La medida del ángulo “b” es igual a 55 grados.
Comprueba que el resultado es correcto, para eso sumarás las medidas de los ángulos interiores del triángulo.

80 grados más 45 grados, más 55 grados es igual a 180º. Así se confirma que el resultado es correcto.
Ahora, con la medida de los lados y de los ángulos del espejo roto con forma de triángulo, Andrea ya puede dirigirse a algún establecimiento para comprar el espejo y así, poder reparar su adorno.
Ahora, aplicando lo visto sobre la medida de los ángulos interiores de los triángulos, trabaja con un esquema similar.
Analiza detenidamente la información e intenta encontrar la manera de calcular la medida de los ángulos internos del triángulo que se muestra.

En esta ocasión puedes observar que las medidas de los ángulos interiores del triángulo están señaladas con expresiones algebraicas, es decir, un ángulo está señalado con la expresión 2x-8, otro con la expresión x+8 y ¿qué más observas?
En uno de los ángulos internos no está señalada con una expresión algebraica, pero a partir de lo que observas, ¿puedes descifrar la expresión que representa la medida de ese ángulo?
Efectivamente, puedes hacer uso de la relación entre los ángulos que se forman entre las paralelas cortadas por una transversal, en este caso, el ángulo que mide 6x es alterno interno, del ángulo del triángulo, cuya medida falta, entonces, dicho ángulo mide también 6x.
Ya que tienes las 3 expresiones que representan a cada uno de los ángulos internos, ¿cómo puedes calcular las medidas?
Sabiendo que la suma de los ángulos interiores de un triángulo es 180º, se puede establecer una ecuación para encontrar las medidas.

Es necesario sumar las expresiones e igualarlas con 180 grados, que es la suma de los ángulos internos del triángulo. La ecuación es: (2x – 8) + (x + 8) + (6x) = 180.
En este caso, se usan los paréntesis para diferenciar cada uno de los ángulos y puedes eliminarlos ya que no afectan a la ecuación, en seguida, puedes simplificar agrupando los términos que son semejantes, 2x + x + 6x, lo que da como resultado 9x, así se tiene 9x – 8 + 8 = 180 grados.
Continúa resolviendo, 8 que está restando con 8 que está sumando es igual a cero, por lo tanto, la ecuación simplificada queda como 9x = 180 grados.
Ahora, ¿qué tienes que hacer para resolver la ecuación?
Para resolver la ecuación, se hace uso de las propiedades de la igualdad, es decir, para despejar equis y conocer su valor, se dividen ambos miembros de la ecuación entre nueve, por lo tanto, se tiene en el primer miembro de la ecuación 9x/ 9 y en el segundo 180/9. Resuelve 9x/9, que es igual a 1x, recuerda que pueden no escribir el número uno y; eso es igual a 180/ 9 de lo que resulta 20 grados, es decir, x = 20 grados.
Como pudiste ver, el problema anterior es un ejemplo claro de cómo temas claves de esta asignatura se involucran en la resolución de este tipo de situaciones, en este caso fueron tres los temas.
Ya tienes el valor de la literal que involucrada en las expresiones algebraicas que representan la medida de los ángulos internos del triángulo, pero aún falta calcular dicha medida. ¿Cómo puedes hacerlo?
Para saber la medida de los ángulos, debes sustituir a la literal en cada una de las expresiones algebraicas por su valor numérico y resolver las operaciones.
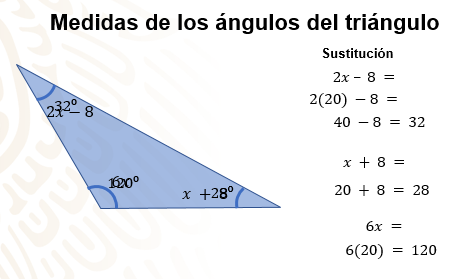
Aquí te presento la sustitución del valor de la literal. Comienza con la expresión 2x – 8, la cual queda como 2(20) – 8. Así se tiene que 2(20) = 40 y 40 – 8 = 32, ya tienes la medida del primer ángulo, 32 grados; la siguiente expresión es x + 8, es decir, 20 + 8, el resultado es 28 grados; y para el último ángulo, la expresión algebraica es 6 equis, así que debes multiplicar 6 (20), el resultado es 120 grados.
Para comprobar que esto es cierto sumas las tres medidas
Ya tienes la medida de cada uno de los ángulos internos del triángulo: 32, 28 y 120 grados, si sumas esas medidas obtienes los 180 grados que corresponden a la suma de los ángulos interiores del triángulo.
Trabaja con un ejemplo diferente, analiza la siguiente imagen y trata de encontrar la medida de los ángulos señalados.
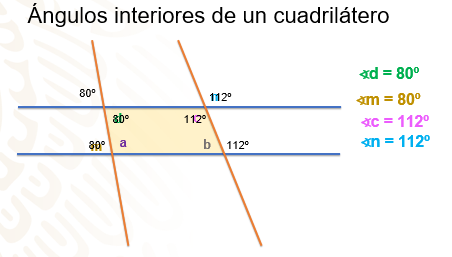
Como puedes observar, parte del reto consiste en encontrar la medida de los ángulos internos del cuadrilátero que se forma con las paralelas R1 y R2 y las dos transversales. Esto te ayudará a recordar cuál es el resultado de la suma de estos ángulos en un cuadrilátero.
Comienza identificando los ángulos que son iguales, recuperando los conocimientos que ya has visto durante la sesión. Como puedes ver, el ángulo señalado con la letra “d” es opuesto por el vértice con el ángulo que mide 80 grados, por lo tanto, también mide 80 grados; continuemos, el ángulo “m” también mide 80 grados por ser correspondientes al ángulo de 80 grados.
A partir de los datos que se muestran y los que has obtenido, ¿qué otra medida puedes encontrar?
Bien, también puedes obtener la medida del ángulo “c”, ya que es alterno interno con el ángulo que mide 112 grados y el ángulo “n” que es correspondiente con el mismo ángulo de 112 grados.
En este punto, es importante que recuerdes la característica de los ángulos suplementarios. Dos ángulos son suplementarios, si al sumarlos te da como resultado 180 grados.
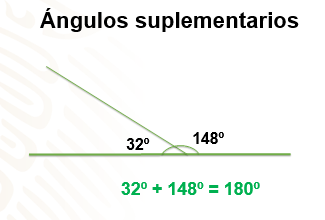
Aquí un ejemplo, si sumas la medida de los ángulos 32 más 148, da como resultado 180 grados, puedes comprobarlo en tu cuaderno trazando algunos los ángulos.
Con esta información, ya puedes encontrar la medida de los ángulos faltantes.
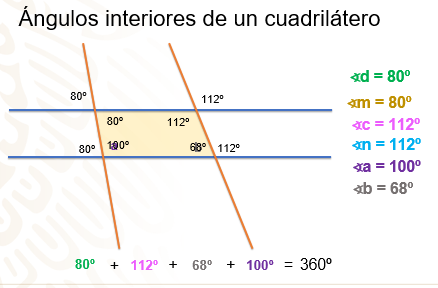
El ángulo “a” y el ángulo “m” son ángulos suplementarios, ya que juntos forman un ángulo de 180 grados; si la medida del ángulo “m” es 80 grados, ¿cuál es la medida del ángulo “a”?
El ángulo “a” mide 180 – 80 = 100 grados. Ahora, ¿cuál es la medida del ángulo “b”?
El ángulo “b” mide 68 grados por ser suplementario del ángulo “n”, que mide 112 grados.
Y ¿qué resultado se obtiene al sumar los ángulos internos del cuadrilátero que se forma con las paralelas y transversales? Observa, 80 + 112 + 68 + 100, da como resultado 360 grados.
Este número corresponde a la suma de los ángulos internos de cualquier cuadrilátero.
Observa el siguiente ejemplo para justificar lo anterior.

Si trazas una diagonal el cuadrilátero queda dividido en dos triángulos, llamarás a sus ángulos a, b, c y d, e, f, respectivamente. Como sabes a + b + c = 180º y d + e + f, también es igual a 180º. Por lo que puedes afirmar que la suma de los ángulos de cuadrilátero es de 360º.
Trabaja con otro cuadrilátero, haz uso de los conocimientos que ya has trabajado para encontrar la medida de los ángulos marcados con una literal. Analiza la imagen que se presenta a continuación e identifica por cuál de los ángulos puedes empezar, tienes diferentes opciones.

¿Cómo puedes obtener la medida de los ángulos del cuadrilátero?
Primero tienes que tomar nota de la medida del ángulo marcado con la literal equis, ya que es opuesto por el vértice con el ángulo de 95 grados, por lo tanto, también mide 95 grados.
Así solo queda una sola literal, y obtienes la ecuación y + (y +17) + 95 +( y + 44), es igual a 360, agrupando los términos semejantes queda: 3y + 156 = 360, para eliminar el número 156, debes restar esa cantidad en ambos miembros de la igualdad, por lo que anotas 3y + 156 – 156 = 360 – 156, resuelves las operaciones y tienes que 3y es igual a 204; ahora simplificas el coeficiente 3, para ello, divides entre 3 ambos miembros, al resolver tienes “y” es igual a 68.
Ya que cuentas con este valor, no tienes más que sustituirlo en cada una de las expresiones algebraicas y resolver las operaciones.
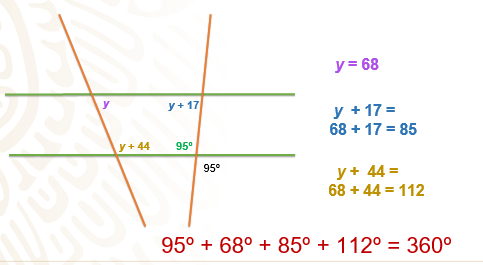
El valor y = 68; en la segunda expresión tienes y + 17, tenemos 68 + 17 = 85; por último, la expresión es y + 44, sustituyendo y, queda como 68 + 44 = 112 y si sumas las 4 cantidades que ya tienes, confirmas que la suma de los ángulos será de 360º.
El reto de hoy:
Según algunas investigaciones, los vitrales comenzaron a crearse por artesanos desde varios años antes de esta era, el material que se utiliza es vidrio y generalmente puedes apreciarlos en construcciones antiguas, casi siempre están elaborados con una mezcla de diferentes colores y formas.
A continuación, a manera de reto analiza la siguiente situación.
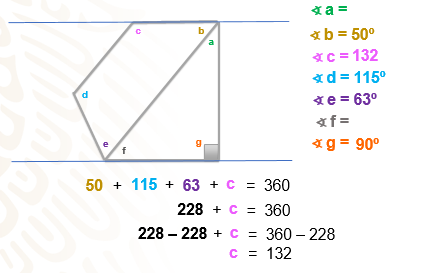
Como puedes ver, el diseño es un pentágono irregular, y dos de sus lados son paralelos, identifica que, si trazas esta diagonal, se forma un triángulo rectángulo, por lo tanto, se sabe que el ángulo g mide 90º.
¿Qué otra figura observas? Bien, puedes ver un cuadrilátero. Las medidas con las que ya se cuenta son: ángulo “b” igual a 50 grados, ángulo “d” igual a 115 grados y ángulo “e” igual a 63 grados.
¿Con esta información ya puedes obtener las medidas de los otros ángulos?
Comienza por calcular la medida del ángulo “c”. Sólo debemos plantear la ecuación en la que representarás la suma de los 3 ángulos que ya tienes más el ángulo “c” igualada a 360. La ecuación es: 50, más 115, más 63, más c es igual a 360; sumas las cantidades y la igualdad queda 228 + c = 360. Ahora, aplica las propiedades de la igualdad para eliminar el 228 en el primer miembro de la igualdad, restas 228 en ambos lados de la ecuación; así tienes que 228 – 228 + c = 360 – 228; resuelve las operaciones y así encuentras que la medida del ángulo c es igual a 132 grados.
Ahora, únicamente falta encontrar la medida del ángulo a y el ángulo f.
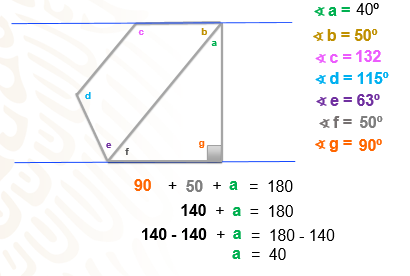
Analiza nuevamente, si consideras que las rectas de color azul son rectas paralelas, entonces tienes que la medida del ángulo “f” es igual a la medida del ángulo “b” -que ya son ángulos alternos internos-, por lo tanto, el ángulo “f” también mide 50 grados.
Ya sólo queda encontrar la medida del ángulo “a”.
Suma 90 + 50 + a = 180, ya que este número es el que resulta al sumar los ángulos interiores del triángulo; sumas 90 + 50, lo que da como resultado 140, así que la ecuación queda 140 + a = 180; eliminas el 140 aplicando las propiedades de la igualdad, para eso restas esta cantidad en ambos miembros de la igualdad, resuelve las operaciones resultantes y finalmente llegas a que el valor del ángulo “a” es igual a 40 grados.
Se sigue comprobando que las matemáticas se encuentran a tu alrededor, te invito a que pienses en una situación similar a las que se presentó en esta sesión, en la que identifiques ángulos entre paralelas, por ejemplo, es las protecciones de una ventana o una puerta, o bien algunos diseños en pinturas o cuadros; también pueden identificar algunos triángulos y cuadriláteros e intentar calcular la medida de sus ángulos internos, tomando como base la suma de los mismos.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas