Sucesiones aritméticas en distintos contextos

Sucesiones aritméticas en distintos contextos

Aprendizaje Esperado: formula expresiones algebraicas de primer grado a partir de sucesiones y las utiliza para analizar propiedades de la sucesión que representan.

Énfasis: resolver problemas en situaciones que representan sucesiones aritméticas: la regla, los términos faltantes y determinar si un número pertenece a la sucesión.

¿Qué vamos a aprender?

En esta sesión resolverás problemas en situaciones que representan sucesiones aritméticas, establecerás la regla que las representa, calcularás términos faltantes y determinarás si un número pertenece a la sucesión.

Para esta sesión necesitarás tu cuaderno o papel para tomar notas, así como tu lápiz, goma y sacapuntas. Si tienes una discapacidad visual prepara tus hojas leyer, punzón y regleta.

¿Qué hacemos?

Para conocer más sobre las sucesiones es necesario que se establezcan algunos conceptos importantes.

En la escuela, cuando se tiene un conjunto de nombres de un grupo y se ordenan alfabéticamente, se genera una lista o serie ordenada en la que los nombres siguen el mismo orden que las letras del alfabeto.

Esta es una sucesión de palabras, pues ordena de forma específica nombres; pero también existen sucesiones numéricas.

En esta sucesión numérica el ordenamiento de los números pertenecientes a este conjunto es de menor a mayor en orden de magnitud.

En la primera posición de la sucesión se mencionó al 1, en la segunda posición de la sucesión está el 2, que es una unidad mayor que el primer número y se podría continuar así sucesivamente.

Cuando se dice “sucesivamente” se hace referencia al criterio de ordenamiento de forma continua de igual manera para toda la lista, conjunto o, mejor dicho, sucesión de números.

Una sucesión aritmética es aquella en la que la diferencia entre términos consecutivos es la misma, es decir, constante.

Los términos de una sucesión aritmética pueden ser representados mediante una regla matemática. Esta regla puede estar representada por una expresión. Analiza el siguiente ejemplo.

En la sucesión 2, 4, 6, 8, 10, 12… es posible observar que el primer término es 2 y que el segundo término es 4. La diferencia que existe entre el 4 y el 2 es igual a 2. Nota que es la misma diferencia que existe entre cada término y su antecesor, la diferencia entre 6 y 4 es 2, la diferencia entre 8 y 6 también es 2. En esta sucesión, como la diferencia es constante, representa una sucesión aritmética.

Como te puedes dar cuenta, para encontrar algún término de esa sucesión, sólo es necesario multiplicar por 2 a la posición del término que se busca. Por ejemplo, para el término 2, se multiplica 2 por la diferencia, 2 y esto es igual a 4. Si se busca el décimo término de la sucesión, debes multiplicar 10 por 2; lo que resulta 20.

¿Puedes comprobar que esta observación es correcta?

Para comprobarlo, se puede mencionar que, a cada término, se le asocia una posición “n”; esto significa que la “n” tomará el valor correspondiente al número del término en cuestión. Cabe señalar que “n” siempre será un número natural; es decir, los que se usan para contar.

Generalmente cada término se representa con la letra “a”, acompañada del número de término en subíndice. Por ejemplo, “a1” representa al primer término. Para este caso “a1” es igual a 2. Como ya se había mencionado, la diferencia es de dos; es decir, a cada término se le van sumando dos unidades más; de esta manera se puede continuar con la sucesión, dos más 2, cuatro, más 2, seis, más 2, ocho, más 2, diez, más 2, doce, más 2 catorce, más 2, dieciséis, más 2, dieciocho, más 2, veinte. Así que, el término que ocupa la décima posición es 20; es decir, que la observación es correcta.

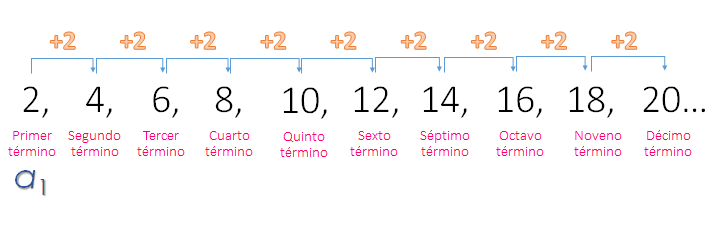
Como ves, es muy tardado estar pensando en cada término de la sucesión de esta manera.

Entonces, ¿cuál es la forma de encontrar un término más rápido?

Escribe en tu cuaderno la respuesta; ya que más adelante podrás verificar si respondiste correctamente.

Para encontrar más rápido cualquier término de la sucesión, es de utilidad conocer el término general de ella.

La expresión general de una sucesión aritmética es de la forma “an” es igual a “d” por el binomio “n” menos 1 más “a1”; donde “an” representa al enésimo término de la sucesión, “n” representa el número de la posición del término, “d” es la diferencia entre dos términos consecutivos y “a1” es el primer término de la sucesión.

En el caso de la sucesión que se está analizando, como la diferencia es 2 y el primer término también es 2, sustituyes estos valores en la expresión general y obtienes que, “an” es igual a 2 por “n” menos 1 más 2.

Realiza las operaciones para simplificar la expresión, aplica la propiedad distributiva, dos por la diferencia de “n”, menos uno y así obtienes “an” = 2n -2 +2.

Al simplificar al sustraendo 2 con el sumando 2, queda cero; por lo tanto, queda la expresión algebraica “an” = 2n, que representa regla de la sucesión.

Para hacer la comprobación, encontrarás el décimo término. Si sustituyes el valor de n =10 en la expresión algebraica a10 = 2n obtienes: a10 = 2(10); y al realizar la operación, dos por diez es igual a 20. Por lo tanto, a10 = 20.

Ya viste que se comprobó que es correcta la operación. Ahora, ya puedes encontrar más términos, sin necesidad de ir uno por uno.

Se te invita a utilizar la regla de la sucesión para encontrar los términos 60, 150 y 500. Puedes compartir tus resultados con tu maestra o maestro, para recibir retroalimentación al respecto.

Quizás te pueda resultar sencillo, ya que al conocer la expresión general que solo te indica multiplicar el lugar por 2, puedes hacer los cálculos de manera mental, así puedes afirmar que para el término 60, le corresponde el número 120, al 150, el número 300, y para el término 500, el número es 1000.

Se espera que hayas coincidido con estos resultados, en tu ejercicio. Ahora, revisarás un pequeño resumen de lo que se explicó anteriormente, presta atención y no olvides tomar nota de la explicación.

Una sucesión numérica se representa como una lista de la forma, “1, 2, 3, 4…”. A cada número se le llama término de la sucesión y los tres puntos indican que la sucesión continúa indefinidamente.

A las sucesiones en las cuales la diferencia entre dos términos consecutivos es constante, se les llama sucesiones con progresión aritmética. Para obtener cualquier término de una sucesión, es conveniente representar la regla de la misma con una expresión algebraica. A esta expresión se le conoce como regla general y es de la forma “an” igual a “d” por “n” menos 1 más “a”, donde “n” representa el número de término, “d” es la diferencia entre dos términos consecutivos y “a1” es el primer término de la sucesión.

Con toda la información recibida, resuelve lo siguiente.

Carmen quiere abrir un refugio para perros; por eso les construirá casas, una junto a la otra para alojar a los caninos. De inicio quiere construir 35 casitas.

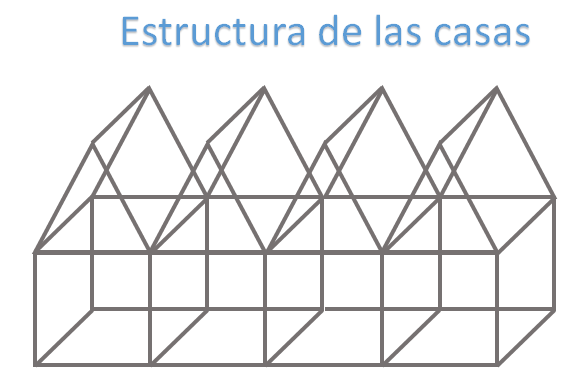
La estructura de las casas será de varillas del mismo tamaño y el diseño consiste en juntar la estructura de cada casa con la estructura de la anterior; como puedes observar, el número de varillas que necesita para construir la siguiente casa es la misma.

De la forma en que lo plantea, ahorraría muchas varillas y, eventualmente, podría alojar a más perros. ¿Qué te parece si se le ayuda a calcular cuántas varillas se necesitan para 35 casas?

Pero antes, hay que analizar los datos que brinda el problema y que son necesarios para obtener la sucesión. ¿Cuáles son los datos que crees que se necesitan?

Pensando en la regla general de las sucesiones, se necesita saber cuántas varillas ocupará la primera casita, es decir, cuál es el primer término de la sucesión y cuál es la diferencia entre los números de la sucesión.

Para obtener los datos que se mencionan, primero se tiene que pensar en las varillas que se necesitan.

Para la primera casa se ocuparon 17 varillas; por lo tanto, el primer término de la sucesión es 17. Para la segunda casa se ocuparon 13 varillas; por lo tanto, el segundo término de la sucesión es 30. Para la tercera casa se ocuparon otras 13 varillas; con lo cual, el tercer término de la sucesión es 47. Puedes notar que la diferencia entre dos números consecutivos es 13; con esto, se puede afirmar que el siguiente número será 56, el siguiente 69, etcétera.

Se puede afirmar entonces, que el primer término de la sucesión, es 17; por lo tanto, al representar algebraicamente la sucesión, se tiene que “a1” es igual a 17 y que la diferencia, “d” es igual a 13.

Con estos datos ya puedes establecer la regla de la sucesión que se genera con el número de varillas “an” = “d” por “n” menos 1 más “a”. Sustituye 13, que es la diferencia, y 17, que es el primer término de la sucesión; así se obtiene an = 13 por “n” menos 1 más 17. Realiza la operación indicada; es decir, trece por “n”, menos uno y obtienes: 13 “n” menos 13 más 17.

Al simplificar, el sustraendo 13 más 17 positivo, obtienes 4 positivo; por lo tanto, la expresión quedaría 13 “n” más 4. Con esto se puede ver que las expresiones 13 “n” menos 13 más 17 y 13 “n” más 4, son equivalentes y ambas permiten obtener cualquier término de la sucesión.

Ya que conoces la expresión que representa esta situación y sabes que el número de casas que desea construir Carmen es de 35, el término de la sucesión que tienes que encontrar está determinado por este número; es decir, “n” es igual a 35.

Ahora, sólo debes sustituir este valor en la expresión 13 “n” más 4, quedando 13 por 35, más 4, que es igual a 455, más 4, y finalmente obtienes 459; por lo tanto, Carmen necesitará 459 varillas para construir 35 casas.

Se entiende entonces que si Carmen quiere saber la cantidad de varillas para cualquier número de casas sólo debe multiplicar ese número por 13 y sumarle cuatro.

Es importante saberlo, ya que quizá en algún otro momento, requiera construir más casas y para ello saber cuántas varillas necesitará. Por ejemplo, para construir 15, 45 o 100 casas, ¿cuántas varillas necesitaría en cada caso?

Para construir 15 casas se debe multiplicar 13 por 15 más cuatro, que son 195 más cuatro, que son 199. Para 45 casas, se multiplica 13 por 45 más cuatro; o sea, 585 más 4, igual a 589. Y para 100 casas, 13 por 100, más cuatro, es mil trescientos más 4, que son mil trescientos cuatro. Por lo tanto, Carmen requiere de 199, 589 y 1304 varillas, respectivamente

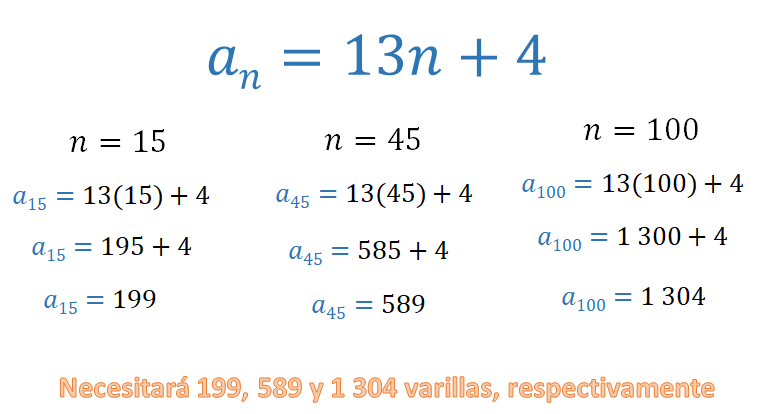
Si Carmen sólo consigue 394 varillas, ¿cuántas casas podrá construir?

Como 394 es el total de varillas, este número debe ser el resultado de las operaciones; entonces hay que hacer las operaciones contrarias.

Para esto se puede plantear una ecuación de primer grado, en la expresión general “an” = 12n + 4, se sustituye a “an” por 394 y se obtiene la ecuación, 13n + 4 = 394.

Ahora solo tienes que resolver la ecuación. Entonces restas 4 en ambos miembros de la igualdad, obteniendo la ecuación 13n = 390, y para despejar a “n”, divides ambos lados entre 13, obteniendo que n = 30. Por lo tanto, se pueden construir 30 casas.

¿Y qué dices de 480 varillas?

Trata de hacerlo mentalmente, 480 menos 4 son 476, entre 13 son 36.61, Pero, como ves no puede haber 36.6 casas.

Así es, los cálculos son correctos. Cuando se obtiene un número decimal, quiere decir que no se encuentra dicho número en la sucesión; en este caso, el 480 no pertenece a la sucesión.

Ya se había mencionado que “n”; es decir, el lugar de la sucesión, siempre debe ser un número natural. Si recuerdas a veces, también se revisan este tipo de problemas, pero con figuras.

Así es, generalmente las sucesiones se presentan como una serie de números o como una secuencia de figuras; pero si ya lo pudiste resolver con un problema, ten por seguro que con figuras también podrás hacerlo. Presta atención a lo siguiente.

Observa la siguiente sucesión hecha con octágonos regulares. Si analizas el perímetro de las figuras se genera una sucesión aritmética.

¿Puedes identificarla? ¿Podrías establecer la regla de la sucesión?

En este caso la pregunta es ¿qué número de figura tendrá un perímetro de 35 unidades? Escribe tu respuesta en tu cuaderno, primero busca la regla de la sucesión.

Antes de calcular la regla de la sucesión, debes encontrar el primer término y la diferencia entre dos términos consecutivos. ¿Puedes realizarlo?

Primero se completará la tabla con el perímetro de las tres primeras figuras. La primera figura tiene un perímetro de 8 unidades; por lo tanto, 8 es el primer término de la sucesión. La segunda figura tiene 14 unidades de perímetro, es decir, 14 es el segundo término de la sucesión, y la tercera figura, tiene 20 unidades de perímetro. Con esto se puede notar que la diferencia entre términos consecutivos es 6.

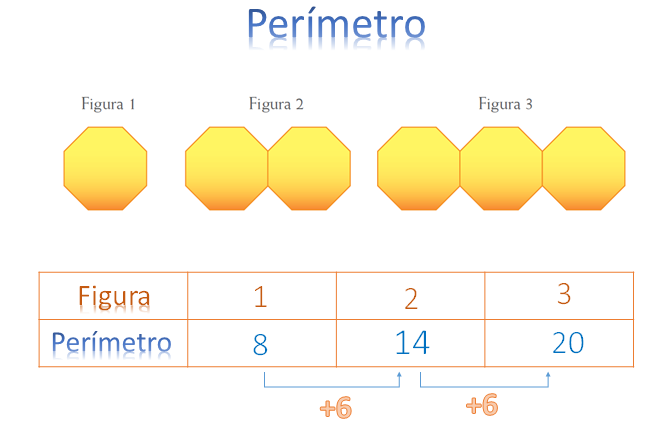
Como la diferencia es 6, se puede afirmar que se trata de una sucesión aritmética y, siguiendo ese patrón, los siguientes números en la secuencia son, 26, 32, 38, etcétera.

¿Qué puedes observar en esta sucesión?

No existe ninguna figura, en esta sucesión, que tenga un perímetro de 35 unidades.

Pero hay que comprobarlo. Primero, para obtener la regla de esta sucesión, debes saber que el primer término es 8; por lo tanto, “a1” es igual a 8 y que la diferencia es 6; por lo que “d” es igual a 6.

La regla de la sucesión es an = “d” por “n” menos 1 más “a1”. Sustituye 6, que es la diferencia y 8, que es el primer término de la sucesión; así obtienes 6 por el binomio “n” menos 1, más 8. Realiza las operaciones indicadas para simplificar la expresión y obtienes 6 por “n” menos uno y se tiene 6“n” menos 6 más 8. Al simplificar queda la expresión an = 6 “n” más 2.

Ahora usa tus conocimientos algebraicos, para comprobar que 35 no pertenece a la sucesión.

Sustituye a “an” por 35 en la expresión general y obtienes la ecuación 6“n” más 2, igual a 35.

6“n” más 2 menos 2, igual a 35 menos 2.

6“n”, igual a33.

6“n” entre 6, igual a 33 entre 6.

“n” igual a 5.5.

Al obtener un número decimal, puedes comprobar que el número 35 no pertenece a la sucesión; por lo tanto, ninguna figura de esta sucesión tiene 35 unidades de perímetro.

Entonces la expresión de una sucesión tiene dos funciones, si se usa como una expresión algebraica, puede encontrar cualquier término de una sucesión; pero si se usa como una ecuación, es decir, igualándola a una cantidad, se puede saber si dicha cantidad pertenece o no a la sucesión.

Ahora hay que resolver un último ejemplo. Lee con atención.

El primer término de la sucesión es 4 y la diferencia entre dos términos consecutivos es tres. ¿Puedes decir los primeros cinco términos de la sucesión? Escribe la sucesión que se genera en tu cuaderno y verifica tus resultados.

El primer término es cuatro y la diferencia es tres; entonces quedaría 4 más 3, 7, más 3, 10, más 3, 13, más 3, 16, etcétera.

Ahora, hay que calcular la expresión algebraica para esta sucesión, sabiendo que 4 es el primer término y 3 la diferencia.

En la expresión an = “d” por “n” menos 1 más “a”, sustituye 3, que es la diferencia y 4, que es el primer término de la sucesión; así se obtiene 3 por el binomio “n” menos 1 más 4. Realiza la operación indicada, es decir, 3 por “n” menos uno y obtienes 3 “n” menos 3, más 4. Al simplificar el sustraendo 3 con el sumando 4, obtienes 1 positivo; por lo tanto, la expresión quedaría an = 3 “n” más 1.

Utilizando esta expresión, ¿podrías calcular qué números aparecerán en los lugares 10, 16 y 50?

Para “n” igual a 10, 3 por 10 más uno, 30, más uno, igual a 31.

Para “n” igual a 16, 3 por 16 más uno, 48 más uno, igual a 49.

Para “n” igual a 50, 3 por 50 más uno, 150 más uno, igual a 151.

En el lugar 10 se encontrará el número 31, en el lugar 16 el 49 y en el lugar 50 el 151.

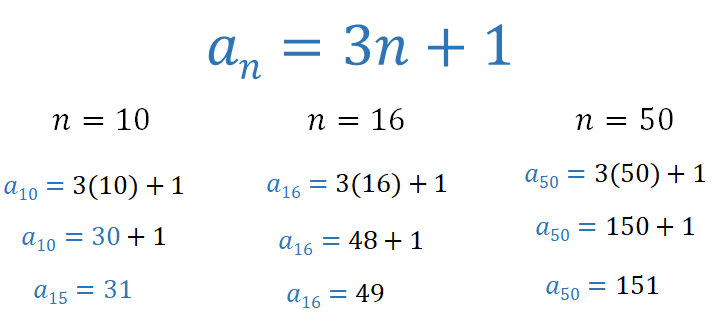
Ahora necesitas saber en qué lugar de la secuencia se encontrarán los números 70, 154 y 300. Puedes hacerlo mentalmente, haciendo las operaciones contrarias y utilizando ecuaciones.

3 “n” más 1, igual a 70.

3 “n” más 1 menos 1, igual a 70 menos 1.

3 “n” igual a 69.

3 “n” entre 3, igual a 69 entre 3.

“n” igual a 23.

Como 23 es un número entero, quiere decir que el número 70 aparecerá en el lugar 23.

3 “n” más 1, igual a 154.

3 “n” más 1, menos 1, igual a 154 menos 1.

3 “n” igual a 153.

3 “n” entre 3, igual a 153 entre 3.

“n” igual a 51.

Como 51 es un número entero, quiere decir que el número 154 aparecerá en el lugar 51.

3 “n” más 1, igual a 300.

3 “n” más 1, menos 1, igual a 300 menos 1.

3 “n” igual a 299.

3 “n” entre 3, igual a 299 entre 3.

“n” igual a 99.666…

Como 99.666… es un número decimal, quiere decir que el número 300 no pertenece a esta sucesión.

Tú en casa, ¿tuviste los mismos resultados?, se espera que sí. Si te es posible, contacta a tu maestra o maestro para compartir tus respuestas.

El reto de hoy:

Si tienes tu libro de texto de Matemáticas, ubica en él, este tema y resuelve todo lo que puedas sobre lo que revisaste el día de hoy, para que puedas profundizar más.

Concluye los ejercicios que se te solicitaron en el desarrollo de la sesión, en caso de que no los hayas terminado.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html

1