Cálculo de porcentajes I
Cálculo de porcentajes I
Aprendizaje esperado: resuelve problemas de cálculo de porcentajes, de tanto por ciento y de la cantidad base.
Énfasis: calcular la cantidad final después de agregar o quitar un porcentaje. Determinar la cantidad inicial después de aplicar un porcentaje.
¿Qué vamos a aprender?
Esta sesión tiene por aprendizaje esperado “Resuelve problemas de cálculo de porcentajes, de tanto por ciento y de la cantidad base”.
Como en cada lección se pondrán retos, en este caso es un problema, cuando se trabaja el tema de porcentajes, con la finalidad de despertar el interés por el estudio de las matemáticas.
Para lograr un mejor desempeño en las actividades, te recomiendo tener a tu disposición:
- Cuaderno, o bien, hojas reutilizables.
- Lápiz.
- Goma.
- Y tu libro de texto de la asignatura de Matemáticas de primer grado.
¿Qué hacemos?
Lee el siguiente problema.
“Una tienda vende los tenis de distintos modelos con un costo $1 500.00, por un momento parecen costosos. Pero la tienda por inauguración ofrece el 50 por ciento de descuento sobre el precio base, más el 30 por ciento de descuento adicional, más el 20 por ciento de descuento extra adicional”
Ahora analiza, 50% + 30% + 20% = 100%, ¿piensas que al comprar unos tenis serán gratis?
Al final de la sesión serás capaz de contestar con base en lo aprendido.
De esta forma cuando encuentres ofertas similares ayudarás a tus padres y/o familiares a tomar la mejor decisión al comprar.
Recuerda que “por ciento” significa “por cada cien” y se refiere a la razón entre una cantidad dada y un total de los cien elementos; también se llama “tanto por ciento” esto es, “una cantidad por cada 100”. Se utiliza el símbolo “%” para indicar un tanto por ciento, por ejemplo, 27 de cada 100 se expresa como 27/100 o 27%.
De igual manera, “uno de cinco” se expresa como 1/5, 20/100 o 20%.
Practica cómo expresar porcentajes en sus diferentes formas para familiarizarte con las distintas opciones de representación. Para ello, completa la siguiente tabla buscando en cada caso la forma de resolverlo.

Si observas, se tienen cuatro columnas; en la primera se pide una expresión sobre tanto por ciento; en la segunda escribirás la expresión como una fracción; en la tercera columna, una fracción equivalente con denominador 100 en la tercera la expresión decimal, es decir el resultado de dividir el numerador entre el denominador de la fracción, y por último, representamos el valor de la expresión decimal por cien y agregamos el símbolo de porcentaje %.
En la primera fila aparece la expresión 28 de cada 50, como fracción quedaría 28/50, pero también nos piden una fracción con denominador 100, recuerden que para tener una fracción equivalente debemos multiplicar o dividir los dos términos de la fracción por el mismo número.
En este caso observa que para pasar el denominador de 50 a 100 basta con multiplicar por dos, por lo tanto, multiplicas numerador y denominador por dos y nos queda 56/100.
Para la expresión decimal habrá que dividir cincuenta y seis entre 100 y basta con colocar antes del 56 un punto decimal, quedando 0.56 lo que significa cero enteros cincuenta y seis centésimos, para finalizar recuerda usar el símbolo “de porcentaje” y tomando el valor de la expresión decimal multiplicada por 100 se tiene 56%. De esta forma has completado la primera fila de la tabla.
Observa la fila dos, si observas, en la cuarta columna se tiene un valor clave para comenzar con el llenado de las demás, es decir, cero enteros siete centésimos, para llenar las columnas haremos lo contrario que en el caso anterior, en lugar de dividir debemos multiplicar el dato de la expresión decimal por 100 y obtendrás la fracción con denominador 100, siendo ésta (0.07) (100) = 7 y colocas el 100 como denominador es decir 7/100.
¿Qué pondrías en la primera y segunda columna?
Como la fracción 7/100 es irreducible, entonces en la segunda columna repetimos la misma fracción y en la primera columna queda la expresión ¡7 de cada 100!
Para la cuarta columna tomamos el valor de la expresión decimal multiplicado por cien obteniendo 7%.
Resuelve la tercera fila, la cual dice 28 de cada doscientos en la primera columna, es decir, como fracción es 28/200 para tener una fracción equivalente con denominador 100, debemos dividir entre dos, por lo tanto, haz lo mismo con el numerador y te quedará 14/100 y lo colocas en la tercera columna; con estos datos realizas la división de catorce entre cien, quedando la expresión decimal cero enteros catorce centésimos. Para concluir toma el valor de la expresión decimal multiplicada por cien y agrega el símbolo de porcentaje, quedando 14%.
¿Ya sabes qué valores van en la cuarta fila?
Si has comprendido la forma de llenar dicha tabla por favor completa la cuarta fila.
Compara tus resultados con los mostrados en la pantalla en este momento.
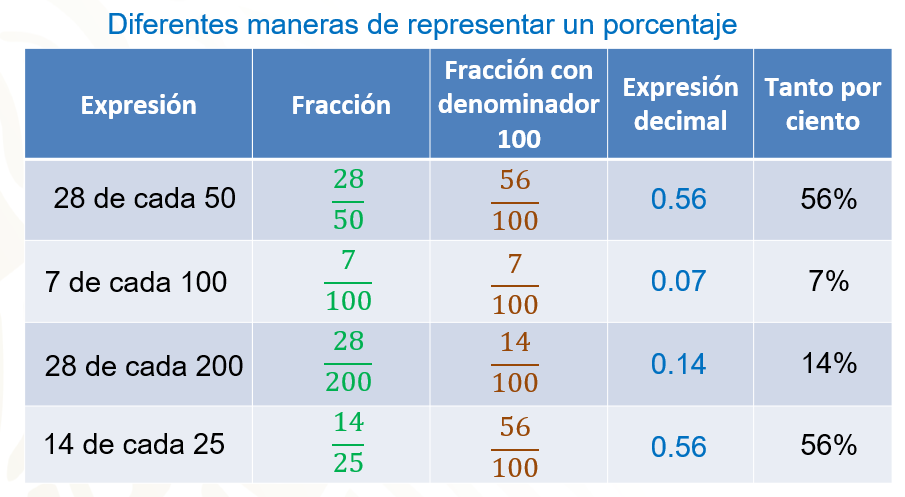
Ya has visto las distintas maneras de representar un porcentaje. Pero existen diferentes maneras o situaciones en las que se tiene que calcular un porcentaje. Por ejemplo, calcular el porcentaje que aumenta o disminuye una cantidad, conocer la cantidad final al aplicar cierto porcentaje de descuento, calcular que porcentaje representa una cantidad de otra, entre otras situaciones.
Para calcular la cantidad final que se obtiene al aplicar un porcentaje a una cantidad base o cantidad inicial, se puede proceder como sigue.
Se obtiene la cantidad que corresponde al porcentaje por aplicar. El porcentaje dado (x) se divide entre 100 y el cociente obtenido se multiplica por la cantidad base. Es decir, “y” es igual a x/100 por la cantidad base o inicial.
Para la cantidad final se suma o se resta a la cantidad base o inicial el valor de la cantidad a la que corresponde el porcentaje, es decir, cantidad base más o menos “y”.
Por ejemplo, al descontar 19 por ciento a 120, la cantidad base o inicial es 120 y el porcentaje 19%, entonces se divide diecinueve entre cien por ciento veinte, que es igual a 0.19 por 120, que es igual a veintidós punto ocho, que es la cantidad a descontar.
Por tanto, la cantidad final es igual a 120 menos 22.8 que es igual a 97.2.
Otro procedimiento consiste en restar a 100% el 19%, el resultado de la resta corresponde al porcentaje que representa la cantidad final.
Así, calcular 81% de la cantidad base, ochenta y uno entre cien por ciento veinte es igual a 0.81 por 120, que es igual a 97.2.
Con la situación anterior, viste dos maneras distintas de calcular la cantidad final cuando se aplica un porcentaje a una cantidad base.
Ahora observa la siguiente situación.
El IVA (Impuesto al Valor Agregado), es un impuesto que se aplica en muchos países y corresponde a un porcentaje de aumento que grava ciertos productos y servicios.
De acuerdo con los datos de la Procuraduría Federal del Consumidor (Profeco), el precio promedio de un refrigerador sin IVA en la Ciudad de México es de $5 031.60, que en la mayor parte de nuestro territorio nacional el IVA de un producto es del 16%.

En la tabla se muestran los porcentajes de IVA que se aplica en algunos países. En Grecia es del 23%; en Paraguay, 10%; en Puerto Rico, 11.5% y en Uruguay, 22%.
Te pregunto, ¿cuál será el precio con IVA del refrigerador si en México se aplicara el IVA que en los cuatro países de la tabla? ¿Cuál será el costo en México del refrigerador con IVA incluido?
Calcula las respuestas correspondientes a la primera pregunta, recuerda que el precio promedio del refrigerador es de $5 031.60, sin IVA, es decir, este será el cien por ciento.
Para el caso de Grecia, calcula el veintitrés por ciento de IVA a dicha cantidad que deberás agregar al precio del refrigerador, es decir, a la cantidad base.
Siguiendo el procedimiento antes mencionado, se divide veintitrés entre cien y el resultado se multiplica por $5 031.60 obteniendo $1 157.26 que será la cantidad por agregar al costo original, es decir $5 031.60 + $1 157.26 = $6 188.86. Coloca el valor en donde corresponde.
Calcula cuál sería el precio en Paraguay, siguiendo el mismo procedimiento divide diez entre cien y el resultado se multiplica por $5 031.6 dando como resultado $503.16 lo cual se suma al costo original, obteniendo $5 031.60 + $503.16 = $5 534.76.
Aprovechando el cálculo anterior, observa que cuando obtienes el 10 por ciento de una cantidad, solamente se recorre el punto decimal una posición a la izquierda. Es exactamente lo mismo que pasa cuando dividimos entre 100 y se obtiene el 1 por ciento de dicha cantidad, el punto se recorrerá dos posiciones a la izquierda quedando también los mismos dígitos.
Retomando el problema, calcula el caso de Puerto Rico. Usando el mismo procedimiento, divide 11.5 entre 100 obteniendo 0.115, multiplica dicho valor por $5,031.60 el resultado obtenido es igual a $578.63 y se agregará a la cantidad original como sigue $5 031.60 + $578.63 = $5 610.23.
Falta calcular el caso de Uruguay, comienza por dividir veintidós entre 100, obteniendo 0.22 y después multiplica el resultado por $5,013.60 que es igual a $1 106.95, dicha cantidad se agregará a la cantidad original de la siguiente manera $5 031.60 + 1 106.95 = $6 138.55.
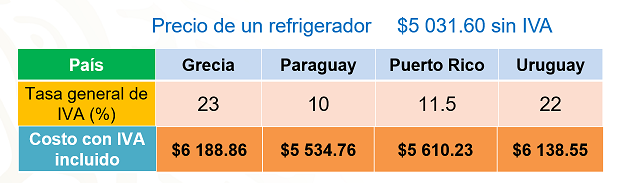
Con este dato se concluye el llenado de la tabla.
Ahora calcula cuál sería el precio aplicando el 16% de IVA en México. Ya has usado el procedimiento varias veces, te invito a seguir paso a paso el procedimiento anterior para obtener la respuesta.
Pero existe otra manera de obtener el precio final, se suma 100% que representa a la cantidad base más 16% que es el porcentaje que se aumenta, 116% se divide entre 100% y el resultado se multiplica por el precio base, es decir, 5 031.60 por 1.16 cuyo resultado es igual al precio final, 5 836.65 pesos.
Otros tres porcentajes importantes por destacar son 25%, 50% y 75 % que corresponden a 1/4, 1/2 y 3/4 respectivamente de la cantidad original. Con la práctica serás capaz de calcularlos mentalmente.
Por ejemplo, considera que el refrigerador anterior, en una tienda tiene 50% de descuento. ¿Cuál será su precio final?
Haz el cálculo de tres formas equivalentes.
Para dar respuesta, recuerda que el cincuenta por ciento equivale a un medio del valor inicial, por lo tanto, bastaría dividir ese monto entre dos o multiplicarlo por ½, que es equivalente a multiplicar por 0.5.
Primer procedimiento. Multiplica el precio final $5 836.65 por un medio, es decir, multiplicas por uno, que da exactamente el mismo valor y lo divides entre dos, obteniendo $2 918.32.
Segundo procedimiento.
Multiplica 50/100 por $5 836.65, primero multiplicas 5 836.65 por 50, dando como resultado $291 832.5; después divides entre cien, recuerda que basta con recorrer el punto decimal, dos posiciones hacia la izquierda, entonces tienes como respuesta $2 918.32 se acostumbra a dejar el resultado hasta centésimos.
Si ya conoces el factor de porcentaje del 50%, es decir el que surge de dividir uno entre dos, o cincuenta entre cien, en ambos casos nos da cero punto cinco, bastará con multiplicar $5 836.65 por 0.5 dando como resultado $2 918.32.
Es importante observar que, cuando se multiplica una cantidad por un número menor a la unidad, dicha cantidad disminuye.
Ahora analiza cómo obtener la cantidad inicial conociendo el porcentaje aplicado y la cantidad final, puedes hacerlo de la siguiente manera.
Un artículo tiene el 25% de descuento y costo final de $375.
¿Cuál era el precio inicial del producto?
Para responder, considera que se pagó el 75% de su valor real ya que el 100% menos el 25% es igual al 75%.
A partir de la proporción “cantidad base u original sobre cantidad pagada que es igual a 100% sobre porcentaje pagado”, es posible calcular cualquiera de los datos involucrados si se conocen los demás.
En ese caso se tiene costo original sobre 375 pesos que es igual a 100% sobre 50%; $375 se multiplica por 100 y el producto obtenido se divide entre 75. El resultado que se obtiene es el costo inicial. Entonces el costo original es igual a 375 por 100 que da como resultado 37 500 y lo divides entre 75. Por lo tanto, la cantidad inicial o el precio original del artículo era de $500.
Has avanzado en la solución de problemas de cálculo de porcentajes. Pon en práctica lo aprendido, resolviendo las siguientes situaciones problemáticas.
“El descuento aplicado a todos los productos de una tienda de telas es del 15%. Si Julieta compró 5 metros de tela y pagó $102 pesos, ¿cuál era el precio de la tela antes del descuento?”
En primer lugar, se sabe que hubo un decremento del costo inicial del 15%, por lo tanto 100% – 15% = 85% del valor inicial. Siguiendo el procedimiento anterior, tienes que costo base u original entre 102 es igual a 100% entre 85%. Aplicando la regla de tres directa, tienes costo original es igual a 102 por 100 y el resultado obtenido se divide entre 85. Quedando 10 200 entre 85, que da como resultado $120.
Esto quiere decir que el costo de 5 metros de tela sin descuento era de $120.
Resuelve otra situación problema.
“Al precio original de un juguete se le aplicó un 30% de descuento. Si un cliente pagó $540 por dicho juguete, ¿cuál era el costo original?”
En primer lugar, se sabe que hubo un decremento del costo inicial del 30%, por lo tanto, se pagó 100% – 30% = 70% del valor inicial. Siguiendo el procedimiento anterior, se tiene que el costo original entre 540 es igual a 100% entre 70%.
Aplicando una regla de tres directa, se tiene costo original es igual a 540 por 100 y lo que da como resultado de la multiplicación entre 70. Entonces queda 54 000 entre setenta y da como respuesta $771.42, siendo este precio el costo original del juguete.
El siguiente problema servirá como referencia para contestar el problema inicial sobre la oferta de los tenis. Pon mucha atención para lograr descubrir el precio después de aplicar los descuentos mencionados.
“Laura aprovecha las primeras rebajas de fin de año en una tienda para comprarse un vestido que, antes de las rebajas, costaba $450.00; el descuento fue de 15%. En las segundas rebajas, el precio del vestido bajó un 25% adicional. ¿Cuánto pagó Laura al comprar el vestido en las primeras rebajas?”
Para resolver el inciso este problema, debes tener en cuenta que Laura pagará el 85% del valor del vestido, ya que 100% menos 15% es igual al 85%. Acomoda los datos en la relación de proporción, poniendo cuidado de hacerlo correctamente.
$450 entre el costo por pagar es igual a 100% entre 85%.
Aplicando una regla de tres directa, se tiene el precio por pagar es igual a 450 por 85 y el resultado de la multiplicación se divide entre 100. Por lo tanto, se tiene que 38 250 entre 85 da como resultado $382.50, que sería el precio del vestido con la primera rebaja.
¿Cuánto habría pagado se lo hubiera comprado aplicando la segunda rebaja?
En este caso debes considerar el costo anterior, que ahora será tu nuevo 100% y considerar que se le aplicará el 25% de descuento, de ahí la palabra “adicional”.
Teniendo en cuenta que Laura hubiese pagado el 75% del nuevo valor del vestido, ya que el nuevo 100% menos 25% es igual al 75%. Acomoda los datos en la relación de proporcionalidad.
Entonces quedaría $382.5 entre el costo por pagar igual a 100% entre 75%.
Aplicando una regla de tres directa se tiene el costo por pagar es igual a 382.5 por 75 entre 100. Por lo tanto, queda 28 687.5 entre 100 y da como resultado $286.87, que será el costo a pagar por el vestido considerando la segunda rebaja.
¿Cuál es el porcentaje de descuento total en las segundas rebajas con respecto al precio inicial?
Seguramente parece fácil sumar ambos descuentos y aplicar uno sólo al precio total, es decir 15% + 25% es igual al 40% de descuento.
¿Piensas que obtengas el valor encontrado? Haz la prueba.
Toma el valor inicial del vestido, es decir, $450 y descuenta el 40% directamente. Si restas al 100% el 40% entonces lo que debes pagar es el 60%, calcula esa cantidad, de esa forma no habrá necesidad de realizar la resta al final.
Aplicando uno de los procedimientos vistos, multiplica 450 por la representación de 60% como número decimal, en este caso es 0.6. Entonces, 450 pesos por 0.6 es igual a 270 pesos.
Como puedes ver no corresponde al precio que obtuviste antes.
Entonces si los descuentos no deben sumarse, ¿de cuánto fue el descuento real, una vez aplicados ambos descuentos? Para ello compara el valor inicial establecido con el valor pagado después de la segunda rebaja así obtendrás el porcentaje real descontado.
Comienza, 450 entre 286.87 es igual a 100% entre el porcentaje pagado el cual estas buscando.
Aplicando una regla de tres directa tienes porcentaje pagado es igual a 286.87 por 100 y el resultado de la multiplicación se divide entre 450. Por lo tanto, el porcentaje pagado es igual a 63.74 %.
Si restas a 100% el 63.74% que se pagaría en las segundas rebajas tendrías 100% – 63.74% = 36.26%.
Por lo tanto, el descuento real es de 36.26% y no de 40% como se supuso al querer sumar los descuentos desde un principio.
El reto de hoy:
Retoma el problema del reto inicial. ¿Lo recuerdas?
La tienda por inauguración ofrece el 50 por ciento de descuento, más el 30 por ciento de descuento adicional, más el 20 por ciento de descuento extra adicional.
Ahora, ¿piensas que los tenis serán gratis?
Como viste en el problema anterior, los descuentos no se suman y aplican al costo inicial. Se debe aplicar un descuento a la vez, considerando cada vez el precio encontrado como inicial para cada aplicación de descuento.
Ahora aplica los descuentos multiplicando la cantidad inicial por los factores de pagar en un primer momento el 50% por lo tanto sería 50/100, es decir 0.5, el segundo descuento es del 30% por lo tanto pagarás el 70% es decir 70/100 lo que da como factor 0.7, para finalizar el descuento es del 20%, por lo tanto pagarás el 80% quedando 80/100 el factor sería 0.8.
Primer descuento.
($1500) (0.5) = $750
Considerando el nuevo precio, aplica el segundo descuento.
($750) (0.7) = $525
Para finalizar se considera el nuevo costo y aplicas el tercer descuento.
($524) (0.8) = $420
Siendo este último precio que se paga por los tenis ya con los tres descuentos aplicados. Lamentablemente, no son gratis, pero ya conoces la razón.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas