Ecuaciones con paréntesis
Ecuaciones con paréntesis
Aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de ecuaciones lineales.
Énfasis: resolver ecuaciones lineales de la forma ax + b = cx + d, que incluyan uso de paréntesis (propiedad distributiva).
¿Qué vamos a aprender?
En esta sesión continuarás estudiando el aprendizaje esperado: resuelve problemas mediante la formulación y solución algebraica de ecuaciones lineales. Ampliarás tus conocimientos sobre las ecuaciones lineales del tipo ax + b = cx + d, en donde trabajarás ecuaciones que incluyan paréntesis, según lo requiera el problema a resolver.
Se te recomienda que para el desempeño de tus actividades tengas a la mano tu cuaderno u hojas reutilizables, lápiz, goma, regla, tu libro de texto de la asignatura. En caso de tener una discapacidad visual, prepara hojas leyer, un punzón y una regleta.
¿Qué hacemos?
Para comenzar, analiza el siguiente problema. Intenta resolver los cuestionamientos que se plantean a continuación, a partir de lo que ya sabes.
Las dos figuras siguientes tienen el mismo perímetro. La estrella de cinco picos tiene 10 lados iguales que miden 3w + 1.5 y la figura en forma de cruz tiene ocho lados que miden w + 5.25 y cuatro lados que miden w. La actividad consiste en:
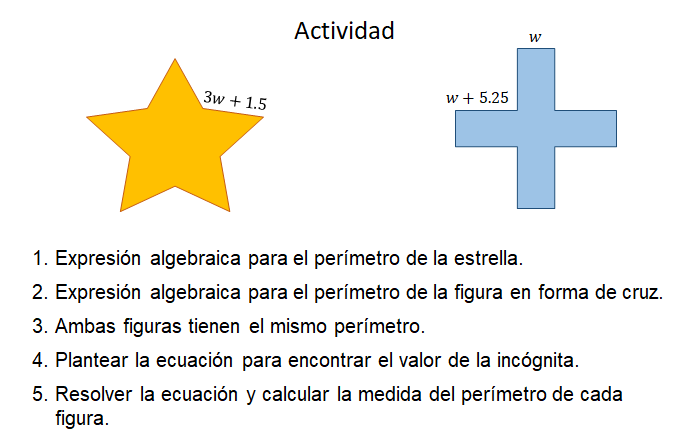
Si ya tienes la respuesta, anótala en tu cuaderno, al finalizar la clase se retomará esta actividad, para ver si lograste encontrar la solución.
Antes de comenzar formalmente la sesión, es importante recordar algunos conceptos e ideas que te ayudarán a resolver los planteamientos que revisarás más adelante.
Recordarás que el planteamiento y resolución de una ecuación es el procedimiento algebraico que se utiliza para resolver problemas cotidianos con las matemáticas.
Está compuesta por un signo igual que divide a las dos expresiones algebraicas equivalentes, compuestas por números, signos de operación y literales, en este caso llamadas incógnitas. Para resolverlas es necesario recordar las leyes y propiedades aprendidas anteriormente.
Algunas de ellas son: las reglas de la adición de números positivos y negativos, la jerarquía de operaciones, las propiedades de la igualdad, la propiedad distributiva y la reducción de términos semejantes.
Recuerdas las reglas de la adición de números positivos y negativos. Si se suman dos números positivos o dos números negativos, se suman los valores absolutos y el resultado conserva el signo de los sumandos.
Por ejemplo: 3 negativo + 5 negativo, es igual a 8 negativo.
Y 3 positivo + 5 positivo es igual a 8 positivo.
Si se suma un número positivo y uno negativo se calcula la diferencia entre los valores absolutos y el resultado conserva el signo del número con mayor valor absoluto.
Por ejemplo: 3 negativo + 5 positivo es igual a 2 positivo y 9 negativo + 5 positivo es igual a 4 negativo.

La jerarquía de operaciones, como su nombre lo indica, te menciona el orden de los pasos a seguir para resolver operaciones combinadas.
En la siguiente ilustración se observa que lo primero que se debe resolver son las operaciones que se encuentran dentro de los signos de operación: primero se eliminan los paréntesis, después los corchetes y, al último las llaves; después se resuelven las potencias y raíces que estudiarás más adelante; enseguida se resuelven las multiplicaciones y divisiones; y, por último, las sumas y las restas, no sin antes recordar que las operaciones del mismo nivel deben resolverse de izquierda a derecha y que, al eliminar signos de agrupación, se sigue el orden mencionado al resolver las operaciones.

También es importante recordar que las propiedades de la igualdad te permiten simplificar una ecuación planteada inicialmente por una equivalente para despejar la incógnita.
Esto es, a partir de realizar lo mismo en cada miembro de la ecuación; es decir, si sumas una cantidad a un miembro de la ecuación debes sumar la misma en el segundo miembro para conservar la igualdad y, así, con cada una de las operaciones que resuelvas; es decir, con la resta, la multiplicación y la división.
Por último, recuerda que también en la resolución de ecuaciones debes agrupar y reducir términos semejantes.
Si dos expresiones algebraicas tienen las mismas literales y el mismo exponente, entonces son semejantes y puedes agruparlas para simplificar la expresión. Por ejemplo:
En la expresión: 3 “x” cuadrada, más 2 ye menos “x” cuadrada, más 6 ye.
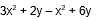
Tienes dos pares de términos semejantes: 2y con 6y y 3×2 con x2. Para simplificar los términos debes sumar o restar según corresponda; en este caso: 3 “x” cuadrada menos “x” cuadrada es igual a 2 “x” cuadrada; es decir, se restan los coeficientes, mientras que la literal y el exponente se conservan.
En la segunda pareja se suman los coeficientes y se deja la misma literal; es decir, 2 ye más 6 ye es igual a 8 ye. Así, te queda la expresión: 2×2 + 8y.
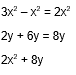
Seguramente, en casa tomaste nota de lo que se acaba de retroalimentar y en este momento recordaste las ocasiones en las que ya has aplicado estos conocimientos. Y bueno, todo lo que recordaste lo utilizarás en esta sesión para resolver los problemas.
El primer planteamiento que se va a resolver es sobre cómo Marco le ayudó a su padre con un problema de su trabajo.
Marco es un alumno de primer grado de secundaria y su papá es un ingeniero químico. Una tarde, Marco vio a su papá sentado en su escritorio, le preguntó qué estaba haciendo; él le respondió que tenía que determinar cuántos galones de una disolución de alcohol al 74 % se necesitan combinar con 5 galones de una disolución de alcohol al 90 % para obtener una mezcla de alcohol al 84 % de concentración.
Marco quiere realizar el cálculo, entonces tomó una hoja y comenzó a resolver el problema considerando los conocimientos que ha adquirido en sus clases de matemáticas.
¿Cómo puede Marco resolver el problema?
Para resolver el problema, Marco decide plantear una ecuación para modelar la situación. Establece que “x” representa el número de galones que se necesitan de la primera disolución, así que lo escribió como 0.74x, que indica el contenido de alcohol que posee dicha mezcla. Luego, construyó una tabla.
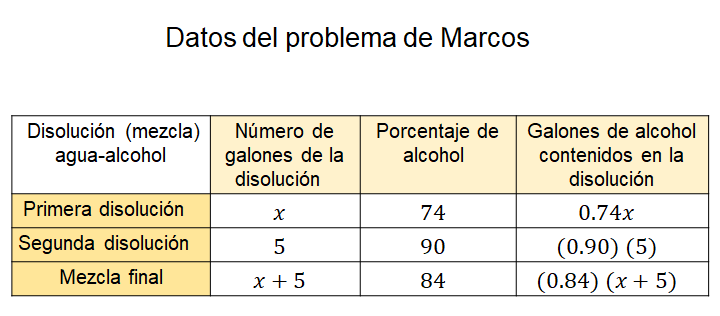
La tabla consta de cuatro columnas: en la primera aparecen las diferentes disoluciones de diferente concentración de alcohol; en la segunda el número de galones de cada disolución; en la tercera el porcentaje de alcohol; y, finalmente, en la cuarta columna el número de galones de alcohol que contiene cada solución.
La primera disolución contiene “x” galones con un porcentaje de alcohol de 74 %, y los galones de alcohol se representan con la expresión 0.74x.
Se puede observar que la segunda disolución contiene 5 galones de disolución con un porcentaje de alcohol del 90 por ciento, de lo cual se obtiene la expresión 0.90 por 5 para calcular la cantidad de alcohol en galones de esa disolución.
En la última fila aparece la mezcla que se quiere hacer; entonces, debe de contener “x” galones de la primera disolución más 5 galones de la segunda disolución para obtener una mezcla de alcohol del 84 por ciento en volumen; por lo tanto, se obtiene la expresión 0.84 por “x” más 5 para representar los galones de alcohol contenidos en la mezcla final.
Hay que ayudar a Marco respondiendo los siguientes cuestionamientos:
- ¿Qué cantidades deben ser iguales en este problema?
- ¿Cuántos galones se requieren para lograr la mezcla final?
- ¿Ya lograste identificar las expresiones que deben ser iguales para plantear la ecuación?
Las expresiones que deben ser igualadas son la suma del número de galones de alcohol contenidos en las dos primeras disoluciones con los galones de alcohol de la mezcla que quiere obtener; por lo tanto, la ecuación que planteó Marco es:
0.74 “x” + 0.90 por 5 igual a 0.84 por la suma de equis más 5.
Así, Marco obtuvo una ecuación de primer grado con paréntesis.

¿Qué es lo primero que se tiene que hacer para resolver la ecuación?
Primero, debes eliminar los paréntesis. En el primer miembro hay que multiplicar 0.90 por 5, obteniendo 4.5.
En el segundo miembro puedes observar que tienes la multiplicación de un monomio por un binomio. Utilizando la jerarquía de operaciones, deberás sumar, primero, lo que está dentro para después multiplicar; pero si observas, no son términos semejantes; por ello, no puedes agruparlos.
¿Qué se puede hacer entonces?
En este caso, se aplica la propiedad distributiva que indica que: si se multiplica un número por una suma, se multiplica dicho número por cada uno de los sumandos y, después, se suman los productos obtenidos.
Del lado izquierdo se aplica la jerarquía de operaciones y se multiplica 0.90 por 5, que es igual a 4.5; y, en el segundo miembro de la ecuación, se aplica la propiedad distributiva y se multiplica 0.84 por “x” más 0.84 por 5, obteniendo 0.84x +4.2.
Ahora se obtiene una ecuación equivalente a la inicial, es decir: 0.74x + 4.5 = 0.84x + 4.2.
Lo que sigue es agrupar términos semejantes del mismo lado de la ecuación; en este caso, se agrupan las incógnitas del lado derecho y los términos independientes del lado izquierdo, utilizando las propiedades de la igualdad. Para ello se resta en ambos dos lados de la igualdad 0.74x y 4.2; al simplificar, se obtiene la ecuación: 4.5 – 4.2 es igual a 0.84x – 0.74x.
Siguiendo con la solución, se tiene que reducir términos semejantes para despejar a la incógnita. Al resolver las operaciones, se tiene 0.3 igual a 0.10x.
Por último, hay que despejar la incógnita, para ello se vuelve a aplicar la propiedad de la igualdad; en este caso, se dividen ambos lados de la ecuación entre 0.10 y así se obtiene que equis es igual a 3.

Lo que indica que el papá de Marco necesita combinar 3 galones de la disolución con 74 % de alcohol, con 5 galones de disolución con 90 % de alcohol para obtener una mezcla con 84 % de alcohol.
Pero, para demostrar que esto es cierto, se tiene que comprobar la solución de la ecuación, sustituyendo a la incógnita, por su valor.
Se sustituye la “x” por 3 en la ecuación y queda la expresión: 0.74 por 3 + 4.5 = 0.84 por 3 + 4.2.
Primero, se resuelve la multiplicación en ambos lados y te queda 2.22 + 4.5 = 2.52 + 4.2.
Al resolver las sumas tienes que 6.72 es igual a 6.72, con lo que se comprueba el resultado del problema y 6.72 representa a la cantidad de alcohol en la mezcla en galones, porque son 8 galones con 84 % de alcohol.
Al calcular 84 % de 8 obtenemos 6.72.

¿Viste cómo Marco sí logró resolver el problema que le planteó su papá con los conocimientos que ha aprendido en la secundaria?
Tú también puedes ayudar a tus familiares aplicando los conocimientos que has adquirido.
Ahora se revisará una situación distinta, se va a calcular en cuántos años la edad de Juan va a ser el doble que la edad de Carlos, si Juan actualmente tiene 42 años y Carlos 18.
Seguramente en otras sesiones has resuelto problemas parecidos, así que ya debes tener una idea para plantear la ecuación.
Pasando del lenguaje común al algebraico: los años que tienen que pasar es el dato que se debe encontrar y se representará con la letra “a”; la edad de Juan, que es 42 más cierta cantidad de años; es decir, 42 + “a” y dos veces la edad de Carlos, que es 18 más, obviamente, la misma cantidad de años que deben transcurrir; es decir, 2 por la suma 18 + “a”.
Por lo tanto, se obtiene la ecuación:
42 + a = 2(18 + a) que es una ecuación lineal con paréntesis.
¿Cuál es la propiedad que se debe utilizar primero para resolver la ecuación?
La propiedad distributiva. Se debe de multiplicar, en el segundo miembro, 2 por 18 y 2 por “a”. Así, la ecuación ahora queda como: 42 + a = 36 + 2a.
Lo siguiente, es utilizar la propiedad de la igualdad para poder agrupar términos semejantes del mismo lado. En ambos miembros de la ecuación, se debe restar 36 y “a” y al simplificar se obtiene: 42 menos 36 es igual a 2a – a.
Reduciendo términos semejantes, la ecuación queda simplificada como 6 = “a”, que es lo mismo que “a” = 6.
Lo que indica que, dentro de 6 años, Juan tendrá el doble de edad que tendrá Carlos.

En casa comprueba la solución de la ecuación, para validar la respuesta.
En 6 años, Juan tendrá 48 años y Carlos 24 y 48 es el doble de 24.

Enseguida, utilizarás este tipo de ecuaciones para resolver situaciones geométricas, observa de qué se trata:
Observa las siguientes figuras.

¿Cuál es la expresión algebraica que modela el área de cada figura?
Si se sabe que ambas figuras tienen la misma área, ¿cuál es la ecuación que modela la situación? ¿Cuál es el valor de x? ¿Cuál es el área de cada figura?
En este caso, se puede observar que los lados de las figuras están dados por expresiones algebraicas y, como dato, se menciona el área; por ello, sería importante que recuerdes cuál es la fórmula para obtener el área de un rectángulo.
Área del rectángulo es igual a base por altura.
Revisa nuevamente, las figuras para responder las preguntas.

En el caso de la figura 1, la base mide 20 y la altura a 3x + 20; así, la expresión que representa el área es: 20 que multiplica a 3x + 20.
Para la figura 2, la base mide 4x + 50 y la altura 10; entonces la expresión algebraica que modela su área es igual a 4x + 50 que multiplica a 10.
Como el problema menciona que ambas figuras tienen la misma área, se pueden igualar para obtener la ecuación: 20, que multiplica a 3x + 20, es igual a 4x + 50, que multiplica a 10.
Una vez obtenida la ecuación se debe resolver utilizando los procedimientos que ya conoces.
¿Observas alguna diferencia entre esta ecuación y las anteriores?
Ahora tienes paréntesis en ambos miembros de la ecuación; por lo tanto, se aplica la propiedad distributiva en ambos miembros. Por un lado, 20 por 3x, que te da como resultado 60x, y 20 por 20, obteniendo 400; del otro lado de la ecuación, 4x por 10, es igual a 40x; y 50 por 10 da 500. La ecuación resultante es: 60x + 400 = 40x + 500. ¿Qué paso sigue?
Se deben agrupar términos semejantes, apoyándote de las propiedades de la igualdad.
En este caso, se resta de manera simultánea en los dos miembros de la ecuación, 40x y 400, obteniendo la ecuación:
60x + 400 – 40x – 400 = 40x + 500 – 40x – 400.
Al reducir los términos semejantes, se obtiene: 20x = 100
Por último, se despeja la incógnita, dividiendo cada miembro de la ecuación entre 20: 20x entre 20 es igual a “x” y 100 entre 20 es igual a 5.
El valor de la incógnita “x” es igual a 5.

Obteniendo la incógnita, ¿ya se resolvió el problema?
No, ¿verdad?
Tienes que comprobar la solución de la ecuación, lo cual te ayudará a encontrar el área de las figuras.
Para ello, tienes que sustituir el valor de la incógnita en la ecuación. Recuerda que la jerarquía de operaciones menciona que hay que resolver primero los paréntesis.
En el primer miembro se multiplica 3 por 5, que es igual a 15; y, en el segundo miembro, 4 por 5, que es igual a 20. Obteniendo 20, que multiplica a la suma 15 + 20, es igual a 20 + 50, que multiplica a 10.
Siguiendo con las operaciones dentro de los paréntesis, se obtiene 15 + 20 = 35 y 20 + 50 = 70. Ahora, se deben resolver las multiplicaciones: 20 por 35 y 70 por 10. En ambos casos, el resultado es 700.
Se comprobó la solución de la ecuación. Así, también sabes que el área de cada figura es de 700 unidades cuadradas y, en efecto, son iguales.

Es así como se resolvió un problema más, utilizando ecuaciones de la forma ax + b = cx + d, empleando signos de agrupación. En estos casos fueron paréntesis, se aplicó la propiedad distributiva, las propiedades de la igualdad y también se aplicó la jerarquía de operaciones.
- ¿Cómo viste el uso del álgebra en la geometría?
- ¿Conoces algún otro problema de geometría que se pueda resolver con ecuaciones?
Anótalo en tu cuaderno y coméntalo con tus compañeras y compañeros, así como con tu profesor o profesora a la distancia.
Ahora, hay que regresar al primer problema que se planteó al iniciar la sesión.
También es un problema de geometría, pero no de área, sino de perímetro.
Recuerda que, para obtener el perímetro de cualquier figura, se debe sumar la medida de todos sus lados.
Entonces, el perímetro de la estrella está dado por la expresión 10 que multiplica a 3w + 1.5; y el de la figura en forma de cruz por la expresión 8 que multiplica a “w” más 5.25, más 4 por “w”.
Como las dos figuras tienen el mismo perímetro, la ecuación que ayuda a encontrar el valor de la incógnita es: 10 que multiplica a 3w, más 1.5, que es igual a 8, que multiplica a w + 5.25, más 4w.
Ahora, para resolver la ecuación se utiliza lo visto a lo largo de la sesión: aplicas la propiedad distributiva: 10 por 3w es igual a 30w y 10 por 1.5 es igual a 15; del otro lado de la ecuación, 8 por w es igual a 8w y 8 por 5.25, es igual a 42; así, te queda la ecuación: 30w + 15 = 8w + 42 + 4w.
En el segundo miembro de la ecuación, se agrupan términos semejantes y se obtiene: 30w + 15 = 12w + 42. Después, se agrupan los términos semejantes del mismo lado; para ello, restas en ambos lados 12w y 15, resultando la ecuación: 18w igual a 27.
Por último, para despejar la incógnita es necesario dividir entre 18 ambos lados de la igualdad. La solución de la ecuación es: w = 1.5.
Ya tienes el valor de la incógnita, ahora debes sustituirla en cada expresión que modela el perímetro de las figuras para obtener la medida numérica.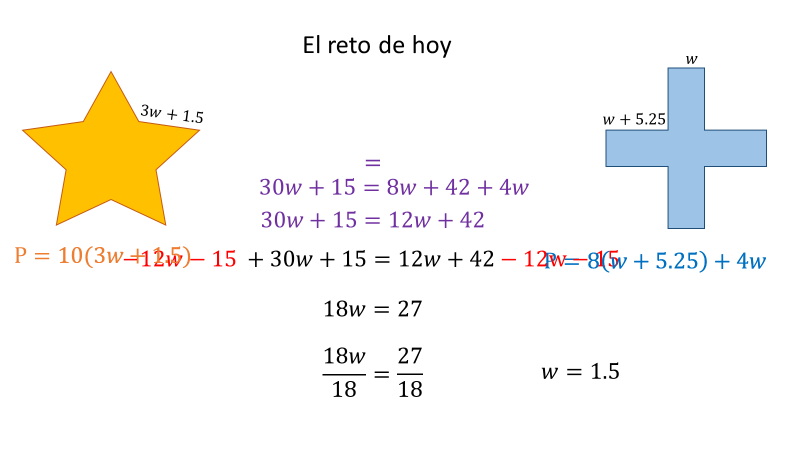
Recuerda que, primero, se resuelven los paréntesis; entonces, como puedes ver, al sustituir a la incógnita por su valor numérico y resolver las operaciones, siguiendo la jerarquía de las operaciones, puedes ver que la igualdad se cumple; por lo que la solución de la ecuación es correcta.
Puedes notar que, en efecto, ambas figuras cuentan con el mismo perímetro, que es de 60 unidades.
Se espera que esta sesión haya sido de mucha productividad para ti.
Has concluido el tema del día de hoy.
El reto de hoy:
No olvides socializar tus dudas con tu maestra o maestro a distancia, en la medida de tus posibilidades, y consultar tu libro de texto u otras fuentes para practicar la solución de ecuaciones lineales de la forma ax + b = cx + d que incluya el uso de paréntesis para aplicar la propiedad distributiva.
Asimismo, no olvides dar respuesta a las siguientes preguntas y revisarlas con tus compañeros y profesora o profesor de esta asignatura. - ¿Cómo viste el uso del álgebra en la geometría?
- ¿Conoces algún otro problema de geometría que se pueda resolver con ecuaciones?
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas