Relaciones de variación lineal.

Relaciones de variación lineal.

Aprendizaje esperado: analiza y compara situaciones de variación lineal a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación.

Énfasis: interpretar y resolver problemas que se modelan con variación lineal.

¿Qué vamos a aprender?

Aprenderás a analizar, interpretar y resolver situaciones de variación lineal. Estas situaciones se pueden presentar de diferentes maneras.

¿Qué hacemos?

Para iniciar, recordarás que una relación de variación lineal es aquella que vincula dos variables que, al ser representadas gráficamente, forman una línea recta.

Ya has aprendido a identificar la constante de variación de una situación a partir de los datos concentrados en una tabla. Esto te permite representar algebraicamente estas relaciones y encontrar los valores faltantes.

Las siguientes relaciones son ejemplos entre dos tipos de magnitudes que varían linealmente:

• La distancia recorrida por un taxi en un viaje y el costo del viaje.
• Volumen de un líquido (por ejemplo, gasolina) y su precio.
• La base de un triángulo equilátero y su perímetro.
• El lado de un cuadrado y su perímetro.
• La compra de boletos para asistir al cine y su costo.
• El pago de servicio de agua.
• La compra de varias piezas de un mismo producto.

¿Te has dado cuenta cómo una cantidad se relaciona con la otra cantidad o cómo una magnitud varía con relación a la otra magnitud? ¿Se te ocurren otras situaciones en las que se presente una relación de variación lineal?

En relaciones de variación lineal, las cantidades que cambian se llaman variables y las cantidades que se mantienen fijas se llaman constantes. En estos casos, cuando se conoce el valor de una variable, es posible determinar la otra.

Las situaciones mencionadas y muchas más se pueden representar en tablas de frecuencias, con una expresión algebraica, e interpretar su comportamiento en una gráfica para su análisis.

Por ello, es importante aprender a analizar esta información y poder ir de una representación a otra.

Además, debes tener en cuenta que una variable es una característica que toma diferentes valores; es decir, que cambia. Considerando dos variables numéricas que se relacionan; se dice que tienen una relación de proporcionalidad directa si cumplen dos condiciones.

1. Cuando una variable toma el valor de cero, la otra también vale cero.
2. Cuando una variable se incrementa o disminuye en una cantidad fija, la otra variable también se incrementa o disminuye en la misma proporción.

Analiza y reflexiona la siguiente situación. “La compra de litros de gasolina y el costo a pagar del producto”.

En una bomba de gasolina se observan varias pantallas con números que proporcionan información a los clientes. Conforme el despachador va llenando el tanque de gasolina, una pantalla indica la cantidad de litros de gasolina vertidos en el tanque del auto y otra marca el precio (en pesos) que se tiene que pagar por esa cantidad de gasolina. Una tercera pantalla permanece con un número constante durante la operación e indica el precio de un litro de combustible, como se muestra en la figura.

Responde las preguntas.

Si analizas la imagen de la situación, encontrarás los siguientes datos:

• Venta total ($364.06).
• Litros vendidos (21.8).
• Precio por litro de gasolina ($16.70).

Si observas la situación, representa una relación de proporcionalidad directa. En este caso, las dos variables que intervienen son los litros suministrados o vendidos y la venta total. La venta depende de los litros de gasolina que se adquieran; así se tendrá la siguiente expresión que modela el problema:

y = 16.70x

Donde “y” es la variable dependiente que representa el pago total de la venta; “x” es la variable independiente que representa los litros que se compran o suministran a un vehículo y, en este caso, la constante 16.70 pesos, que es el precio por litro del combustible.

Con la expresión anterior se puede encontrar cualquier valor de la variable (y) (venta total) para cualquier cantidad de litros vendidos y, al mismo tiempo, tabular la relación que existe entre las variables como a continuación se muestra.

Se sabe que por un litro de gasolina se debe pagar $16.70. A partir de esta referencia, se puede encontrar el total de venta conociendo la cantidad de litros vendidos. Por ejemplo, para obtener cuánto se paga por 0, 1, 5, 8, 13, 17, 24, 36 litros, etcétera, se multiplica el número de litros vendidos por el precio por litro; así se tiene que:

¿Cómo vas hasta aquí?

Para contestar la primera pregunta, se identifican las dos variables involucradas en el problema y se calcula lo que se paga por 36 litros de gasolina.

Ahora se trazará la gráfica de la relación entre las dos variables, que describen la situación “litros vendidos” y “venta total”. Para esto, se utilizará un plano cartesiano.

Las expresiones algebraicas de la forma y = ax, asociadas a una situación de variación proporcional, se pueden representar en el plano cartesiano mediante líneas rectas que pasan por el origen; esto es, el punto (0, 0). El valor de la letra “a” se le llama pendiente de la recta.

Entre mayor sea el valor de la pendiente de una recta, su ángulo de inclinación respecto al eje “x” será mayor y viceversa.

A continuación, se muestra la gráfica que modela la situación y que corresponde a la expresión algebraica “y=16.70x”. En el eje “x” se representan los litros vendidos, y en el eje “y”, el total de la venta.

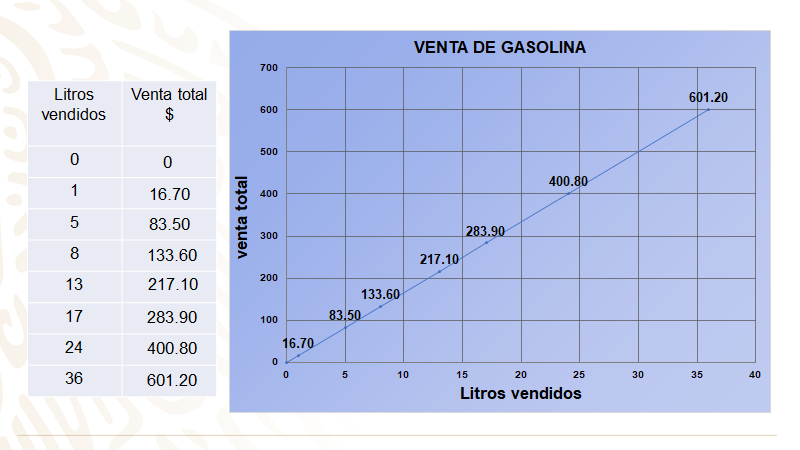
Como se puede observar, la gráfica es representada por una recta que pasa por el origen, ya que la relación es lineal y de proporcionalidad directa. Cada punto sobre la recta forma parte de la pareja de valores (“x”, “y”), que corresponden a la relación.

Ahora responde la última pregunta planteada al inicio, si un cliente pagó $654.64, ¿cuántos litros de gasolina cargó?

¿Qué operación va a permitir resolver este cuestionamiento?

A partir de la expresión algebraica que modela la situación, que es “y = 16.70x”, y al sustituir “y” por el valor conocido 654.64, te queda la ecuación lineal 654.64 = 16.70x.

En este caso, se debe de realizar el despeje de la variable “x” aplicando las propiedades de la igualdad.

Observa que, para poder encontrar el valor de “x”, es necesario dividir ambos miembros de la igualdad entre 16.70, ya que este dato está multiplicando a “x” en el segundo miembro de la ecuación.

Se tiene que 654.64/16.70= 16.70x/16.70.

Resolviendo las divisiones se obtiene que 654.64 entre 16.70 es igual a 39.2 y, por otro lado, 16.70x entre 16.70 es igual a “x”.

Así se tiene que 39.2 = x.

Al reordenar el despeje de “x”, queda como x = 39.2.

Entonces se concluye que el cliente pagó $654.64 cuando compró 39.2 litros de gasolina.

Como pudiste observar, en las situaciones que involucran una relación lineal, se puede obtener una expresión algebraica, una tabla que relaciona a la pareja de valores y una gráfica para analizar su comportamiento.

Analiza la siguiente situación para identificar mejor estas particularidades.

En cierta ciudad, la tarifa del servicio de taxis se fijó en $8.74 como cantidad base (“banderazo”) para los taxímetros, y de $1.30 por cada 250 metros recorridos o bien, por cada 45 segundos transcurridos. Cuando una de estas dos cosas sucede, el taxímetro aumenta $1.30. A esta acción se le conoce como “brinco”.

Completa la siguiente tabla a partir de la información anterior.

La tabla está conformada por cuatro columnas. En la primera columna se tiene la cantidad de brincos; en la segunda columna está el costo por determinado número de brincos; en la tercera columna se encuentra el banderazo, que es la cantidad fija que se tiene desde el inicio del recorrido, y por último, en la cuarta columna, se tiene el total a pagar de acuerdo con el número de brincos dado en cada caso.

Revisa cada espacio y analiza el comportamiento que tiene esta situación.

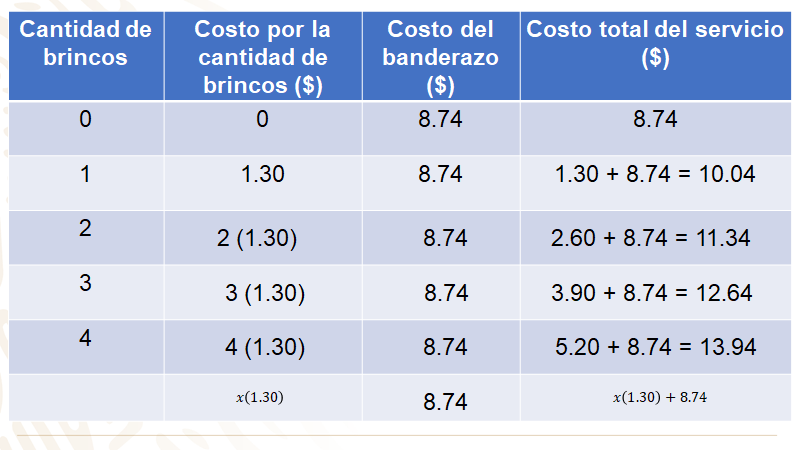
Al iniciar el viaje, es decir, cuando el número de brincos es cero, el costo será de 8.74.

Para un brinco se tiene que el costo es de 1.30 pesos más el costo del banderazo, 8.74 pesos, es igual a $10.04.

Para 2 brincos se tiene 2 por 1.30 pesos, que es igual a 2.60 pesos, más 8.74 pesos, igual a $11.34 pesos; para 3 brincos, 3 por 1.30 pesos, más 8.74 pesos, es igual a 12.64 pesos. Ahora, cuando se realizan 4 brincos, se tiene que el costo del servicio es 5.20 pesos, más 8.74 pesos, igual a 13.94 pesos.

¿Cómo puedes saber lo que se paga por el servicio para “x” número de saltos?

En este caso, se multiplica “x” por 1.30 pesos, que es el costo por brinco y al resultado se le suman 8.74 pesos, quedando la expresión algebraica “x por 1.30 + 8.74”.

Analiza la información que tienes.

En la tabla se observa que el costo de un viaje depende de la cantidad de brincos (“x”) que da el taxímetro, y esto se representa como “x” por 1.30; el banderazo, 8.74, es una constante que se suma al número de brincos, para obtener el costo del servicio de taxi.

Si se representa el costo de un viaje con la literal “y”, la expresión algebraica que representa la situación es “y=1.30x+8.74”.

Esta expresión te permite encontrar el costo de un viaje a partir de los brincos que dé el taxímetro en un recorrido.

La situación anterior se puede representar mediante la gráfica asociada a una relación lineal de la forma “y=ax+b”.

Conociendo los valores de la situación, se analizará la gráfica para ver cómo se da la razón de cambio.

Para 0 cero brincos, 8.74 pesos; para 1 brinco, 10.04 pesos; para 2 brincos, 11.34 pesos; para 3 brincos, 12.64 pesos; para 4 brincos, 13.94 pesos; para 5 brincos, 15.24 pesos, y así sucesivamente.

La representación gráfica es una recta que interseca al eje de las ordenadas, pero no pasa por el origen; entonces no es una relación de proporcionalidad directa. La constante “b” indica el punto de intersección de la recta con el eje “y”, y se conoce como ordenada al origen. Por ejemplo, en la gráfica se representa la expresión “y=1.30x 8.74”, donde “b” es igual a 8.74, por lo que las coordenadas (0, 8.74) es el punto de intersección entre la recta y el eje de las ordenadas.

La ordenada al origen de una relación de variación lineal siempre corresponde a las coordenadas (0, b).

En una relación de variación lineal, la razón de cambio es la medida en la cual una variable de modifica con relación a la otra. En este caso, ¿cuál es la razón de cambio en esta gráfica?

En una relación de variación lineal, la razón de cambio es constante, y en este caso es 1.30, e indica cómo cambia “y”, con relación a la variable “x”.

Resuelve una nueva situación de variación lineal.

A un recipiente vacío se le agrega cierta cantidad de agua, y la masa del recipiente más el agua es de 50 gramos. Después se agrega otra porción de agua idéntica a la anterior, ahora el recipiente y el líquido suman 70 gramos de masa.

La tabla muestra los datos anteriores.

¿Cuál es la masa del recipiente vacío? ¿Cuál es la razón de cambio de la situación? ¿Cuál es la masa del recipiente si se agregan 3, 4 y 5 porciones de agua?

Se sabe que de 1 porción a 2 porciones de agua la masa aumenta 20 gramos; por lo tanto, a 50 gramos se le resta 20 y así se obtiene la masa del recipiente, que es de 30 gramos; es decir, para cero porciones de agua, la masa es de 30 gramos.

La diferencia de 20 gramos entre una porción y otra determina la razón de cambio en esta relación. Con esto puedes saber que la masa para 3, 4 y 5 porciones es de 90, 110 y 130 gramos, respectivamente.

Como se sabe, la regla general de una relación con variación lineal, la expresión general es “y = ax + b”.

A partir de la expresión general y los valores que se obtuvieron en la tabla, se plantea la regla o expresión algebraica de esta situación entre las porciones de agua (x) y la masa del recipiente (y).

Si te das cuenta, la razón de cambio, que es 20, es la que multiplica el número de porciones de agua; mientras que la constante 30, representa la masa del recipiente vacío y es una constante. Por lo tanto, la expresión de esta situación es:

“y = 20x + 30”.

En casa, construye la gráfica que representa la situación e identifica la ordenada al origen, es decir, la coordenada (0, b) y la razón de cambio de la relación de variación lineal vista.

Analiza un par de situaciones similares y compáralas con la anterior.

Considera el mismo recipiente de la situación anterior, pero ahora se le agregan porciones de 40 gramos.

Los valores obtenidos al agregar diferentes porciones iguales de agua los muestra la tabla. Para 1 porción la masa es de 70 gramos; para 2, es de 110 gramos; para 3, es de 150; para 4, de 190, y para 5 porciones es de 230 gramos.

Al hacer este cambio de la medida de las porciones de agua, ¿cambió la masa del recipiente vacío?

No cambia, porque el recipiente es el mismo. Lo único que se modifica es su razón de cambio, que, en lugar de ser de 20 g, ahora es de 40 g. Por lo tanto, su regla de correspondencia es “y = 40x + 30”.

¿Cómo será la pendiente o inclinación de la recta de esta relación en comparación de la anterior?

Anota tus respuestas para validarlas más adelante.

Observa una nueva situación relacionada con las anteriores.

Un recipiente que tiene una masa de 60 g se llena con porciones de agua de 30 gramos, equivalentes a las porciones de la primera situación plateada en este contexto.

La tabla muestra la masa del recipiente para 1, 2, 3, 4 y 5 porciones de agua.

¿Ya tienes la respuesta a las preguntas?

En este caso, ¿cuál sería la expresión algebraica de correspondencia con la situación? ¿Cuál variable se modificó con respecto a la primera situación?

Partiendo de los datos mencionados, se puede deducir que la regla de correspondencia es “y = 20x + 60”, en donde el factor que cambia es la masa del recipiente vacío y el que se conserva es la razón de cambio que es de 30 gramos.

Considerando la ordenada al origen y la pendiente, ¿cómo será la gráfica de esta relación en comparación con las dos anteriores?

Construye la gráfica en tu cuaderno para poder responder a la pregunta.

Analiza la gráfica de las tres, tomando como referencia la primera situación.

¿Qué ocurre con la recta de la situación 4 cuando las porciones de agua aumentan su masa? Al graficar ambas rectas en el mismo plano puedes observar que la recta tendrá una inclinación mayor que la de la situación 3, es decir, la razón de cambio es mayor, pero ambas cortan al eje de la “y” a la altura del 30.

¿Qué ocurre con la recta de la situación 5, en donde se cambia el recipiente por uno más pesado?

La recta tiene la misma pendiente o razón de cambio que en la situación 3; sin embargo, corta al eje de las “y” a la altura del 60 y no a la altura del 30, como en la primera situación.

A partir del análisis anterior, se puede concluir que el valor constante de la regla de correspondencia es el que indicará dónde comienza la recta o a qué altura corta al eje de las “y”, mientras que el factor de cambio o pendiente va a indicar la inclinación de la recta con respecto al eje “x”.

Cada vez que se te presente una situación similar a las revisadas en esta sesión, podrás resolverlas completando la tabla de correspondencia entre ambas magnitudes o cantidades involucradas, obteniendo la expresión algebraica que modela cada situación trabajada, y construyendo la gráfica correspondiente a cada tabla de valores.

Si quieres saber más sobre el tema acércate con tu profesora o profesor de esta asignatura.

Has concluido el tema del día de hoy.

El reto del hoy:

En tu libro de Matemáticas de primero de secundaria ubica el tema y resuelve los problemas que se relacionen con el tema estudiado el día de hoy.

¡Buen trabajo!

Gracias por tu esfuerzo.

Para saber más:

Lecturas

https://libros.conaliteg.gob.mx/secundaria.html