En busca del enésimo término

En busca del enésimo término

Aprendizaje esperado: formula expresiones algebraicas de primer grado a partir de sucesiones y las utiliza para analizar propiedades de la sucesión que representan.

Énfasis: identificar los enésimos términos que se generan a partir de la fórmula general de una sucesión aritmética.

¿Qué vamos a aprender?

Trabajarás un tema relacionado con las sucesiones y las expresiones algebraicas; verás cómo, a partir de una regla, puedes encontrar el enésimo término de una sucesión aritmética.

¿Qué hacemos?

Recuerda que una sucesión es un conjunto ordenado de elementos que se identifican por tener una regla en su secuencia. Analiza el siguiente ejemplo, en el que puedes representar los datos con una sucesión de números e identificar sus características:

El agua a temperatura ambiente tiene 20 grados Celsius, aproximadamente, dependiendo del lugar o la zona en la que se encuentre; ahora, piensa que vas a someter una cierta cantidad de agua a fuego constante que elevará poco a poco su temperatura, y tomarás registro cada minuto.

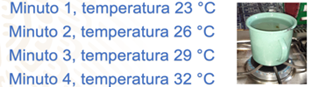
¿Cuál será la temperatura del agua al minuto 5?, ¿se puede saber a los cuántos minutos el agua empezará a hervir? Ten en cuenta que la temperatura del punto de ebullición del agua, es decir, el momento en el que empieza a hervir, a nivel del mar, es de 100 grados Celsius, por lo que esta temperatura será el referente.

Es importante mencionar que supondremos, que en algún momento, la temperatura dejará de aumentar, por lo que, si la temperatura aumenta de manera constante, y se sabe cuál es el límite, se puede decir que se trata de una progresión que también es una sucesión, pero finita.

Determinaremos si existe un patrón en la forma en que la temperatura del agua aumenta, en relación con el tiempo, para así contestar la primera pregunta.

Reflexiona ¿Cómo podrías observar si hay un patrón entre el tiempo que transcurre y la temperatura del agua al someterse al fuego?, ¿qué significa que el fuego sea “constante”?

Puedes organizar la información en una tabla para tu comprensión y análisis.

Observa: en la primera fila, se encuentran los minutos que corresponden al tiempo que el agua está en el fuego; y en la segunda fila la temperatura del agua.

Con los datos que del problema completaremos la tabla. Recuerda que el fuego se mantiene constante.

Con la tabla puedes observar que hay un patrón de aumento en el tiempo y en la temperatura del agua. La diferencia de la temperatura del agua entre un minuto y otro es de 3 grados. Significa que hay un aumento constante en el tiempo, y la temperatura del agua al calentarse.

Para el siguiente minuto, el minuto 5, el agua aumenta 3 grados en su temperatura con respecto al minuto 4. Observa:

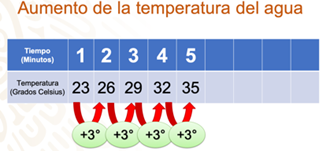
Por lo que podemos anticipar que para el minuto 5 habrá aumentado 3 grados, y el agua tendrá una temperatura de 35 grados, como puedes ver registrado en la tabla.

Has analizado que la temperatura del agua aumenta de manera constante 3 grados cada minuto. Al representar como una sucesión de números la temperatura del agua. Lo que representa una “sucesión aritmética”, ya que la diferencia entre dos valores consecutivos siempre es la misma.

Sucesión aritmética

Es una serie ordenada de figuras o números, donde la diferencia entre dos valores consecutivos, llamados términos, es constante; es decir, siempre es la misma.

Ahora que ya tienes la definición de “sucesión aritmética”, retoma la pregunta planteada al inicio de la sesión: ¿Podríamos saber a los cuántos minutos el agua comenzará a hervir?

Por supuesto que sí, ya que es una sucesión ordenada de números bastaría con ir sumando de 3 grados en 3 grados hasta llegar a 100 grados, pero eso sería un proceso largo. Para eso elaboraremos 2 tablas: en la primera, para representar la suma de 3 en 3 de manera simplificada, lo haremos con una multiplicación, donde llamaremos “n” al tiempo en minutos. Así, tenemos que después de un minuto, la temperatura aumentó 3º a los 2 minutos, 3 por 2 igual a 6º, y así sucesivamente. La segunda tabla es la que ya viste antes, representa la temperatura del agua.

Observa que entre los productos de la primera tabla y sus respectivos valores, en la segunda tabla, siempre hay una diferencia de 20.

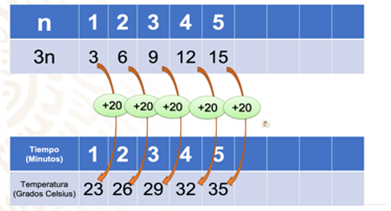
Es decir: a 3n se le suman 20, en cada caso, para obtener la temperatura del agua de acuerdo con el tiempo transcurrido. De 3 a 23 hay que sumar 20; de 6 a 26 hay que sumar 20, y así entre 9 y 29, 12 y 32, 15 y 35.

Esta idea te ayudará a obtener la regla de una sucesión. Así como en el perímetro y el área se usan expresiones algebraicas, también estas sucesiones se pueden generalizar con una expresión, que nos muestra las características de esta sucesión.

Identifica que el aumento o crecimiento, en este caso, va de 3 en 3. Posteriormente, con la comparación de la tabla, observa que la diferencia entre los respectivos valores de la tabla original, con la tabla del 3, siempre es de 20. Por lo que la sucesión va de 3 en 3, más 20, para ajustar a la sucesión de números que representan los valores de la temperatura.

Ahora, si consideramos a la literal “n” como el tiempo en minutos o, en este caso, los términos de la sucesión, y la literal “a” es la temperatura del agua en “n” minutos, entonces obtenemos la expresión algebraica:

“a” es igual a: 3 por “n”, más 20.

Entonces, con la expresión algebraica podemos calcular la temperatura del agua para cualquier minuto, sin tener que sumar tantas veces el 3. Por ejemplo, vamos a calcular la temperatura del agua al minuto 20:

La expresión algebraica establecida es: “a subíndice n” = 3n + 20, donde “a subíndice n” representa cualquier término de la sucesión y “n” son los minutos transcurridos. Ahora, si queremos saber cuál es el término 20, es decir, la temperatura a los 20 minutos, entonces sustituimos “n” por 20 en la regla; multiplicamos y resolvemos las operaciones:

Puedes comprobar que la expresión nos dará la temperatura del agua, en cualquier minuto que elijamos.

Por ejemplo, para el minuto 4 que es un dato que ya tenías, multiplicamos 3 por 4, es igual a doce, y sumamos 20; que nos da como resultado 32. Dato con el que ya contábamos, es decir, al minuto 4 la temperatura del agua será de 32 ºC.

Ahora, sólo falta responder: ¿a los cuántos minutos el agua empezará a hervir?

Ya viste que a los 20 minutos el agua alcanza 80 grados Celsius de temperatura, así que necesitamos calentarla por más tiempo. Podríamos utilizar la misma expresión algebraica para calcular el tiempo.

La expresión algebraica queda: “a subíndice n”, es igual a 3 que multiplica a “n” más 20. En esta expresión, “a subíndice n” es el valor del enésimo término de la sucesión, en este caso corresponde al valor de la temperatura, dato que ya conocemos que es 100 grados Celsius. Sustituimos el valor de “a subíndice n” por 100 grados en la regla, y resolvemos:

Obteniendo como resultado 26.6, que es un número decimal periódico. Para responder podríamos decir que, si el agua se mantiene a fuego constante, entre el minuto 26 y el 27, el agua estará hirviendo.

Ahora analiza la siguiente situación:

Como sabes, realizar actividades físicas nos ayuda a mantenernos sanos. Los ejercicios isométricos son actividades corporales que implican activar un músculo, o un grupo de músculos, mientras nos mantenemos estáticos en una postura, durante un tiempo específico. La siguiente situación es acotada a ciertas condiciones.

Mónica ha empezado a realizar ejercicios isométricos, en específico la sentadilla estática en el aire; ésta consiste en: Mantenerse con las piernas flexionadas, sin apoyo, como si se sentara en una silla imaginaria, pero manteniéndose en el aire.

Mónica se ha propuesto fortalecer los músculos de su espalda, ya que está recuperándose de una lesión, y ha realizado un programa de entrenamiento para lograr mantenerse 10 minutos en esa posición. Mónica realizó el programa de entrenamiento para los 7 días de la semana: el primer día debe mantenerse 15 segundos; el segundo día, 20 segundos; el tercer día, 25 segundos; y así sucesivamente, hasta lograr su meta de mantenerse en esa posición durante 10 minutos.

Es importante mencionar que, en algún momento, el mantener la posición durante cierto tiempo de manera constante tiene un límite; se puede decir que se tiene una progresión, que también es una sucesión, pero finita.

Te sugerimos que escribas en tu cuaderno las siguientes preguntas para reflexionar.

• ¿Cuántos segundos permanecerá Mónica en sentadilla estática cada día de los primeros 7 días?
• ¿Cuántos segundos permanecerá en el día 20 de su entrenamiento?
• ¿Cuántos días necesitará Mónica para lograr su meta de 10 minutos?

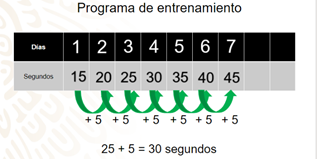
Para tener una mejor organización del programa de entrenamiento de Mónica, realiza una tabla, como la que se muestra a continuación:

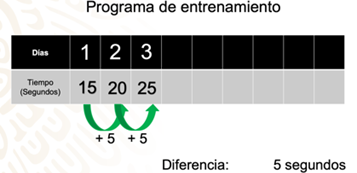
Observa, en la primera fila se encuentran los días que corresponden al entrenamiento, y en la parte inferior los segundos que permanece en esa posición.

Con esta información podemos completar la tabla de entrenamiento de Mónica: En el día 1, los segundos de duración de la rutina son 15; el día 2, los segundos son 20; el día 3, los segundos son 25.

¿Cuál es la diferencia que hay entre los segundos de duración de la rutina y los días?

Como puedes ver, la diferencia es 5: cada día se va incrementando en 5 segundos. Con esta información puedes dar respuesta a la primera pregunta: ¿cuántos segundos permanecerá Mónica en sentadilla estática durante los primeros 7 días?

Como podemos ver en la tabla, por día se van incrementando 5 segundos: ¿cuántos segundos se mantuvo Mónica en sentadilla estática en el cuarto día?

¡Correcto! 30 segundos: sumamos los segundos del tercer día, que son 25 más el incremento que es 5; para encontrar el valor del cuarto día y del quinto día son 35 segundos; del sexto día 40 segundos, y del séptimo día 45 segundos. Ya contestamos la primera pregunta. ¿Cuántos segundos permanecerá Mónica en sentadilla estática cada día de los primeros 7 días? 15, 20, 25, 30, 35, 40 y hasta 45 segundos.

Para calcular la respuesta a la segunda pregunta: ¿cuántos segundos permanecerá en el día 20 de su entrenamiento? Incrementar de cinco en cinco hasta llegar al día 20 puede tomar algo de tiempo, así que para simplificar el trabajo encontremos la expresión algebraica que representa esta sucesión, ya que nos ayudará a encontrar, de manera más sencilla, ese dato.

Para establecer la expresión algebraica, a la que se conoce como “Regla General”, nos guiaremos de la siguiente estructura:

Diferencia que multiplica a “n”; esta literal representa el valor o término que estamos buscando. En este caso ya conocemos la diferencia, que es 5 segundos. Y “n”, en este caso representa a los días; entonces, hasta el momento, la regla general sería: 5 que multiplica a n; es decir, 5n que nos indica cómo se incrementa el tiempo día con día.

Verifiquemos la regla general al sustituir el primer valor de “n”, que en este caso es 1, y multiplicarlo por 5, nos debe dar como resultado 15 segundos. Por lo que efectuamos el producto 5 por 1, es igual a 5. No nos dio 15 segundos, ¿qué falta hacer? ¿Qué operación debemos realizar para que nos dé como resultado 15 segundos?

¡Correcto! Una suma: a 5 debemos sumarle 10 para conseguir que nos dé como resultado 15. Ahora, hagamos lo mismo con el segundo valor de “n”, que es 2: multipliquemos 5 por 2, es igual a 10. Ahora, ¿cuánto debemos sumarle a 10 para que nos dé como resultado 20 segundos?

¡Correcto!, otra vez tendremos que sumar 10; entonces, para que la regla general se cumpla, debemos sumarle 10 a cada término. Por lo tanto, la regla general de esta sucesión es: “a subíndice n” = 5n + 10.

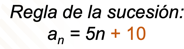
Con esta regla ya puedes responder la segunda pregunta: ¿cuántos segundos permanecerá en posición de sentadilla estática el día 20 de su entrenamiento?

Para ello, se sustituye el valor en “n”, que representa los días de entrenamiento; en este caso el valor de 20 y se multiplica por el valor de la diferencia, que es 5, dando como resultado 100; ahora suma 10, el resultado es 110, que representa los segundos que permanecerá Mónica en sentadilla estática en el día 20 de su entrenamiento.

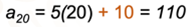
Ya establecimos la regla general para encontrar los segundos que se mantendrá Mónica en sentadilla estática, por cada día de entrenamiento, que es “a subíndice n” = 5n + 10, en la que “a subíndice n” representa el enésimo término de la sucesión, es decir, el tiempo en segundos para “n”.

Ahora, ¿cuántos días necesitará Mónica para lograr su meta?

Lo primero que deberemos analizar es si la regla general que encontramos para obtener los segundos sirve para encontrar los días.

En la regla sustituimos “a subíndice n” por su valor numérico, que en este caso es 600, ya que 600 segundos equivalen a 10 minutos. Así, podemos plantear una ecuación de primer grado y encontrar cuántos días le tomará a Mónica completar su meta. La ecuación de primer grado es: 5n + 10 = 600.

Para resolver la ecuación, haremos uso de la propiedad uniforme: primero restamos 10 en ambos miembros de la igualdad:

Para despejar “n” volvemos a aplicar la propiedad uniforme, y dividiremos ambos miembros de la ecuación entre 5.

Así que Mónica cumplirá su meta en 118 días.

Repasa algunos conceptos para entender mejor este tema:

• Una “sucesión” es un conjunto ordenado de elementos que se identifican por seguir una regla o patrón.
• A los elementos de una sucesión se les conoce como “términos”. Cuando la diferencia entre términos consecutivos es constante, se trata de una “sucesión aritmética”.
• Las sucesiones aritméticas tienen una regla general que es:

= dn + b

En la que “n” representa cualquier término de la sucesión, “d” la diferencia entre términos consecutivos y “b” la cantidad que se suma o resta. En este caso, “d” y “b” son constantes.

Con esta síntesis de la información podrás resolver los siguientes ejercicios. Aplicando la regla general.

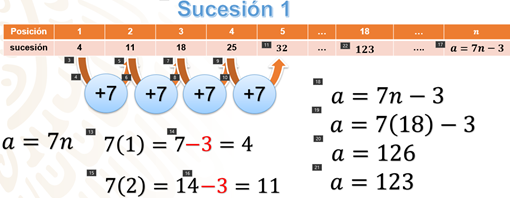
Anota las siguientes sucesiones, encuentra la siguiente posición, la posición indicada en la tabla y la enésima posición.

Vamos a encontrar la regla de la sucesión, a partir de la información de la tabla.

Puedes ver que la diferencia entre términos consecutivos es 7; por lo tanto, ya tenemos el valor de “d”, y lo colocamos donde corresponde, en la expresión general de la sucesión. Ahora, si multiplicamos 1 por 7 podemos ver que nos falta 1 para obtener el valor del término 1, por lo tanto, uno es el valor que le corresponde a “b”; es decir, el número que se suma.

Por lo tanto, en este caso, el término “n” es igual a: 7 por n más uno. Con esto ya podremos resolver los siguientes ejercicios:

Anota las siguientes sucesiones, encuentra la siguiente posición, la posición indicada en la tabla y la enésima posición.

En la primera tabla tenemos los términos del 1 al 4, cuyos valores son: 4, 11, 18 y 25, respectivamente. Hay que encontrar el siguiente término, el término 18 y el enésimo término.

Para la segunda tabla los valores de los primeros cuatro términos son: 13, 24, 35 y 46, respectivamente. Hay que encontrar el término 5, el término 12 y el enésimo término.

Determinaremos la diferencia entre términos consecutivos en cada caso, y observaremos que sea constante. Después, buscamos el valor que se tiene que sumar o restar para ajustar a los valores de la tabla en cada sucesión, y así, al tener el enésimo término, podremos encontrar los términos que nos faltan.

La diferencia entre términos consecutivos es 7, y a este número se le restan 3 para obtener el valor del primer término de la sucesión. Entonces, tenemos que cuando “n” es igual a 1, su valor es: 7 ( 1 ) – 3 = 4. Cuando es 2: 7 ( 2 ) – 3 = 11. Así, podemos obtener la enésima posición con la regla, = 7n – 3, y ahora podemos encontrar los términos 5 y 18.

= 7 ( 5 ) – 3

= 35 – 3

= 32

La humanidad siempre ha tratado de encontrar patrones: el tiempo que tarda la Luna en volver a reflejar la luz del Sol por completo; las estaciones del año; incluso la forma en que se reproducen los animales. Como te puedes dar cuenta, buscamos descifrar las reglas que controlan y describen todo lo que vemos, y este tema es una muestra de la necesidad de entender y explicar los diversos sucesos.

No cabe duda de que las matemáticas pueden estar presentes en muchos aspectos de la vida cotidiana; consulta en tu libro de texto el tema de sucesiones, verás que hay situaciones que podrás resolver, como las que revisaste en esta sesión.

El reto de hoy:

El reto será encontrar los valores para completar la segunda tabla, únicamente te adelantamos la regla; tu tendrás que encontrar los términos que faltan y comparar sus resultados para ver si son los números correctos.

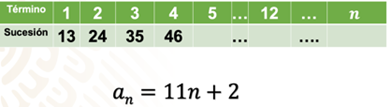
Te corresponde completar la tabla para encontrar las posiciones 5 y 12.

¡Buen trabajo!

Gracias por tu esfuerzo.