Problemas de comparación de fracciones
Problemas de comparación de fracciones
(Clase de Repaso)
Aprendizaje esperado: convierte fracciones decimales a notación decimal y viceversa. Aproxima algunas fracciones no decimales usando la notación decimal. Ordena fracciones y números decimales.
Énfasis: ubicar fracciones y decimales en una recta numérica, y resolver problemas que impliquen comparar fracciones y decimales.
¿Qué vamos a aprender?
Resolverás problemas relacionados con la ubicación, y la comparación de fracciones y decimales.
¿Qué hacemos?
Comenzaras con un poco de historia sobre las fracciones y los números decimales. Para ello, observa el siguiente video del minuto: 00:25 a 02:51
- La historia de las fracciones y los números decimales
Ya conoces diferentes situaciones de la vida cotidiana en donde se utilizan y se encuentran tanto las fracciones como los decimales. Anteriormente aprendiste cómo identificar una fracción o bien un número decimal en la recta numérica. Puedes saber en qué punto de la recta numérica se encuentra 7/5
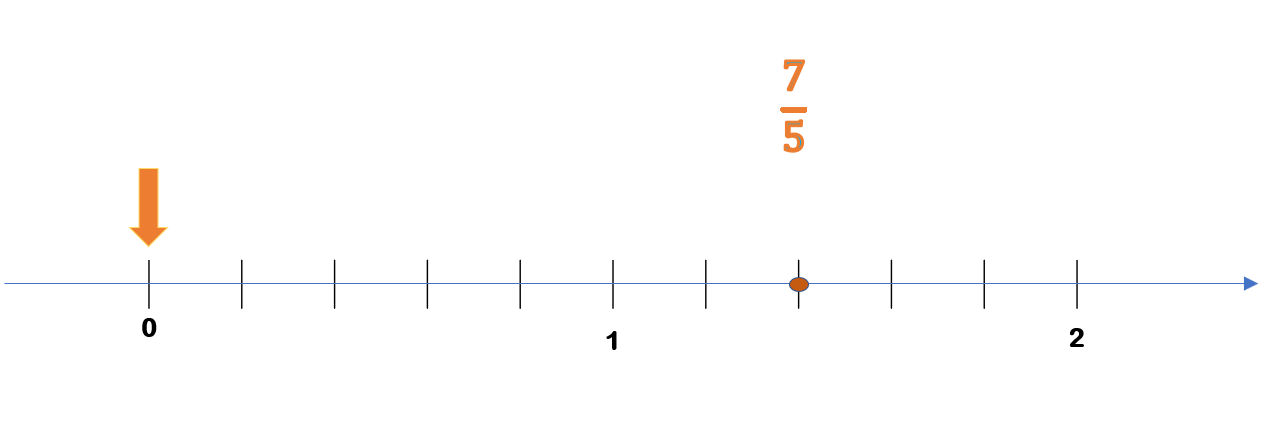
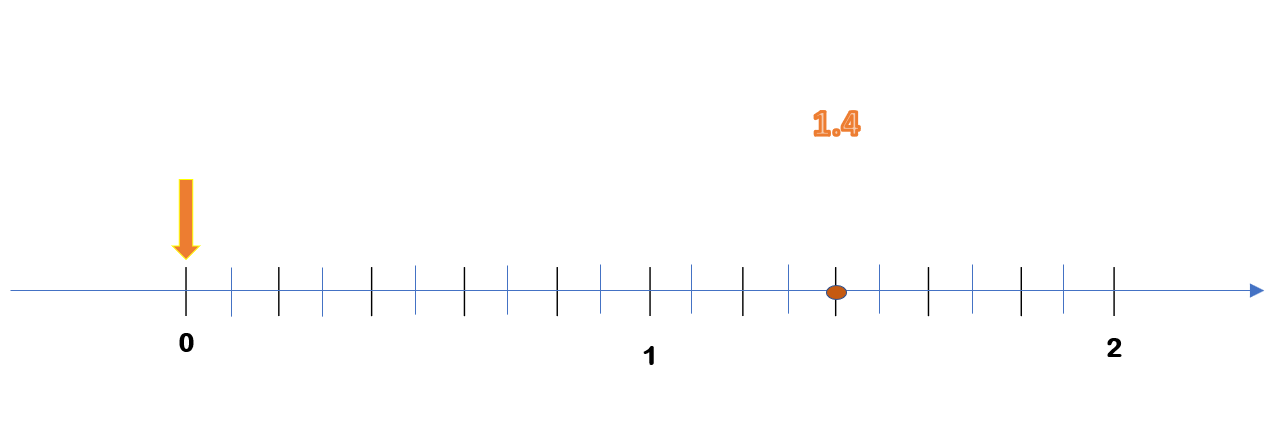
Su equivalente en número decimal es 1.4
Para ubicar este número decimal, puedes dividir los dos primeros enteros en diez partes iguales, tomar el primer entero completo y las siguientes cuatro partes del segundo entero, como se muestra a continuación:
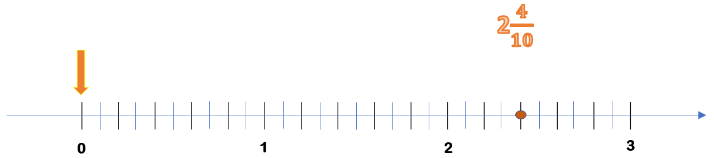
Trata de resolver cómo ubicar en la recta numérica el número 2.4. Puedes hacerlo de la siguiente manera: divide los tres primeros enteros en 10 partes iguales y toma dos enteros y 4 divisiones del siguiente. Como se muestra a continuación:

Resuelto lo anterior, ¿cuál es la fracción equivalente a este número decimal?
La fracción es 2 enteros 4/10, es un número mixto por tener una parte entera y una fracción.
¿Qué fracciones podrías encontrar entre el cero y 4/3?

Una estrategia que puedes emplear es: dividir a la mitad cada una de las partes obtenidas y de este modo tendrás enteros divididos en sextos, así puedes señalar cualquier fracción que anteceda a 4/3. Por ejemplo: 4/6 o 7/6, observa:

No sólo puedes dividir por la mitad a cada fracción obtenida. Por ejemplo, puedes dividir en cuatro cada fracción y así obtener doceavos. Lo que significa que puedes encontrar fracciones menores a 4/6 o que se encuentren entre las que ya has identificado.
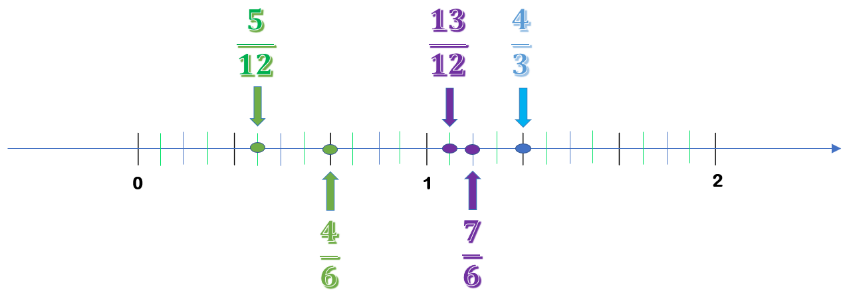
Este proceso lo puedes repetir una cantidad infinita de ocasiones, esa es una de las propiedades de los números racionales, que incluye tanto a los decimales como a los fraccionarios: La densidad y con esta propiedad puedes ubicar una cantidad infinita de números.
Hay muchos lugares en donde puedes ordenar según su valor: tanto decimales como fracciones. En este caso enfócate en la música. La música fascina a muchas personas, ¿Sabías que está estrechamente ligada con las matemáticas?, cada pieza musical que existe en el mundo está compuesta por una combinación de notas musicales y ritmos en el tiempo, con la combinación de éstas se crean infinidad de melodías. Éstas se agrupan en unidades métricas llamadas: compases. Pon atención en la siguiente melodía:
GAVOTA
Existen diferentes tipos de compases, y en esta ocasión te concentrarás en el más común de todos: 4/4, es decir un compás de 4 tiempos. Analiza algunos ritmos:
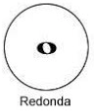
La redonda, la cual tiene una duración de 4 tiempos, por lo que en un compás de 4/4 representaría un entero.
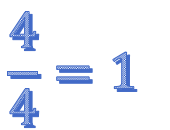
Reconocerás los ritmos por medio del Violonchelo. Y para que hagas este análisis más interactivo, trata de imitar el instrumento con tu voz o de llevar el ritmo con tus manos o con algún objeto que pueda emitir un sonido.
PRESENTACIÓN

REDONDA
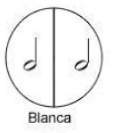
Conoce a la blanca, que dura un total de 2 tiempos, así que es la mitad del tiempo de una redonda, por lo que la representamos con la fracción ½. Toma tu cuaderno de apuntes, traza una recta numérica y ubica ½.


Escúchala y no olvides marcar el ritmo con tu voz o golpeando suavemente las palmas de tus manos en tus piernas.
BLANCA
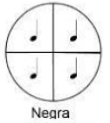
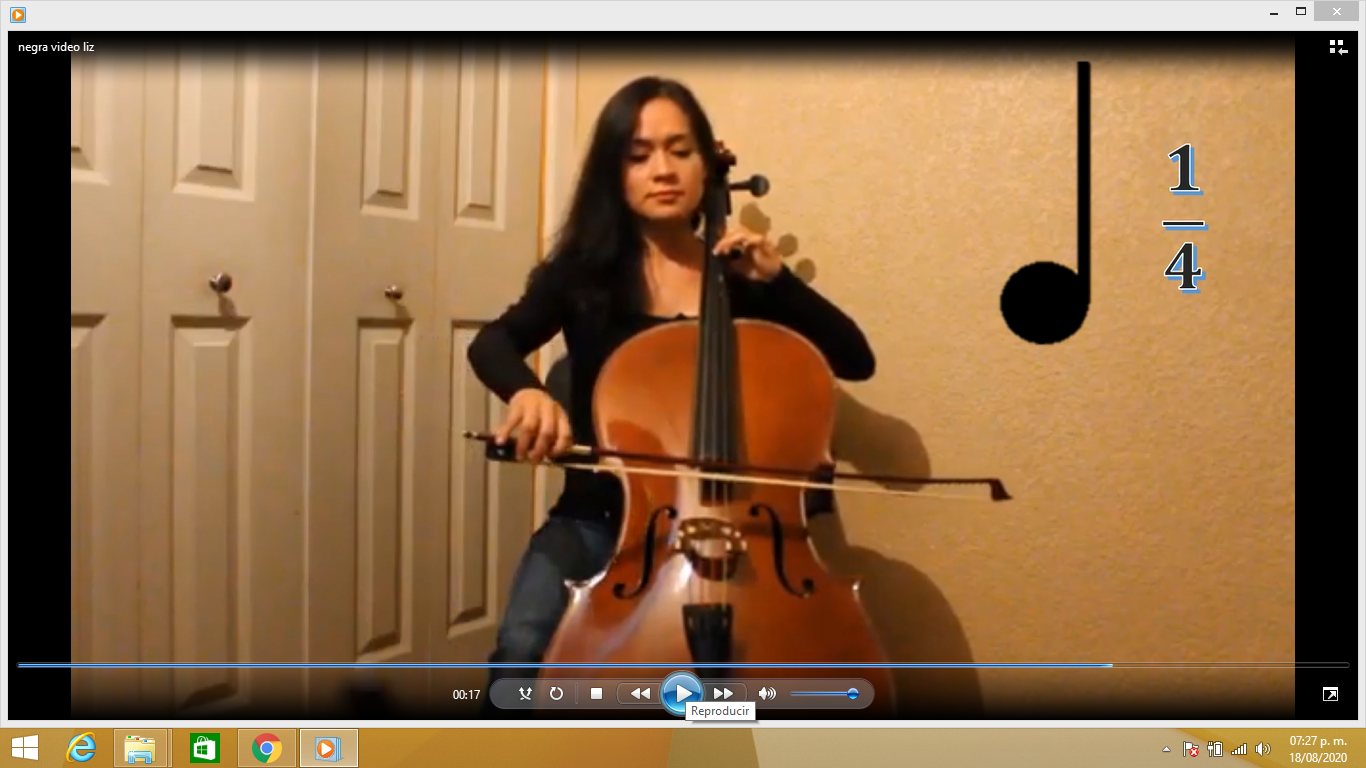
El siguiente ritmo, corresponde a la negra
¿Sabes que su valor es la mitad de una blanca? Una negra dura sólo 1 tiempo, y es la cuarta parte de una redonda, por lo que la puedes representar con la fracción ¼. En tu cuaderno ubica esta fracción usando la misma recta numérica del ejercicio anterior.


Para saber cómo sonaría en el violonchelo, observa el siguiente video:
NEGRA
Conozce el penúltimo ritmo de este ejercicio: la corchea.
Es la mitad del tiempo de una negra, lo que quiere decir que es 1/8 del tiempo de una redonda. Haciendo uso de tu misma recta, ubica la fracción ⅛.



Para escuchar la corchea, en el Violonchelo, observa el siguiente video:
CORCHEA

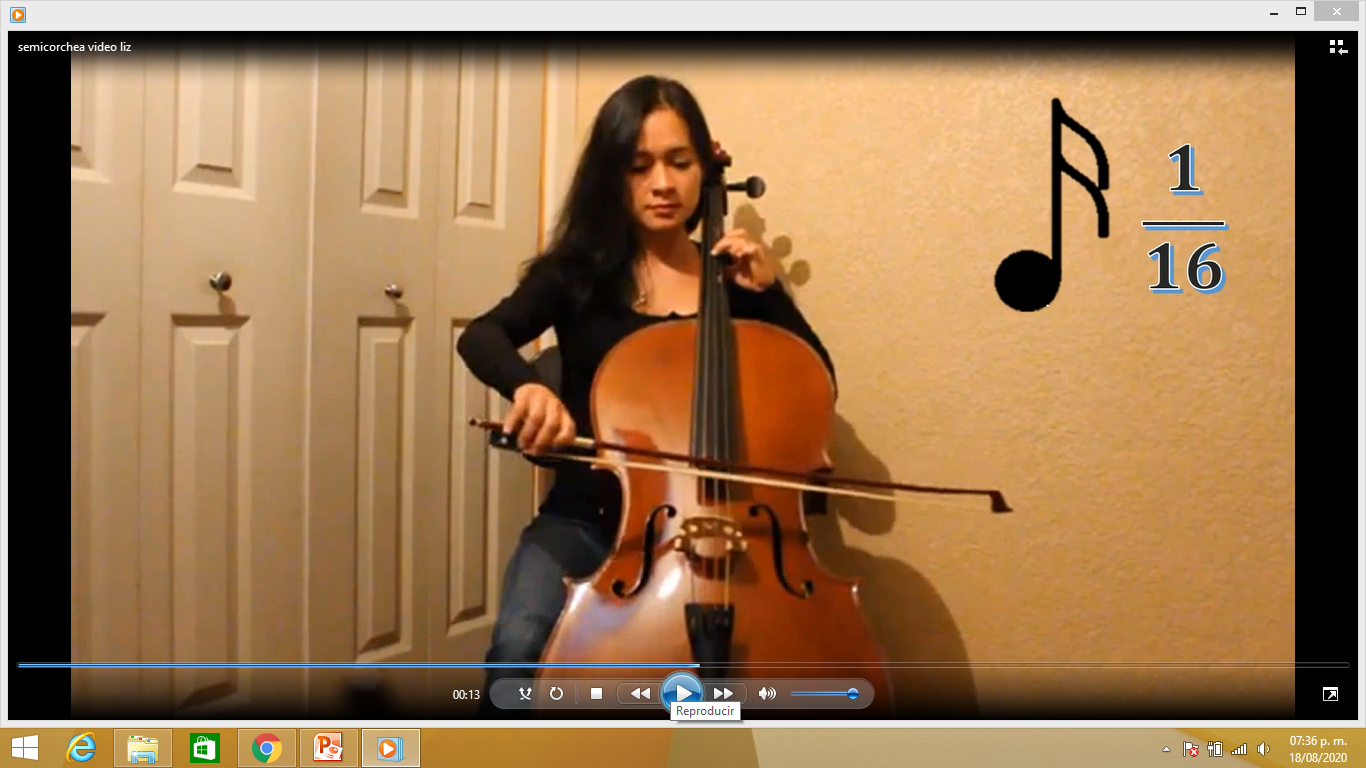
Por último, analiza la semicorchea. Representada con la fracción 1/16, es la mitad de una corchea y 1 dieciseisava parte de la redonda. En la misma recta, marca la fracción 1/16.



SEMICORCHEA
Observa cada una de las fracciones anteriores, en la recta numérica.

Entre más pequeñas son las partes en las que dividiste, menor es la fracción; si es que toma sólo una de esas partes.
¿Qué compás resultaría con dos blancas y una negra?


Un compás de 5/4.
Y ¿Cómo ubicas la fracción 5/4 en la recta numérica?, ¿cómo se representa dicha fracción en números decimales?
Como 1.25 y se ubica en la recta numérica de la siguiente manera:
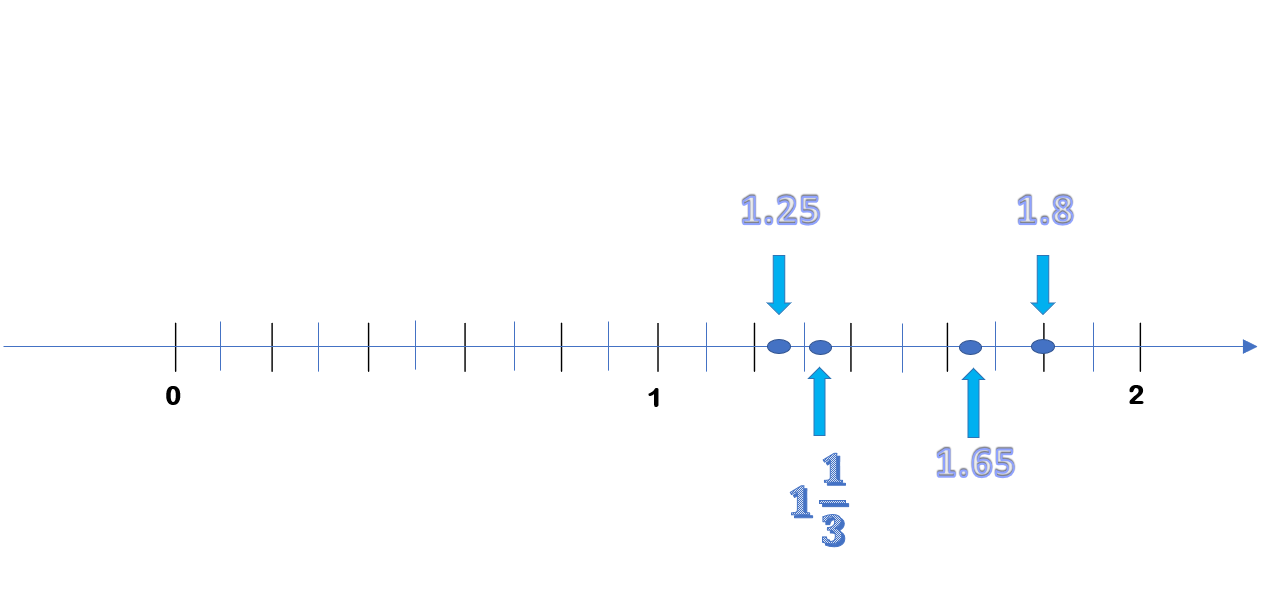
El número 1.8, es mayor o menor que el 1.25 y el número 1.65 es menor que el 1.8.
¿A cuántas negras equivalen 2 blancas?
Siguiendo con el ejemplo anterior, toma tu cuaderno, lápiz y realiza la siguiente actividad:
- ¿Qué dura más? Si tienes cuatro semicorcheas y una blanca, o tres negras.
- Si tienes dos negras y seis corcheas, o una redonda y una corchea
- Si tienes dos blancas y cuatro corcheas, u ocho semicorcheas y dos negras
- O bien, si tienes dos blancas y dos semicorcheas, o una redonda y tres negras
- Por último: dos blancas y tres negras, o cinco semicorcheas y tres corcheas.
Una opción, para conocer las respuestas, es obtener equivalencias de los tiempos, por ejemplo: dos semicorcheas son igual a una corchea, dos corcheas son igual a una negra y una blanca equivale a dos negras, y equivalen a un total de 3 negras. Quiere decir, lo mismo que el segundo caso, y en fracción es igual a ¾, en ambas situaciones.

Existen diferentes formas por las cuales puedes llegar al resultado. Analiza otra forma de resolverlo.
La estrategia será utilizar la recta numérica, observa que la recta está dividida en 8 partes, ya que la fracción menor es la corchea de ⅛. Así la localizas más rápido. Ahora recuerda que la negra equivale a dos corcheas, por lo tanto, ocupan dos espacios de ⅛. Así llegas hasta tener un entero y 2 octavos que equivale a 1.25, y en comparación tenemos una redonda que equivale a un entero y una corchea ⅛ que en decimal sería 1.125.
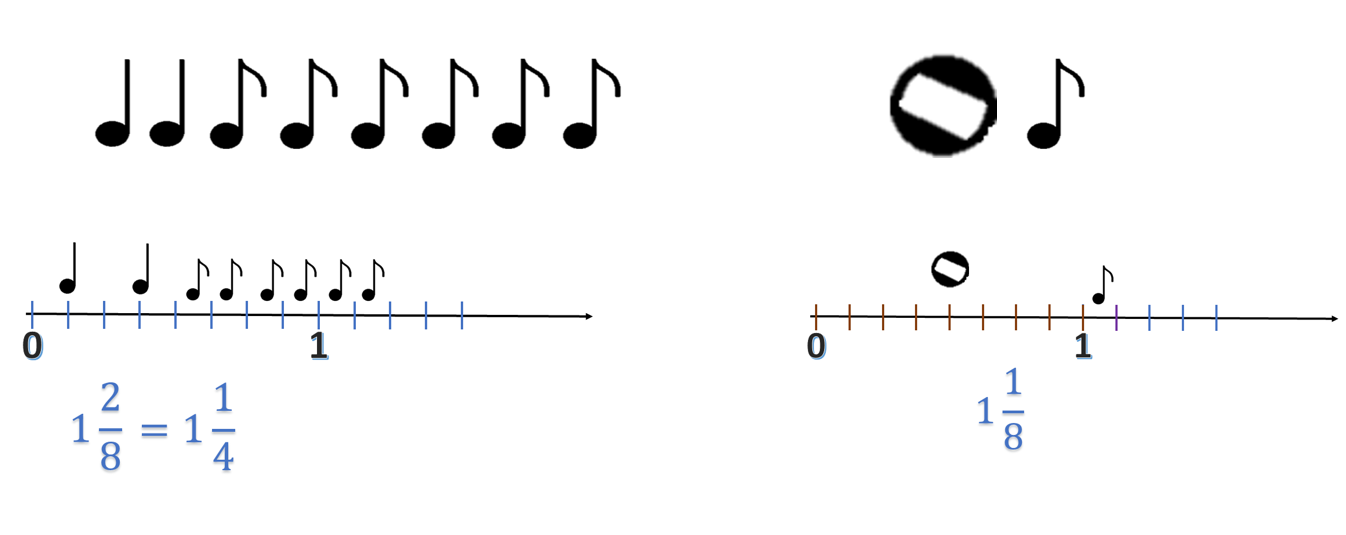
También es muy útil la recta numérica para encontrar estas comparaciones y conocer cuál es mayor.
¿Obtuviste el mismo resultado?, ¿utilizaste la recta numérica o la equivalencia entre los tiempos? Ahora, analiza lo siguiente:
Observaste el tiempo de cada uno con su representación gráfica. Si ahora usas áreas, al tener dos blancas tienes dos mitades del círculo por ser ½, y cada corchea tiene la octava parte del círculo. Al tener cuatro obtienes la mitad de un círculo completo, por lo tanto, es: un entero un medio o 1.5. Otro ejemplo: la semicorchea tiene 1/16 del círculo completo y al tener 8 juntamos la mitad de un círculo, a su vez cada negra es un 1/4 y al tener dos, completamos medio círculo; al unir las dos mitades obtenemos un entero, por lo tanto, este es menor.

Hay formas de resolver este tipo de problemas, veamos otra forma, y que es muy sencilla. Probablemente ya sabes cuál es y has utilizado esta estrategia. Observa la siguiente imagen:
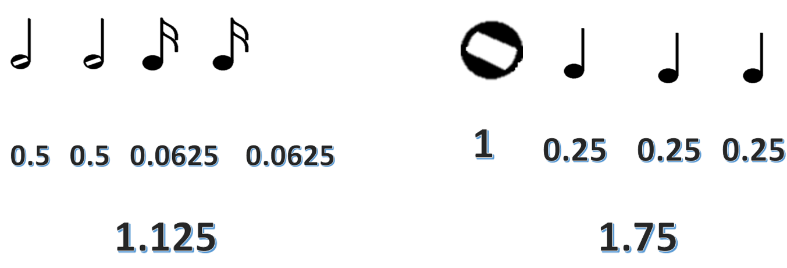
Cada blanca representa ½ por lo que en decimales es 0.5, a su vez cada semicorchea al ser 1/16 su representación decimal es 0.0625. Por lo tanto, de las dos blancas y las dos negras tenemos 1.125. Ahora la redonda, al ser el tiempo completo equivale al entero; por otro lado, cada negra representa ¼, su representación decimal sería 0.25 y tenemos 3, por lo que al tener una redonda y tres negras obtienes 1.75, que resulta ser más grande que 1.125.
Recuerda que, para obtener la representación decimal de una fracción, únicamente se divide el numerador entre el denominador.
La representación mayor en tiempo fue:
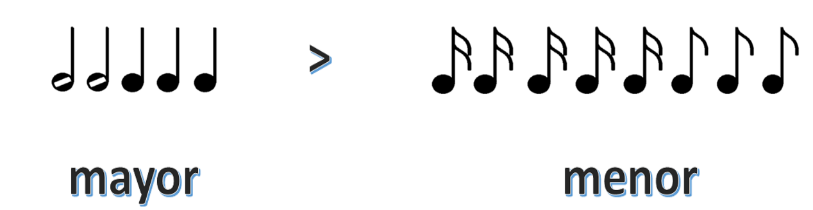
Dos blancas y tres negras representan mayor tiempo que: cinco semicorcheas y dos corcheas.
La próxima vez que escuches tu canción favorita, recuerda la bella relación que tiene con las matemáticas y sigue el ritmo.
Si tienes dudas, recuerda que puedes revisar en tu libro de texto el tema y realizar las actividades que ahí te sugieren.
El reto de hoy:
¿Sabes que hay unas llaves que reciben el nombre de llave española?

Estas llaves se miden con fracciones. Como ½, 5/16 o ⅞.
Primero copia, en tu cuaderno, las medidas de las siguientes llaves españolas: Cinco octavos, un medio, nueve dieciseisavos y tres cuartos.
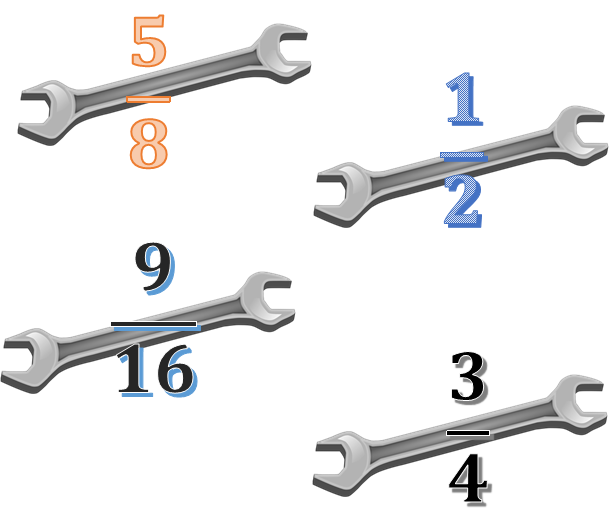
El reto consiste en que sin ver las llaves físicamente, las organices de menor a mayor únicamente conociendo su medida en fracción. ¿Qué estrategia puedes seguir?, ¿puedes auxiliarte de una recta numérica?, ¿en qué número debes centrar tu atención en primer lugar: numerador o denominador?, ¿posteriormente, qué debes hacer?
Esto nos recuerda que las fracciones están presentes en todo lugar. Por ejemplo, ¿sabías que existen diferentes tipos de hojas de papel y que se pueden clasificar por su gramaje? El gramaje se refiere al peso que tiene la hoja de un tamaño en específico.
Toma nota y encuentres la solución.
En un lugar de venta de papel se tienen los siguientes gramajes:
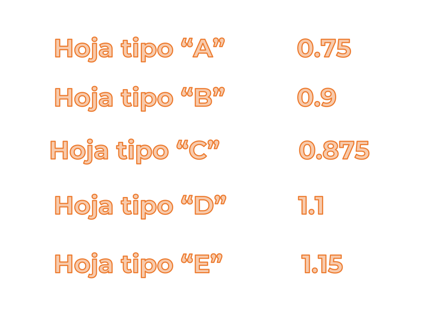
Si tuvieras que ordenar las hojas de menor a mayor, de acuerdo con su gramaje: ¿En qué orden las acomodarías? ¿Qué estrategia seguirías?
Realiza otro reto: En casa intenta crear un ritmo, verás lo divertido que es.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
