Variación directa

Variación directa

Aprendizaje esperado: calcula valores faltantes en problemas de proporcionalidad directa, con constante natural, fracción o decimal (incluyendo tablas de variación).

Énfasis: usar tablas de variación para resolver problemas de variación directa e identificar cuando haya variación directa o no.

¿Qué vamos a aprender?

Continuaremos con tema anterior, en donde resolviste diversas situaciones que involucraron a la proporcionalidad directa. Analizarás un problema, desde la concentración de los datos de éste, en una tabla; para determinar cuándo hay variación proporcional directa y cuándo no.

¿Qué hacemos?

Probablemente durante este periodo de contingencia, has estado ayudando en tu hogar con algunas labores. A continuación, plantearemos un problema con una de las tareas del hogar: la cocina.

Vamos a preparar un pay, para ello tenemos un recetario, en él se mencionan los ingredientes necesarios para hacer un pay para 10 personas; sin embargo, sólo hay 5 personas en el hogar.

¿Qué debemos hacer con esa lista de ingredientes para preparar un pay sólo para 5 personas?

Para eso, observa el siguiente video del minuto: 0:24 a 01:44 con una situación similar.

• Diferentes mezclas

https://www.youtube.com/watch?v=DYlP7b8v6c0&feature=youtu.be

Como notaste, es necesario conservar la relación entre la cantidad de cada ingrediente que se va a utilizar y el número de porciones, o personas, para las cuales está contemplada la receta, pero si el número de porciones o personas es diferente, será necesario ajustar la cantidad de cada ingrediente, de manera que se mantenga la misma proporción que en la receta original.

Regresando al problema inicial, tendríamos que ajustar en la misma proporción, en este caso, es a la mitad. Pero ¿qué significa conservar la proporción entre las cantidades?, ¿cómo se identifica?

Para dar respuesta a estas preguntas, te proponemos analizar algunas situaciones similares a la anterior, que están presentes en nuestro contexto.

Iniciaremos planteando una situación que ocurre cada inicio de ciclo escolar. Siempre acudes a las papelerías a comprar los materiales que utilizarás en la escuela. ¿Cierto?

Pues, en la papelería “El lapicito”, se encuentra la siguiente tabla de precios:

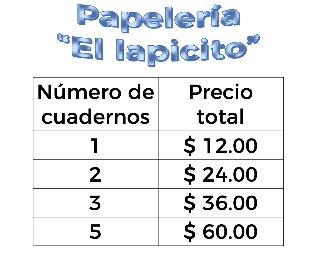
En esta tabla puedes darte cuenta de que al comprar un cuaderno se pagan 12 pesos, por dos cuadernos se pagan 24 pesos, por tres cuadernos se pagan 36 pesos y por cinco cuadernos, 60 pesos. Lo que significa que la tabla permite establecer la relación entre la cantidad de cuadernos y su precio en pesos.

Determinemos si existe una variación directamente proporcional entre estas cantidades.

La variación directamente proporcional indica que al aumentar o disminuir una de las dos magnitudes, la otra también aumenta o disminuye en la misma proporción.

En dicha tabla, la primera magnitud corresponde a la cantidad de cuadernos y la segunda magnitud corresponde a su precio en pesos. Por lo tanto, podemos establecer una relación entre ambas magnitudes de nuestra tabla para determinar si su comportamiento presenta una variación proporcional directa o no. Es decir: si la cantidad de cuadernos aumenta, el precio debe aumentar en la misma proporción.

Entonces, veamos qué relación encontramos al dividir el precio total de los cuadernos, entre el número de cuadernos.

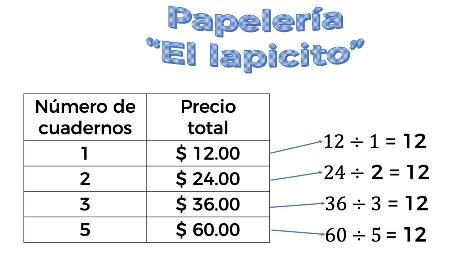
Recuerda que la razón es la relación entre dos cantidades, y que pueden ser de la misma naturaleza o no. En este caso, no son de la misma naturaleza. Observa que al obtener los cocientes 12 entre 1, 24 entre 2, 36 entre 3, y 60 entre 5. Se obtiene el mismo número, en este caso 12. Por lo tanto, al relacionar ambas magnitudes de la tabla obtenemos el mismo cociente.

Esto se interpreta como: si compras dos cuadernos el precio se duplica, es decir se pagan 24 pesos, si compras tres cuadernos, el precio se triplicará con respecto al costo de un cuaderno, y así sucesivamente. Entonces, en esta tabla hay una variación directamente proporcional, porque el precio aumenta de manera directamente proporcional al número de cuadernos que se compran.

En los ejemplos anteriores, observaste que los datos de las situaciones planteadas se organizaron en tablas para realizar una comparación entre ellos, esto permitió generar un análisis para determinar si existe una variación directamente proporcional. Es decir, si una cantidad aumenta la otra también aumentará en la misma proporción.

Entonces, si en una tabla hay dos magnitudes relacionadas entre sí, y una de ellas aumenta y la otra también aumenta en la misma proporción, ¿podemos afirmar que, se establece una variación directamente proporcional? Para responder a esta pregunta analiza la siguiente situación:

Los alumnos de una escuela comentaron que el día del Amor y la Amistad, en el mercado de plantas, encontraron un comercio en donde se venden ramos de flores, y los costos de estos tienen variaciones. En la siguiente tabla se muestran las cantidades.

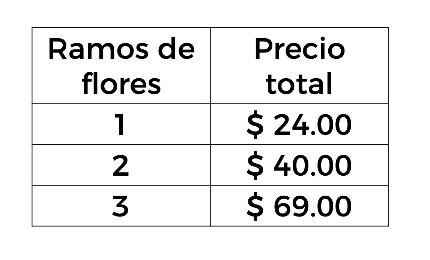
Con estos datos, ¿se podrá afirmar que existe una variación directamente proporcional entre el número de ramos que se compran con su precio?

Así como lo hiciste anteriormente, establece una relación entre el número de ramos y su precio correspondiente, para determinar si en su comportamiento hay una variación directamente proporcional o no. Es decir, para que esto ocurra, si la cantidad de ramos aumenta, el precio también debe aumentar en la misma proporción.

Veamos qué relación encontramos al dividir el precio total de los ramos entre el número de ramos.

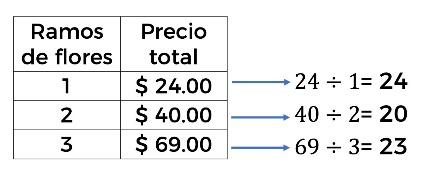
Observa que al obtener los cocientes: 24 entre 1, 40 entre 2 y 69 entre 3, se obtienen los resultados 24, 20 y 23 respectivamente, los cuales son diferentes. Entonces, al relacionar ambas cantidades en la tabla no obtenemos el mismo cociente, lo que nos indica que no hay una constante de proporcionalidad.

En consecuencia, no es proporcional el número de ramos con el precio total que oferta el vendedor, con esto establecemos que ambas cantidades aumentan, pero, no hay una variación directamente proporcional. Para que haya una variación directamente proporcional, al comprar el doble de ramos se debería pagar el doble de su precio, es decir $48; pero en este caso no sucede así, ya que la florería vende dos ramos en $40.

Al hacer una oferta y disminuir el costo de los ramos, por mayoreo, eso rompe con la proporcionalidad, ¿te diste cuenta?

Esto sucede, para esta situación, porque la mayoría de los comerciantes en nuestro país, para atraer a clientes y vender más, ofertan sus productos a un menor precio dependiendo de la cantidad de productos adquiridos. Es decir, hacen una disminución en el precio final por la compra de mayor volumen del mismo producto.

En los ejemplos anteriores realizamos la comparación de datos concentrados en registros tabulares o tablas de datos. Esto es un buen apoyo para organizar datos y con ello resolver problemas que se presentan en nuestro contexto.

Utilizaremos otra situación, para señalar la importancia del uso de las tablas de datos, en estos procedimientos. Por ejemplo: Imagina que quieres comprar una motocicleta para recorrer algunos de los hermosos paisajes que tiene nuestro país. En días pasados encontraste algunas ofertas en internet, sobre el precio de un par de motocicletas, así como la información de su rendimiento.

En las siguientes tablas se muestra la información de cada una de las motocicletas.

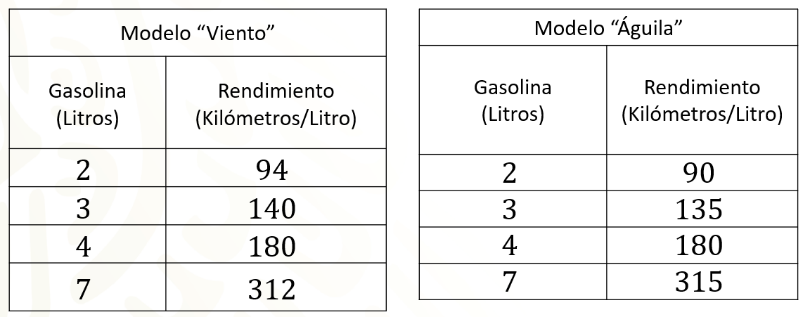
¿Cuál motocicleta comprarías y por qué?

Para ello, determinemos las características de los datos que se han registrado en cada tabla, ya que esto nos puede ayudar a determinar cuál de las dos comprar.

De acuerdo con los datos en la tabla del modelo “Viento”, las dos magnitudes aumentan, tanto los litros como los kilómetros, pero ¿su variación será directamente proporcional? Es decir, ¿hay una relación de proporcionalidad entre la cantidad de litros de gasolina con la cantidad de kilómetros que se pueden recorrer?

En este caso, también, podemos establecer una relación entre ambas magnitudes de nuestra tabla, para determinar si su comportamiento es o no una variación directamente proporcional. Es decir, si los litros de gasolina aumentan, el rendimiento en kilómetros debe aumentar en la misma proporción.

Veamos qué relación encontramos al dividir la magnitud que corresponde al rendimiento en kilómetros entre la magnitud que corresponde a los litros de gasolina.

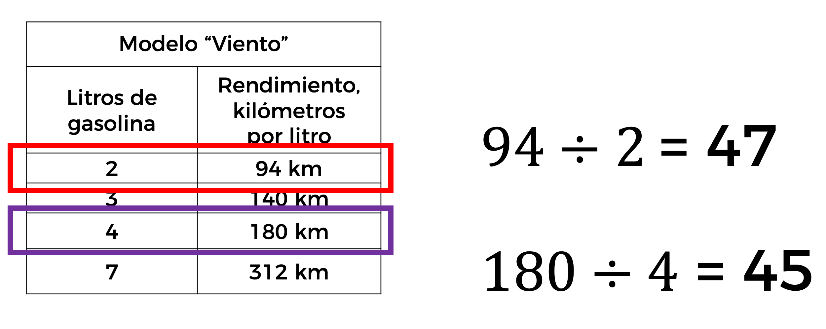
Analizando las razones internas para determinar si hay proporcionalidad directa, observamos que 4 es el doble de 2, pero 180 no es el doble de 94, por lo que la variación no es de proporcionalidad directa, ya que, aunque ambas cantidades aumentan, no lo hacen en la misma proporción.

Ahora analicemos la segunda tabla. Verifiquemos en términos operativos la correspondencia entre los valores de rendimiento con los litros de gasolina. ¿Sucederá lo mismo que con los datos de la tabla anterior?

Ahora, observamos que el rendimiento fue el mismo, el cual corresponde a la constante de proporcionalidad.

Después de realizar el planteamiento anterior, ¿será la única forma de comprobar que, en una tabla, donde se concentran los datos de un problema, existe una variación directamente proporcional?

Para responder a la pregunta, te proponemos realizar un análisis siguiendo otro camino.

Del modelo “Águila”, sabemos que con 7 litros de gasolina podemos recorrer 315 km.

¿Obtendremos la misma distancia recorrida si sumamos el recorrido de 3 litros con el recorrido de 4 litros de gasolina?

Comparemos sumando término a término, esto consiste en sumar 3 más 4 litros de gasolina y 135 más 180 kilómetros, el primer resultado nos da 7 litros y el segundo 315 km.

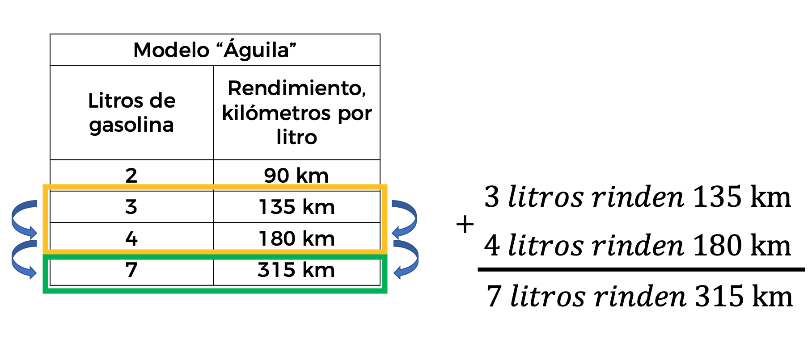
Con esta comparación nos damos cuenta de que es una variación directamente proporcional, puesto que la equivalencia de ambas sumas corresponde al rendimiento por 7 litros.

Utilizando la información que hemos analizado, concluimos que es conveniente comprar el modelo “Águila”, porque podemos recorrer los mismos kilómetros por cada litro de gasolina y a su vez, esto nos permite saber, con certeza, el gasto de combustible en distancias determinadas.

Ahora supongamos que no conocemos la constante de proporcionalidad, pero que sabemos que la distancia que recorre la motocicleta es directamente proporcional a los litros que consume, a partir de esto, podemos obtener el rendimiento para cualquier cantidad de litros de gasolina. Por ejemplo, calculemos el rendimiento para 5 litros.

Como ya sabemos, tanto los litros como la distancia recorrida en km, aumentan en la misma proporción, existiendo una variación directamente proporcional. Partiendo de la información anterior, usamos las razones internas:

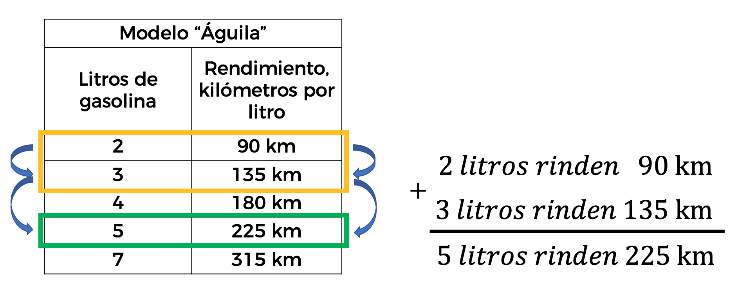
De esta forma hemos determinado otra manera de comprobar si en los datos concentrados en una tabla existe una variación directa, sumando término a término dos datos de la misma magnitud y sus dos correspondientes, pero recuerda que este procedimiento podrá efectuarse cuando hay relación entre los valores involucrados.

Hasta este momento has analizado tres situaciones, a partir de organizar los datos en una tabla, identificaste si hay o no variación directamente proporcional, esto te ha ayudado a resolver situaciones particulares; como fue el caso de las motocicletas.

La proporcionalidad directa, es una gran guía. Realicemos otra actividad:

Un joven fue de visita con su abuelo y lo encontró reparando una cerca de su parcela, el abuelo lo mandó a comprar 80 metros de alambre de púas, por lo que acudió a la tienda de materiales en donde había una tabla que mostraba el costo para diferentes cantidades de alambre, pero que no incluía el costo de 80 metros:

¿Cómo podríamos calcular el costo por los 80 metros?

En un primer momento, al observar la tabla nos damos cuenta de que tanto los metros como el precio aumentan, ahora verifiquemos si su variación es directamente proporcional:

Aplicando lo que has aprendido anteriormente, se puede comprobar de dos maneras:

• obteniendo el cociente de las magnitudes correspondientes para verificar si existe una constante de proporcionalidad.
• O, realizando la suma de término a término.

Hagamos el procedimiento con los cocientes de las magnitudes para determinar la constante de proporcionalidad:

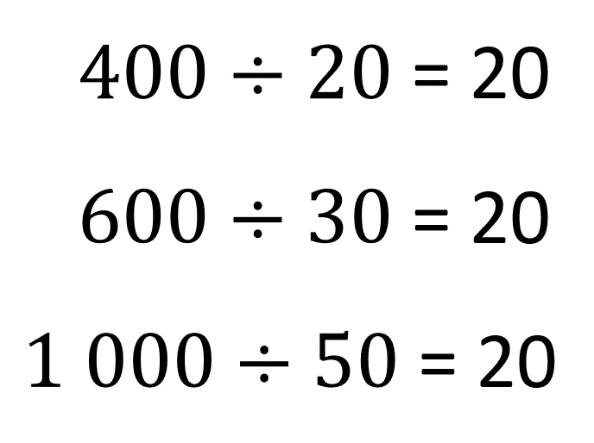
Los cocientes que se encontraron son los mismos, por lo que sí hay una constante de proporcionalidad, en este caso 20.

De tal modo que ahora podemos determinar este costo al encontrar el producto de 80 por la constante de proporcionalidad:

Analicemos qué otra característica podemos encontrar en los datos concentrados en la tabla anterior; para ello tomemos dos parejas de datos, y sus correspondientes, para comprobar que son equivalentes se multiplica de la siguiente manera:

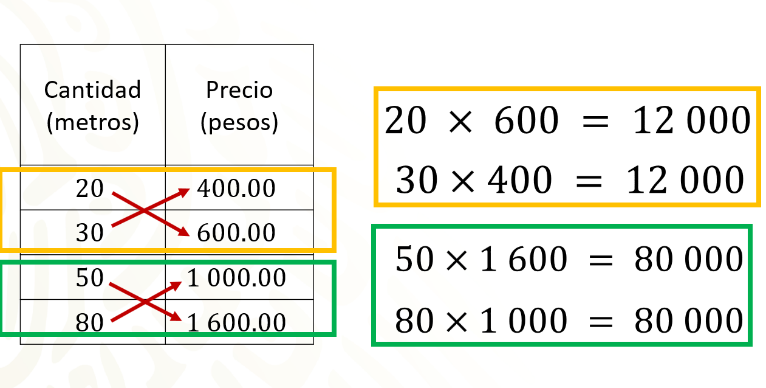
¿Te diste cuenta de que, al multiplicar las magnitudes correspondientes de manera cruzada, el producto es el mismo en cada pareja de datos?

Si sucede lo anterior, tendremos un elemento más para afirmar que los datos que se encuentran en la tabla son proporcionales, ya que mantienen una relación de variación directamente proporcional.

Con base en la afirmación anterior, ¿se podría considerar cualquier pareja de magnitudes para comprobar si tenemos o no una relación de variación directamente proporcional?

Para ello, realicemos la comprobación de dicha afirmación, tomando cualquier pareja de datos de la tabla.

En esta tabla, estamos relacionando 4 cantidades. Al obtener productos iguales, se observa que una de las magnitudes cambia y la otra también se modifica en la misma proporción. Esto quiere decir que cuando las razones de una variación directa son equivalentes al multiplicar de manera cruzada, los productos deben ser iguales para poder afirmar que existe una variación directamente proporcional.

De acuerdo con todo lo que viste en esta lección podemos concluir que:

Existe una relación de variación directamente proporcional cuando dos cantidades se relacionan de tal manera que, si una aumenta o se reduce, la otra también lo hace en la misma proporción; por ejemplo, si una se duplica o se triplica, la otra también, y si una se reduce a la mitad o a la tercera parte, sucede lo mismo con la otra.

Los valores de ambas magnitudes tienen una relación constante que llamamos: constante de proporcionalidad.

Así mismo, lograste identificar tres formas de determinar si hay o no variación directamente proporcional en los datos concentrados en una tabla:

• Calculando la constante de proporcionalidad.
• Usando las razones internas.
• Y por medio de razones equivalentes.

Te invitamos a buscar en tu libro de texto el aprendizaje esperado que has estado trabajando en esta lección; en el libro podrás identificar la siguiente información:

Lo que has aprendido en esta lección, puedes aplicarlo en muchos casos, por ejemplo, para calcular lo que deben cobrar los empleados de una empresa por un número de días trabajados o por un determinado número de horas de trabajo.

Analicemos la información que se presenta en la siguiente tabla, donde se muestran los días trabajados de un empleado de una empresa equis, y su salario correspondiente, sabiendo que el pago por día de trabajo siempre es el mismo.

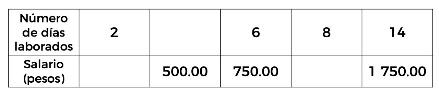
Observa que en la primera fila tenemos los días laborados, que son 2, 6, 8 y 14 días respectivamente. Mientras que en la segunda fila tenemos el salario, en pesos mexicanos, por día de trabajo. Basándonos en la información anterior, ¿qué debemos hacer para ayudar al empleado a determinar cuánto debe cobrar por 8 días de trabajo?

Para encontrar la constante de proporcionalidad, podemos dividir 750 entre 6 o 1750 entre 14, como hay una relación de proporcionalidad directa, sabemos que en ambas divisiones se obtiene el mismo valor, como puedes ver:

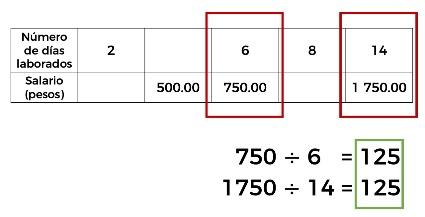
Ya que se obtiene una constante de proporcionalidad, la cual nos indica que por cada día laborado, el empleado cobra 125 pesos. Utilicemos dicha constante para dar respuesta al planteamiento anterior y calculemos el producto de 125 por los 8 días trabajados.

El reto de hoy:

En esta tabla aún falta determinar ¿Cuánto debe cobrar el empleado por 2 días trabajados? Y, si le pagan $500, ¿cuántos días trabajó?

Te retamos a encontrar estos valores faltantes, utilizando cualquiera de las formas o procedimientos que estudiaste en esta lección: El uso de razones, internas, la constante de proporcionalidad o mediante razones equivalentes.

También puedes pedir ayuda y retroalimentación a distancia de tus maestras o maestros cuando sea posible.

¡Buen trabajo!

Gracias por tu esfuerzo.