En busca del mejor valor
Aprendizaje esperado: uso de la media (promedio), la mediana y la moda en la resolución de problemas.
Énfasis: analiza la conveniencia de señalar la media aritmética, la mediana o la moda como cantidad representativa de un conjunto de datos..
¿Qué vamos a aprender?
En esta sesión vas a emplear la media (promedio), la mediana y la moda en la resolución de problemas, así también analizarás la conveniencia de usar la media aritmética, la mediana o la moda, como cantidad representativa de un conjunto de datos.
Vas a necesitar tu libro Desafíos Sexto grado, tu cuaderno u hoja para tomar notas, lápiz, goma, sacapuntas y mucha disposición.
¿Qué hacemos?
Recuerda que en el desafío 52 y 53 se calculó el promedio de edad de un grupo de personas. Se ordenaron los datos de mayor a menor para encontrar la mediana y también localizaste el dato que más se repetía.
Es muy importante que apliques muy bien los conceptos aprendidos para obtener las medidas de tendencia central, pero ten presente que siempre debes analizar las situaciones para determinar lo que más convenga en el uso de dichos valores, por ejemplo, sabes que las vacunas ya se están calendarizando por grupos de edad.
En varios lugares de nuestro país ya llegaron o están a punto de llegar las vacunas que van a prevenir daños graves en la salud causados por el COVID-19
Actividad 1
Revisa muy bien el siguiente ejemplo para que puedas obtener las respuestas.
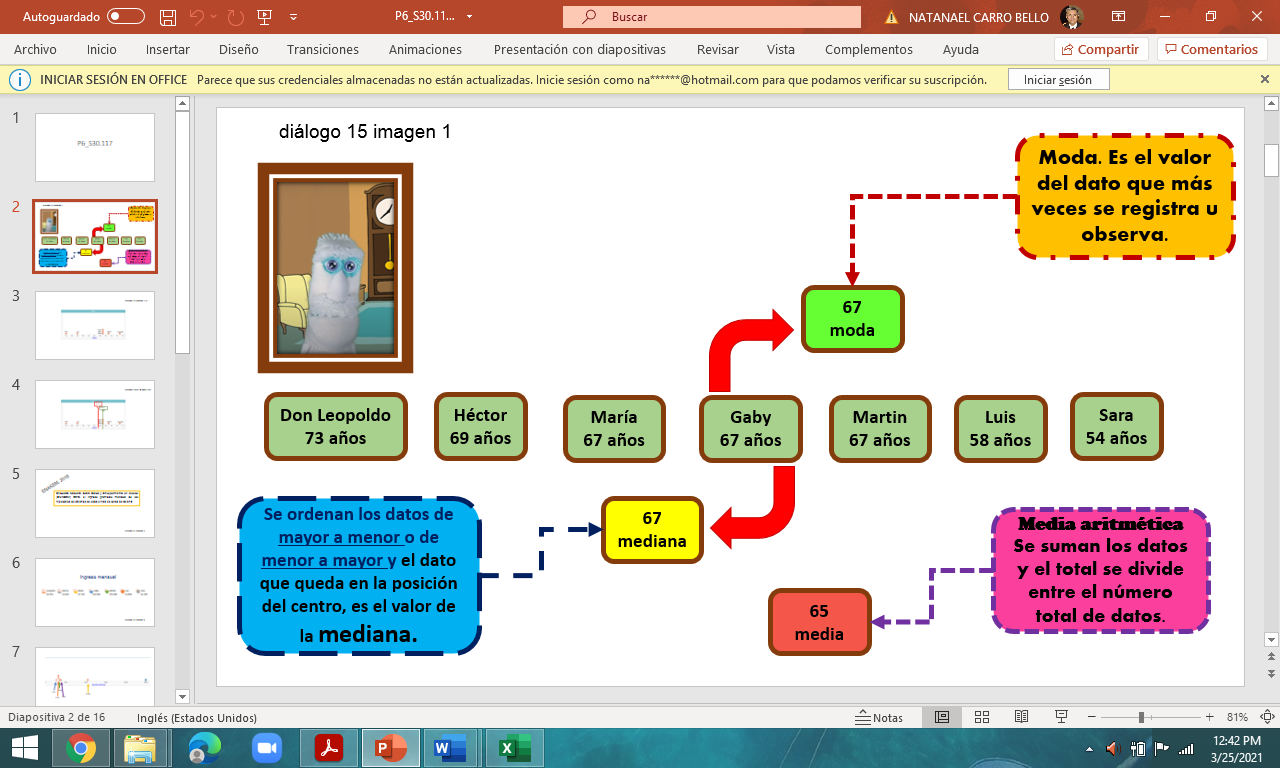
Cupertino calculó que el promedio de edad de don Leopoldo y sus hermanos era de 65 años, también obtuvo que la mediana de las edades era 67 años y la edad más frecuente o moda también fue 67
De acuerdo con los datos que calculó Cupertino, ¿Crees conveniente usar alguna de ellas para afirmar que Don Leopoldo y sus hermanos ya van a ser vacunados?
Por ejemplo, es correcto decir que, dado que la edad promedio de Don Leopoldo y sus hermanos es 65 años, los siete hermanos ya serán vacunados.
Observa, 60 años es el grupo de edad de las personas que pueden ya ser vacunadas, pero, ¿Los siete hermanos tienen 60 años o más?
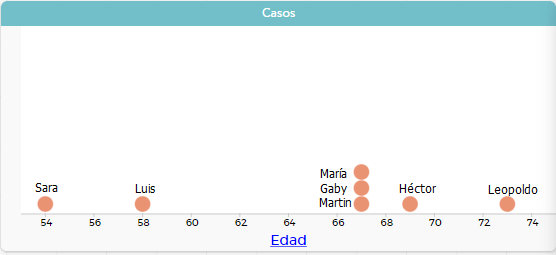
No, Luis y Sara son menores de 60 años.
En este caso, no conviene usar como referente ninguna de las tres medidas, ni media aritmética, ni moda, ni mediana.
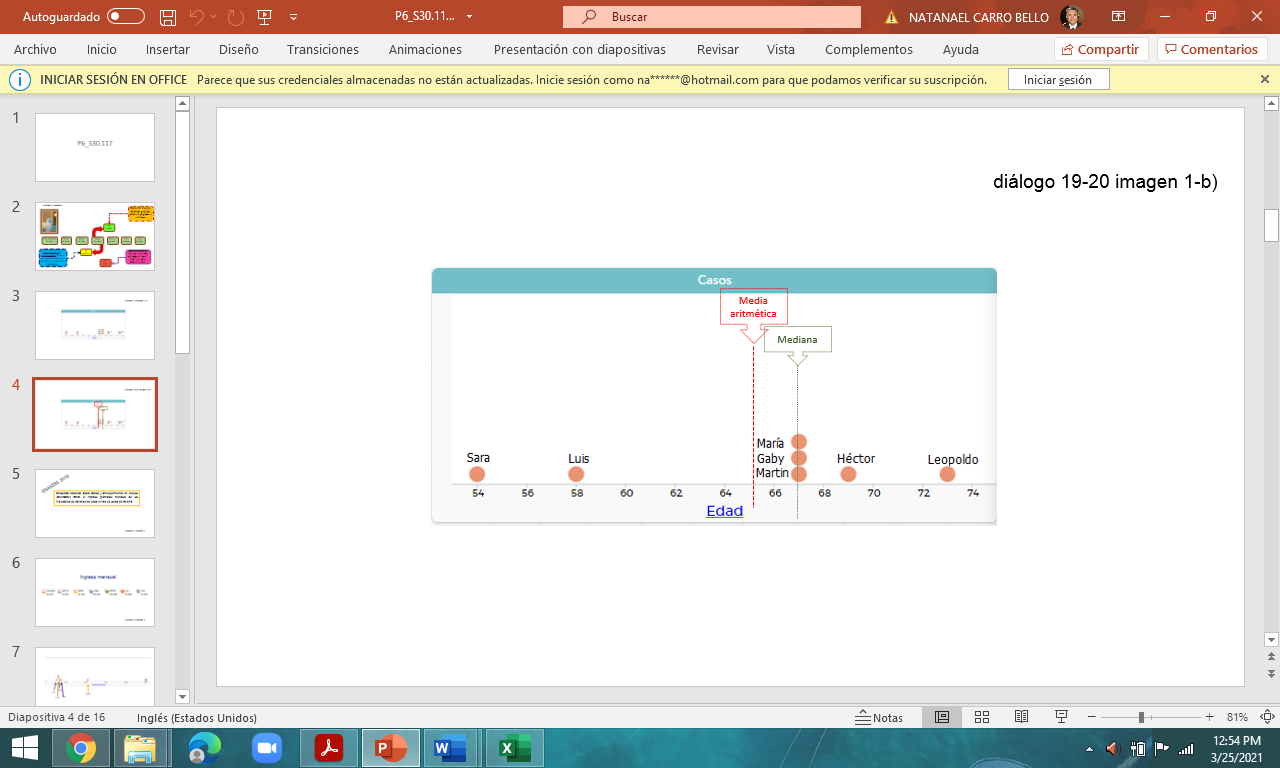
En el siguiente caso, observa que sí conviene usar el valor de la media aritmética o de la moda o de la mediana como referente.
Actividad 2
Revisa la siguiente información.
De acuerdo con la Encuesta Nacional sobre Salud y Envejecimiento en México (ENASEM) 2018, el ingreso promedio de los mexicanos de 50 años de edad o más es cerca de 3 578 pesos mensuales.
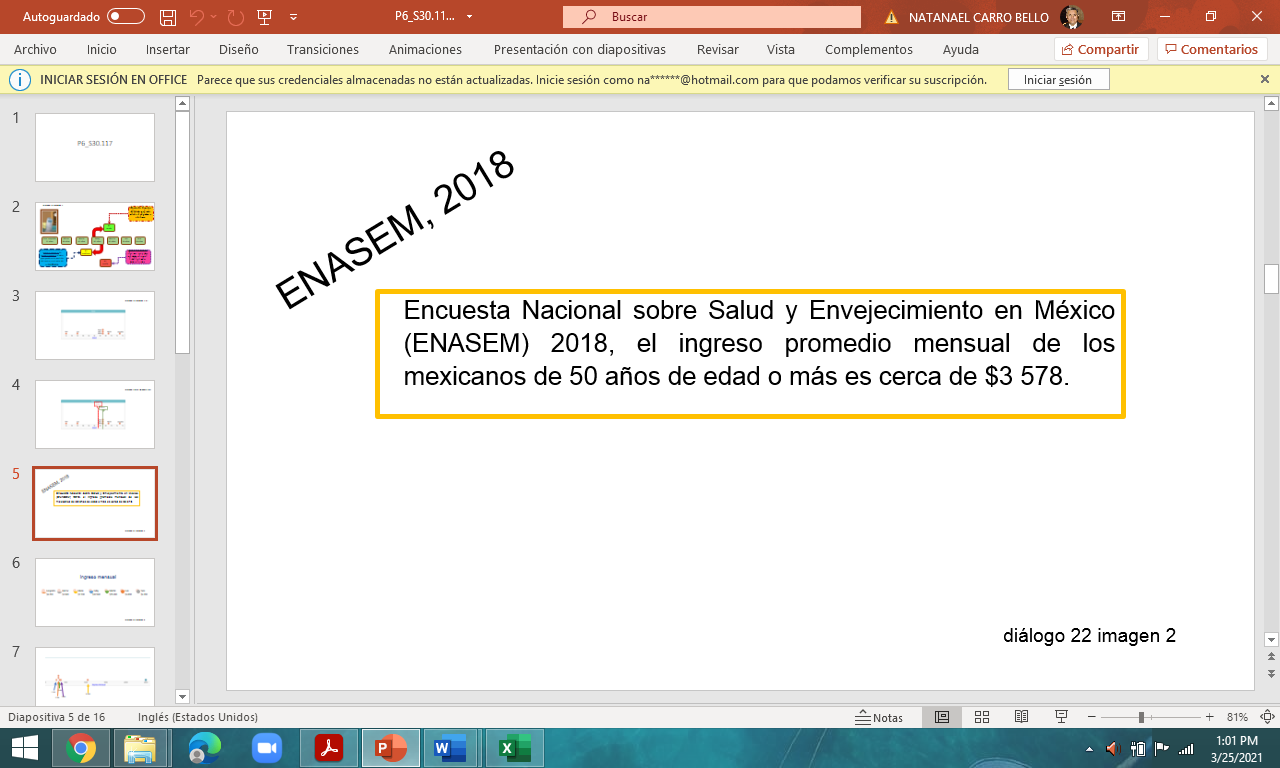
Como identificaste en el ejemplo anterior, Don Leopoldo es muy platicador y le contó a Cupertino que el ingreso promedio de sus hermanos y el de él es el doble del reportado en esta encuesta.
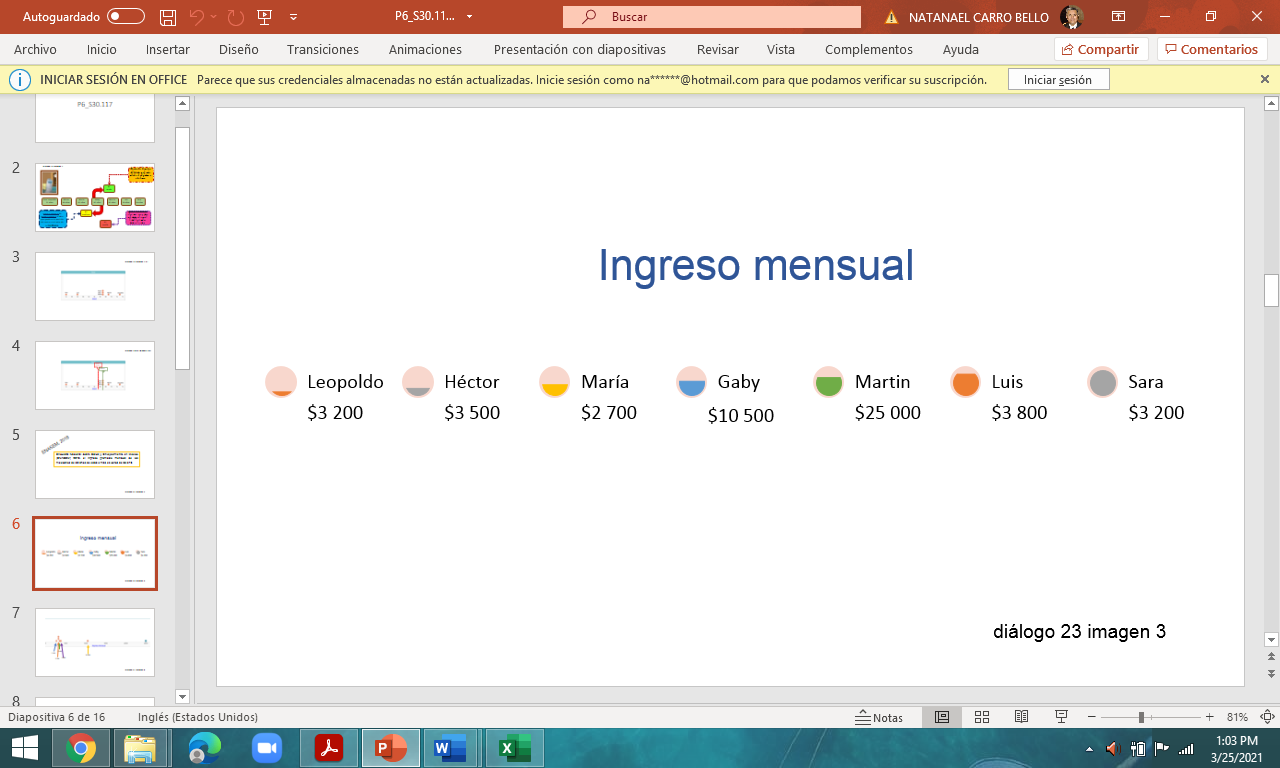
Observa los montos del ingreso mensual de los siete hermanos: Leopoldo $3,200, Héctor $3500, María $2700, Gaby $10,500, Martín $25 mil, Luis $3800 y Sara $ 3200. Ahora, responde, ¿Qué ingreso promedio se refería don Leopoldo?
Al parecer el ingreso promedio es de $3 200
¿Por qué ese dato es el más representativo de eso ingresos?
Probablemente porque es parte de los datos y es el más frecuente.
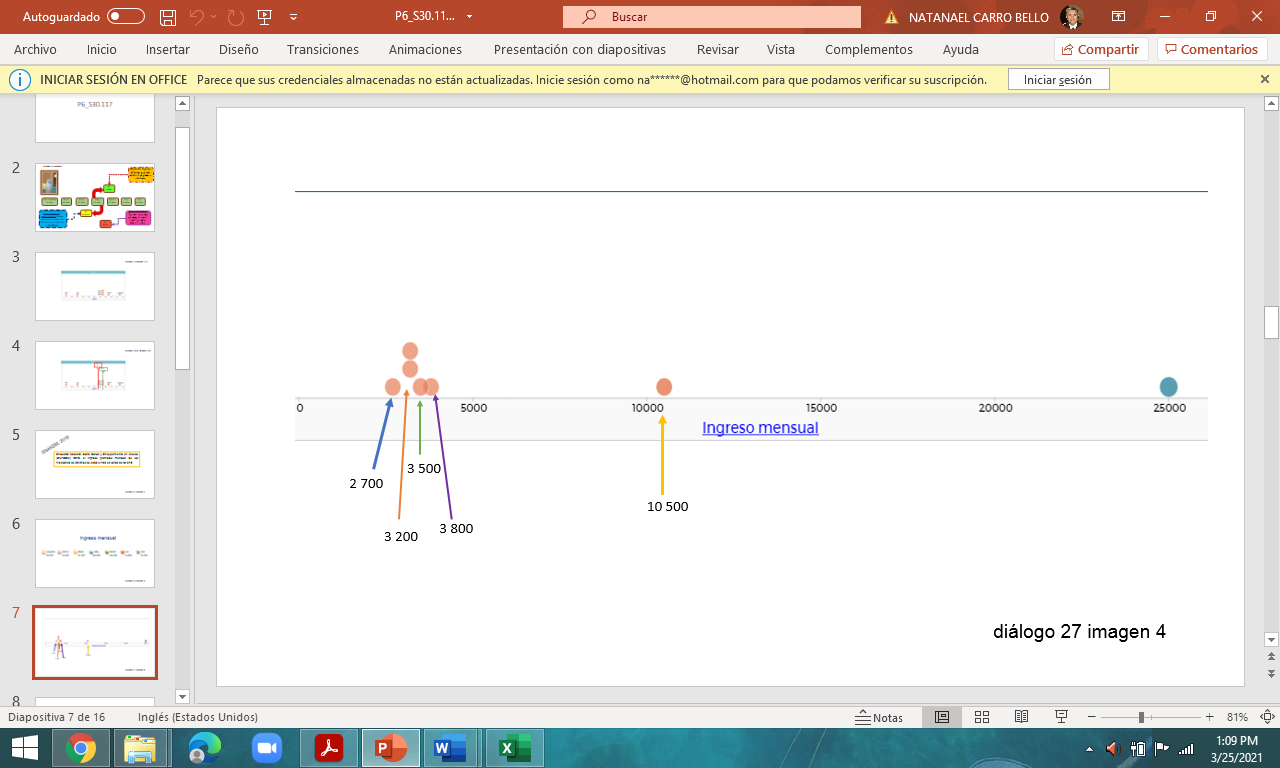
Ese es el valor de uno de los datos y es el que más aparece, como se observa en esta gráfica, pero, no olvides considerar que Don Leopoldo le dice a Cupertino que el ingreso mensual entre sus hermanos y él es el doble del referido en la encuesta.
El valor de la mediana tampoco es porque en este conjunto de ingresos, el que queda en el centro después de ordenarlos es $3500
Y ese valor es casi igual al de la encuesta.
Entonces, no queda más que analizar el valor de la media aritmética.
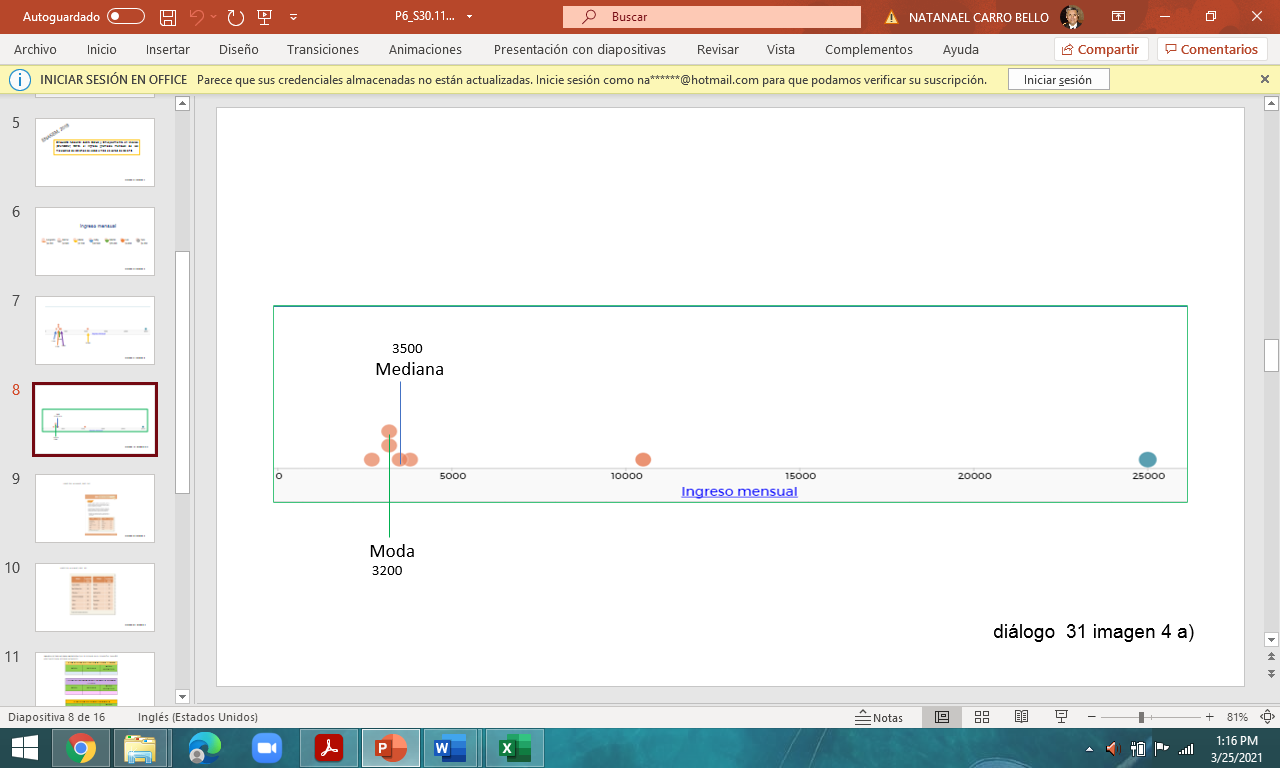
Hay que calcularlo porque se tienen que considerar todos los datos, antes. Observa los datos en la gráfica y trata de anticipar dónde quedaría ubicado el valor.
Comprueba tu predicción al calcular el valor de la media aritmética.
Suma los datos que corresponden al ingreso mensual y los divides entre 7 son siete datos porque son siete hermanos.
El resultado es: $7400
Ese era el valor al que don Leopoldo se refería, sin embargo, debes analizar si ese valor es el más representativo de este conjunto de datos. ¿Crees que ese valor es el que mejor representa los ingresos de todos los hermanos de don Leopoldo incluido él?
Conforme vayas avanzado en la clase, reflexiona más sobre cuál valor puedes elegir entre la media, la mediana y la moda como el más representativo de un conjunto de datos.
Actividad 3
Ahora trabaja con lo que te presenta el libro de texto, página 107 desafío 54 “México en números”
https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/107

¿Qué dice la consigna?
En equipos, analicen y decidan, en cada problema, cuál es la medida de tendencia central más conveniente para dar una información representativa de cada conjunto de datos, expliquen por qué lo consideraron así y calcúlenla.
La información que Inegi recaba a partir de los Censos Nacionales de Población y Vivienda y los Conteos de Población es analizada y organizada por temas para obtener estadísticas sociodemográficas de México, algunos datos interesantes son:
Distribución de la población en México. La tabla muestra, de la población total de cada entidad, el porcentaje que vive en zonas urbanas.
La consigna pide que digas: ¿Cuál es la medida de tendencia central que más conviene para representar un conjunto de datos, la media, la mediana o la moda?
Observa la tabla, ¿Qué información te proporciona la tabla?
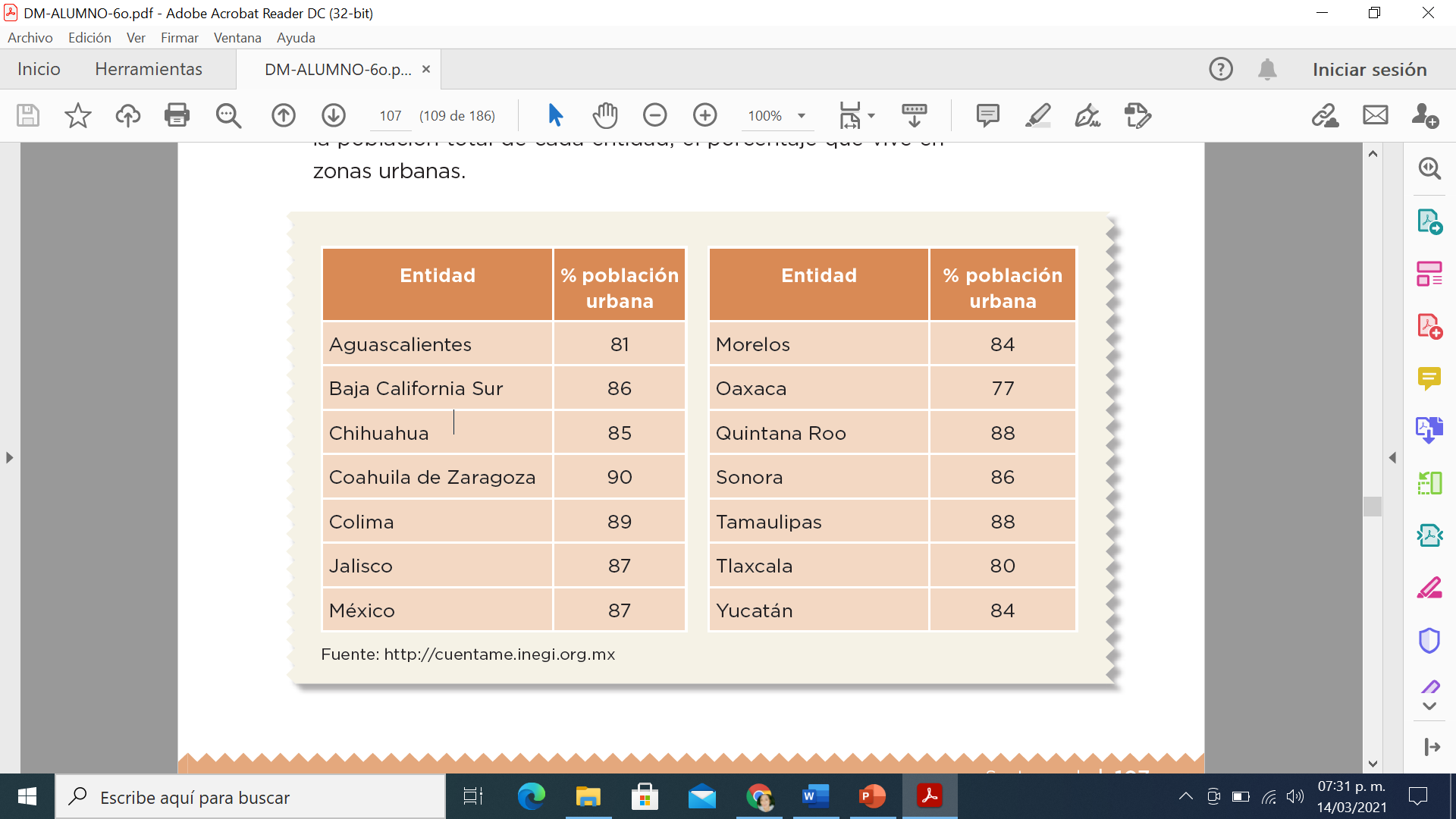
Revisa detenidamente. ¿Qué observas?
La tabla muestra el promedio de población urbana de 14 estados de nuestro país.
Presenta la media aritmética de la población que vive en zonas urbanas, es decir, muestra el porcentaje de la población que vive en ciudades que cuentan con servicios públicos y donde existen importantes actividades económicas, entre otras características.
Analiza los datos para dar respuesta a la pregunta, ¿Cuál de las medidas de tendencia central es la más representativa, la moda, la mediana o la media aritmética?
Podría ser la moda, porque son los datos que se repiten, pero hay varios que se repiten 2 veces.
No olvides registrar la información que vas encontrando.

Son el 84, el 86, el 87 y el 88
Como ves, se tiene más de un valor para representar a la moda porque hay varios datos que coinciden en la frecuencia que se presentan y además es la mayor frecuencia.
Observa en tu libro los datos y encuentra la mediana.
El que queda en medio es el 86
Registra 86 en la columna de la mediana, ¿Con estos datos crees que puedes tomar una decisión sobre la respuesta a la consigna? Puedes usar la calculadora.
La suma dio 1192 y ahora entre 14 porque son 14 datos, resulta que 85.14 es el promedio de este conjunto de datos.
Regístralo, con esto se completa la búsqueda de las medidas de tendencia central que se están comparando.
En la moda hay varios datos que se repiten 2 veces y son 84, 86, 87 y el 88, la mediana es 86 y la media aritmética es 85.14 ahora ya puedes visualizar la respuesta con su respectivo, ¿Por qué? o argumento.
El argumento es que el dato más representativo del conjunto de datos que presenta la tabla es la mediana.
¿Por qué la mediana que, en este caso es 86, es el más representativo?
Porque hay más de un valor para representar a la moda, y, en el caso de la media aritmética, es un valor que no está en el conjunto de valores de los datos y se ve afectada por el valor de datos extremos como ocurre aquí, por eso el 86 es el valor que representa mejor al conjunto de datos.
Además, porque es un dato que se encuentra dentro del mismo conjunto y aparte es uno de los que se repiten dos veces.
Es importante tener claro que se está trabajando con medidas de tendencia central, por lo tanto, el dato que es el representativo debe ser un dato en el centro de los dos extremos, o sea entre el mayor y el menor dato. Tiene que ser un punto de equilibrio.
Hay que buscar un dato cercano al centro de todos los datos, considerando los extremos, se necesita analizar los extremos: dato mayor 90 y dato menor 77 imagina que tienes una recta con los números del 90 al 77, ¿Qué número queda al centro?
Es el 83.5
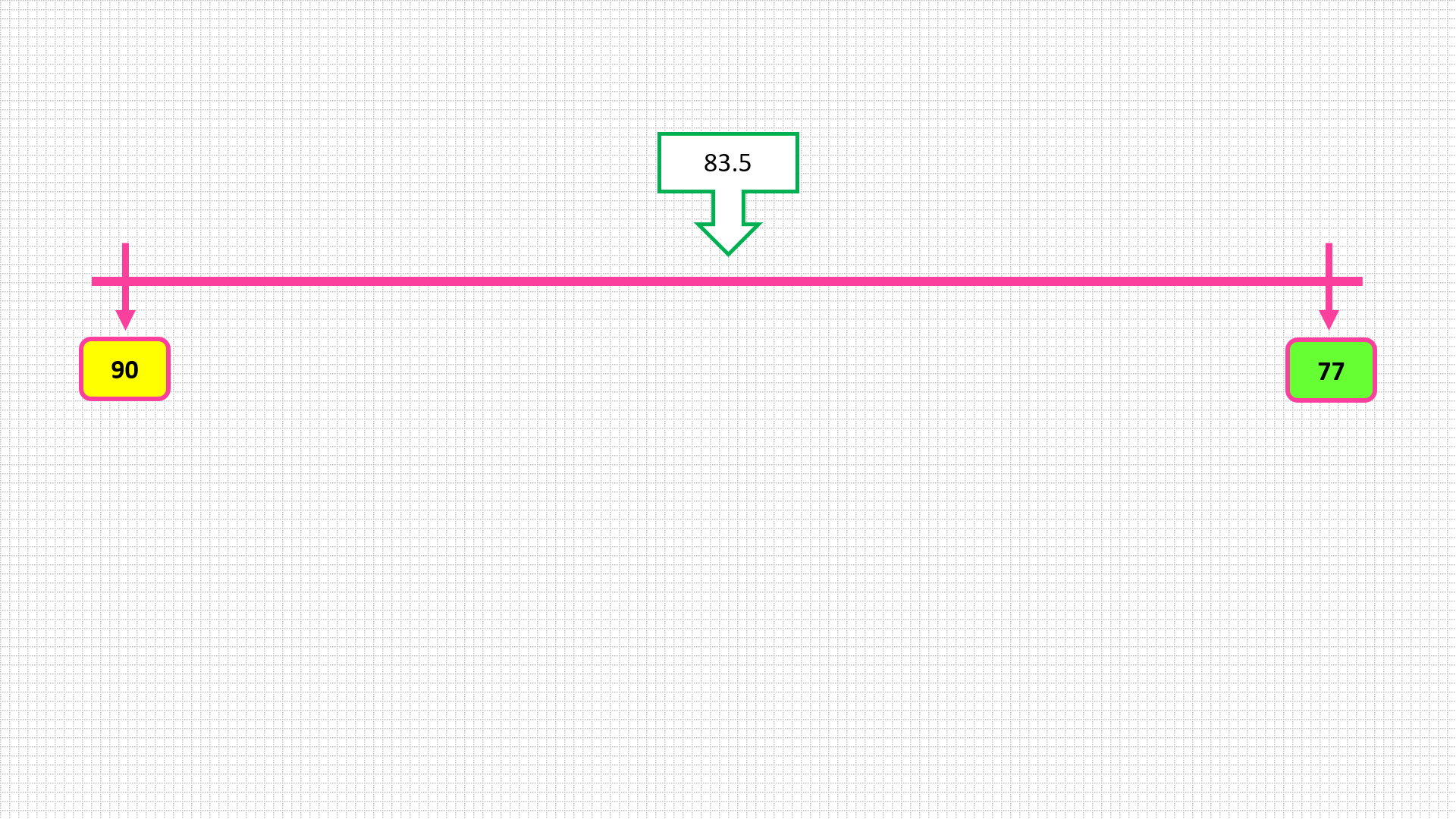
¿Qué número de los datos es más cercano al centro: La mediana o la media aritmética.
Es la media aritmética porque vale 85.14 y es el valor que está más al centro, es el más equilibrado.
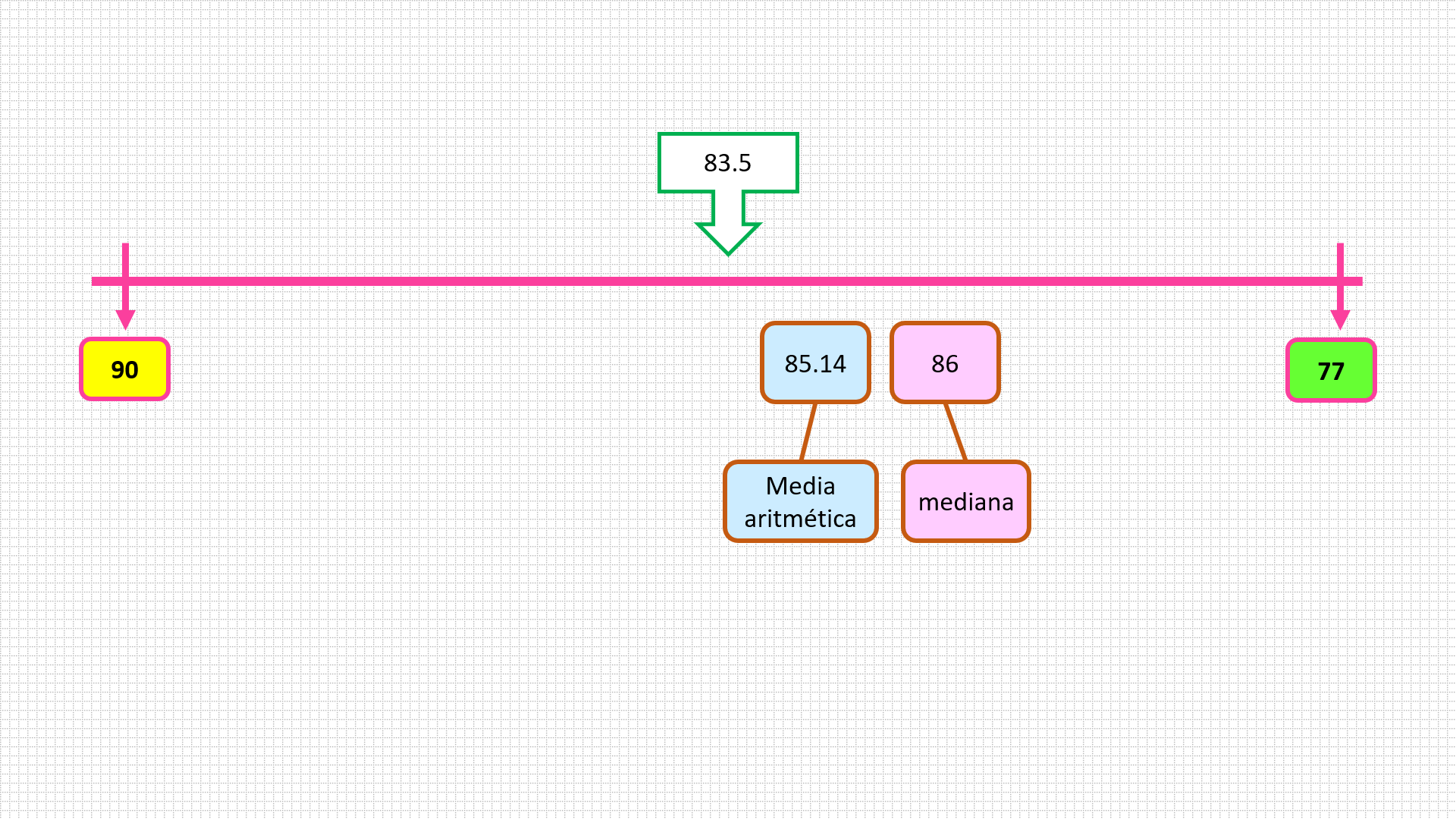
La media aritmética está más cercana al centro y se puede considerar como el punto de equilibrio de todos los datos.
Es importante que trates de comprobar tus respuestas, como pudiste observar en el ejercicio anterior, faltó considerar que la medida representativa de un conjunto de datos debe buscar el centro, por eso se llaman medidas de tendencia central.
Revisa la actividad 2 de la página 108
https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/108

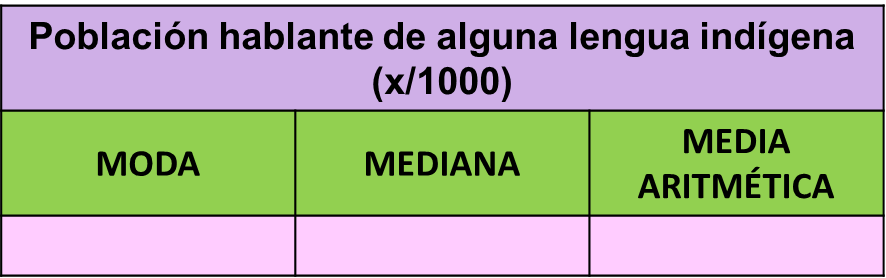
Refiere a la población que habla alguna lengua indígena. En la tabla se presenta el número de hablantes de una lengua indígena por cada mil habitantes en diferentes entidades.
Observa los datos que se presentan en la tabla. Recuerda que se está buscando la medida de tendencia central que sea la más representativa de este conjunto de datos. ¿Qué observas en los datos de la tabla?
Que hay dos datos que son más grandes y dos datos que son muy pequeños.
Esto es una muestra de que hay más personas que hablan una lengua indígena en algunos estados que en otros.
Así es, la distribución de las personas en el país varía mucho, en unos estados viven muchos hablantes de lenguas indígenas y otros estados tienen muy pocos. Lo cual es muy claro en esta tabla.
Dentro de este conjunto de datos, ¿Cuál es la moda?
Es el 10 porque es el dato que más se repite.
La mediana es 30 porque es el dato al centro, después de ordenarlos de mayor a menor.
Como pudiste darte cuenta, para el cálculo de la mediana quedaron dos datos al centro, en este caso, los dos son del mismo valor.
La media aritmética que implicó sumar los datos y dividir entre 14 es 81.92
Entonces se tiene, moda 10, mediana 30 y media 81.92
Observa mejor los datos y fíjate cuál es el más representativo de todos éstos.
Hay que tomar en cuenta que es muy importante que observes la tabla que está en tu libro, el dato mayor y el dato menor están muy separados. Analiza los datos que se encuentran registrados.
Son 10, 30 y 81.92
En este caso puedes considerar que la más representativa es la moda, el 10, observa y encuentra por qué.
Casi en todos hay 10 o más.
Ya tienes parte de la idea, sigue construyendo tu argumento.
En la mayoría de los estados registrados en la tabla, mínimo tiene 10 aunque hay otros que tienen menos.
Observando la tabla te das cuenta que la mayoría de los estados tiene mínimo 10 hablantes de alguna lengua indígena por cada 1000 personas. Únicamente dos estados quedan fuera de esta afirmación, que son Zacatecas con 4 hablantes por cada 1000 personas y Guanajuato con 3 hablantes por cada 1000 personas.
Para encontrar un dato representativo debes observar muchas cosas.
Cada tabla dependiendo la información que te brinda tendrá una forma de interpretación diferente, por ello debes ser muy observador u observadora.
Revisa la actividad 3 de la página 109
https://libros.conaliteg.gob.mx/20/P6DMA.htm#page/109
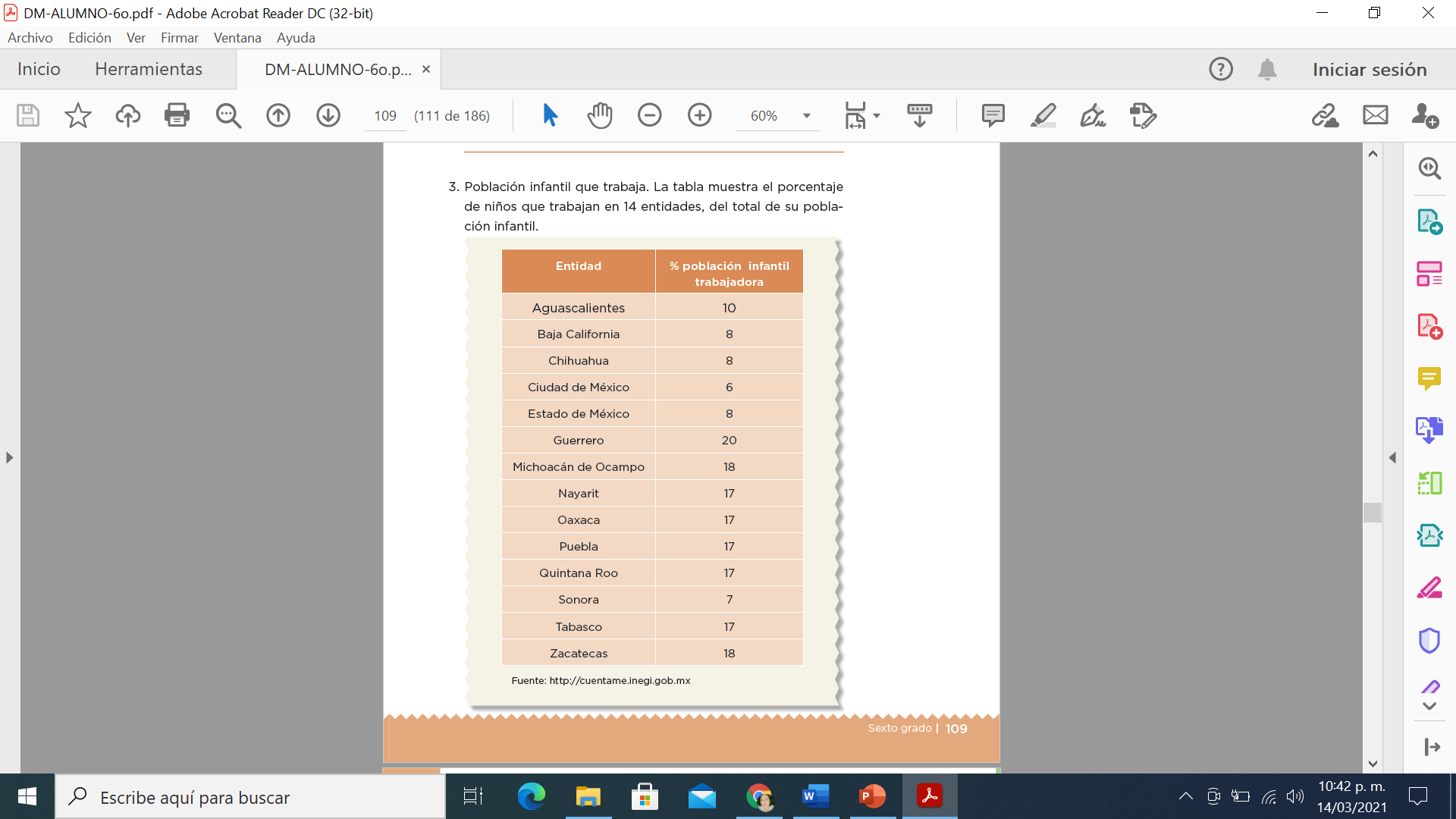
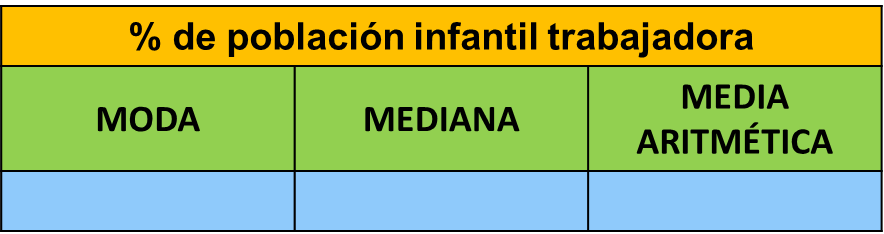
Población infantil que trabaja. La tabla muestra el porcentaje de niños que trabajan en 14 entidades, del total de su población infantil.
Observa los datos que presenta la tabla. El reto es el mismo que en los anteriores, encontrar la medida representativa. La tabla presenta el porcentaje de niños que trabajan de cada estado con respecto a su población total.
El dato que más se repite es el 17, o sea, la moda.
Ve ordenando los datos de mayor a menor para encontrar la mediana.
La mediana es 17
Ahora, calcula la media aritmética, recuerda debes sumar y dividir: 10, más dos veces 8 más 6 más 28 en total es 188 entre 13 datos, te da 13.4
La mediana y la moda, coincidieron, tienen el mismo número 17
La media es 13.4
Ya están los datos completos así que, ¿Cuál será de este conjunto de datos el más representativo?
Analiza los 3 datos obtenidos y di cuál consideras que es el más representativo de este conjunto de datos.
Realiza un repaso de lo que hoy estudiaste: Se calcularon las medidas de tendencia central, para poder encontrar y argumentar cuál de ellas era la que mejor representa un conjunto de datos, lo cual depende precisamente de los datos que se analizaron. Es muy importante que, al realizar una interpretación de cualquier tipo de información, la conozcas bien, si no, podrían hacerse afirmaciones falsas o fuera de la realidad.
También aprendiste que hay que ser más observadores de la información que se presenta en cualquier medio de comunicación.
Así es, si no alguien puede dar una información falsa y pensar que es verdad, por eso se deben analizar los datos para que te des cuenta de que es una correcta o falsa interpretación.
El reto de hoy:
Comparte lo que aprendiste con alguien cercano, explícale la importancia de saber interpretar datos y para que sirve saber el uso de la media aritmética, la mediana y la moda, apóyate en los ejemplos.
Si te es posible, consulta otros libros o materiales para saber más sobre el tema.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas