Volúmenes
Volúmenes
Aprendizaje esperado: explora las características y propiedades de las figuras y los cuerpos geométricos.
Énfasis: calcular volúmenes.
¿Qué vamos a aprender?
Los materiales que necesitarás es tu cuaderno de apuntes, lápiz o bolígrafo, y una calculadora para agilizar las operaciones.
En el concepto de volumen, existen distintas situaciones para explicarlo.
¿Qué hacemos?
Revisa la primera situación:
Cuando se elige un recipiente ¿Cuál es su capacidad? Es decir, los recipientes para almacenar alimentos tienen una medida que generalmente aparece en mililitros cuando son pequeños, por ejemplo, los envases de bebidas o de dulces.
En el caso de recipientes más grandes, la medida es en litros o galones, como los envases de bebidas o de algún tipo o pinturas.
Esto se puede reconocer en los envases de leche cuya capacidad es de 1 litro.
Esa marca de 1 litro es la capacidad para almacenar del envase. Por lo tanto, es la cantidad de leche contenida.
Basándose en lo anterior, ¿se puede acertar la diferencia entre volumen y capacidad?
El volumen es la cantidad de espacio que ocupa un cuerpo, mientras que la capacidad es la cantidad de espacio que contiene.
En el caso de los recipientes, es la cantidad que tienen para albergar algo.
Entonces, todos los objetos con tres dimensiones tienen un volumen, es decir, ocupan una cantidad de espacio.
Por ejemplo: Una goma, una regla o sus libros de texto, pero éstos no tienen una capacidad para albergar un contenido. Sin embargo, el recipiente en donde se contiene agua o el desayuno para el receso tiene volumen y capacidad.
¿Qué otros objetos tienen volumen y capacidad?
Por ejemplo, cuando te enfermas y el doctor te receta un jarabe o una solución; el envase tiene un volumen el cual se puede calcular en centímetros cúbicos y su contenido viene marcado en mililitros.
Los envases de medicina son recipientes con la capacidad de albergar contenido en su interior, y el volumen de éstos es el espacio que ocupa la botella.
En México se emplea el Sistema Internacional de Unidades. En el caso del volumen se utilizan los metros cúbicos y sus múltiplos y submúltiplos, como el centímetro cúbico y el decímetro cúbico, unidad que resulta ser equivalente a la unidad litro de capacidad, aunque esta última no pertenezca al Sistema Internacional.
En algunas ocasiones las medidas son mayores o menores a un litro, por lo que también se utilizan múltiplos y submúltiplos del litro. Para estos casos, se puede expresar una medida como se plantea en el siguiente caso.
Se tiene una imagen en la que se representa un recipiente con capacidad de un litro. Sin embargo, si se requiere una porción más pequeña, se divide en 100 partes.

Se le conoce por el nombre de centilitro.
Y en el caso de requerir una parte o porción más pequeña se puede dividir en mil partes. Por lo tanto, se tiene un mililitro.
Se puede entender cómo los mililitros son una milésima parte de un litro, y esa es la medida más usada en las porciones requeridas, por ejemplo, para una receta de cocina o en los vasos de agua consumidos a diario.
Así también, para la capacidad de los cuerpos con volumen, se emplea la misma unidad de medida, los mililitros.
Aunque, si la capacidad de los cuerpos con volumen o sólidos se pueden medir en litros -o con partes más pequeñas como centilitros o mililitros- ¿Por qué se resuelven problemas de cuerpos con volumen cuyas medidas están expresadas en centímetros o metros cúbicos?
Cabe resaltar que, existe una relación entre los metros cúbicos que un cuerpo tiene de volumen y su capacidad de almacenamiento que se mide en litros.
Se tiene un cubo de 10 cm por lado.
Pero ¿Cuántos centímetros hay en un decímetro?
Un decímetro tiene 10 centímetros, se tiene así que el cubo mide 1 decímetro por lado.
Y para calcular su volumen se multiplica el largo, el ancho y la altura. Es decir, 1 por 1 por 1, teniendo como resultado que el volumen de este cubo es 1 decímetro cúbico.
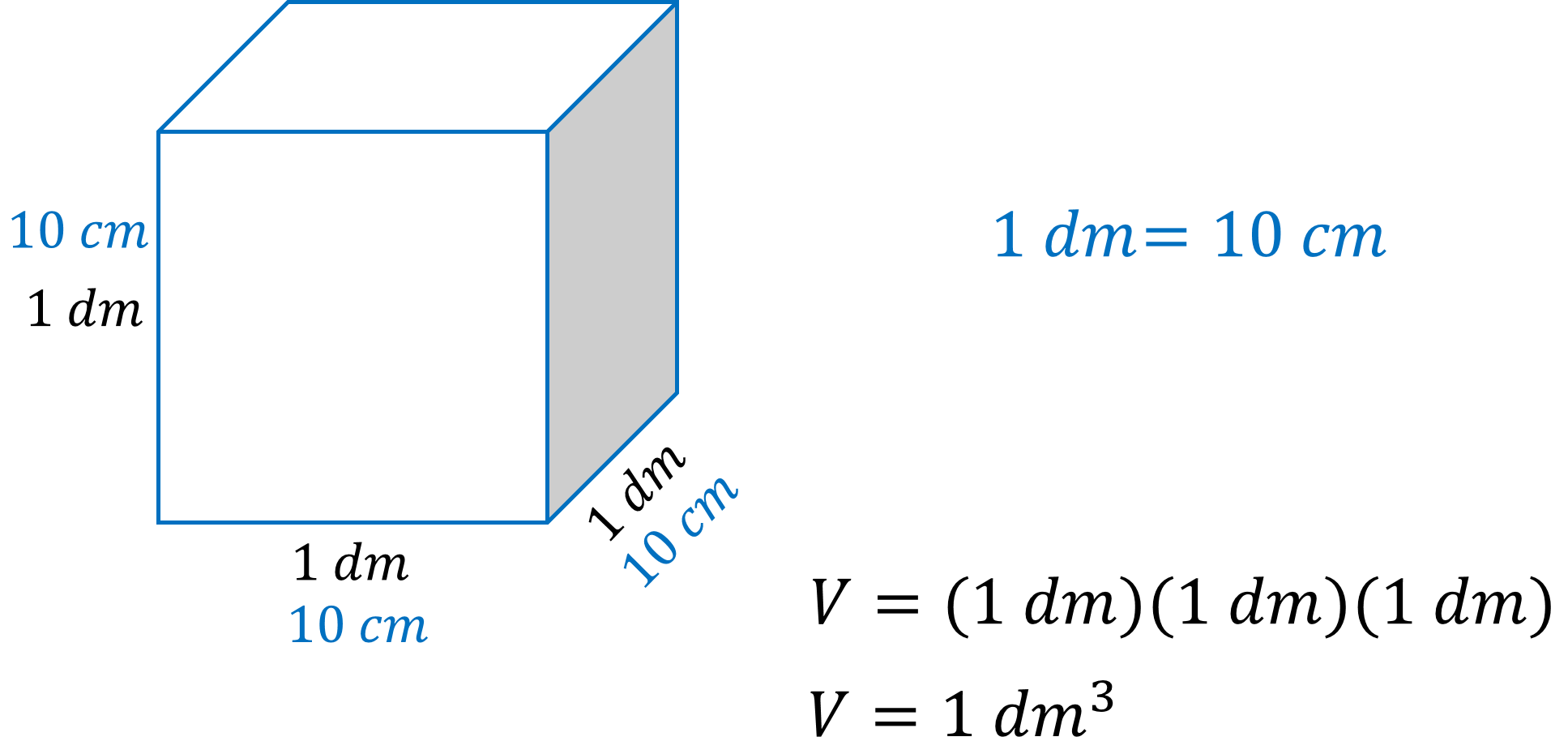
El cubo, al igual que los envases de medicina o recipientes para guardar comida, tiene una capacidad de almacenamiento.
Es así como se tiene por objetivo, conocer su equivalencia:
Se sabe que un cuerpo con un volumen de 1 decímetro cúbico tiene la capacidad de almacenar 1 litro, es decir:
1 litro es equivalente a 1 decímetro cúbico.
Por lo tanto, el cubo tiene un volumen de 1 decímetro cúbico, y la capacidad de 1 litro.
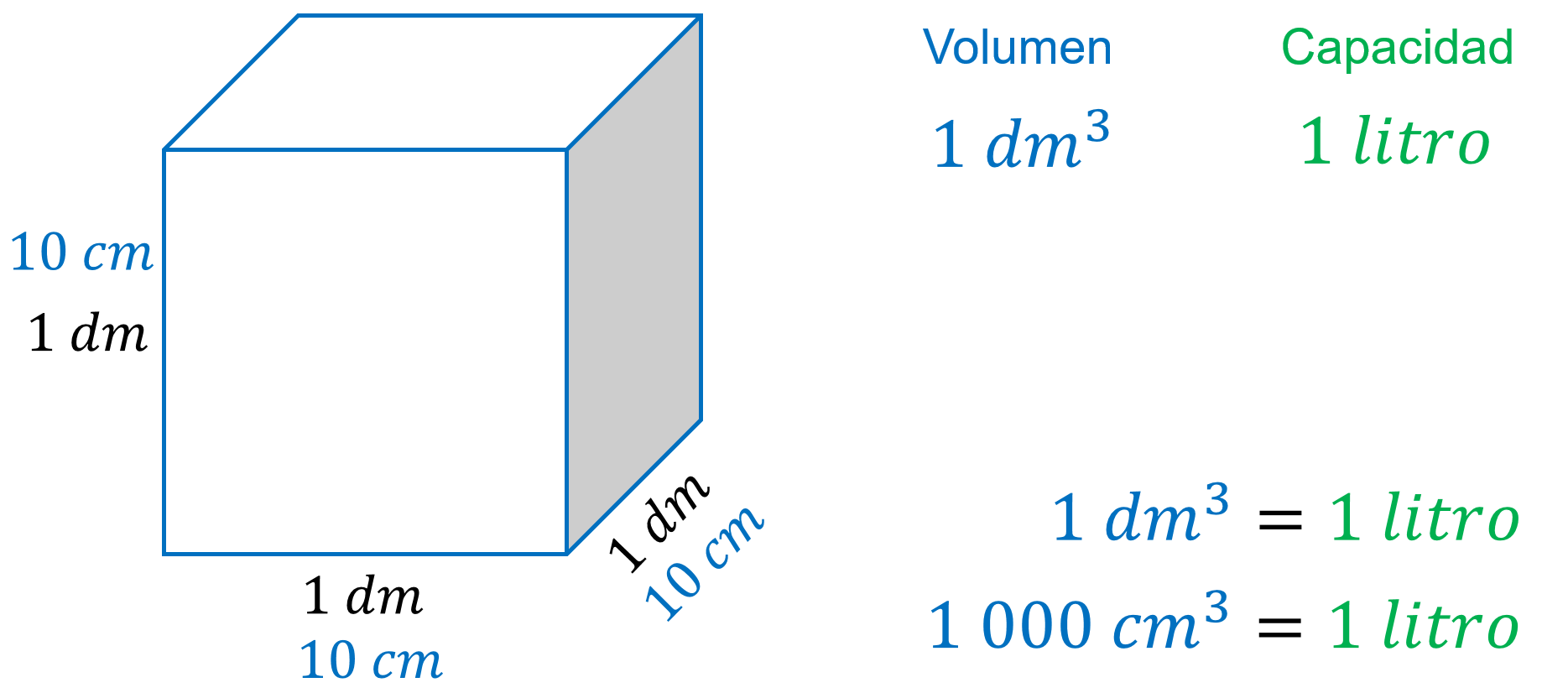
Y si 1 decímetro tiene 10 centímetros, 1 decímetro cúbico son 1 000 centímetros cúbicos
De este modo, 1 000 centímetros cúbicos equivalen a una capacidad de 1 litro.
Ya conoces las diferencias entre prismas y pirámides, y sabes que las fórmulas para calcular el volumen son diferentes.
Para el caso del cubo, las tres medidas son iguales y su volumen se obtiene al multiplicar lado por lado por lado, o bien, elevando al cubo o aplicando la tercera potencia de la medida del lado.
Asimismo, ya conoces las diferencias entre las pirámides: La pirámide pentagonal o cuadrangular que se reconocen en color azul y los prismas rectangulares, cuadrados, rectangulares o triangulares, en rojo.
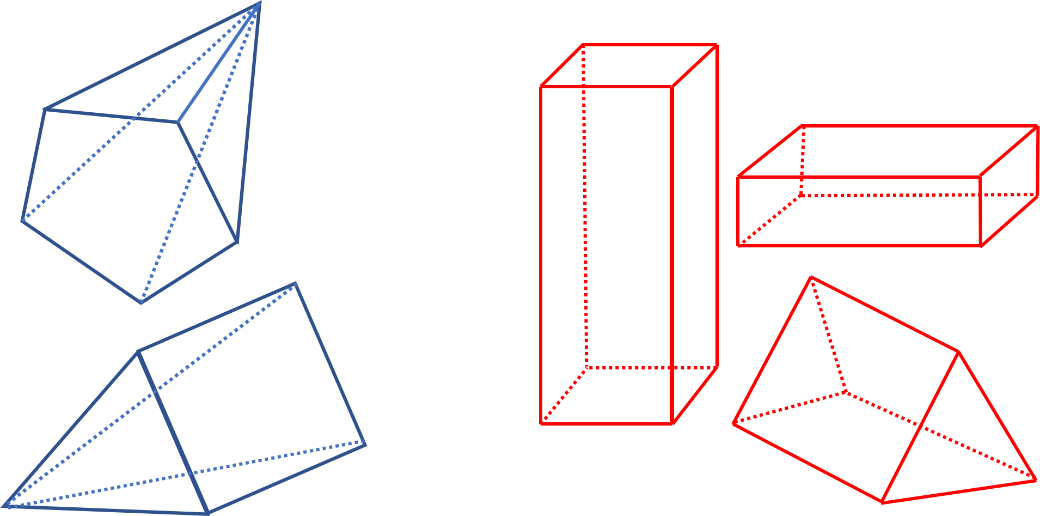
Sin embargo, se tienen otros sólidos que no se pueden considerar ni pirámides ni prismas.
¿Usted se refiere a cuerpos con volumen que no son pirámides ni prismas? ¿Cuáles son?
Son los Sólidos Platónicos.
Este nombre se le atribuye al filósofo y matemático Platón, quien fue el primero en estudiarlos.
Los Sólidos Platónicos son cinco cuerpos geométricos con un conjunto de características que comparten.
Éstos sólidos también reciben el nombre de Sólidos Perfectos o Poliedros Platónicos. Sus características en común son:
Se tiene que son sólidos regulares de caras idénticas.
Y los ángulos interiores son iguales; ya se sabe que estos ángulos reciben el nombre de diedros.
Del mismo modo, las aristas tienen la misma longitud, es decir, el segmento de recta en donde se unen 2 caras iguales.
Y en todos los vértices se tiene que concurren el mismo número de caras y la arista.
Éstas son las características generales que comparten todos estos sólidos, pero ¿Cuáles son sus características individuales?
Cada sólido tiene características particulares, y ustedes en casa identifiquen para cada sólido platónico lo que se detalla a continuación.
El primer sólido es el Tetraedro, conformado por caras en forma de triángulo equilátero.
Observa la figura amarilla, que es el desarrollo plano del tetraedro, lo cual significa que así se ve el cuerpo cuando está desarmado.
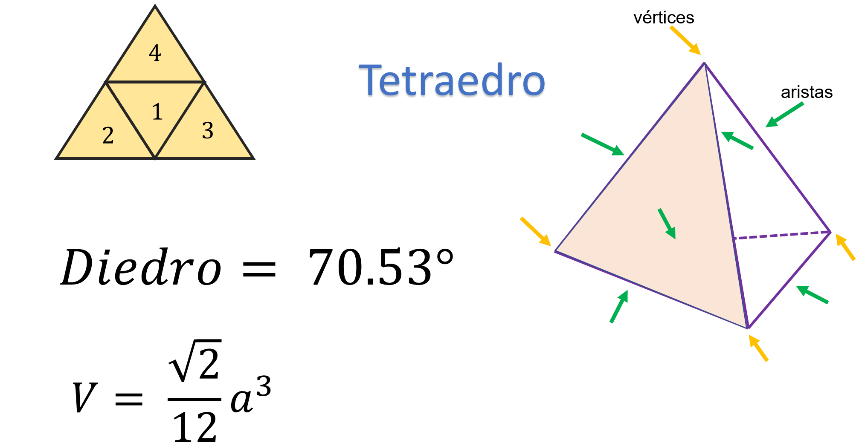
En total tiene 4 caras, de ahí su prefijo “tetra” que significa cuatro.
Tiene 4 vértices, 6 aristas, y la medida de sus ángulos interiores es de 70.53 grados.
Para calcular su volumen, la fórmula es igual a la raíz de dos dividido entre 12, que, a su vez, se multiplica por la medida de la arista elevada al cubo.
El siguiente poliedro es un hexaedro que normalmente se le denomina “cubo”, algunos de estos sólidos ya se conocían, y aquí está la evidencia.
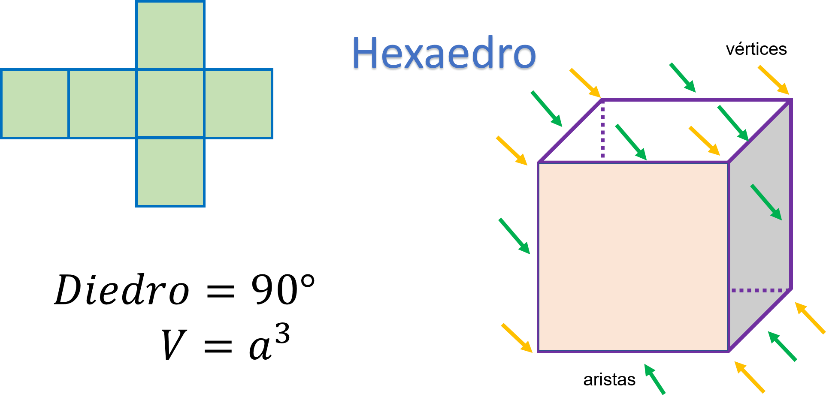
Las características principales del hexaedro son:
Tiene 6 caras cuadradas, de ahí su prefijo “Hexa” que significa 6.
Su desarrollo plano se presenta en color verde, y está conformado por 8 vértices y 12 aristas.
La medida de sus ángulos interiores es 90 grados.
Para calcular el volumen del hexaedro o cubo, la fórmula es igual a multiplicar la medida de cualquier arista del hexaedro por sí mismo 3 veces. Es decir, la longitud del lado elevado al exponente 3 o al cubo.
De este modo, se hace notorio el origen de la expresión “cúbica”.
El siguiente sólido tiene 8 caras, por lo que ya sabes su nombre: Octaedro, cuyo prefijo “octa” significa ocho.
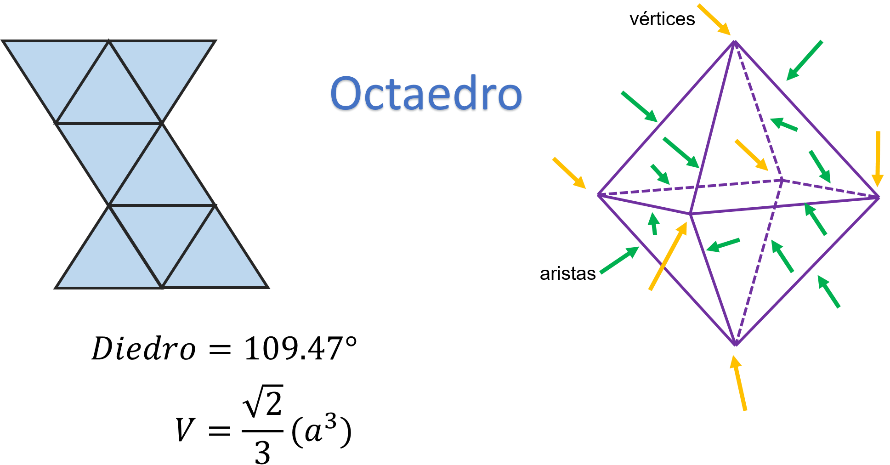
Sus caras al igual que el tetraedro, son triángulos equiláteros como se muestra en el desarrollo plano.
Tiene 6 vértices, 12 aristas, y sus ángulos internos miden 109.47 grados
En el caso del octaedro regular, la fórmula para calcular el volumen es igual a la raíz cuadrada de 2, dividida entre 3 y el resultado se multiplica por la medida de la arista elevada al exponente 3.
Por otra parte, el sólido que se tiene en la diapositiva recibe el nombre de icosaedro.
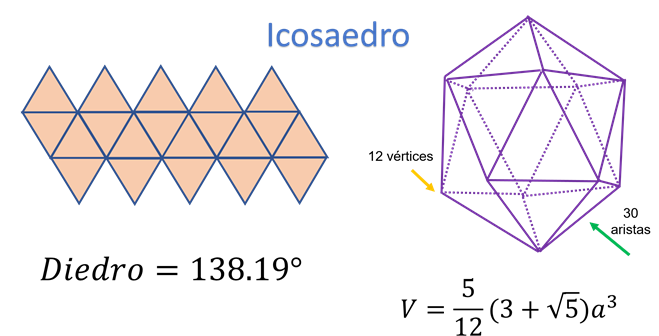
Cuenta con 20 caras de triángulos equiláteros; “icosa” es el prefijo que se refiere a “20”, y cuyo desarrollo plano al ensamblarse, cuenta con un total de 12 vértices y 30 aristas.
Sus ángulos internos miden 138.19 grados, y la fórmula para calcular su volumen es igual a multiplicar cinco doceavos por el resultado de la suma de 3, más la raíz de cinco, y este resultado a su vez se multiplica por la medida de la arista al cubo.
El siguiente sólido es el dodecaedro, formado por 12 caras de pentágonos regulares, como se muestra en su desarrollo plano; “dodeca” significa 12.
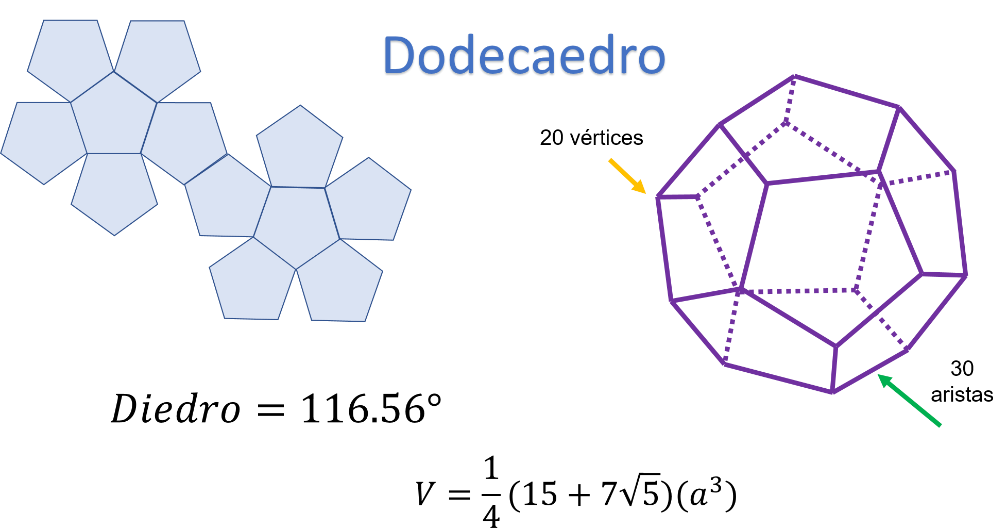
Se conforma de 20 vértices, su número de aristas es 30, y sus ángulos internos miden 116.56 grados.
En el caso del dodecaedro, la fórmula para calcular el volumen es quince más el producto de 7 multiplicado por la raíz de cinco. Este resultado se divide entre 4 y finalmente, se multiplica por la medida de la arista elevada al cubo.
Para cada fórmula expresada se puede practicar con la resolución de nuevos problemas.
Revisa un par de situaciones:
Se tienen dados en forma de hexaedro, cuya medida por lado es de 2 centímetros; además se tienen dos recipientes como los mostrados en la diapositiva.

El primero es un prisma de base octagonal irregular, cuya base está formada con 5 cuadrados de 6 cm de lado y 4 triángulos de 6 cm de base y altura, como se muestra en la figura, el prisma tiene 14 cm de altura.
Y un prisma rectangular con una base de 20 cm de largo, y 6 cm de ancho.
De los anteriores, se necesita responder: ¿En cuál de los dos contenedores caben más dados?
Ese es un problema muy específico.
No olvides anotar en tu cuaderno la información dada, y tener a tu alcance la calculadora.
Lo primero por realizar es obtener el volumen del hexaedro, que mide 2 cm por cada lado.
Su volumen se obtiene mediante la fórmula que es igual a la medida de la arista al cubo.
Es decir, 2 al cubo; al realizar la operación 2 por 2 por 2, el volumen del cubo es igual a 8 centímetros cúbicos.
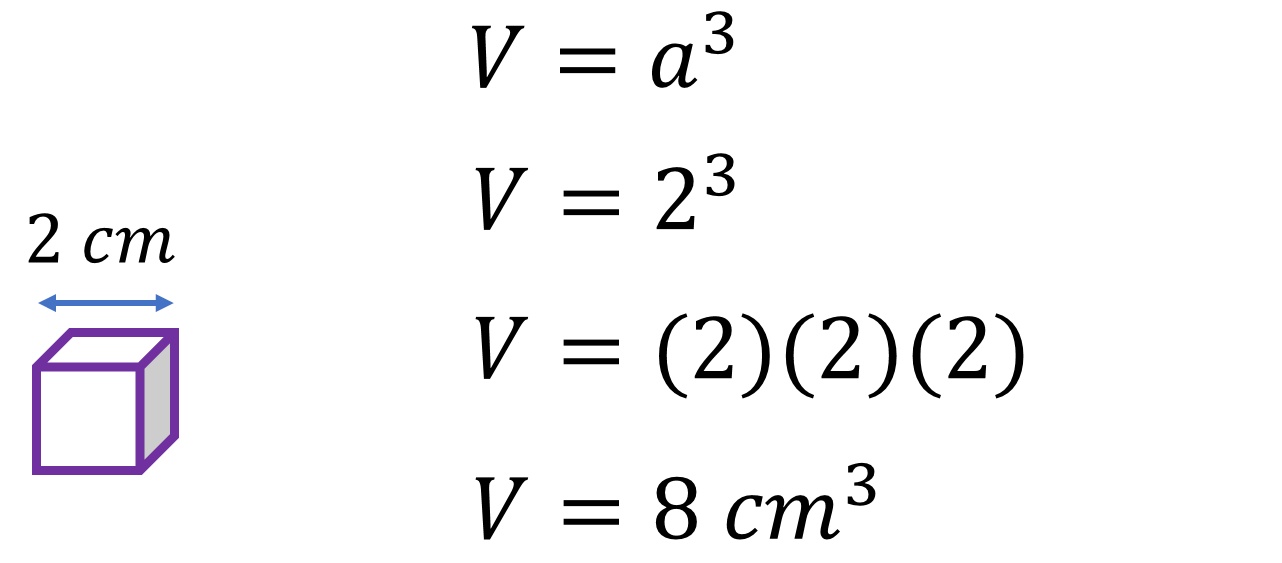
Después se obtienen los volúmenes para ambos contenedores, del que se elige indistintamente para esta ocasión, el prisma rectangular.
Observa, como se trata de un prisma rectangular, su volumen se obtiene al multiplicar el área de la base por la altura.
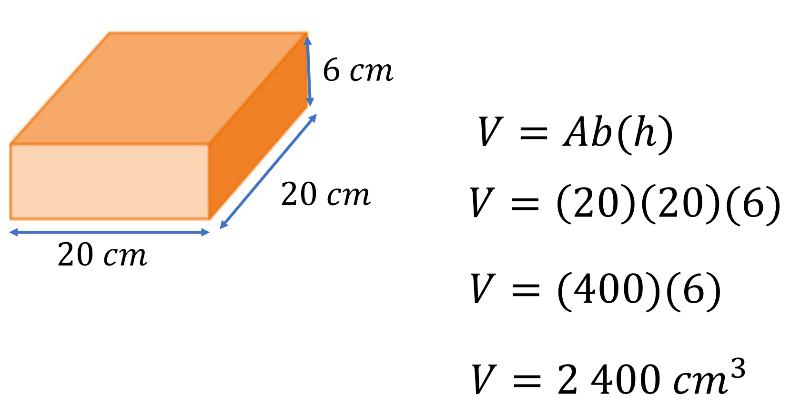
En este caso, las operaciones son 20 cm de largo por 20 cm de ancho igual a 400 cm cuadrados.
Este resultado se multiplica por la altura del prisma, que es de 6 centímetros, y se obtiene como resultado 2 400 centímetros cúbicos, que es el volumen del prisma rectangular.
Pero ¿cómo se sabe cuántos hexaedros puede contener el prisma?
Conociendo el volumen del hexaedro, es decir, de cada dado y del prisma rectangular.
El volumen del dado es de 8cm cúbicos.
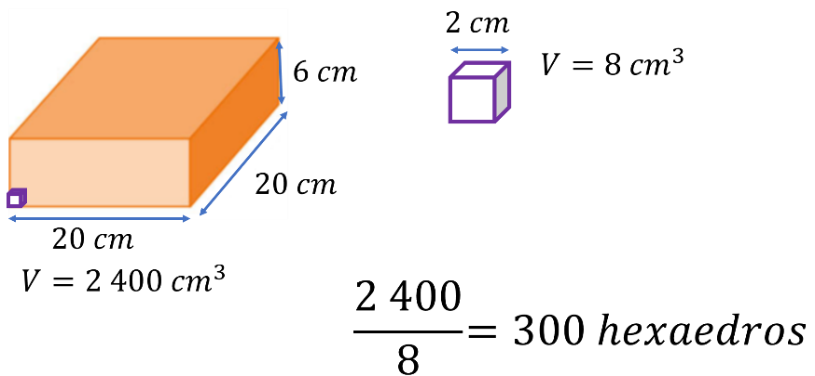
De este modo se divide el volumen del prisma entre el volumen del dado.
Es decir, 2 400 entre 8 y el resultado es 300.
Eso significa que dentro del prisma rectangular caben 300 hexaedros.
Es así como ya se puede seguir con el prisma de base octagonal irregular y conocer su volumen.
Existe un pequeño problema: En el caso del prisma rectangular, para calcular el volumen la fórmula es multiplicar el área de la base por la altura, pero no tienes el dato del área de la base del prisma octagonal irregular.
Ese dato se puede calcular a partir de las áreas que conforman a la base, pero en este caso, es posible resolverlo geométricamente tras analizar el problema.
Se conoce la medida del hexaedro de 2 centímetros de arista. Incluso se puede observar que la base del prisma octagonal está dividida en cuadrados y triángulos.
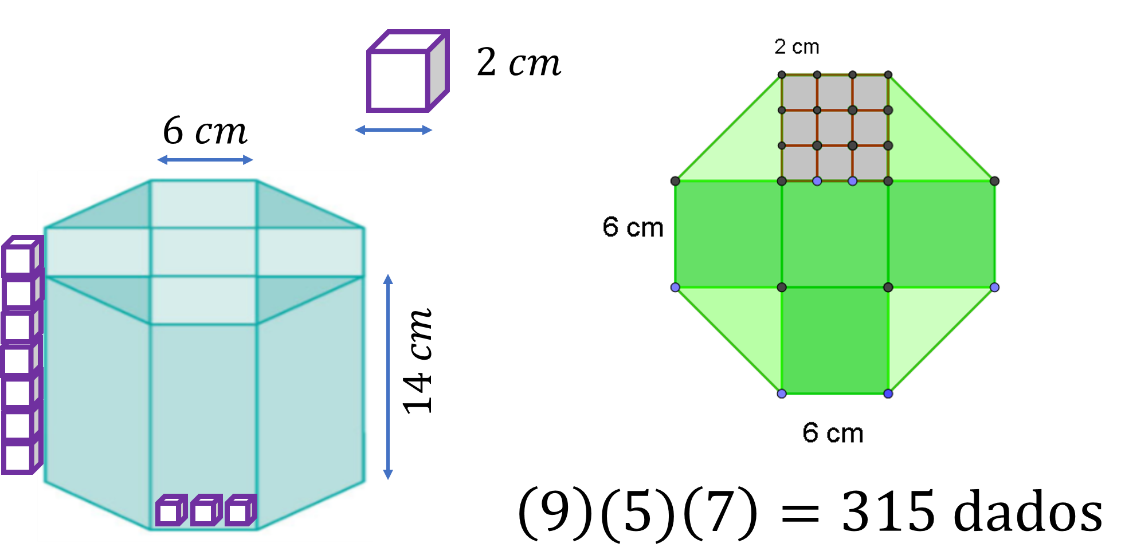
¿Cuánto miden los lados de los cuadrados en los que está dividido el octágono?
Miden 6 centímetros por lado.
De este modo, si la cara del hexaedro mide 2 centímetros por lado ¿Cuántos hexaedros caben en una de esas caras?
Caben 9 dados o cubos, por cada cuadrado dibujado en la base del prisma octagonal, porque en 6 cm caben 3 dados de 2cm, y el cuadrado es de 6 por 6.
También hay 5 cuadrados que forman una cruz en la base del prisma octagonal.
Y para el caso de la altura del prisma que mide 14 cm, como los dados miden 2cm de alto, caben 7 hileras de dados.
Por lo tanto, para saber de forma parcial cuántos dados caben en el recipiente octagonal, se multiplican los 9 dados que caben en cada cuadrado por los 5 cuadrados por 7 hileras de altura.
Teniendo como resultado 315 dados completos.
Cabe aclarar que los 315 dados no ocupan todo el volumen del prisma octagonal, porque quedan espacios correspondientes a los triángulos de la base.
Entonces, 315 dados.
Has estudiado los Sólidos Platónicos, y cuerpos geométricos como pirámides, conos y prismas rectos, así como sus propiedades para calcular volúmenes dentro de otros volúmenes.
Comenta con tus compañeros y maestra o maestro de Matemáticas si conoces otras características de estos sólidos y su aplicación en diversos problemas.
Ahora ya sabes que existen nuevas formas para practicar tus conocimientos.
Realiza el siguiente ejercicio:
Si se pudieran partir los dados o cubos por la mitad, a través de la diagonal ¿Cuántos dados más, además de los 315, caben en el recipiente en forma de prisma octagonal?
Pero, ¿qué figura se forma si cada dado se corta justo por su diagonal?
Al trazar la diagonal en ambas bases del cubo, cortarlo y separar las dos partes, se forman dos prismas triangulares
¿Y cuáles son sus medidas?
La base triangular de este nuevo prisma mide 2cm de base y 2 cm de altura del triángulo, mientras que la altura del prisma es de 2cm.
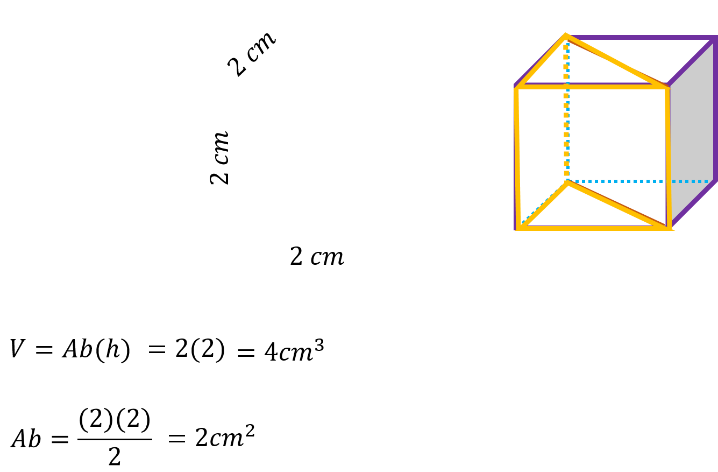
¿Cuál es el volumen del nuevo prisma o dado triangular?
Como es un prisma triangular, su volumen es igual al área de la base por la altura.
El área de la base es igual a 2 por 2, entre 2, es decir, la base del prisma triangulara tiene un área de 2cm cuadrados
Y el volumen es igual a 2 cm cuadrados por 2 cm de altura, es decir, su volumen es de 4 cm cúbicos.
¿Cuántos dados más de forma triangular o dados a la mitad caben en el reciente en forma de prisma octagonal irregular, además de los 315 cubos completos que ya están dentro?
Se observa que en el dado original su volumen es de 8cm cúbicos y en el dado cortado, su volumen es de 4cm cúbicos, es decir, una vez cortado su volumen es la mitad.
Entonces ¿Cuántos dados triangulares más caben?
Ahora en la base, caben 9 dados triangulares o medios dados, por 4 tantos, y por 7 hileras de 2cm, que resultan en252 medios cubos, lo que equivale a 126 cubos de 8 cm cúbicos.
Por lo que en total se tienen 315 cubos completos más 126 cubos armados por dos dados triangulares, resultando que en total se tienen 315+126= 441 cubos de 8cm cúbicos cada uno, así el volumen del prisma es 441 x 8= 3528 cm cúbicos.
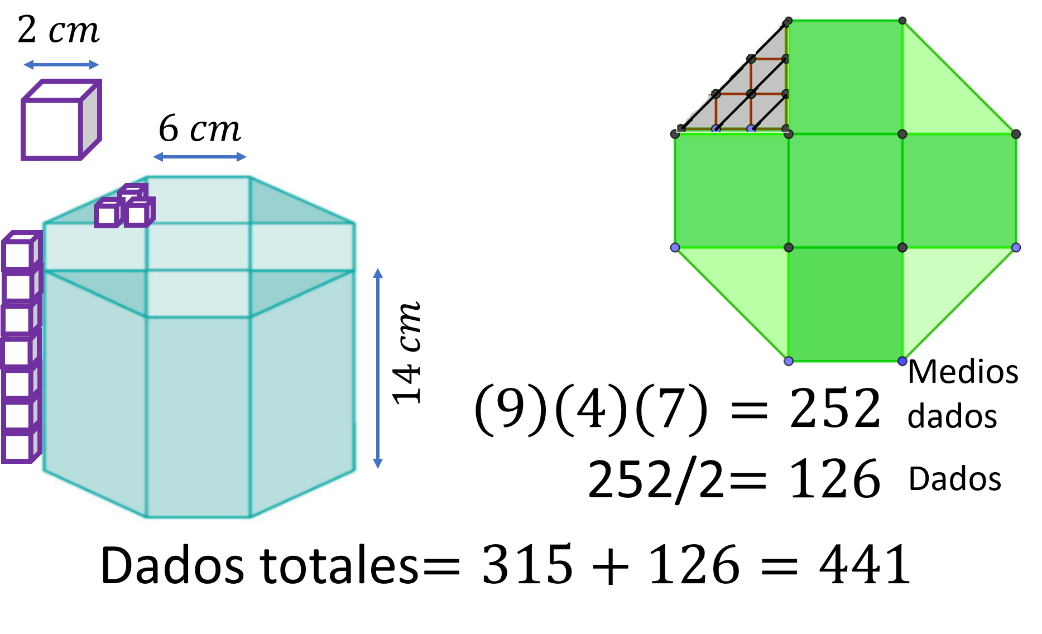
Al inicio de este problema se mencionó que no se tenía el área de la base del octágono irregular, calcula el área y comprueba el resultado anterior.
¿Puedes calcular el área sumando las áreas que conforman la base del octágono?
Se tienen 5 cuadrados de 6 por 6 cm, lo que resulta en 5 cuadrados de 36 cm cuadrados, entonces su área es de 5 x 36 = 180 cm cuadrados más el área de 4 triángulos de área igual a 4 por base 6 por altura 6 entre 2 igual a 4 por 36 entre 2 igual a 4 por 18 igual a 72, sumando las áreas de los cuadrados y los triángulos se tiene que 180 + 72 es igual a 252 cm cuadrados.
El área de la base es 52 cm2.
Entonces el volumen es área de la base por altura igual a 252 cm2 por 14cm igual a 3, 528 cm3, que divididos entre 8 cm3 por cubo, tienes 441 dados o cubos.
Comprueba tus resultados.
Responde la pregunta ¿Qué figura contiene más cubos o dados?
El prisma recto de base octagonal irregular.
El reto de hoy:
Reflexiona: ¿qué forma deberían tener los dados para ocupar todo el espacio del recipiente en forma de prisma octagonal?
Se te invita que junto a tus maestras, maestros y compañeros encuentres en tu libro de texto otros problemas y situaciones similares a las que se trataron en la sesión, y así profundizar en tus aprendizajes.
¡Buen trabajo!
Gracias por tu esfuerzo.