Volumen del cono
Volumen del cono
Aprendizaje esperado: resuelve problemas que implican calcular el volumen de cilindros y conos o cualquiera de las variables que intervienen en las fórmulas que se utilicen. Anticipa cómo cambia el volumen al aumentar o disminuir alguna de las dimensiones.
Énfasis: dar sentido y significado a la variación de alguna de las dimensiones del volumen en conos.
¿Qué vamos a aprender?
En esta sesión estudiarás cómo cambia el volumen al aumentar o disminuir alguna de sus dimensiones.
Se te pide que tengas a la mano tu cuaderno, lápiz, goma o bolígrafo.
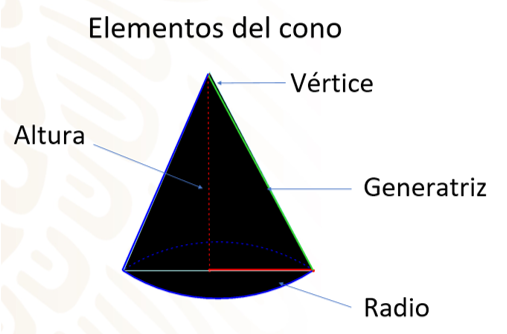
Inicia con el siguiente cuerpo geométrico: el cono. Los elementos de un cono son: base, altura, radio, vértice y generatriz.
En geometría, un cono recto es un sólido de revolución generado por el giro de un triángulo rectángulo alrededor de uno de sus catetos: el de su altura. Al círculo formado por el otro cateto —que es el radio—, se le denomina base, y el punto donde confluyen las generatrices es el vértice. De este modo, los elementos del cono son: la altura, el radio, el vértice y la generatriz.
Analizarás cómo cambia el volumen al aumentar o disminuir alguna de sus dimensiones.
¿Qué hacemos?
La fórmula para calcular el volumen de un cono es: volumen es igual al área de la base por la altura entre tres.
¿Te has preguntado por qué se divide entre 3 el área de la base por la altura?
Se divide entre 3 porque tiene relación con el volumen del cilindro.
Tiene relación con el volumen del cilindro porque el volumen del cono es tres veces el volumen de cilindro. Esto, siempre y cuando tengan las mismas medidas la base y la altura.
En el siguiente audiovisual se puntualiza lo anterior, del minuto 03:54 a 07:29.
- Volumen de conos y cilindros
https://www.youtube.com/watch?v=pVDY_dBeLhE
Por lo tanto, la fórmula que se utiliza para el cálculo del volumen de un cono es: volumen es igual a pi por radio al cuadrado, por la altura entre tres.
O bien, dicho de otra manera: volumen del cono es igual al área de la base por la altura entre tres.
Con esta fórmula podrás resolver el tipo de problemas que impliquen el volumen de un sólido de revolución generado cónico.
Revisa la primera situación:
En la escuela de Silvia hay un despachador de agua y para servirse ocupan conos de papel. El diámetro del cono es de 8 cm, y la altura es de 10 cm. ¿Cuál es el volumen del cono?
Los datos que se tienen son:
El diámetro que es = 8 cm
La altura que es = 10 cm
pi, donde utilizarás sólo 3.14 para facilitar operaciones.
Y se sustituyen estos datos en la fórmula para calcular el volumen del cono:
Volumen es igual a pi por radio al cuadrado, por altura, entre 3.
El radio tiene valor de 4, pues es la mitad del diámetro que vale 8.
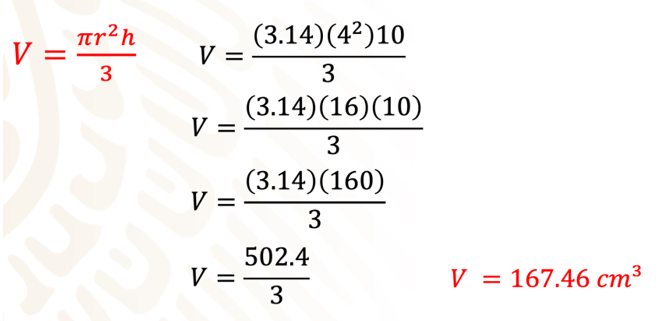
Sustituyendo los datos, se tiene que: volumen es igual a 3.14 por 4 al cuadrado, por 10 entre 3.
Se realizan las operaciones: primero el cuatro, que está elevado al cuadrado, es igual a 16:
16 por 10 es igual a 160, 160 por 3.14 es igual a 502.4, 502.4 entre 3 es igual a 167.46.
Por lo tanto, el volumen del cono es igual a 167.46 cm cúbicos.
Analiza la siguiente situación:

Los datos que conoces son:

Estos son los datos que tienes para resolver el problema. ¿Qué fórmula emplearás?
La fórmula que se utiliza es:
Volumen es igual a pi, por radio al cuadrado, por altura, entre tres. Se sustituyen los valores de los datos en esta fórmula. Volumen es igual a 3.14 por (2) al cuadrado, por 6, entre 3.
El cuadrado de 2 es igual a 4, 3.14 por 4 es igual a 12.56, 12.56 por 6 es igual a 75.36.
Y, por último, 75.36 entre 3, que es igual a 25.12 metros cúbicos.
Te falta multiplicar 25.12 por 7 para saber el total de metros cúbicos que se almacena en todos los silos de don Miguel.
Entonces, ¿cuál es el resultado final?
Multiplicando 25.12, que es el volumen de un silo, por 7 que son en total, es igual a 175.84 metros cúbicos.
25.12 7 = 175.84 m3
Pero a don Miguel no se le acaban los problemas.

Ayuda a don Miguel a resolver este problema.
Lo primero que se hace es saber con qué datos cuentas.
Como es la misma base, el diámetro es de 4 m.
Volumen igual a 30 m cúbicos.
Pi que es 3.14.
La altura es la que desconoces.
Con estos datos, este problema ya se puede resolver.
Pero antes se debe analizar la fórmula, porque ahora calcularás la altura y no el volumen. Entonces, tienes que despejar la altura en la fórmula original.
Volumen es igual a pi por radio al cuadrado, por la altura entre tres.

Se observa que en la fórmula el 3 está dividiendo a pi por radio al cuadrado por la altura. Así que se multiplica por 3 ambos lados de la igualdad y queda 3 por “V” es igual a pi por radio al cuadrado por la altura.
Luego, divide ambos lados de la igualdad por pi por radio al cuadrado, y queda 3 por “V” entre pi por radio al cuadrado, que es igual a la altura.
La fórmula para calcular la altura después de hacer el despeje queda de la siguiente manera:
Altura igual a 3 por el volumen entre el producto de pi, por radio al cuadrado.
Cuando ya tienes la fórmula para calcular la altura, se sustituyen los datos que tienes en la fórmula para calcular la altura, y se realizan las operaciones.
Resuelve el ejercicio en tu cuaderno. Entonces, la fórmula a utilizar es:

Altura es igual a 3 por volumen entre el producto de pi por radio al cuadrado.
Y se sustituyen los valores:
Altura es igual a 3 por 30 entre el producto de 3.14 por 2 al cuadrado
3 por (30) es igual a 90
3.14 por 2 al cuadrado es igual a 12.56
90 entre12.56 es igual a 7.16 m
Por lo tanto, la altura que tiene el nuevo silo es de 7.16 m.
Existe un dulce típico mexicano que tiene la forma geométrica de un cono, estos dulces en forma de cono se llaman chupirules.
Y se les conoce con varios nombres a lo largo del país: chupirul, paragüitas, pico dulce, entre otros. Este caramelo duro es el motivo de la siguiente situación.
Doña Inés, que se dedica a hacer este tipo de dulces para venderlos en las ferias, me pidió que le ayude en algunos cálculos para saber cuánto caramelo se utiliza para cuatro tamaños diferentes: 10, 15, 20 y 25 cm de altura, respectivamente, pero necesita que todos conserven el mismo diámetro de 6 cm.
También quiere saber cuánto caramelo se utiliza si se conserva la altura de 10 cm y varía el diámetro en 4, 8, 12 y 16 cm, respectivamente. Esto le servirá a doña Inés para tomar una mejor decisión para la fabricación de los chupirules.
Lo primero es organizar los datos que se presentan y puedes hacerlo en tablas para después realizar los cálculos.
Se comienza a calcular el área de la base de cada uno de los dulces.
Comienza por encontrar el área de la base, y para ello multiplica pi por el radio al cuadrado.
Se sustituyen los valores para la medida 1. Tienes: Área de la base es igual a 3.14 por 3 al cuadrado.
Por lo tanto: Área de la base es igual 28.26 cm cuadrados.
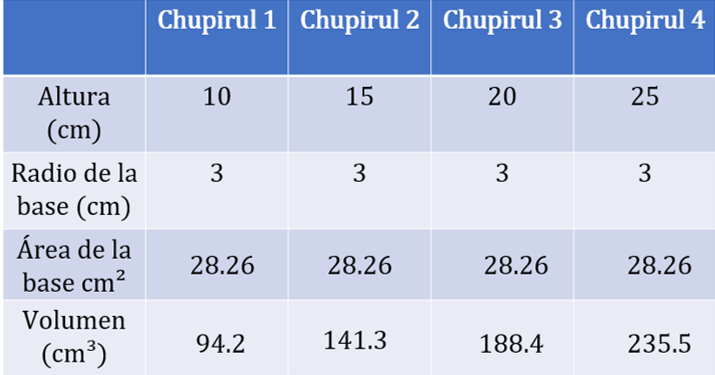
Ya que se tiene que el área de la base para todos los tamaños del chupirul, y que es la misma, se sustituyen en la fórmula para calcular el volumen de cada uno de los tamaños.
28.26 por 10 entre 3 es igual a 94.2 cm cúbicos
28.26 por 15 entre 3 es igual a 141.3 cm cúbicos
28.26 por 20 entre 3 es igual a 188.4 cm cúbicos
Y 28.26 por 25 entre 3 es igual a 235.5 cm cúbicos
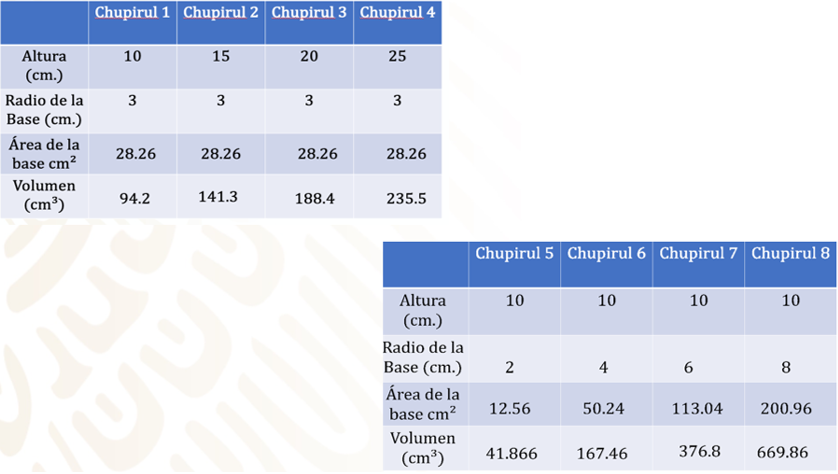
Se tiene la primera tabla del volumen de caramelo que se va a utilizar para cada chupirul, y como se conserva el diámetro, lo que varía es la altura de cada uno.
Después, se calcula el área de la base variando el valor del radio, en 2, 4, 6 y 8 cm, respectivamente. Es indispensable la tabla para llevar en orden los datos.
Sustituye estos valores en la fórmula para calcular el área de la base.
3.14 por 2 al cuadrado es igual a 12.56 cm cuadrados
3.14 por 4 al cuadrado es igual a 50.24 cm cuadrados
3.14 por 6 al cuadrado es igual a 113.04 cm cuadrados
3.14 por 8 al cuadrado es igual a 200.96 cm cuadrados
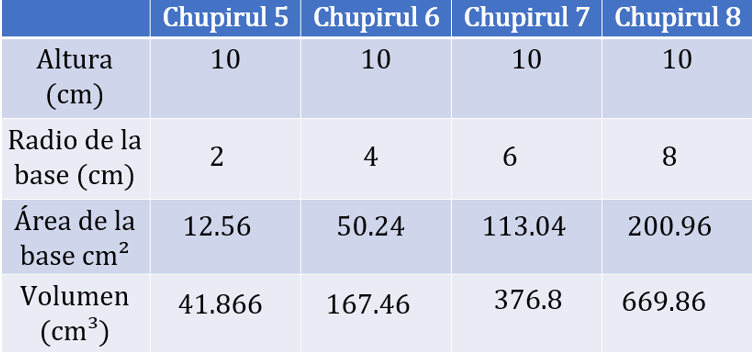
Se sustituyen estas áreas en la fórmula para calcular el volumen de cada dulce, conservando el valor de la altura, que para todos es de 10 cm.
Se sustituyen las áreas de las bases calculadas en la fórmula para calcular el volumen.
12.56 por 10 entre 3 es igual a 41.866 cm cúbicos.
50.26 por 10 entre 3 es igual a 167.46 cm cúbicos.
113.04 por 10 entre 3 es igual a 376.8 cm cúbicos.
200.96 por 10 entre 3 es igual a 669.86 cm cúbicos.
Por último, se analizan las tablas para saber qué sucede con el volumen cuando la altura y el radio varían.
¿Qué se observa en las tablas con relación al volumen?, ¿cómo te imaginas los cuerpos de los dulces cuando se van modificando sus medidas?
Observando los valores 1, 2, 3 y 4 son delgados y largos, porque la altura es variable y su radio es constante.
En cambio, los dulces 5, 6, 7 y 8 son cortos y de mayor grosor, porque su altura permanece constante y al variar el radio adquiere valores más grandes.
Esa es una apreciación muy general. Debes analizar los datos obtenidos cuando la altura de los dulces varió y el radio permaneció constante.
Cuando el radio de 3 cm fue constante en todos los conos, se observó que, si la altura varía, por ejemplo, al doble como en el caso de una altura de 10 y 20 cm, el volumen se duplicó. Se tenían 94.2 cm cúbicos en el primero y 188.4 cm cúbicos en el de 20 cm de altura.
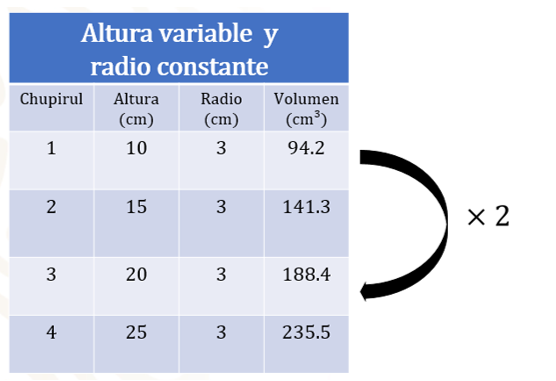
Se observa que existe una variación en el volumen cuando se modifica la altura o el radio. Es decir, en los dulces 1, 2, 3 y 4 aumenta de manera lineal porque el radio permanece constante, y sólo se multiplica por una cantidad “x”.
Se observa a continuación la tabla cuando lo que cambió en los dulces fue el radio de la base.
En ella fue posible notar que, si se duplica el radio, el volumen aumenta 4 veces.
Si el radio se triplica, como el caso del dulce 5 con respecto al 7, el volumen aumenta 9 veces.
Y si el radio aumenta 4 veces, como en el caso de los chupirules 5 y 8, el volumen aumenta 16 veces.

¿Y a qué se debe esta situación?
La explicación está en que la dimensión del radio en la fórmula que calcula el área de un círculo está elevada al cuadrado. Eso permite que el volumen se vea afectado en esa relación.
Esto es más claro en la gráfica que se genera con los datos del radio y del volumen de cada cono. Como se observa, es una curva que representa una relación cuadrática.
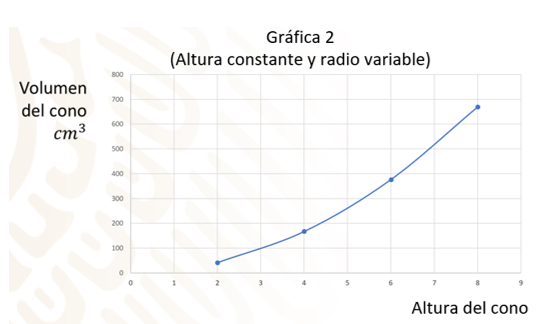
Se resalta que las gráficas indican la variación del volumen de los conos al mantener la medida del radio o de la altura.
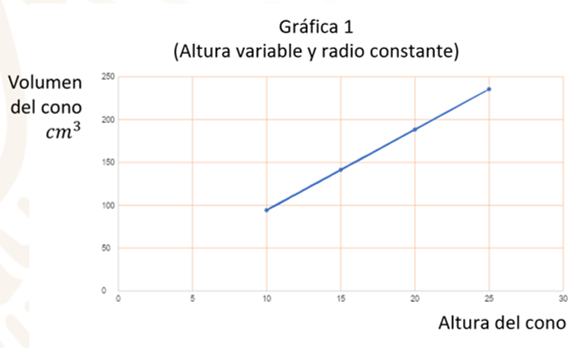
La gráfica 1 es una línea recta porque si la medida de su radio se mantiene constante, se establece una relación de proporcionalidad entre la medida de la altura y la medida de su volumen.
La gráfica 2 es una curva porque si la medida de su altura se mantiene constante, se establece una relación cuadrática entre la medida del radio y la medida de su volumen.
Y de este modo, se estudia el resultado de cambiar una de las dimensiones de un cono.
Estos ejemplos le dan significado a los posibles cambios que se pueden tener en el volumen del cono. Conociendo esto, puedes anticipar lo que sucede al variar una u otra de las dimensiones de un cuerpo geométrico.
El reto de hoy:
Consulta tu libro de texto para fortalecer este contenido.
Con las notas que escribiste en tu cuaderno, construye ejercicios para practicar más sobre el volumen en un sólido de revolución cónico.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas