Volumen de prismas y del cilindro recto
Volumen de prismas y del cilindro recto
Aprendizaje esperado: resuelve problemas que implican calcular el volumen de cilindros y conos o cualquiera de las variables que intervienen en las fórmulas que se utilicen. Anticipa cómo cambia el volumen al aumentar o disminuir alguna de las dimensiones.
Énfasis: dar sentido y significado a la variación de alguna de las dimensiones del volumen en prismas y cilindros.
¿Qué vamos a aprender?
Estudiarás el cálculo del volumen de prismas con diferentes bases y el cilindro recto para conocer qué ocurre con el volumen al aumentar o disminuir algunas dimensiones de los cuerpos geométricos.
Los materiales que vas a utilizar es tu cuaderno de apuntes, bolígrafo, lápiz y goma.
Anota en tu cuaderno los apuntes que consideres necesarios.
Los cuerpos geométricos están presentes en la vida diaria: desde el recipiente que contiene la leche o el empaque de un chocolate; en las botellas de múltiples productos o los envases para guardar los alimentos.
También los cuerpos geométricos se emplean para contener petróleo y gas; en los electrodomésticos y hasta en las albercas.
Como puedes observar, hay una gran variedad y todos ellos comparten ciertas características, además de fórmulas para calcular su capacidad o volumen.
Estas fórmulas permiten anticipar cómo cambia su volumen al transformar sus dimensiones.
¿Qué hacemos?
Comienza con los prismas.
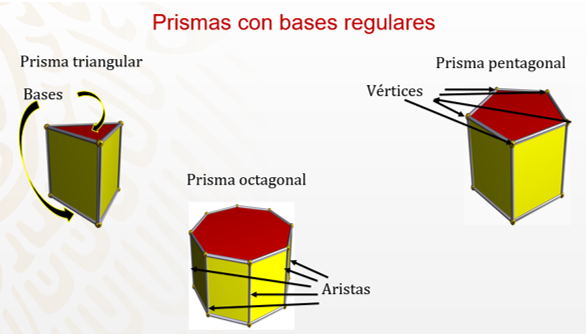
El nombre de un prisma se asigna por la figura que tienen sus bases.
Si sus bases son triángulos, se trata de un prisma triangular. Pero si su base tiene 5 vértices, se trata de un prisma pentagonal. O si se habla de un prisma que lo forman 8 aristas laterales, es un prisma octagonal.
Cuando sus bases son círculos y su cara lateral es un rectángulo, entonces el cuerpo geométrico es un cilindro.
Realiza la siguiente actividad.
Imagina el cuerpo geométrico que se te describe con las siguientes características. Esto para comparar las respuestas y saber si se habla del mismo.
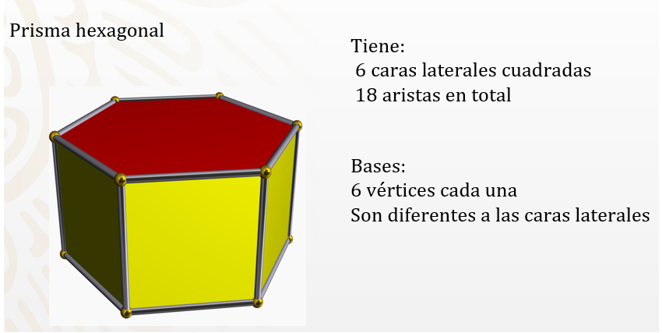
Tiene 6 caras cuadradas, pero no se trata de un cubo que tiene 6 caras iguales. Tiene 18 aristas en total. Las bases son diferentes a las caras laterales. Y cada base tiene 6 vértices. ¿Qué cuerpo geométrico es? ¿Con cuántas pistas identificaste el cuerpo geométrico?
Si tu respuesta fue un prisma hexagonal, estás en lo correcto: tiene 6 caras laterales cuadradas, 18 aristas en total; sus bases tienen 6 vértices cada una y las bases son diferentes a las caras laterales.
Antes de empezar con el cálculo del volumen, ¿sabías que a sus unidades de volumen se les llama cúbicas?
Esto es porque al partir de un cubo en donde sus tres dimensiones son iguales tanto largo, ancho y alto, al multiplicarlas se obtiene: lado por lado por lado, igual a lado a la tercera potencia, es decir, lado al cubo.
Por lo tanto, a las unidades que se usan en el volumen se les denomina cúbicas, como metro cúbico, decímetro cúbico, centímetro cúbico, entre otras.
Ahora, considera una caja de galletas con forma de prisma rectangular. De ésta se quiere calcular su volumen y sus dimensiones son las siguientes:
De largo mide cuatro unidades, de ancho tres unidades y de alto dos unidades.
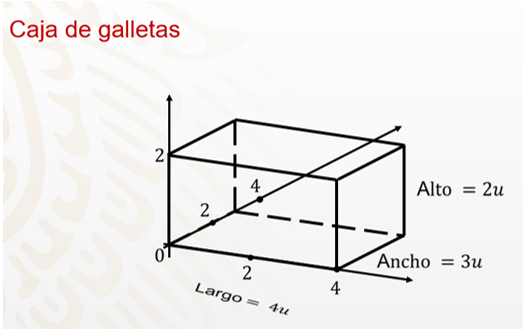
Calcula el número de cubos que caben en la base del prisma. Por ejemplo, si acomodas 4 de largo en 3 hileras —que es lo que mide de ancho el prisma—, y obtienes en la base 12 cubos.
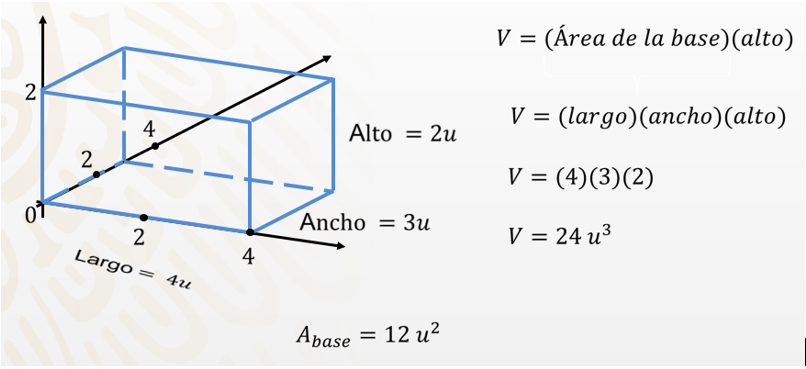
Repite este procedimiento una vez más porque tiene una altura de 2 unidades, entonces se sostiene que el volumen de esta caja de galletas es de 24 unidades cúbicas.
Se concluye numéricamente que el volumen es igual al producto del área de la base por la altura. Es decir, largo por ancho por alto, que es igual a 4 por 3 por 2 igual a 24 unidades cúbicas.
Así se comprueba que, en ambos casos, el cálculo del volumen es igual.
Ahora analiza qué ocurre con el volumen de este prisma, si la altura de la caja de galletas fuera mayor.
Si partes de la fórmula de volumen —que es área de la base por altura—, y conoces que el área de la base se mantiene en 12 unidades cuadradas. ¿Cuál es el volumen de una caja con una altura del doble? Es decir, de 4 unidades y otra caja con una altura de 12 unidades.
Se parte de la fórmula del volumen del prisma —que es igual al área de la base por altura—, igual a 12 por cada una de las nuevas alturas, es decir, 12 por 4 que es igual a 48 unidades cúbicas.
Para la siguiente caja, el volumen es igual a 12 por 12, igual a 144 unidades cúbicas.
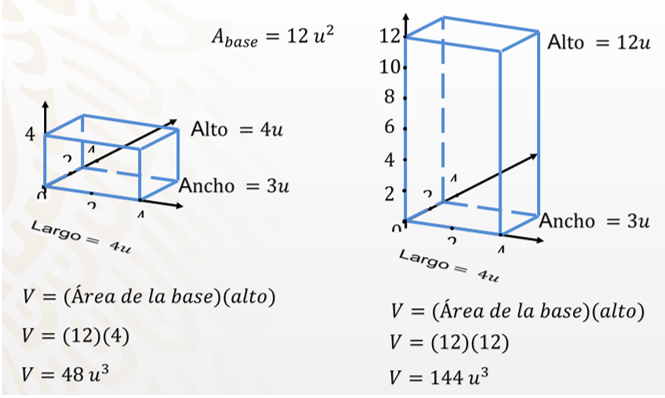
¿Observaste algún patrón en los resultados del volumen? Analiza:
Se tienen las tres cajas con la misma base y sólo cambia la altura. Por lo tanto, si la altura de la segunda caja aumentó el doble de la primera, el volumen también aumenta de 24 a 48 unidades cúbicas, el doble.
En el segundo caso, se observa que la altura aumentó seis veces la del original. Por lo tanto, el volumen también se modificó 6 veces, es decir, 24 por 6 que son 144 unidades cúbicas.
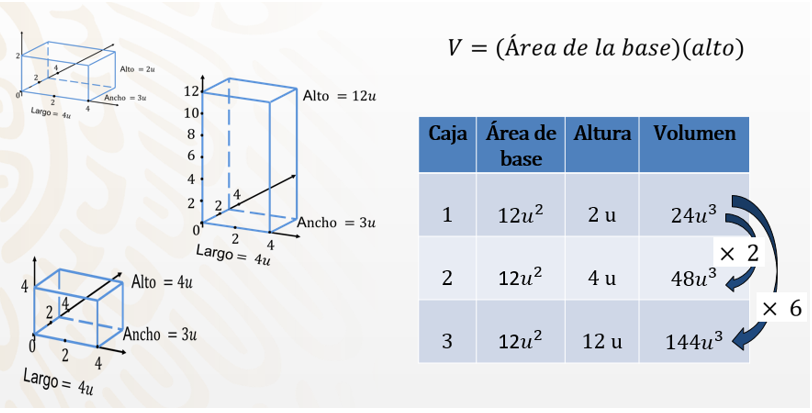
Al analizar la tabla, se observa una constante que es el área de la base. Para estos tres cuerpos geométricos, sólo cambias una de sus dimensiones que es la altura.
Hasta aquí ya calculaste el volumen para un prisma rectangular con variables de una dimensión, como la altura.
Pero ¿qué ocurre con los prismas que tienen otra figura como base? ¿Se cambia la fórmula para calcular el volumen si tienes otro tipo de base? ¿Qué pasa si la base ahora es un círculo?
Para contestar estas preguntas, en el siguiente video del minuto 02:05 al 03:52 se muestran prismas con diferentes figuras en la base, hasta llegar al cilindro.
- Volumen de conos y cilindro
https://www.youtube.com/watch?v=pVDY_dBeLhE
Se puede concluir que, para calcular el volumen de cualquier prisma y cilindro, sólo debes multiplicar el área de la base por la altura.
Ahora continua con la actividad 2.
Se quiere conocer el volumen que contiene una caja de chocolate con forma de prisma hexagonal con una altura de 12 cm, de radio 4 cm y una apotema de 3.4 cm.
¿Cómo calcularías el volumen?
Primero se calcula el área de la base. Al ser un hexágono, el área es igual al perímetro por apotema sobre 2.
Entonces, el perímetro que es igual al lado por 6 —por tratarse de un hexágono—, el radio y el lado tienen el mismo valor. Por lo tanto, 6 por 4 es igual a 24 cm.
Ahora, el área es igual a 24 por 3.4 sobre 2, igual a 81.6 entre 2, igual a 40.8 cm cuadrados.
El volumen es igual a 40.8 por 12, igual a 489.6 cm cúbicos.

Si se analizan los dos problemas, el cálculo requirió otros elementos porque las bases son diferentes y la fórmula del área cambia. Después de ese cálculo sólo hay que multiplicar por la altura.
Si el fabricante indica que cada tablilla que contiene la caja tiene una altura de 1 cm.
¿Qué volumen tendrá una caja con 4 tablillas, 6 tablillas y la edición especial de 20 tablillas?
Completa la actividad, ayudando al fabricante a calcular el volumen de estas presentaciones.
Para facilitar los cálculos, se traza una tabla, no sin antes considerar que el área de la base es la misma para todas las presentaciones. Por lo tanto, ese valor es constante, y se multiplica por las alturas solicitadas.
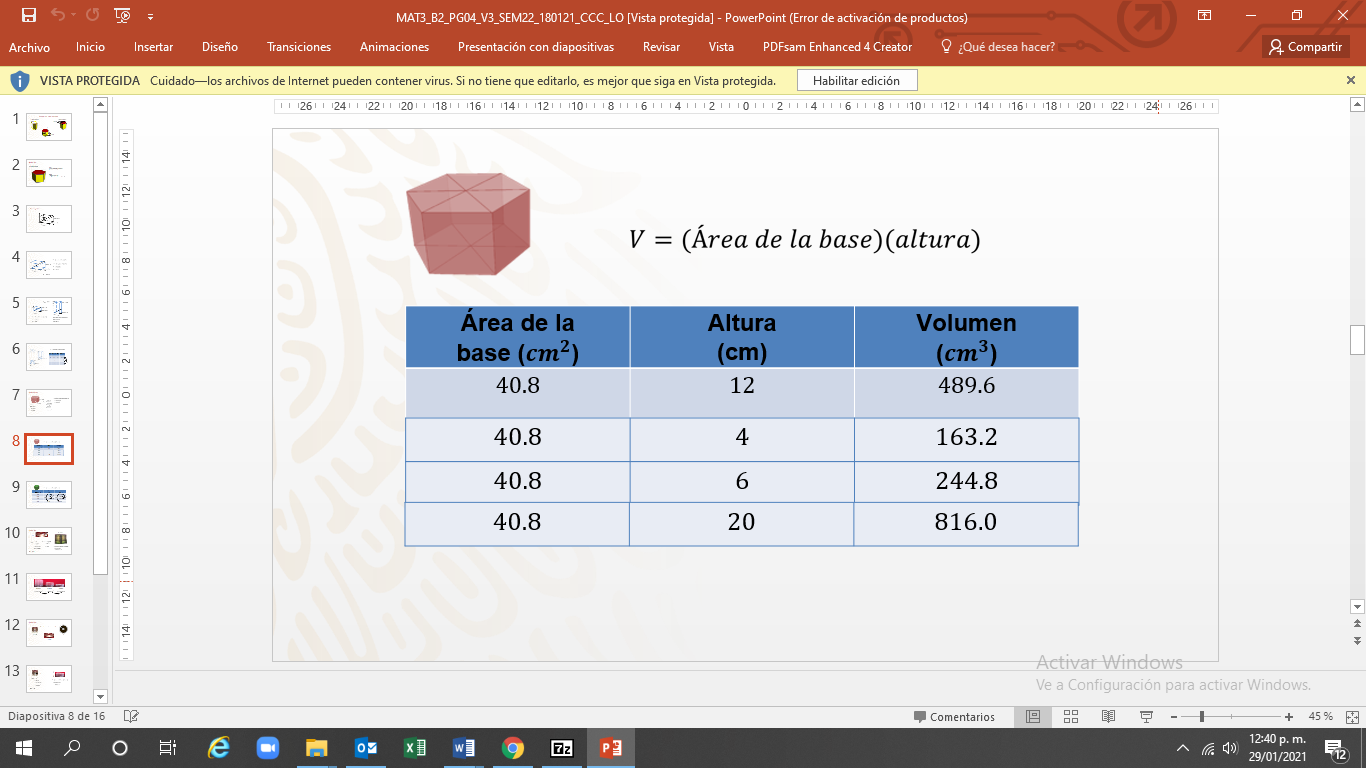
Para la caja de 4 tablillas se multiplica 40.8 por 4, igual a 163.2 cm cúbicos. Para la segunda presentación se multiplica 40.8 por 6, igual a 244.8 cm cúbicos. Para la edición especial se multiplica 40.8 por 20, igual a 816 cm cúbicos.
Conociendo el área de la base, para calcular el volumen sólo se multiplica el área por la altura solicitada, pero no es la única forma de realizarlo.
Si conoces el volumen del prisma, es posible calcular el de las nuevas presentaciones, a través de determinar la relación entre las alturas.
Se revisas los datos de la tabla anterior para realizar ahora los cálculos, partiendo del volumen que tenía una altura de 12 cm.
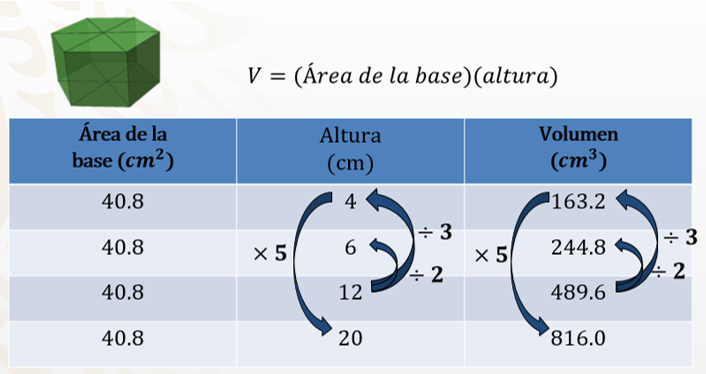
Si la primera altura solicitada representa la tercera parte del original, entonces se divide el volumen original de 489.6 entre 3, que es igual a 163.2 cm cúbicos.
Para la segunda altura observas que es la mitad de la primera. Por lo tanto, se divide 489.6 entre 2, igual a 244.8 cm cúbicos.
En la edición especial se observa que la altura es mayor a la altura original y no es múltiplo de ella. Pero el 20 —al ser múltiplo de 4, ya que 4 por 5 es 20—, se puede multiplicar al volumen de la altura de 4 que es 163.2 por 5, teniendo 816 cm cúbicos.
En las dos tablas se obtiene el mismo valor del volumen.
Se concluye que es directamente proporcional la altura con el volumen, siempre y cuando la base no se modifique.
Ahora analizarás qué pasa con el cilindro.
Tienes un contenedor para discos que tiene una capacidad para 60 piezas. Cada disco mide 6 cm de radio y 1.5 mm de alto.
¿Cuál es el volumen del contenedor?
Si tienes dos contenedores de 30 y 10 discos, ¿cuál es el volumen de éstos?
Para calcular el volumen del cilindro, primero se debe conocer el área de la base, y por ser un círculo, su fórmula es pi por radio al cuadrado.

Se sustituye el valor del radio, 6 cm, y se eleva al cuadrado para obtener 36. Lo multiplicas por 3.14 y obtienes 113.04 cm al cuadrado.
En la altura se tienen 60 discos de 1.5 mm, que es igual a 90 mm y equivalen a 9 cm para manejar todo en cm.
Multiplicas el área de 113.04 por 9 de altura, y da 1 017.36 cm cúbicos, como volumen del contenedor.
Después, se sigue con el mismo procedimiento de multiplicar el área de la base por la altura.
Se tienen otros contenedores de 30 y 10 discos, ¿cuál es su volumen?
Se conoce el volumen del contenedor mayor, que mide 1 017.36 cm cúbicos, con una altura de 60 discos. Se calcula el volumen del segundo contenedor con 30 discos, siguiendo el razonamiento que trabajaste con el prisma. Al ser la mitad de la altura, se divide el volumen entre 2 porque se conserva la misma base, y obtener 508.68 cm cúbicos.

Para el contenedor con 10 discos realizas la división del volumen, partiendo del segundo contenedor, el cual es la tercera parte. Se divide 508.68 entre 3, igual a 169.56 cm cúbicos.
Como “dato relevante”: en el caso del cilindro, también existe una relación de proporcionalidad directa entre la altura del cilindro y el volumen, siempre y cuando tengan la misma medida en la base.
Sólo te falta por analizar: ¿qué pasa con el volumen si la medida de la base cambia? ¿Se mantendrá la misma relación de proporcionalidad?
Analiza estas preguntas con la cuarta y última actividad.
Continúa trabajando con tus contenedores de discos, pero ahora cambia el diámetro del disco, ya que algunos son contenedores para disco de cámara de video, discos para computadora o para discos de vinilo.
¿Cuál es el volumen de los tres contenedores, si se quieren almacenar tres grupos de discos con una altura de 10cm?
¿Qué relación existe entre el volumen y la variación de la base?
En esta actividad se tienen los siguientes datos: la altura de los tres contenedores es la misma de 10 cm; el radio de cada disco es el que cambia. En el disco para cámara de video, su radio mide 3 cm. El disco para computadora tiene un radio de 6 cm. Y el disco de vinilo grande tiene un radio de 15 cm.
Con estos datos se calcula el volumen de los contenedores.
Para el primer contenedor se calcula el área de la base que es pi por radio al cuadrado. Se sustituye para tener pi por 3 al cuadrado, igual a 3.14 por 9, igual a 28.26 cm cuadrados.
Para el volumen del cilindro se multiplica el área de la base por altura, que es 28.26 por 10 igual a 282.6 cm cúbicos.

Ahora realiza el cálculo para el segundo contenedor.
Para el segundo contenedor, el área de la base es igual a pi por 6 al cuadrado, igual a 3.14 por 36, igual a 113.04 cm cuadrados.
Su volumen es: área de la base por altura, igual a 113.04 por 10 igual a 1 130.4 cm cúbicos.
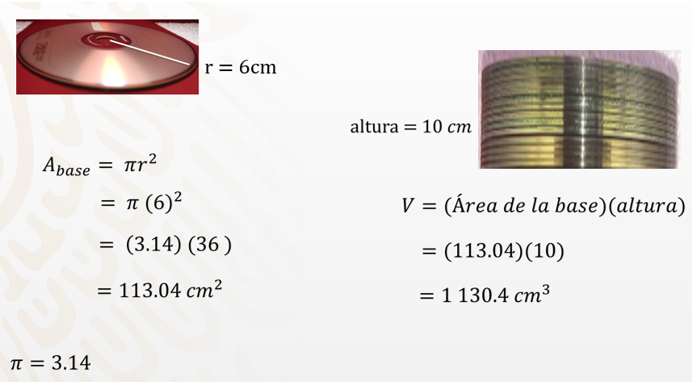
Ahora sólo falta el cálculo del tercer contenedor, de radio igual a 15 cm.
Este es el contenedor más grande, cuya área de la base es igual a pi por 15 al cuadrado, igual a 3.14 por 225, igual a 706.5 cm cuadrados.
Su volumen es área de la base por altura, igual a 706.5 por 10 igual a 7 065 cm cúbicos.

Ya se realizó el cálculo del volumen de los tres contenedores, el cual fue aumentando conforme aumentó el radio del disco.
Ahora, sólo falta analizar la segunda pregunta, que dice: ¿qué relación existe entre el volumen y la variación de la base?
Para ello, se inserta la información en una tabla.
En la tabla observas que la altura de los contenedores se mantiene constante, y que tanto el valor de los radios como el área de la base y el volumen aumentaron.
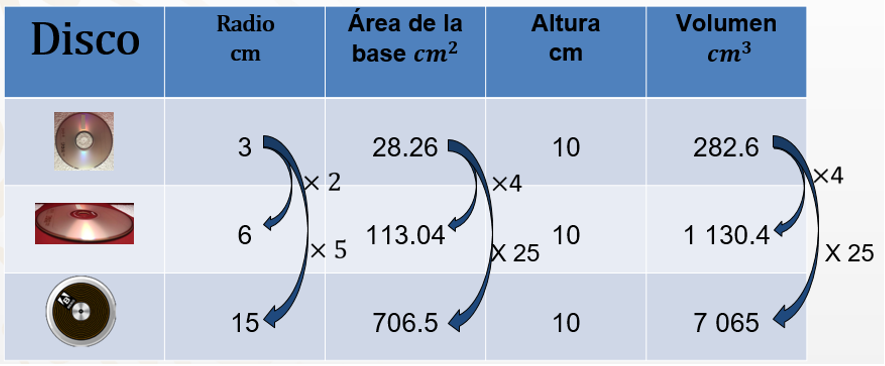
Del primer disco al segundo, el aumento del radio es al doble. El área de su base se hizo 4 veces mayor por el efecto de elevar al cuadrado el radio. Al ser la altura una constante en ambos, el volumen entonces es 4 veces mayor.
Es decir, 2 al cuadrado es 4; 28.26 por 4 es 113.04 y en el caso del volumen, al multiplicar 282.6 por 4, es 1 130.4 cm cúbicos.
Al comparar el primer disco con el tercero, se observa que el radio es 5 veces mayor. Con la consideración anterior —que el radio aumenta al cuadrado—, tienes 5 al cuadrado es 25. Por lo que el área de la base es 25 veces mayor.
Se comprueba: el área de 28.26 del primer disco por 25 es igual a 706.5, y en el volumen es 282.6 por 25, igual a 7 065 cm cúbicos.
Otro “dato relevante”: la relación entre el radio y el volumen final no es directamente proporcional —porque el radio es elevado al cuadrado para obtener el área de la base—por lo que si las dimensiones de la base se duplican, y la altura se conserva constante, el volumen será 4 veces mayor.
Si el radio se triplica, y la altura del cilindro es constante, el volumen será 9 veces mayor.
En conclusión: con una altura constante y un radio que aumenta proporcionalmente, el volumen aumenta un número de veces equivalente al cuadrado del aumento del radio.
Con las cuatro actividades se analizó el cálculo del volumen en prismas y cilindros, que, de modo general, se obtiene multiplicando el área de la base por la altura.
Con la particularidad de que el área de la base depende de la figura geométrica que corresponda.
También se analizó el cambio del volumen al aumentar o disminuir una dimensión del cuerpo geométrico, como la altura que tiene una relación de proporcionalidad directa con el volumen, conservando la misma base.
Mientras que cuando cambia el área de la base, que tiene dos dimensiones (largo y ancho), por ejemplo, el radio de un cilindro, el número de veces que es mayor que otro, se eleva al cuadrado para saber cuántas veces el volumen se incrementa, siempre y cuando la altura sea constante.
El reto de hoy:
Busca en tu libro de texto todo lo relacionado con este tema, y resuelve los ejercicios que ahí se proponen. De esta forma enriquecerás tu conocimiento.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas
