Volumen de prismas rectos II
Volumen de prismas rectos II
Aprendizaje esperado: calcula el volumen de prismas y cilindros rectos.
Énfasis: dar sentido y significado al cálculo del volumen de prismas rectos.
¿Qué vamos a aprender?
“La filosofía está escrita en ese grandísimo libro abierto ante los ojos; quiero decir, el universo, pero no se puede entender si antes no se aprende a entender la lengua, a conocer los caracteres en los que está escrito. Está escrito en lengua matemática y sus caracteres son triángulos, círculos y otras figuras geométricas, sin las cuales es imposible entender ni una palabra; sin ellos es como girar vanamente en un oscuro laberinto”; esta fue una frase de Galileo Galilei e ilustra muy bien lo que estudiarás en esta sesión, ya que seguirás profundizando en el lenguaje de la geometría. Para ello, retomarás los desarrollos planos de algunos prismas.
¿Qué hacemos?
Cuando se planea producir un artículo, cómo las cajas para guardar algún regalo, a la par del trabajo de los diseñadores gráficos que realizan el desarrollo plano de la caja, también se realiza una planeación de materiales, costos de producción y capacidad para almacenar el producto.
En esta ocasión, calcularás cuánto material se necesita para construir los desarrollos planos y cuánto lugar ocuparán para ser almacenados. Así que analiza la primera situación.
Una persona solicitó una caja para guardar un anillo. Tenemos el desarrollo plano de la caja formado por 6 cuadrados, que se muestra a un lado y sobre la que se marcó sólo una medida, la cual es de 5 centímetros.

Tomando como base el desarrollo plano que se muestra, ¿será posible construir una caja conociendo sólo la medida señalada?, ¿qué volumen tiene la caja armada?
Analiza unos segundos las preguntas y anota tus respuestas. Para que luego las puedas comparar.
Seguramente ya te diste cuenta que sí es posible construir la caja teniendo sólo una medida, ya que, al tener todas sus caras cuadradas, se trata de un cubo y todos sus lados miden lo mismo. Sabiendo esto, responde la siguiente pregunta, ¿qué volumen tiene la caja armada?
En la imagen se muestra la caja y las medidas de sus aristas, que en todos los casos es la misma.

Una manera de calcular el volumen de la caja para el anillo es a través de la fórmula volumen igual a área de la base por altura. Podemos comenzar obteniendo el área de la base. En este caso es una base cuadrangular, por lo que se puede utilizar la fórmula área igual a lado por lado.
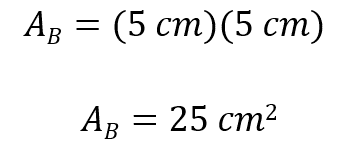
Una vez obtenida el área de la base, la sustituimos en la fórmula del volumen y tenemos que:
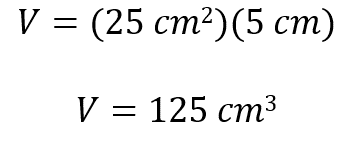
El volumen de la caja es igual a 125 centímetros cúbicos. Por lo tanto, ese es el espacio que ocupa la caja al ser armada.
Ahora han solicitado elaborar una caja en forma de cubo de 25 centímetros por lado. ¿Cambiará la forma de obtener su volumen?

La forma para obtener el volumen será la misma, es decir, multiplicar el área de la base por la altura. Entonces, área de la base es igual a lado por lado; al sustituir, tenemos.
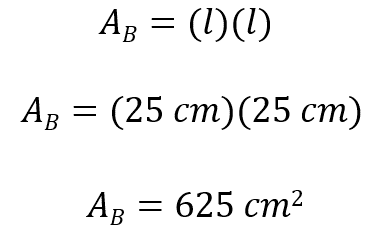
Su altura es igual a 25 centímetros, misma que multiplicaremos por el área de la base para determinar el volumen.
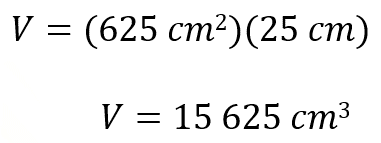
El volumen es igual a 15 625 centímetros cúbicos. Que representan el espacio que ocupa la caja, o su volumen.
La empresa que fabrica las cajas en forma de prisma triangular para guardar los chocolates, también desea saber cuánto espacio ocuparán las cajas, como la de la imagen, al ser armadas.

Debido a que es un prisma triangular, necesitamos saber la longitud del lado del triángulo y la altura para esa base del mismo triángulo, así como la altura del prisma.

Si sabemos la medida del lado del triángulo, señalada con azul, mide 4 centímetros y su altura es de 3.46 centímetros; ¿cuál es la altura del prisma si su volumen es de 103.8 centímetros cúbicos?
Para resolver este problema, sólo conocemos las medidas del lado de la base del triángulo, la altura del mismo triángulo y el volumen de la caja al ser armada.
Por otro lado, sabemos que el volumen de la caja es igual al área de la base del prisma por la altura del prisma. Al analizar los datos te puedes dar cuenta que el área de la base del prisma, que es un triángulo, se puede calcular usando la fórmula área de un triángulo.
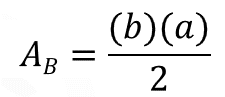
Entonces, el volumen del prisma triangular se puede expresar como base del triángulo por altura del triángulo “a” entre dos, por altura del prisma.
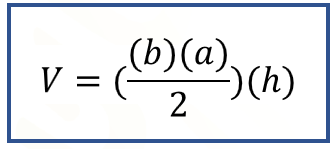
Al sustituir los datos, tenemos.
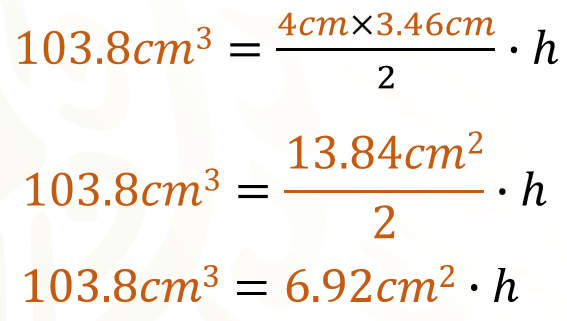
Despejamos la altura del prisma y determinamos que.

El valor de la altura del prisma es igual a 15 centímetros.
Continua con una caja para tostadas, como la que se muestra.

Al tratarse de un prisma, la fórmula para calcular su volumen es área de la base por altura.
Se requiere saber el área de la base. Como la base es un hexágono, su área se puede calcular con la fórmula.
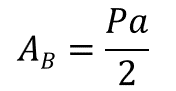
Para determinar su perímetro podemos utilizar la medida de uno de sus lados. Supongamos que esta longitud es de 7.5 centímetros. Para utilizar la fórmula del área, se requiere conocer la medida de la apotema, que supongamos que no la conocemos, entonces apotema es igual a “x”. Por otro lado, se requiere la medida de la altura del prisma. En este caso, supongamos que mide 20 centímetros. Ahora, si el volumen es igual a 2,925 centímetros cúbicos, ¿cuál es el valor de la apotema?
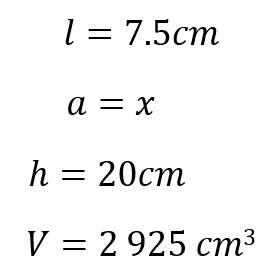
Para conocer el valor de la apotema debemos sustituir los datos en la fórmula. Aunque no conocemos el perímetro, podemos calcularlo multiplicando 7 punto 5 por los 6 lados de la base hexagonal. Por lo que, al sustituir en la fórmula tenemos.
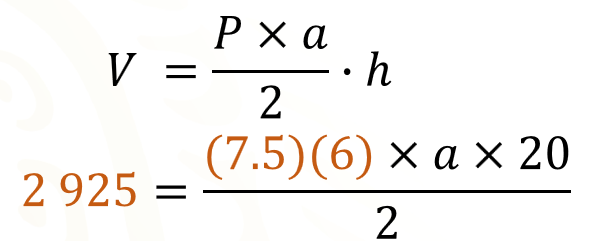
Para despejar la apotema, podemos comenzar multiplicando ambos miembros de la igualdad por 2.
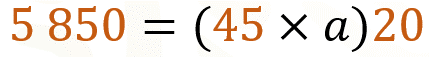
Podemos continuar dividiendo ambos miembros entre 20.
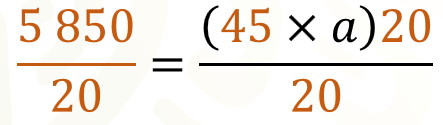
Al resolver, queda.
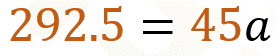
Posteriormente dividimos ambos lados de la igualdad entre 45.

Con ello hemos encontrado su valor, el cual es 6.5, que en el contexto del problema significa que la apotema mide 6.5 centímetros.
Pero si la empresa también desea tener una caja en la cual se vendieran la mitad de las tostadas que contiene el empaque del cual acabas de calcular su apotema, ¿qué piensas que se puede hacer calcular las medidas de esta nueva caja?

¿Qué debemos modificar en el empaque si queremos vender la mitad de las tostadas, sin que las tostadas modifiquen su tamaño?
Aunque las respuestas pueden ser varias, lo más práctico es reducir la altura del empaque a la mitad.
Como la altura del empaque original es de 20 centímetros, la nueva altura del empaque será de 10 centímetros. Sustituye en la fórmula para calcular el volumen y comprobar que, efectivamente, el volumen de esta caja es la mitad que el volumen del empaque anterior.
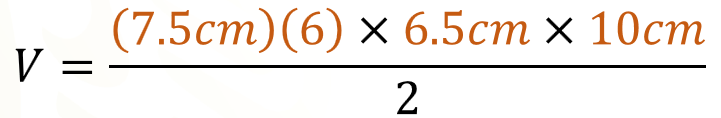
Recuerda que ahora sustituimos 10 en la altura, porque es la mitad de la altura del prisma original.
Al realizar la multiplicación de los factores del numerador, obtenemos 2 925 cm cúbicos, lo que hay que dividir entre 2 para determinar el volumen.
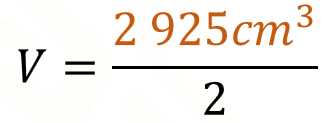
Al resolver esta división obtenemos.
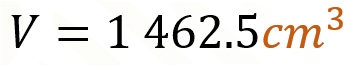
Este resultado es, efectivamente, la mitad del volumen del empaque anterior, de esta forma tenemos un empaque sin modificar el tamaño de las tostadas.
Ahora considera un empaque de pañuelos desechables. Supón que se conoce la altura del prisma que es igual a 5.5 centímetros y también se conoce el ancho de la base, que es igual a 11.5 centímetros, así como el volumen del mismo, el cual es de 1,549.625 centímetros cúbicos. No conocemos el largo de la base del prisma.
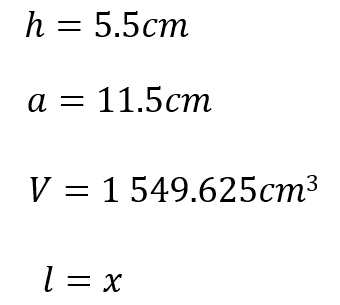
Uno de los caminos para calcularlo es sustituir en la fórmula que has usado para calcular el volumen de un prisma y despejar la incógnita, que representa el largo de la base del prisma. Como el prisma tiene base rectangular, entonces calculamos su área multiplicando la longitud del ancho por la longitud del largo, teniendo en cuenta que este último es el dato desconocido.
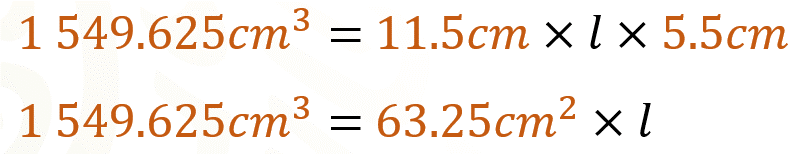
Para despejar el largo de la base, y con ello obtener su valor, dividimos ambos miembros de la ecuación entre 63.25 cm cuadrados.
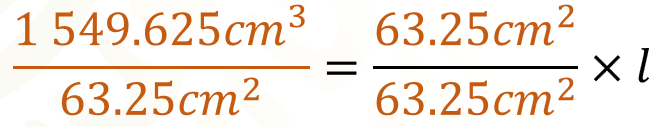
Obteniendo con ello.

Lo cual, en el contexto del problema significa que el largo de la base de la caja de pañuelos mide 24.5 centímetros.
Ahora observa el siguiente video para saber cómo calculan el volumen de un prisma parecido al que trabajaste. Identifica si hay diferencias en el procedimiento ahí mostrado y lo que has realizado.
- Volumen de prismas
https://www.youtube.com/watch?v=64weeCZL3yc
Recuerda que este es un material de apoyo y que, para complementar lo estudiado, puedes consultar otras fuentes, como tu libro de texto de Matemáticas de segundo grado.
El reto de hoy:
Te invitamos a que retomes la última consigna del video, “comentar en qué casos de la vida cotidiana has tenido que calcular el volumen de un prisma”, y para ello; busca en tu casa los prismas que puedas encontrar. Dibújalos en tu cuaderno y coloca en los dibujos, las medidas necesarias para calcular su volumen.

Seguramente podrás encontrar muchos más, por ejemplo, en la caja del cereal o en algún empaque de galletas.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa.
Para saber más:
Lecturas