Volumen de cilindros I
Volumen de cilindros I
Aprendizaje esperado: calcula el volumen de prismas y cilindros rectos.
Énfasis: dar sentido y significado al cálculo del volumen de cilindros rectos.
¿Qué vamos a aprender?
En esta sesión resolverás problemas para dar sentido y significado al cálculo del volumen de cilindros rectos.
¿Qué hacemos?
Para comenzar, lee el siguiente problema.
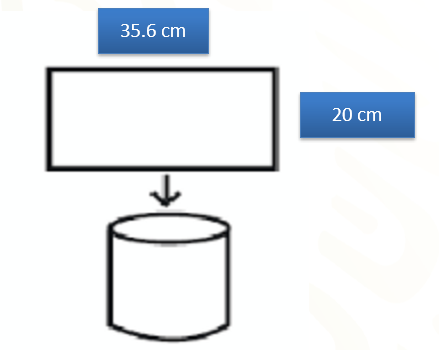
Para construir dos dulceros se requieren dos tubos. Para armar los tubos, se tienen dos láminas de cartulina en forma rectangular de 35.6 centímetros de largo por 20 centímetros de ancho. Uno de los tubos se construye al pegar los lados más cortos de una de las láminas rectangulares. El otro tubo se construye al pegar los lados más largos de la otra lámina rectangular. ¿Cuál de los dos tubos ocupa mayor espacio?
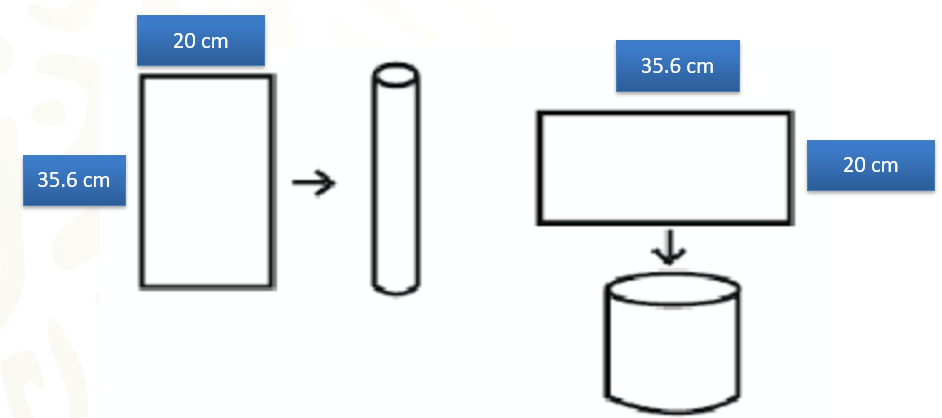
Toma dos hojas que ya no utilices y construye los dos tubos como se instruye en el problema. Puedes ocupar hojas con diferente tamaño del que se indica en el problema, aunque es importante que esas dos hojas sean iguales entre sí. La construcción es para que experimentes y pienses en la resolución del problema.
Toma un momento para construir los dos tubos. Observa los tubos que construiste y piensa en una respuesta al problema.
Al preguntarle a algunos estudiantes, se obtuvieron respuestas distintas al problema. Analiza cada una y elije la que consideres correcta.
El equipo 1 mencionó que los dos tubos estaban hechos con rectángulos de las mismas medidas y que, por tanto, ambos tubos debían ocupar el mismo espacio.
El equipo 2 construyó los tubos y, al observarlos, se dio cuenta de que uno era más alto que el otro. Con base en esta observación, concluyó que el tubo más alto debía ocupar mayor espacio.
El equipo 3 construyó los tubos y, para cada uno, tomó la medida de la distancia perpendicular entre las dos bases. Luego calculó el área de la base de cada tubo. Después de algunos cálculos, concluyó que el tubo más bajo ocupa mayor espacio.
Anota en tu cuaderno la opción que consideres correcta y justifícala.
Para llegar a un acuerdo, primero reflexiona sobre lo siguiente.
- ¿Qué forma tienen los tubos construidos con las láminas de cartulina?
- ¿A qué concepto matemático hace referencia el espacio que ocupa un cuerpo?
Observa que cada cuerpo que construyeron, tiene una superficie curva delimitada por la hoja. Si se colocaran tapas al tubo, serían dos círculos iguales y paralelos entre sí, que conformarían las bases del cuerpo. Si se mide la distancia perpendicular entre esas bases, se obtendría la medida de la altura. A los cuerpos con estas características se les llama cilindros rectos.
El espacio que ocupa un cuerpo, hace referencia al concepto de volumen.
Con base en estas reflexiones se puede proponer que, para resolver el problema de los tubos, una opción consiste en considerar a los tubos como cilindros rectos, calcular el valor del volumen de cada uno y comparar esos valores.
Ahora bien, si se requiere calcular el valor del volumen de cilindros rectos, cabe preguntarse ¿de qué depende el valor del volumen de un cilindro recto?
El equipo 1, únicamente tomó en cuenta el tamaño de los rectángulos con que se construyeron los tubos. Entonces este equipo únicamente consideró la medida de la superficie curva del cilindro. ¿Piensas que el valor del volumen del cilindro recto depende únicamente de la medida de su superficie curva?
El equipo 2, tomó en cuenta únicamente la medida de la altura de los cilindros. ¿El valor del volumen del cilindro recto dependerá únicamente de esa medida?
El equipo 3, únicamente consideró la medida del área de una de las bases de cada cilindro y la medida de su altura. ¿El valor del volumen del cilindro recto dependerá únicamente de esas medidas?
Para averiguar de qué medidas depende el valor del volumen de un cilindro recto, puedes considerar lo que sabes sobre el volumen de prismas rectos con base un polígono regular y reflexionar sobre si existe alguna relación entre el volumen de esos prismas y el volumen de los cilindros.
El valor del volumen de un prisma triangular recto, se calcula multiplicando la medida del área de su base por la medida de su altura.
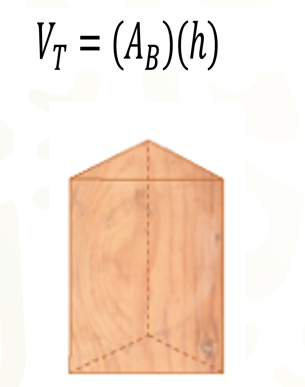
¿Cómo puedes calcular el valor del volumen de cualquier prisma recto con base un polígono regular, tomando en cuenta el valor del volumen de un prisma triangular recto?
Considera un prisma recto con base un polígono regular e imagina que lo divides en prismas triangulares rectos iguales, como se muestra en la imagen. Entonces el volumen del prisma recto será la suma de los volúmenes de un número de prismas triangulares rectos.
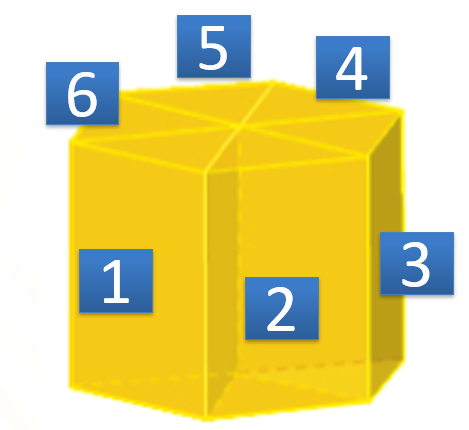
En el caso del prisma que tiene de base un hexágono regular, está dividido en seis prismas triangulares iguales.
El valor del volumen de este prisma recto en particular puede calcularse como valor del volumen del prisma recto con base un hexágono regular, es igual al valor del volumen del prisma triangular recto número 1, más el valor del volumen del prisma triangular recto número 2, más el valor del volumen del prisma triangular recto número 3, más el valor del volumen del prisma triangular recto número 4, más el valor del volumen del prisma triangular recto número 5, más el valor del volumen del prisma triangular recto número 6.
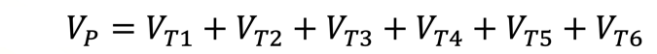
Luego, si el valor del volumen de cada prisma triangular se expresa en términos del área de su base y del valor de su altura, se obtiene.
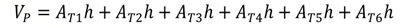
Ahora, considera que es lo mismo multiplicar primero “a” por “b”, “a” por “c”, “a” por “d”, “a” por “e”, y luego sumar los productos, que sumar primero números “b”, “c”, “d”, “e” y luego multiplicar el resultado por un número “a”.
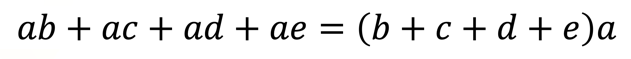
Observen que en la fórmula obtenida para calcular el valor del volumen del prisma con base un hexágono regular primero se multiplica el valor del área de cada base de los prismas triangulares por el valor su altura y luego se suman todos los resultados. Esto es equivalente a sumar primero el valor del área de todas las bases de los prismas triangulares y luego multiplicar esta suma por el valor de su altura.
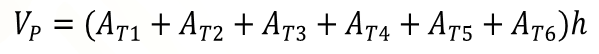
Así se llega a que el valor del volumen del prisma recto con base un hexágono regular es igual a realizar la suma del valor del área de la base del prisma triangular número 1, más el valor del área de la base del prisma triangular número 2, más el valor del área de la base del prisma triangular número 3, más el valor del área de la base del prisma triangular número 4, más el valor del área de la base número 5, más el valor del área de la base número 6 y luego multiplicar el resultado por el valor de la altura de uno de los prismas triangulares rectos.
La suma del valor del área de las seis bases de los prismas triangulares rectos, es igual al valor del área de la base del prisma recto con base un hexágono regular. El valor del volumen del prisma recto con base un hexágono regular, es igual al valor del área de su base por el valor de su altura.
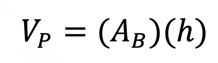
Este procedimiento es válido para cualquier prisma recto con base un polígono regular, siempre y cuando se pueda dividir al prisma recto con base un polígono regular en prismas triangulares iguales.
Ahora bien, ¿puedes encontrar alguna relación entre el volumen de un prisma recto con base un polígono regular y el volumen de un cilindro recto?
Imagina que inscribes un prisma recto con base un polígono regular en un cilindro recto, como se muestra en la siguiente imagen. ¿Qué observas? Considera todos los elementos que componen este nuevo arreglo.
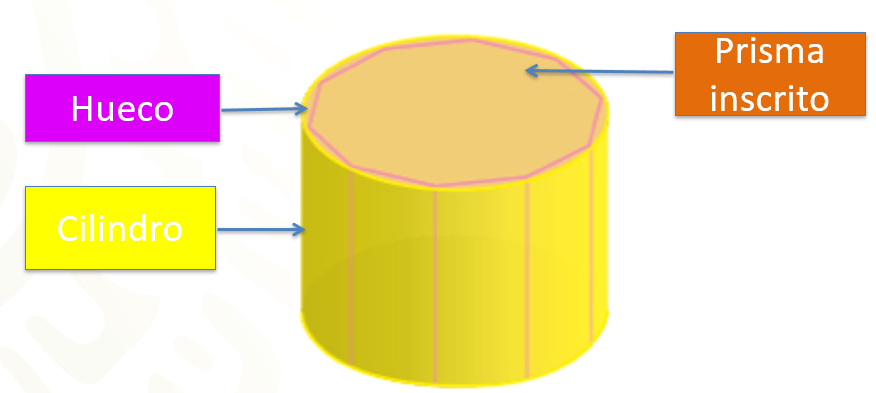
Se puede observar el prisma recto, el cilindro, pero también un hueco entre el prisma recto y el cilindro. Además, en la base del arreglo se puede observar una diferencia entre el área de la base del prisma recto y el área de la base del cilindro. A partir de estos elementos, ¿cómo puedes relacionar el valor del volumen del prisma recto con base un polígono regular y el valor del volumen del cilindro recto?
Sabes que para obtener el valor del volumen del prisma recto se utiliza la fórmula “V” es igual a “A” subíndice “B” por “h”, en donde “V” representa el valor del volumen del prisma, “A” subíndice “B” representa el valor del área de la base del prisma y “h” representa la medida de su altura.
¿De qué otra manera se puede expresar esa fórmula, pero ahora tomando en cuenta el valor del volumen del hueco entre el prisma recto y el cilindro, así como el valor de la diferencia entre el valor del área de la base del prisma recto y el valor del área de la base del cilindro?
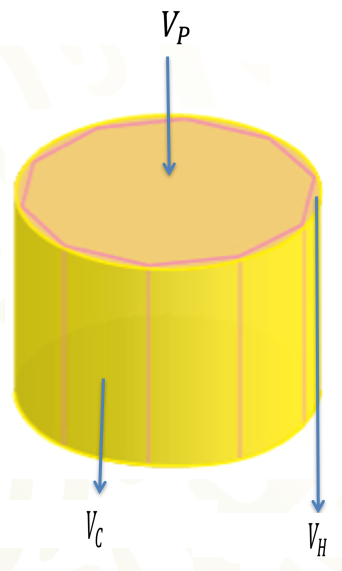
Considera el primer miembro de la fórmula “V” igual a “A” subíndice “B” por “h”, en donde “V” representa el valor del volumen del prisma recto. ¿Qué puedes hacer con el valor del volumen del cilindro recto para obtener el valor del volumen del prisma recto?
Si al valor del volumen del cilindro le restas el valor del volumen del hueco entre el prisma recto y el cilindro, se obtiene el valor del volumen del prisma. Entonces la letra “V” de la fórmula “V” igual a “A” subíndice “B” por “h”, que representa el valor del volumen del prisma se puede escribir como el valor del volumen del cilindro menos el valor del volumen del hueco entre el prisma recto y el cilindro.
El valor de la altura del cilindro es la misma que el valor de la altura del prisma recto, sin embargo, el valor del área de las bases es distinta. ¿Qué puedes hacer con el valor del área de la superficie del círculo que conforma la base del cilindro para obtener el valor del área de la superficie del prisma que conforma la base del prisma?
Observa que, si al valor del área de la base circular del cilindro se le resta el valor de la diferencia entre el valor del área de la base del prisma recto y el valor del área de la base del cilindro, se obtiene el valor del área de la base del prisma recto. Entonces, si se asigna “C” al valor del área de la base circular del cilindro y “Y” a la diferencia entre el valor del área de la base del prisma recto y el valor del área de la base del cilindro, la expresión “A” subíndice “B” de la fórmula “V” igual a igual a “A” subíndice “B” por “h”, que representa el valor del área de la base del prisma recto, se puede escribir como “C” menos “Y”.
De acuerdo con lo anterior, una expresión que relaciona el volumen del cilindro recto y el prisma recto inscrito, se puede escribir como valor del volumen del cilindro menos el valor del volumen del hueco entre el prisma recto y el cilindro, es igual la diferencia entre “C” y “Y”, por “h”, en donde “C” es el valor del área de la superficie circular del cilindro, “Y” la diferencia entre el valor del área de la base del prisma recto y el valor del área de la base del cilindro y “h” el valor de la altura del prisma (que es igual que la del cilindro).
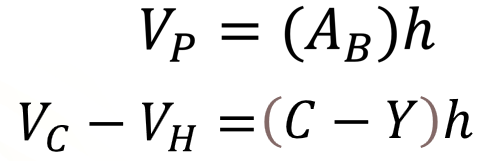
Ahora bien, en esta nueva expresión, el valor del volumen del hueco entre el prisma recto y el cilindro y la diferencia entre el valor del área de la base del prisma recto y el valor del área de la base del cilindro, pueden variar porque dependen del número de caras del prisma recto que se encuentre inscrito del cilindro. Pero en todos los casos, el valor del volumen del cilindro siempre permanecerá constante.
Si se supone que se puede construir un prisma recto tal que el valor del volumen del hueco entre el prisma recto y el cilindro y la diferencia entre el valor del área de la base del prisma recto y el valor del área de la base del cilindro son cero, entonces la expresión resultante que se obtiene es valor del volumen del cilindro igual a “C”, que es el valor del área de la base circular de una de las bases del cilindro, por “h”, que es el valor de la altura del prisma.
Como el área de un círculo es “pi” por el valor del radio al cuadrado, el valor del volumen del cilindro puede expresarse como volumen del cilindro igual a “pi” por el valor del radio de una de las bases al cuadrado, por el valor de la altura.
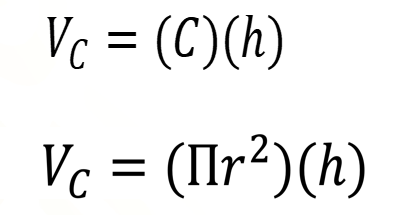
Con base en la expresión obtenida, se puede concluir que el valor del volumen del cilindro recto depende del valor del área de su base y del valor de su altura, como en cualquier prisma recto. Si se retoman las respuestas de los estudiantes, parece que el equipo 3 está en lo correcto, porque calculó el área de una de las bases del cilindro y midió su altura. Con base en cálculos con esas mediciones, el equipo afirmó que el cilindro más bajo ocupa el mayor volumen. A continuación, realizarás los cálculos para averiguar si esa afirmación es correcta.
De acuerdo con el problema, las láminas con las que fueron construidos los tubos son del mismo tamaño y miden 35.6 centímetros de largo por 20 centímetros de ancho.
Considera cómo fueron construidos los tubos y reflexiona sobre, ¿qué parte de la lámina rectangular corresponde a la circunferencia del cilindro?, ¿qué parte de la lámina rectangular corresponde a la altura del cilindro?
Puedes utilizar los cilindros que construiste para reflexionar sobre las respuestas a las preguntas anteriores.
Considera primero, el cilindro que se construyó uniendo los lados más largos del rectángulo. Puedes percatarte de que el lado más largo de la hoja corresponde a la altura del cilindro. Luego dirige la mirada en una de las bases del cilindro. Al despegar los lados que se unieron, observa que la longitud de la circunferencia de la base corresponde a la longitud del ancho de la hoja.
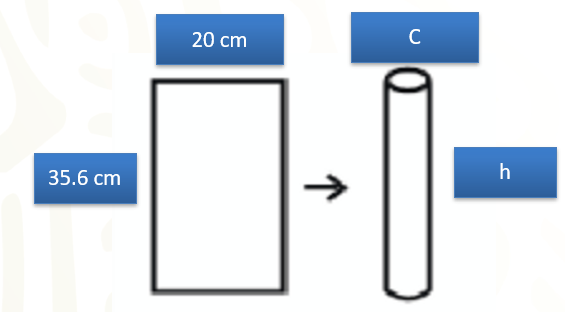
Con base en lo anterior, puedes notar que la longitud de la circunferencia mide 20 centímetros y la altura mide 35.6 centímetros.
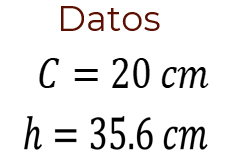
Se tiene entonces la medida de la circunferencia y la medida de la altura. Pero la fórmula del volumen del cilindro que se obtuvo anteriormente involucra el valor del radio de la base del cilindro recto. ¿Cómo se puede obtener la medida de ese radio a partir de conocer la medida de la circunferencia?
Una fórmula que relaciona la medida de una circunferencia con la medida de su radio es.
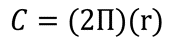
De aquí se obtiene que.
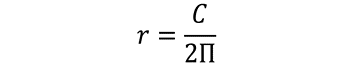
Al sustituir los valores se obtiene.
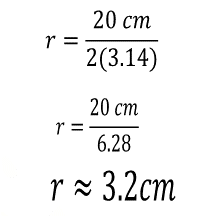
Con esto, ya se conoce el valor aproximado del radio de la circunferencia de la base del cilindro, que es de 3.2 centímetros. También se sabe que el valor de la altura del cilindro es 35.6 centímetros.
Al sustituir estos valores en la fórmula, valor del volumen del cilindro igual al valor del área de la base por el valor de la altura, se obtiene que.

De acuerdo con esto, el valor del volumen del cilindro más alto, es de aproximadamente 1,144.54 centímetros cúbicos.
Considera ahora el cilindro que se construyó uniendo los lados más cortos del rectángulo. Para este cilindro, la longitud de la circunferencia mide 35.6 centímetros y la altura mide 20 centímetros.
Para calcular el valor del radio de la base se puede considerar que es igual al valor de la longitud de la circunferencia entre dos “pi”, como en el caso del cilindro anterior. Al sustituir los valores, se obtiene.

Con esto ya se conoce el valor aproximado del radio de la circunferencia de la base del cilindro que es de 5.7 cm. También se sabe que el valor de la altura del cilindro es 20 centímetros.
Al sustituir estos valores en la fórmula valor del volumen del cilindro igual al valor del área de la base por el valor de la altura, se obtiene que.

Por tanto, el valor del volumen del cilindro más bajo es de 2,040 centímetros cúbicos aproximadamente.
Comparando el valor de este volumen con el del volumen del cilindro más alto, que fue de 1,144.54 centímetros cúbicos, se concluye que efectivamente el cilindro más bajo es el del mayor volumen y, por tanto, el que ocupa mayor espacio.
Con esto, se responde el problema inicial y se concluye la sesión. En esta sesión, se obtuvo que el valor del volumen de un cilindro recto es igual al valor de “pi” por el valor del radio de la base al cuadrado por el valor de la altura. También se utilizó esta fórmula para calcular el volumen de cilindros.
¡Buen trabajo!
Gracias por tu esfuerzo.
*Este material es elaborado por la Secretaría de Educación Pública y actualizado por la Subsecretaría de Educación Básica, a través de la Estrategia Aprende en Casa*.
Para saber más:
Lecturas