Uso de regla y compás para trazar las alturas en un triángulo
Uso de regla y compás para trazar las alturas en un triángulo
Aprendizaje esperado: explora características y propiedades de las figuras y cuerpos geométricos.
Énfasis: usar regla y compás para trazar las alturas de triángulos.
¿Qué vamos a aprender?
¿Sabías que, desde Pitágoras, nacido en Samos, Grecia, en el año 579 antes de nuestra era, la matemática en la Antigüedad era sinónimo de geometría? ¿Y que las actuales herramientas de la regla y el compás son un símil de la cuerda que se ocupaba entonces?
¿Qué hacemos?
Para Platón, que era de Atenas, Grecia, nacido en el 427 antes de nuestra era, seguidor de las ideas del maestro Pitágoras, lo más importante era pensar las cosas y deducir la verdad de éstas a partir de la observación.
Platón consideró fundamental que aquellos que desean acceder al conocimiento, debían de hacerlo a partir del estudio de la geometría, norma que se subrayó con la frase expuesta en el dintel de la Academia:

De igual manera, a Platón se le debe la restricción del uso de la regla y el compás como instrumentos únicos para el trazo de objetos geométricos construibles, ya que él creía que eran los únicos objetos capaces de respetar la configuración de la simetría.
Pero ¿por qué la regla y el compás? porque son los instrumentos que precisan y facilitan la construcción de las curvas, las rectas y las circunferencias.
Asimismo, todas las construcciones con regla y compás debían ser aplicaciones sucesivas de cinco construcciones básicas, usando en cada una de ellas puntos, rectas y círculos.
Estas cinco construcciones posibles son:
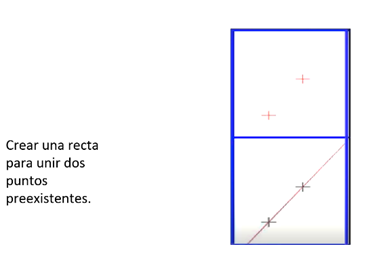
- Crear una recta que une dos puntos preexistentes, aunque en el mundo real sólo es posible construir un segmento de recta.
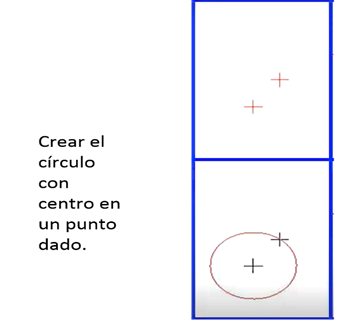
- Crear el círculo con centro en un punto dado, y cuyos puntos, cualesquiera de ellos, tocan otro punto dado.
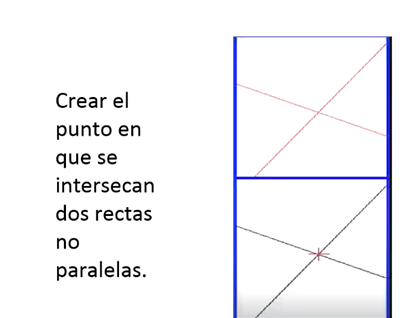
- Crear el punto en el que se intersecan dos rectas no paralelas.
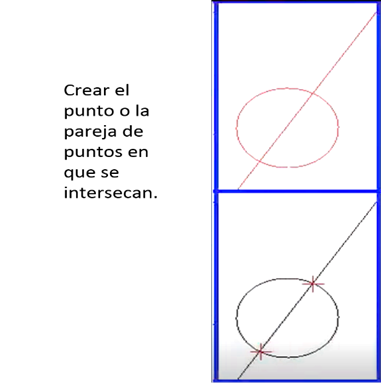
- Crear el punto o la pareja de puntos en los que se intersecan, si lo hacen, una línea y un círculo.
Y crear el punto o la pareja de puntos en los que se intersecan, si lo hacen, dos círculos.
Como se ha demostrado, las construcciones en la Antigüedad se realizaban empleando las cinco construcciones posibles permitidas. Lo anterior es mediante la intersección de rectas y circunferencias, usando exclusivamente la regla no graduada y el compás, los instrumentos divinos, considerados así por Platón.
Para él, todos los instrumentos de medida eran imperfectos, con excepción de la regla y el compás.
Sin embargo, las construcciones con regla y compás llevaron a los griegos a tres problemas que no pudieron resolver.
- Dado un cubo de cierto tamaño, ¿es posible construir otro cubo con el doble del volumen?
- ¿Es posible trisecar un ángulo?
- ¿Es posible cuadrar el círculo?
La “duplicación del cubo” consiste en construir con regla y compás la arista de un cubo cuyo volumen sea el doble del volumen de un cubo dado.
La “trisección del ángulo” consiste en construir con regla y compás las semirrectas que dividen un ángulo en tres ángulos iguales.
Y la “cuadratura del círculo” consiste en construir con regla y compás un cuadrado con la misma área que un círculo dado.
A partir de estos reconocidos problemas, al no hallarles solución, muchos matemáticos, siglos más tarde, se dedicaron a su estudio.
El compás antiguo o euclidiano estaba construido de manera que, cuando se levantaba de la superficie, sus brazos se cerraban automáticamente, lo que imposibilitaba trasladar las medidas. Pero este compás era útil en tanto que ambos brazos hicieran contacto con el papel.

Como se hace notar, el compás antiguo y el moderno son semejantes —aunque con el primero se pueden hacer construcciones menos precisas—, ya que las patas podían cerrarse o abrirse inadvertidamente. Mientras que, con el segundo compás, se puede estar seguro de que la abertura requerida es la que se necesita.
Es importante mencionar que el compás es un instrumento de medición, pues, a partir de éste, se pueden reproducir distancias con precisión en las construcciones geométricas.
Es así como, durante la sesión, ustedes utilizarás el compás moderno para los trazos de triángulos y sus alturas.
Con esto último, se puede observar la influencia que tuvieron tanto Pitágoras como Platón en el desarrollo de la geometría, misma que aún se reconoce en las distintas ramas de la matemática.
Puedes notar lo indispensable que es el legado de Pitágoras y Platón en el pensamiento actual y la geometría.
Es así como, para comenzar la práctica, se reitera emplear únicamente la regla, el compás y el transportador para trazar un triángulo, y que después se les clasifique según los criterios existentes.
Para tal efecto, observa el siguiente audiovisual, si te es posible, replícalo al trazar su propio triángulo.
Para aprender a trazar triángulos con regla y compás:
- Video 1
https://youtu.be/eZiYMJkaDw8?t=420
Del minuto 7:00 a 11:42
Primero se identifican las medidas del triángulo a trazar: 7 cm, 6 cm y 5 cm.
Y se traza el primer segmento de recta, llamado AB, con la medida de 7 cm, utilizando la regla.
A continuación, se abre el compás a 6 cm, que es la medida del segmento de recta CA.
Al tener 6 cm en el compás, se hace el centro en el primer extremo del segmento de recta y se traza un arco.
Después se abre el compás 5 cm, se asigna el centro en el otro extremo del segmento de recta y se traza otro arco que corte al primero.
El punto de corte de los dos arcos es el tercer vértice del triángulo que se forma; desde este mismo punto, se realiza la unión de los otros dos vértices.
Con esto, se ha trazado el triángulo, pero falta clasificarlo según la medida de sus lados y sus ángulos. Por la medida de sus lados, se sabe que un lado mide 7 cm; otro, 6 cm, y otro más de 5 cm.
Por lo tanto, de acuerdo con la medida de sus lados, el triángulo es escaleno.
Para clasificarlo por sus ángulos, se utiliza el transportador: se alinea la marca central del transportador con el cero y se observa que mide 45°.
Y de nueva cuenta se realiza lo mismo con el otro ángulo: se alinea a la marca central del transportador con el cero para reconocer que este ángulo mide 55°.
De este modo, sólo queda por realizar la medida del tercer ángulo. Para ello se emplean los conocimientos previos, sabiendo que la suma de los ángulos internos de un triángulo es de 180°; si se suman 45° más 55°, se obtiene 100°, mismos que al restarse a 180°, dan como resultado 80°.
Para comprobar que efectivamente el último ángulo mide 80°, se toma el transportador, se alinea con el cero y se verifica su medida. Así, se tiene que este triángulo se clasifica por sus lados en un triángulo escaleno, y que, por sus ángulos, en un triángulo acutángulo.
Otro de los matemáticos que contribuyó en el desarrollo y la solución de triángulos rectángulos fue Euclides.
Euclides, que vivió entre el tercer y segundo siglo antes de nuestra era, fue un matemático griego reconocido en la actualidad por sus escritos, una serie de libros en donde sintetiza los conocimientos matemáticos conocidos hasta entonces.
En su teorema, Euclides propone que, en todo triángulo rectángulo, cuando se traza la altura que corresponde al vértice del ángulo recto con respecto a la hipotenusa, se forman dos triángulos rectángulos.
Para este caso, se toma un fragmento del teorema de Euclides para comprender las alturas de un triángulo y así trazarlas.
Las alturas son las rectas que pasan por uno de sus vértices, y perpendiculares al lado opuesto de dicho vértice, o a su prolongación.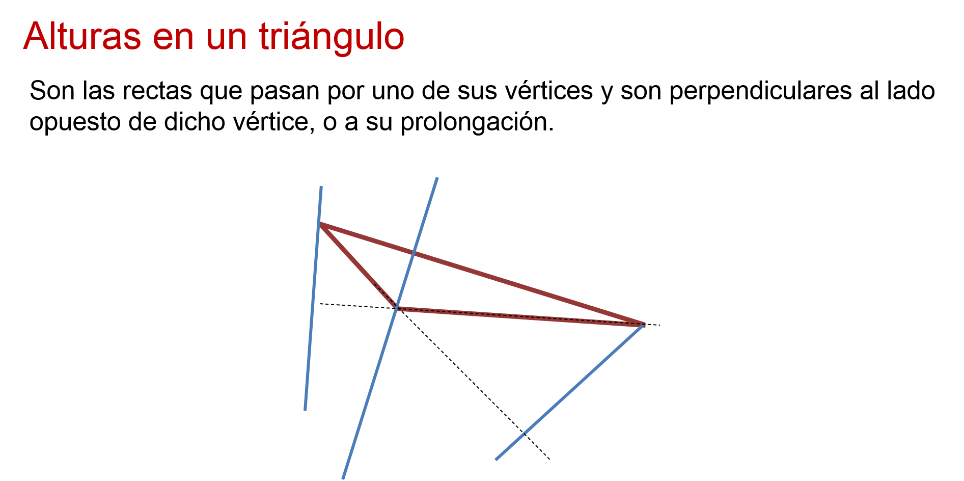
Un triángulo tiene tres alturas:
Para demostrarlo, traza las alturas en un triángulo acutángulo, por lo que requieres tu cuaderno u hojas, lápiz o lápices de colores, y la escuadra o regla.
Primero se tiene el triángulo acutángulo con vértices ABC.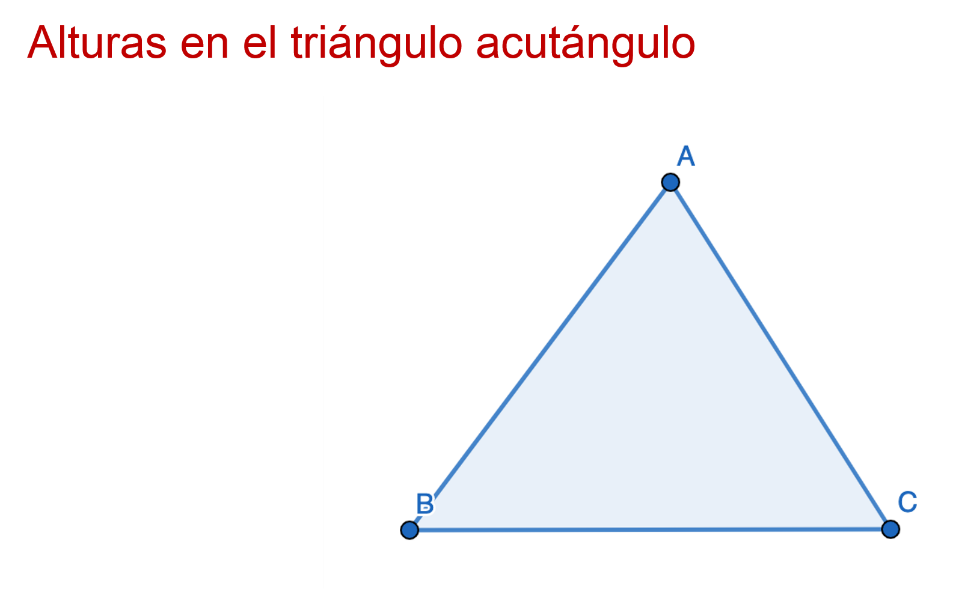
Se considera como vértice A, asegurándose que la escuadra esté apoyada en su totalidad en el lado opuesto, y que pase por el vértice. Después se traza la línea perpendicular y, para ello, se emplea la regla u otra escuadra.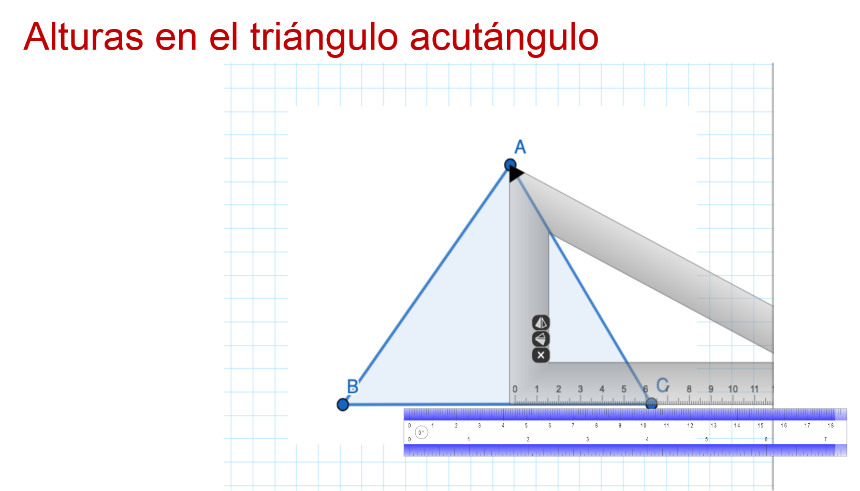
Con esto, se tiene la altura que va del vértice A con el lado opuesto. No se tiene por objeto dividir el triángulo, sino formar ángulos rectos.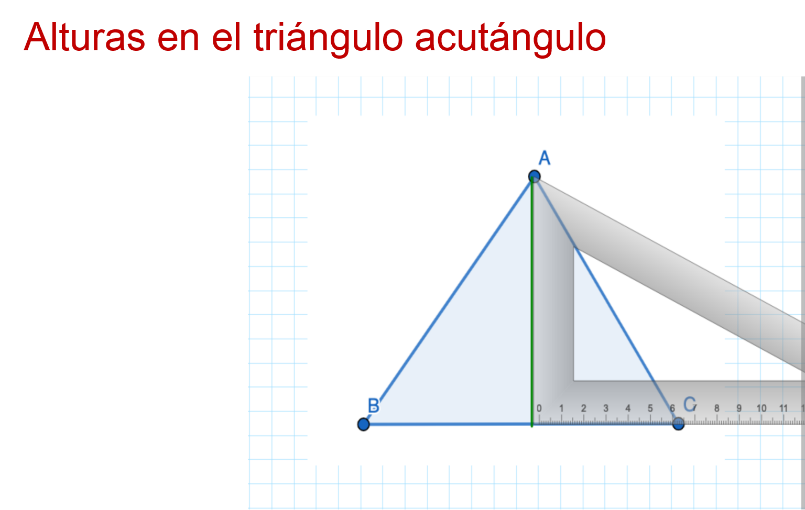
Y se repite el procedimiento para el lado B: se apoya la escuadra en el lado opuesto al vértice B y se dibuja el segmento de recta del vértice B al lado opuesto con una línea perpendicular, asegurándose de que se forme un ángulo recto de 90 grados.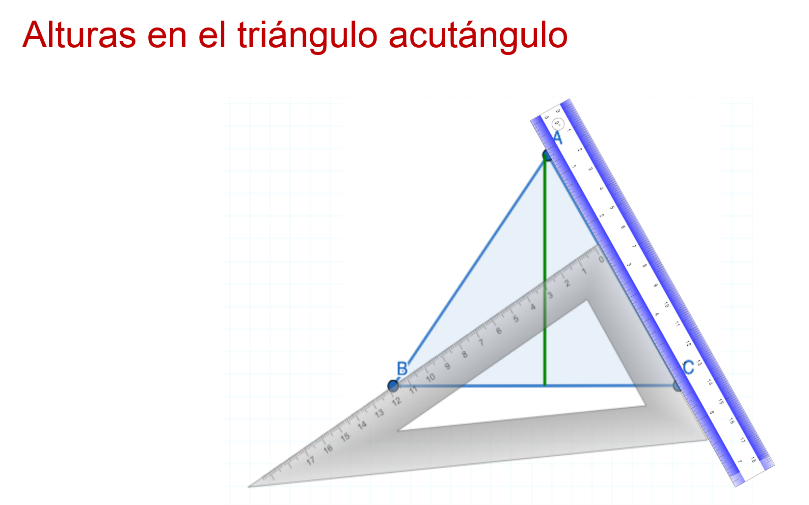
De esta manera, se obtiene una segunda altura.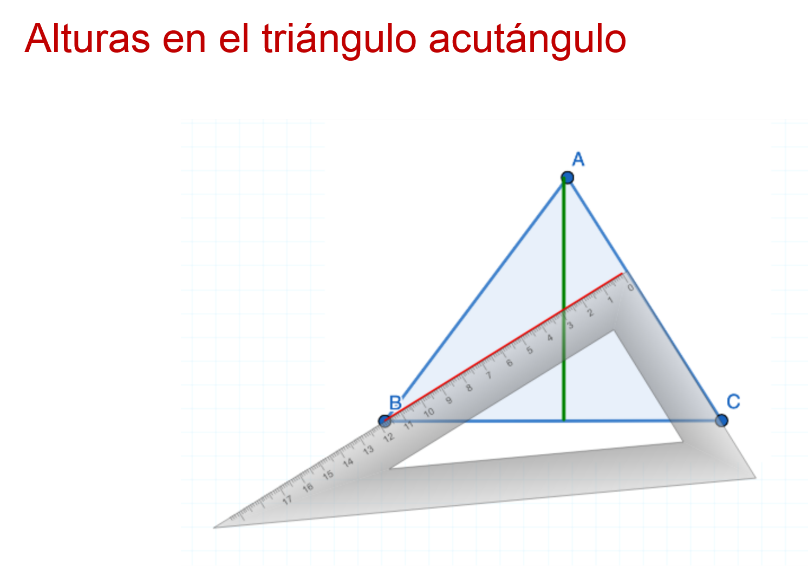
Y se repite el procedimiento para el lado que falta, en este caso, el C.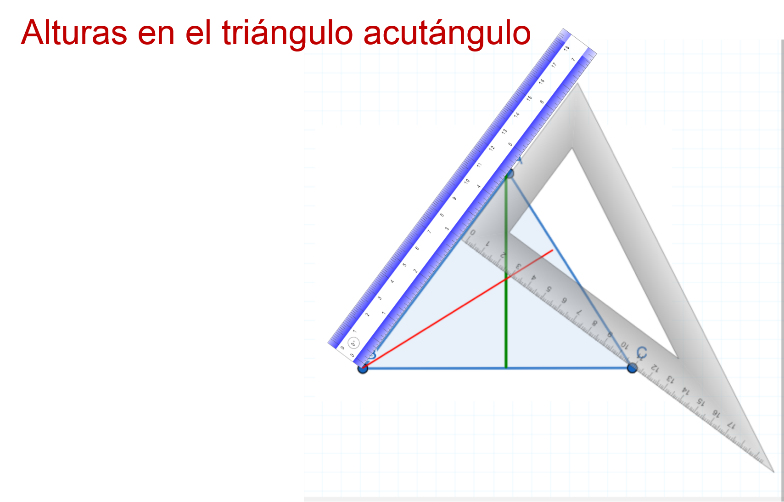
Apoyando la escuadra en el lado C, y que coincida con el vértice C, se traza la línea perpendicular.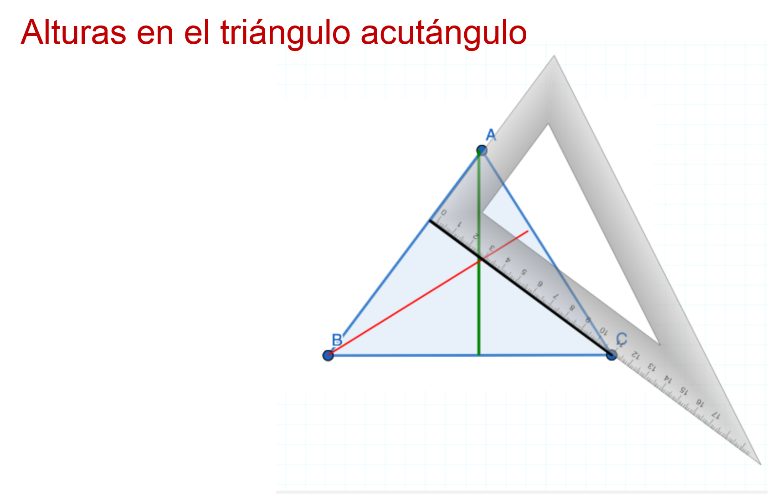
Es así como las tres alturas de un triángulo se cortan en un mismo punto llamado ortocentro, identificado en color amarillo.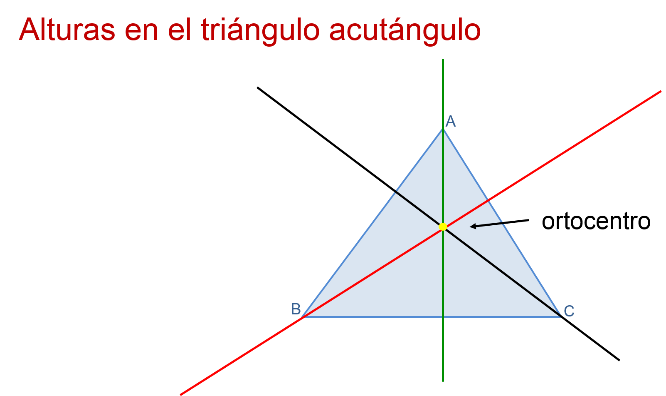
¿Reconociste cómo las alturas se intersecan en un punto? Este punto es el antes mencionado, ortocentro.
Se sigue con un nuevo ejemplo al trazar las alturas en un triángulo obtusángulo.
En color verde se tiene un triángulo obtusángulo con vértices ABC.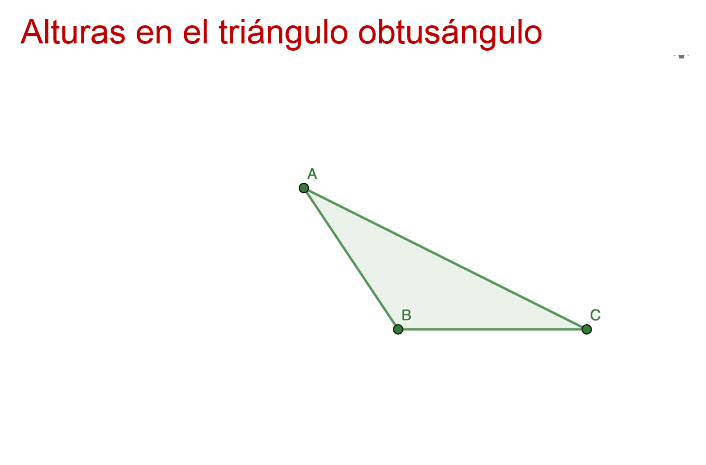
Primero se dibuja una línea perpendicular al vértice A y hasta la prolongación del lado opuesto.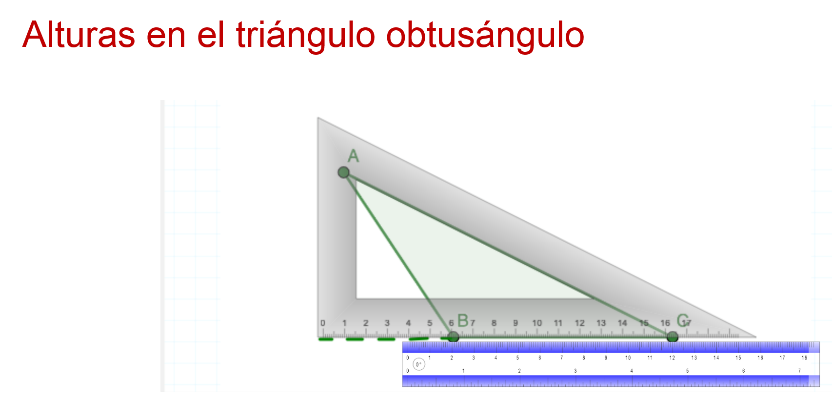
Sobre esta prolongación se apoya la escuadra y se traza la altura, que también se prolonga.
Y se dibuja la segunda altura, coincidiendo el vértice B con el lado opuesto.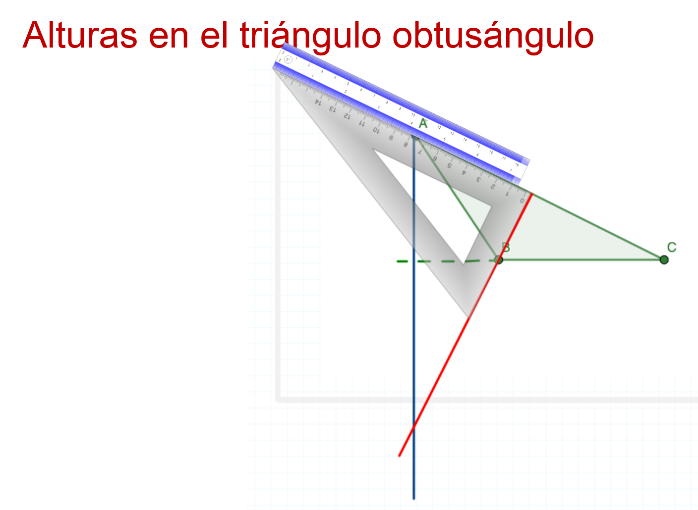
Mientras que, para la tercera altura, se prolonga de nueva cuenta el segmento de recta del lado opuesto al vértice C.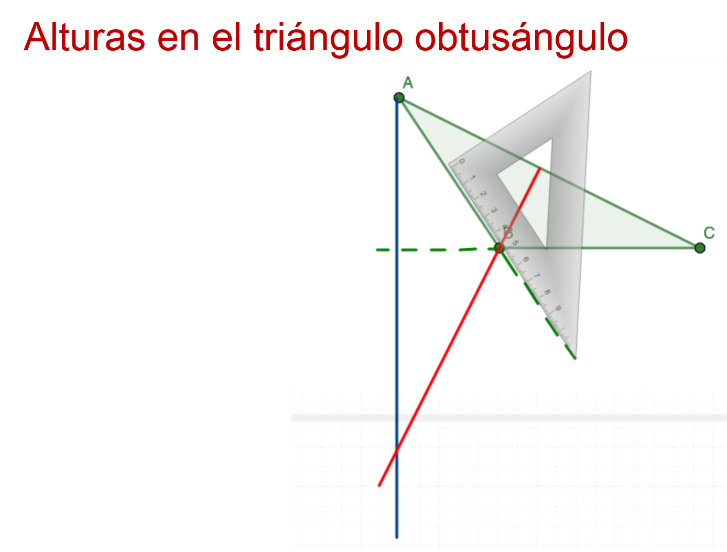
Y se apoya la escuadra en esa misma prolongación hasta coincidir el vértice C con la prolongación, y trazar la altura.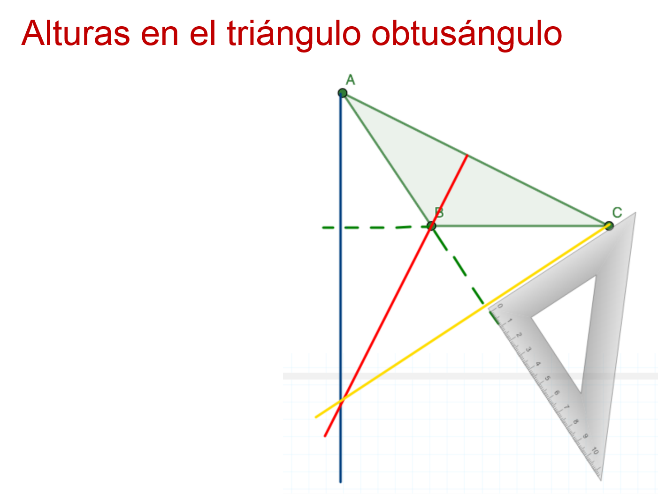
Finalmente, se verifica que las tres alturas coincidan en el ortocentro que se localiza fuera del triángulo.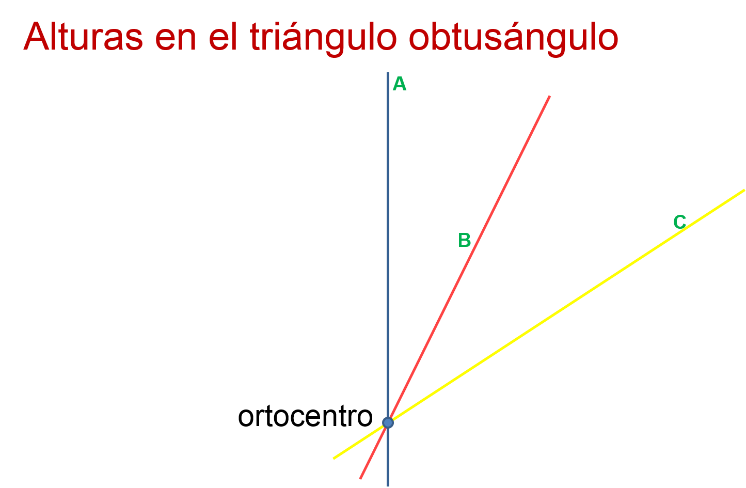
¿Reconociste cómo las alturas se intersecan en un punto? Ya sabes que este punto es el ortocentro.
Asimismo, notaste que las ubicaciones del ortocentro del triángulo acutángulo y obtusángulo son distintas.
Para ello, observa el siguiente audiovisual, en el que el triángulo acutángulo y el ortocentro se encuentra dentro del triángulo; en el triángulo rectángulo se encuentra en el ángulo recto, y en el triángulo obtusángulo está en el exterior del triángulo. - Video 2
Del minuto 16:10 a 19:32
Utilizando un programa de geometría, se trazan las alturas de tres distintos triángulos, y observa cómo el ortocentro cambia de posición de acuerdo con el tipo de triángulo trazado. En algunos triángulos se encuentra al centro, mientras que, en otros, en un vértice o en el exterior.
Se traza un triángulo, verificando la medida de sus ángulos para obtener un triángulo acutángulo.
Ya se sabe que las alturas de un triángulo son las rectas que pasan por uno de sus vértices, y que son perpendiculares al lado opuesto del mismo o a su prolongación.
Se traza la altura del vértice A utilizando el lado opuesto, la del vértice B y la del C; observa cómo las alturas se intersecan en el punto llamado ortocentro. De este modo, se interactúa con la forma de este triángulo acutángulo para observar cómo se mueve el ortocentro sin salir del triángulo trazado.
Después se mueve el vértice A para formar un triángulo rectángulo. Es así como se reconoce que el ortocentro se encuentra en el vértice donde se forma el ángulo recto o de 90 grados, y se interactúa con la forma del triángulo, desplazando el vértice A hacia la derecha hasta formar nuevamente un triángulo rectángulo invertido. Y, finalmente, se verifica nuevamente que el ortocentro está donde se forma el ángulo recto.
Pero se mueve una vez más uno de los vértices hasta formar un triángulo obtusángulo para observar cómo el ortocentro sale del triángulo. Esto se debe a que la altura se traza utilizando uno de sus lados proyectado. Si se mueve uno de los vértices hacia la izquierda hasta formar nuevamente un triángulo obtusángulo, el ortocentro sale del triángulo.
Tomando en cuenta que un triángulo tiene tres alturas, la que se necesita es la formada con el vértice donde se encuentra el ángulo recto y que corta perpendicularmente el lado opuesto al ángulo recto.
Retomando el teorema de Euclides: se tiene que, en todo triángulo rectángulo:
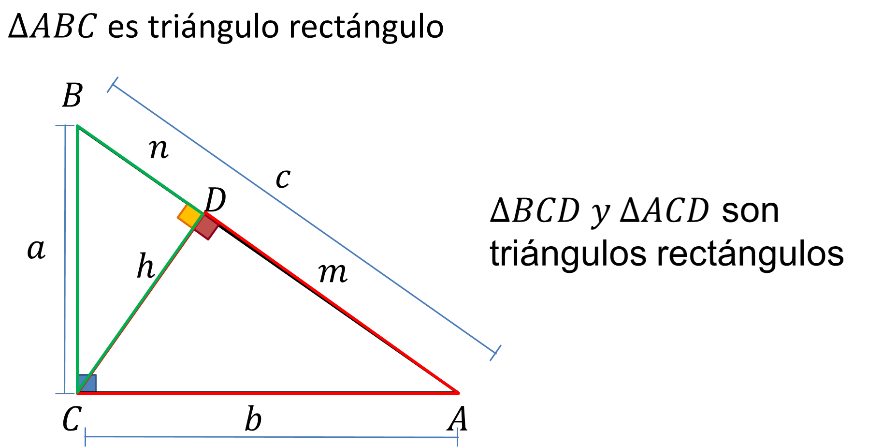
Cuando se traza la altura que corresponde al vértice del ángulo recto con respecto a la hipotenusa, se forman dos triángulos rectángulos.
Ya sabes que este teorema te permite inferir que:
Los ángulos de los tres triángulos son iguales, y que son semejantes entre sí, lo que significa sus lados semejantes son proporcionales entre sí.
Con esto, se da por sentado que, desde la semejanza de triángulos, se establecen dos teoremas: el teorema de la altura y el teorema de los catetos.
El teorema de la altura relaciona la altura de un triángulo rectángulo con las proyecciones de los catetos sobre la hipotenusa, por lo que permite calcular la altura de un triángulo rectángulo cuando se tienen estas proyecciones.
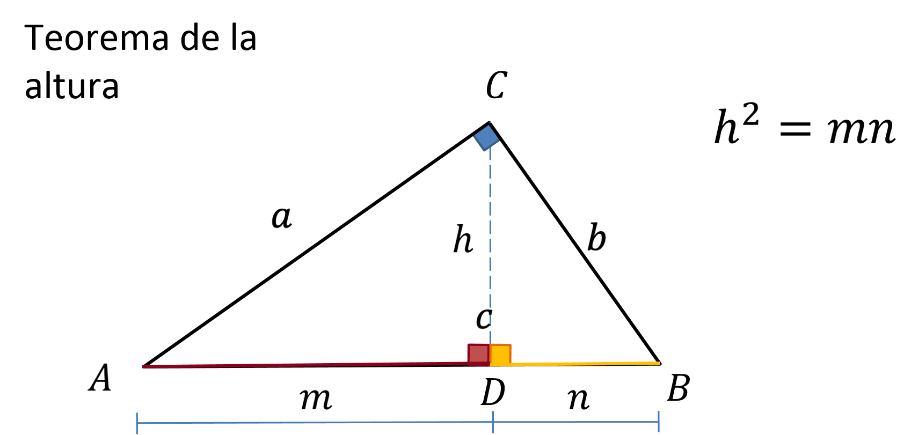
La fórmula del teorema de la altura es “h” al cuadrado, igual a “m” por “n”.
Para emplear el teorema de la altura, primero se debe comprender qué son las proyecciones de los catetos sobre la hipotenusa.
Se comienza del siguiente triángulo rectángulo, colocado de forma que la hipotenusa queda en la parte de abajo:
En donde:
El lado a es el cateto mayor.
El lado b es el cateto menor.
Y el lado c es la hipotenusa.
Es decir, si se instala un foco de luz encima del triángulo, la sombra que proyecta el lado “a” sobre la hipotenusa corresponde a la proyección del cateto mayor en la hipotenusa y que, a su vez, corresponde al segmento en color rojo o “m”.
De la misma manera, la sombra que proyecta el lado “b” sobre la hipotenusa corresponde a la proyección del cateto menor en la hipotenusa, y que corresponde al segmento en color amarillo o “n”.
Es importante destacar que ambas proyecciones están separadas por una línea vertical, que corresponde a la altura del triángulo rectángulo, y que la altura separa, a su vez, el triángulo en otros dos triángulos rectángulos.
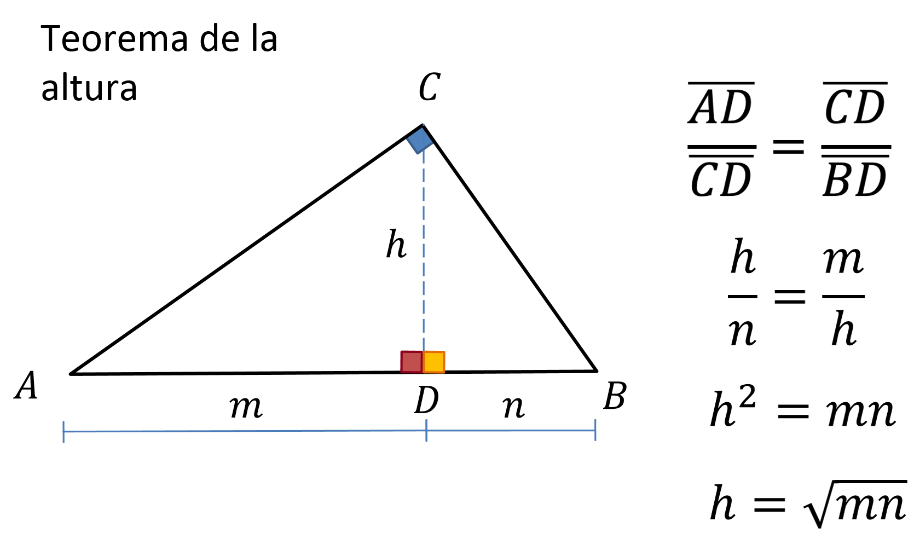
En ambos triángulos que son semejantes se compara su relación entre el cateto menor y el cateto mayor.
Obteniendo así “h” entre “n” es igual a “m” entre “h”.
De donde se despeja “h”, que corresponde a la altura del triángulo rectángulo original.
Para ello, se multiplican en cruz ambas fracciones, pasando cada denominador, multiplicando al miembro contrario.
Así, se opera en ambos miembros; queda “h” cuadrada en uno de ellos.
Y se despeja la altura para obtener la fórmula que relaciona la altura con las proyecciones de los catetos en la hipotenusa: “h” es igual a raíz cuadrada de “m por n”.
Este teorema tiene distintas aplicaciones desde la Antigüedad, por ejemplo, calcular alturas o distancias. Actualmente, su aplicación es empleada para la ingeniería y la física, por mencionar algunas.
Con estos nuevos conocimientos, se puede calcular una distancia sin recorrerla. Asimismo, se puede calcular un recorrido o elegir la distancia más corta. Además, se pueden calcular distancias de difícil acceso, como lo hacen los topógrafos e ingenieros.
De este modo, ya se puede aplicar lo aprendido en una situación-problema y encontrar su solución.
Las casas de Ana, de su amiga, de su abuelita y la escuela secundaria se encuentran ubicadas como se muestra en la imagen.
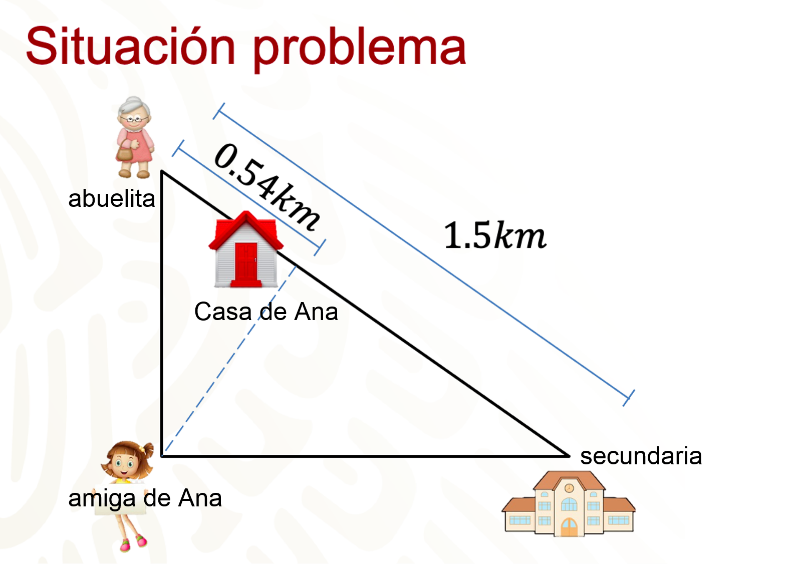
La distancia de la casa de la abuelita a la secundaria es de 1.5 km, y entre la casa de la abuelita y la casa de Ana es 0.54 km.
Además, su amiga afirma que la distancia de su casa a la casa de Ana es mayor que la de casa de Ana a la de la abuelita, pero menor que la distancia de la casa de Ana a la secundaria.
De este modo, se debe identificar que la figura es un triángulo rectángulo, y que la distancia entre la casa de Ana a la de su amiga corresponde a la altura que está trazada en el triángulo rectángulo mayor del esquema. Con estos datos, se puede aplicar el teorema de la altura.
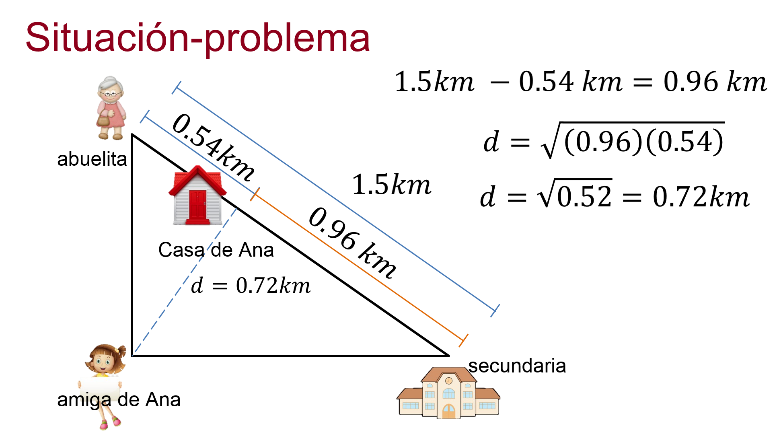
Se sabe que de la casa de Ana a la de su abuelita son 0.54 km y de la casa de su abuelita a la secundaria son 1.5 km.
Eso hace que, de la casa de Ana a la secundaria, sean 0.96 km.
Y aplicando el teorema de la altura:
Se tiene que la distancia de la casa de Ana a la casa de su amiga es la raíz cuadrada de multiplicar las distancias de su casa a la secundaria, y de su casa a la de su abuelita, lo cual da 0.72 km.
Así, la amiga de Ana tiene razón en su afirmación, debido a que 0.72 km es mayor que 0.54 km y menor a 0.96 km.
Repasa lo aprendido.
Pitágoras, Platón y Euclides han tenido una gran influencia en la geometría y en las distintas ramas de la matemática.
En la Antigüedad se utilizaba un compás euclidiano y una regla no graduada para trazar todas las figuras a partir de la recta o segmentos de recta y del círculo o arcos.
Los triángulos son figuras planas que resultan de unir 3 puntos con líneas rectas, y se clasifican según la longitud de sus lados y sus ángulos.
Las alturas de los triángulos son las rectas que pasan por uno de sus vértices y son perpendiculares al lado opuesto de dicho vértice, o a su prolongación.
En el triángulo acutángulo, el ortocentro se encuentra dentro del triángulo; en el triángulo rectángulo está donde se ubica el ángulo recto, y en el triángulo obtusángulo, en el exterior del triángulo.
El reto de hoy:
Consulta tu libro de texto de Matemáticas de tercer grado de secundaria para profundizar en el tema y encontrar algunos ejemplos para practicar.
Igualmente, manifiesta las dudas con tus maestros y maestras de Matemáticas, o consulta otras fuentes de apoyo para resolverlas.
¡Buen trabajo!
Gracias por tu esfuerzo.