Un subibaja matemático: proporcionalidad inversa
Un subibaja matemático: proporcionalidad inversa
Aprendizaje esperado: analiza y compara situaciones de variación lineal y proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica. Interpreta y resuelve problemas que se modelan con este tipo de variación, incluyendo fenómenos de la física y otros contextos.
Énfasis: analizar situaciones de proporcionalidad inversa a partir de sus representaciones tabular, gráfica y algebraica.
¿Qué vamos a aprender?
En esta sesión, profundizarás en la proporcionalidad inversa e identificarás sus principales características. Para ello, analizarás y resolverás problemas que se modelan con este tipo de variación a partir de sus representaciones algebraica, tabular y gráfica.
¿Qué hacemos?
Antes de comenzar, reflexiona en lo siguiente, ya que te servirá para la resolución de los problemas que se presentarán en esta sesión.
Si tuvieras que describir el movimiento de un carrito de juguete en línea recta, ¿qué aspectos considerarías?
Una descripción sencilla del movimiento del carrito sería que, en la velocidad interviene la distancia y el tiempo, por ejemplo.
Para profundizar en ello, considera algunos aspectos de la física. La velocidad media de un objeto es la razón o cociente de la distancia recorrida por el objeto entre el tiempo transcurrido. En lenguaje algebraico se dice que “v” es igual a “d” entre “t”
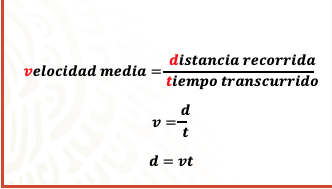
En donde despejando a “d”, se tiene que es igual a “v” por “t”.
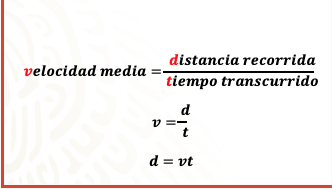
Pero ¿por qué despeja “d”? En este caso, la distancia está fija, mientras que la velocidad y el tiempo del carrito son variables. Para comprender esta relación, analiza la siguiente situación.
Situación-problema: carrito de juguete
Antonio juega con su carrito de juguete, lo lanza 4 veces hacía una pared que se ubica a “10 m” de distancia. La hermana de Antonio utiliza un cronómetro para registrar en una tabla el tiempo (t) que el carrito tarda en llegar a la pared en cada lanzamiento.
Obteniendo en el primer lanzamiento 5 segundos; en el segundo lanzamiento, 10 segundos; en el tercer lanzamiento, 3 segundos, y en el cuarto lanzamiento, 6 segundos.
¿Cuál es la velocidad (v) del objeto para cada tiempo (t)?

Al observar los datos de la tabla, se puede deducir que el carrito lleva velocidades distintas al recorrer la misma distancia.
Analiza el comportamiento de las variables tiempo (t) y velocidad (v) involucradas. Para ello, considera las siguientes preguntas:
- ¿Cuál es la velocidad (v) del objeto para cada tiempo (t)?
- ¿Cómo se comporta la velocidad (v) del carrito respecto al tiempo (t)?
- ¿Qué relación existe entre el tiempo (t) y la velocidad (v) correspondiente?
Ahora, analiza los datos calculando las velocidades correspondientes organizando el tiempo de menor a mayor.
Utiliza la fórmula: d = v t Sustituyendo el valor de “d” igual a 10 metros, se tiene que:
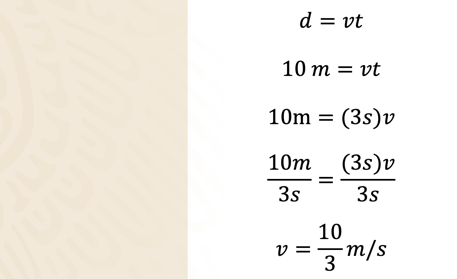
Ahora sustituye a “t” por 3 segundos, que es el menor tiempo que se obtuvo y realiza las operaciones correspondientes:
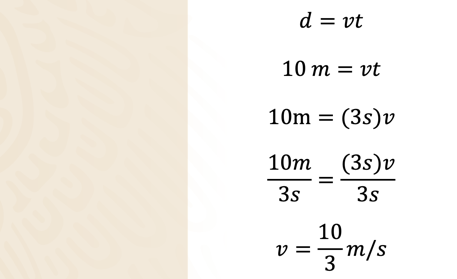
Por lo tanto, para calcular la velocidad correspondiente, los 10 metros se dividen entre el tiempo en segundos que tardó el carrito en el lanzamiento.
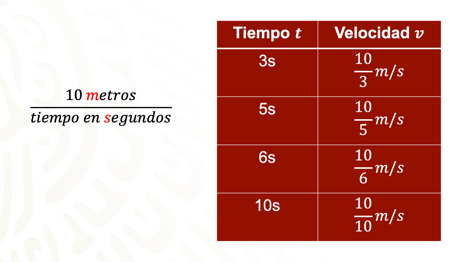
Con lo cual se puede completar el primer renglón de la siguiente tabla. En la primera columna están ordenados, de menor a mayor, los tiempos de cada lanzamiento.

De la misma manera que se realizó para el primer renglón, se pueden obtener el resto de las velocidades que faltan en la segunda columna, obteniendo 10 entre 5 metros sobre segundo en el segundo renglón, 10 entre 6 metros sobre segundo en el tercer renglón, y 10 entre 10 metros sobre segundo en el último lanzamiento. Con esto la tabla queda de la siguiente manera:
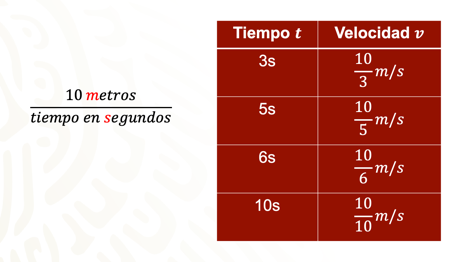
Ahora, analiza los datos obtenidos.
Observa el segundo y cuarto renglón, se tiene que el tiempo aumenta al doble mientras la velocidad media disminuye a la mitad.
El doble de 3 segundos es 6 segundos, por otro lado, la mitad de “10 tercios de metros sobre segundo”, es “10 sextos de metros sobre segundo”.
Pero ¿qué pasa con la velocidad si el tiempo aumenta al triple?
El tiempo dado es: t = 9 segundos, y se sabe que la velocidad se obtiene con la siguiente fórmula:

Sustituyendo el tiempo se obtiene la velocidad, 10 sobre 9 metros por segundo.

Observa que: 10 novenos es igual a un tercio por 10 tercios de metros sobre segundo. Es decir, la velocidad disminuye una tercera parte mientras el tiempo aumenta al triple.

Por lo tanto, se puede decir que conforme el tiempo aumenta, la velocidad disminuye en la misma proporción. Además, el producto entre el tiempo (t) y la velocidad (v) es igual a 10, la cual se llama constante de proporcionalidad inversa.
Pero ¿qué pasa con el tiempo si la velocidad aumenta al triple?
Piensa que la velocidad (v) es de 4 metros por segundo. Utilizando la fórmula: d = v t Entonces se tiene que:

Realizando las operaciones correspondientes, se tiene que “t” es igual a cinco medios que es igual a 2.5 segundos.


Comparando con la velocidad 1 m/s del penúltimo renglón, se identifica que una velocidad de 4 m/s es el cuádruple o 4 veces, mientras que el tiempo 2.5 segundos que se obtiene es la cuarta parte de 10 segundos.
A partir de los casos anteriores se puede decir que las variables “t” y “v” son inversamente proporcionales.
Continúa con otra situación de este tipo.
En la geometría también se presentan situaciones de proporcionalidad inversa, específicamente en el cálculo de áreas. Analiza el siguiente problema agrario.
Situación-problema: agrario
Un campesino ejidal quiere cercar un terreno rectangular de 120 metros cuadrados de superficie donde piensa cosechar maíz para cuidarlo del maíz transgénico
¿Cuáles son las dimensiones del terreno?
Para que puedes responder, apóyate de lo que ya sabes, es decir, el área de un rectángulo es igual a su base por su altura. Observa algunas posibles opciones de terrenos rectangulares:
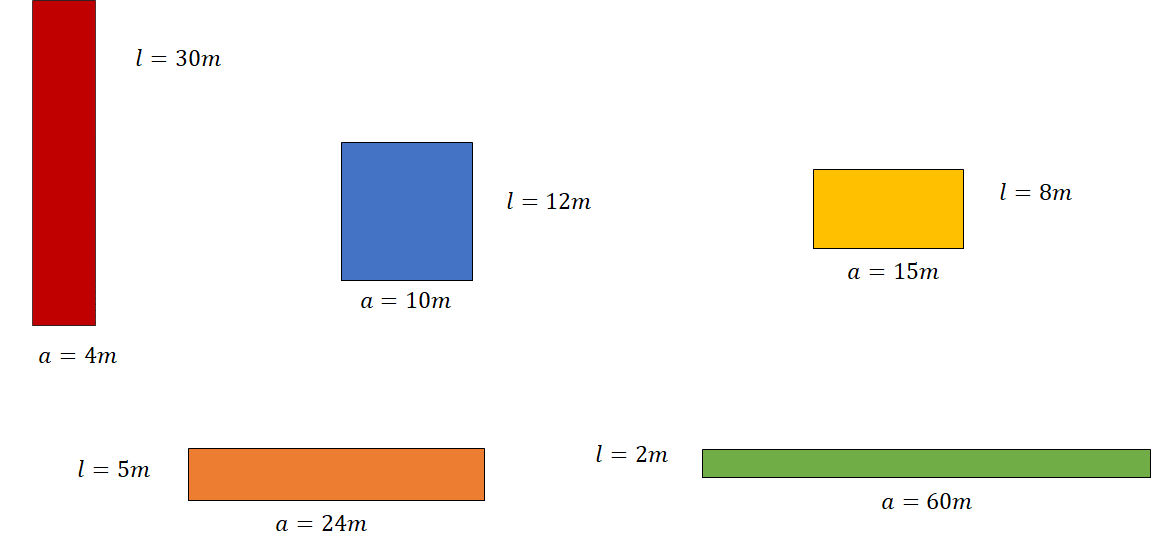
El terreno rojo tiene 4 metros de base y 30 metros de altura, mientras que el terreno azul mide 10 metros de base y 12 metros de altura, y así sucesivamente, sin olvidar que todos deben tener 120 metros cuadrados de área.
Considera que hay terrenos de distintos tamaños, unos más alargados, otros más anchos, algunos con forma de cuadrado, pero la clave está en que se pueda ordenar la información para identificar relaciones que a simple vista no son fáciles de percibir.
Para poder analizar mejor el comportamiento de las dimensiones de los rectángulos, organízalos como se muestra en el siguiente esquema.
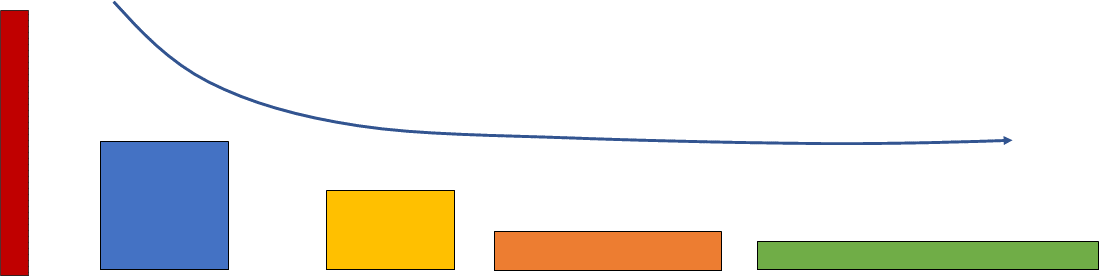
Ahora, se puede observar que las alturas de los rectángulos van disminuyendo conforme las bases aumentan, pero la pregunta clave es: ¿las alturas disminuyen mientras las bases aumentan en la misma proporción?
Para responder esta pregunta, elabora una tabla de datos con 4 columnas: en la primera colocarás el color del rectángulo; en la segunda, la longitud de las bases “b”; en la tercera columna, la longitud las alturas “a”; y al final el producto de ambas para confirmar que el rectángulo con dichas dimensiones tiene 120 metros cuadrados de superficie.
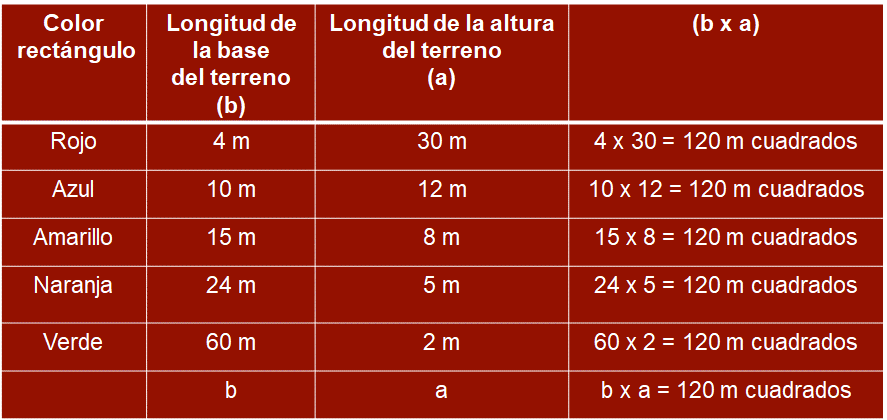
Los datos de cada rectángulo se ordenaron de manera creciente respecto a la base del terreno. El rectángulo rojo su base mide 4 metros y su altura es de 30 metros, mientras que en el rectángulo azul su base mide 10 metros y su altura es de 12 metros, y así sucesivamente hasta completar la tabla con los datos que se tienen. ¿Qué observas?
Existe un comportamiento similar de variación entre las magnitudes de la base y la altura de los rectángulos; por ejemplo, en el rectángulo rojo su base es la sexta parte de la base del rectángulo naranja, mientras que la altura del rectángulo rojo es seis veces la altura del rectángulo naranja.
Un comportamiento similar se tiene con las dimensiones del rectángulo amarillo y el rectángulo verde, mientras que la base del rectángulo amarillo es la cuarta parte de la base del rectángulo verde, la altura del rectángulo amarillo es cuatro veces la altura del verde.
Por ello, se puede decir que la base del terreno aumenta y la altura del terreno disminuye en la misma proporción, con constante de proporcionalidad igual a 120. Entonces, las magnitudes “b” y “a” son inversamente proporcionales.
Es momento de recapitular lo discutido hasta el momento.
Dos magnitudes “a” y “b” en proporción inversa:
- Su producto es constante “a” por “b” es igual a “k”
- Cuando una de ellas aumenta, la otra magnitud disminuye en la misma proporción.
- “k” es la constante de proporcionalidad.
Con ello, se puede plantear un problema inverso, es decir, partir de dos magnitudes que son inversamente proporcionales para calcular datos faltantes.
En los problemas anteriores lo que has hecho es partir de datos para inferir si la relación entre ellos es una proporción inversa. Ahora, la idea es aplicar lo discutido para encontrar valores faltantes en una relación de proporcionalidad inversa para ayudar en la toma de decisiones.
Analiza el siguiente problema.
Situación-problema: alimento de vacas
Un productor lechero tiene pasto y alimento procesado para mantener a 162 vacas durante 4 meses, pero sabe que habrá desabasto alimenticio en los próximos meses.
¿Cuántas vacas se podrán mantener en la finca durante 12 meses con el mismo alimento, si suponemos que todas las vacas comen la misma cantidad de alimentos?
Observa que la cantidad de alimento será la misma, es constante, lo que va a aumentar es el tiempo, entonces es de esperar que el número de vacas que se pueden alimentar sea menor, suponiendo que las condiciones son las mismas siempre. Por lo tanto, el tiempo “t” y el número de vacas “v” será inversamente proporcional.
Para iniciar con la resolución de este problema, elabora una tabla con los siguientes datos: una columna para el tiempo y otra para el número de vacas; en donde para el tiempo de 4 meses corresponden 162 vacas y para el tiempo de 12 meses corresponde un valor faltante de vacas “v” que se debe calcular.

Por las características de una proporción inversa, se sabe que los productos de los elementos en cada renglón son iguales a la constante de proporción. Entonces:
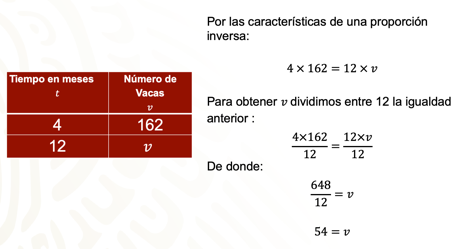
Para obtener “v”, se divide entre 12 la igualdad anterior:
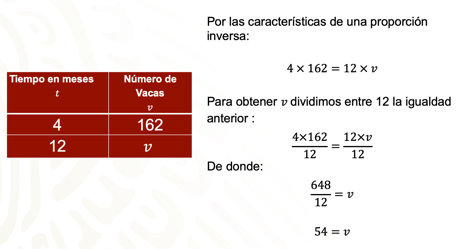
Realizando la división de 648 entre 12 se tiene que 54 es igual a “v”. Es decir, el número de vacas que podrá alimentar el granjero son 54
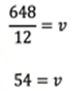
Con dicho dato el granjero ya tomará una decisión sobre si va a tener que vender algunas de sus vacas o trasladarlas a otra granja, lo que mejor le convenga.
¿Ya identificaste cómo las proporciones inversas pudieron ayudar a tomar decisiones? Las matemáticas pueden llegar a ser divertidas e interesantes, aunque hay que tener cuidado sobre cuándo concluir que dos variables o magnitudes son inversamente proporcionales.
Analiza la siguiente situación.
Situación-problema: terreno rectangular
El campesino ejidal ahora quiere cercar un terreno rectangular con 120 metros de malla. ¿Cuáles pueden ser las dimensiones del terreno?
Para resolver este problema, primero trabajarás con el perímetro del rectángulo, ya que se quiere cercar el terreno, a diferencia del problema anterior donde el campesino tenía un problema referente al área.
Observa algunos posibles tamaños del rectángulo que el campesino puede cercar.
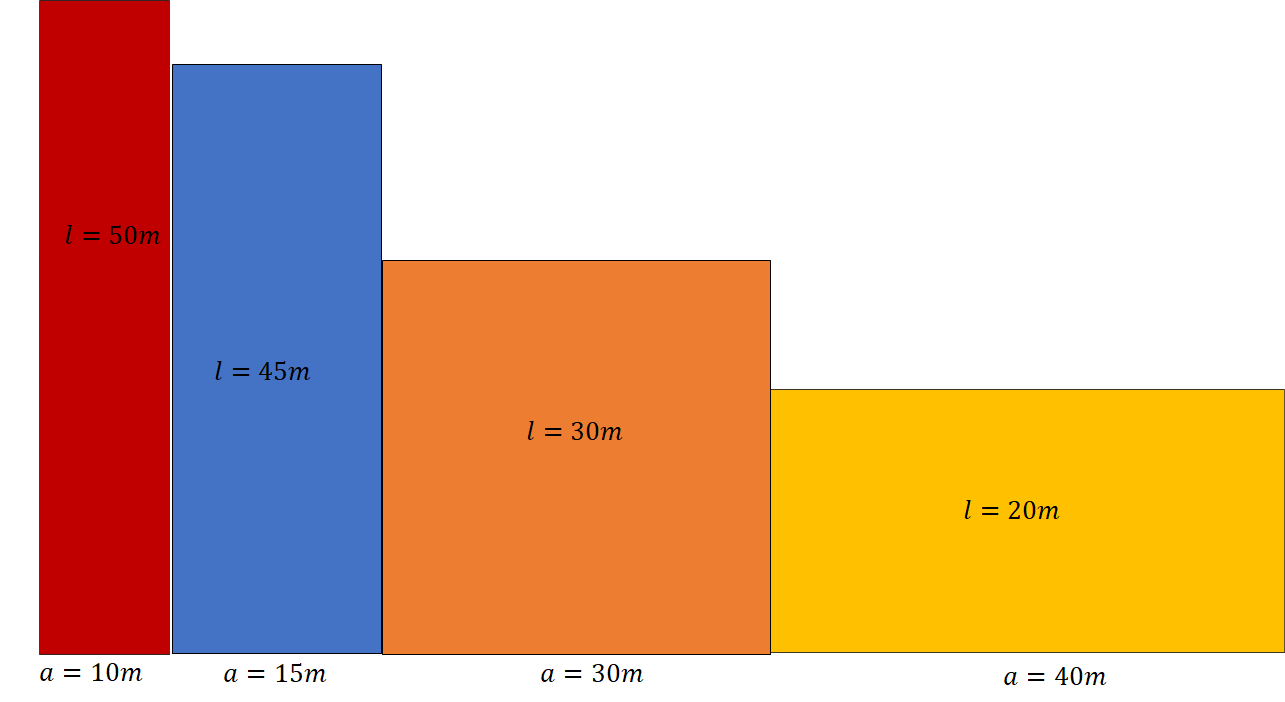
Una opción puede ser el rectángulo rojo de 10 metros de ancho y 50 metros de largo, como cada lado se repite en la figura, se tiene que su perímetro es igual a dos veces 10 más dos veces 50, lo cual da 120 metros. Otra opción puede ser el rectángulo azul que mide 15 metros de ancho y 45 metros de largo, también el rectángulo naranja de ancho y largo iguales a 30 metros, y el rectángulo amarillo 40 metros de ancho y 20 metros de largo. A primera vista se puede pensar que es un problema de variables inversamente proporcionales.
Ahora, elabora una tabla donde organices los datos de las posibles opciones para el ancho “a” y el largo “l” del terreno: en la primera columna colocarás el color del rectángulo; en la segunda columna, la longitud de su ancho; en la tercera columna, la longitud de su largo; y al final se calcula el perímetro para verificar que se obtienen los 120 metros de malla.
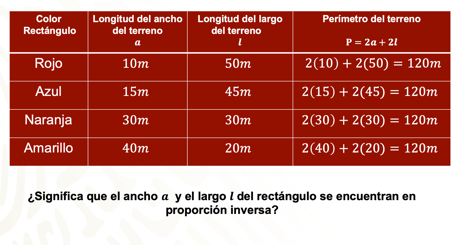
En el primer renglón, para el rectángulo rojo su ancho “a” es de 10 metros, mientras que su largo “l” es de 50 metros. Se realizan las operaciones correspondientes y se verifica que el resultado es 120 metros. Y así sucesivamente para el resto de los rectángulos.
Ahora, observa con detenimiento la tabla. Se nota que el ancho y el largo del rectángulo se comportan de tal manera que conforme uno aumenta el otro disminuye, ¿significa que el ancho “a” y el largo “l” del rectángulo se encuentran en proporción inversa?
Recuerda que una condición que deben satisfacer “a” y “l” consiste en que, su producto en cada renglón debe ser constante para reconocer la constante de proporcionalidad.
Para comprobarlo, elabora una tabla como la siguiente, donde en la última columna se encuentran los productos correspondientes a cada renglón:
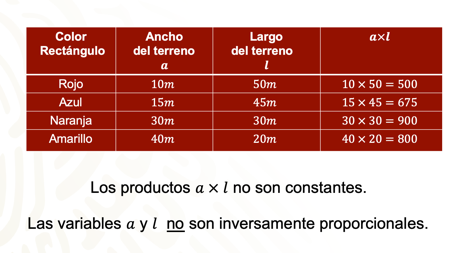
Analizando, los productos “a” por “l” de esta tabla no son constantes. Por ello las variables “a” y “l” no son inversamente proporcionales.
A primera vista uno podría suponer que las magnitudes de los lados del rectángulo en este caso también eran inversamente proporcionales, ya que tienen el comportamiento de un subibaja, mientras una aumenta, la otra disminuye.
Por ello, debes analizar el comportamiento de las variables, ya que la condición de que sus productos sean constantes no se satisface. Aunque una de las variables aumenta y la otra disminuye, no lo hacen en la misma proporción, ya que, si observas el segundo y tercer renglón, el ancho “a” del rectángulo aumenta al doble, mientras que el largo “l” no disminuye a la mitad, es decir, “a” aumenta y “l” disminuye, pero no en la misma proporción. Entonces, se puede decir que, el ancho “a” y el largo “l” del rectángulo no son inversamente proporcionales.
Aunque el comportamiento de dos variables o magnitudes sea que una crece mientras la otra decrece, eso no es suficiente para decir que dos variables son inversamente proporcionales.
Las características que debe cumplir una proporción inversa siempre deben verificar que los productos, entre ellas las variables, sean igual a una constante o, en otras palabras, mientras una variable crece, la otra decrece en la misma proporción y viceversa.
Has finalizado esta sesión. Recuerda que este es un material de apoyo y puedes consultar otras fuentes para complementar lo que aprendas aquí, como tu libro de texto de Matemáticas.
El reto de hoy:
Analiza y responde las siguientes preguntas.
En una proporción inversa:
¿Existen cantidades inversamente proporcionales cuya constante de proporcionalidad pueda ser negativa?
¿Qué signos deben tener las cantidades consideradas para que su constante de proporcionalidad sea una constante negativa?
Reflexiona y considera algún caso práctico donde se opere con cantidades con signos distintos.
¡Buen trabajo!
Gracias por tu esfuerzo.
Para saber más:
Lecturas